Keywords

1 Introduction

Spline interpolation belongs to the common challenges of numerical mathematics due to its application in many fields of computer science such as graphics, CAD applications or data modelling, therefore designing fast algorithms for their computation is an essential task. The paper is devoted to effective computation of bicubic spline derivatives using tridiagonal systems to construct interpolating spline surfaces. The presented reduced algorithm for computation of spline derivatives over non-uniform grids at the adjacent segment is based on the recently published approach for uniform spline surfaces [4,5,6], and it is faster than the de Boor’s algorithm [2].

The structure of this article is as follows. Section 2 is devoted to a problem statement. Section 3 briefly reminds some aspects of de Boor’s algorithm for computation of spline derivatives. To be self contained, de Boor’s algorithm is provided in Appendix and will be further referred to as the full algorithm. Section 4 presents the new reduced algorithm and the proof of its numerical equality to the full algorithm. The fifth section analyses some details for optimal implementation of both algorithms and provides measurements of actual speed increase of the new approach.

2 Problem Statement

This section defines inputs for the spline surface and requirements, based on which it can be constructed.

For integers \(I, J > 1\) consider a non-uniform grid

$$\begin{aligned}{}[x_0, x_1, \dots , x_{I-1}] \times [y_0, y_1, \dots , y_{J-1}], \end{aligned}$$
(1)

where

$$\begin{aligned} \begin{aligned} x_{i-1}< x_{i},&\quad i = 1, 2, \dots , I-1\text {,} \\ y_{j-1} < y_{j},&\quad j = 1, 2, \dots , J-1\text {.} \end{aligned} \end{aligned}$$
(2)

According to [2], a spline surface is defined by given values

$$\begin{aligned} z_{i,j}, \quad i = 0, 1, \dots , I-1, \quad j = 0, 1, \dots , J-1 \end{aligned}$$
(3)

at the grid-points, and given first directional derivatives

$$\begin{aligned} d^x_{i,j}, \quad i = 0, I-1, \quad j = 0, 1, \dots , J-1 \end{aligned}$$
(4)

at the boundary verticals,

$$\begin{aligned} d^y_{i,j}, \quad i = 0, 1, \dots , I-1, \quad j = 0, J-1 \end{aligned}$$
(5)

at the boundary horizontals and cross derivatives

$$\begin{aligned} d^{x,y}_{i,j}, \quad i = 0, I-1, \quad j = 0, J-1 \end{aligned}$$
(6)

at the four corners of the grid.

The task is to define a quadruple \([z_{i,j}, d^x_{i,j}, d^y_{i,j}, d^{x,y}_{i,j}]\) at every grid-point \([x_i, y_j]\), based on which a bicubic clamped spline surface S of class \(C^2\) can be constructed with properties

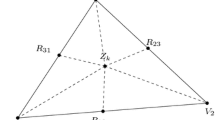
$$\begin{aligned} \begin{aligned} S(x_i, y_j)&=z_{i,j},\\ \frac{\partial S(x_i,y_j)}{\partial x}&=d^x_{i,j}, \end{aligned} \qquad \begin{aligned} \frac{\partial S(x_i,y_j)}{\partial y}&=d^y_{i,j}, \\ \frac{\partial ^2 S(x_i,y_j)}{\partial x \partial y}&=d^{x,y}_{i,j}. \end{aligned} \end{aligned}$$

For \(I = J = 3\) the input situation is illustrated in Fig. 1 below where bold marked values represents (3)–(6) while the remaining non-bold values represent the unknown derivatives to compute.

Fig. 1.
figure 1

Input situation for \(I,J = 2\).

Full size image

3 Full Algorithm

The section provides a brief summary of the full algorithm designed by de Boor for computing the unknown first order derivatives that are necessary to compute a \(C^2\) class spline surface over the input grid.

For the sake of readability and simplicity of the model equations and algorithms we introduce the following notation.

Notation 1

For \(k \in \mathbb {N}^0\) and \(n \in \mathbb {N}^+\) let \(\{h_k\}_{k = 0}^n\) be an ordered list of real numbers. Then the value is defined as

(7)

where \(h_k \in \{x_k, y_k\}\).

The full algorithm is based on a model Eq. (8) that contains indices \(k = 0, 1, 2\) and parameters \(d_k\), \(p_k\) and \(h_k\). This model equation is used to construct different types of equation systems with corresponding indices and parameters.

Let us explain how a model equation can be used to compute first order derivatives with respect to x in the simplest case of a \(j^{\text {th}}\) row over a \(3\times 3\) sized input grid (1) with given values (3)–(6). The input situation is graphically displayed in Fig. 1. To calculate the single unknown \(d^x_{1,j}\), substitute the values \((h_0, h_1, h_2)\) with \((x_0, x_1, x_2)\), \((p_0, p_1, p_2)\) with \((z_{0,j}, z_{1,j}, z_{2,j})\) and \((d_0, d_1, d_2)\) with \((d^x_{0,j}, d^x_{1,j}, d^x_{2,j})\) in (3), (4). Then \(d_1 = d^x_{1,j}\) can be calculated using the following model equation, where D stands for derivatives and P for right-hand side parameters,

(8)

where

(9)

and

(10)

The final algorithm for all rows and columns of any size can be found in Appendix.

4 Reduced Algorithm

The reduced algorithm for uniform splines is originally proposed by this article’s second author, see also [6, 8]. The model equation was obtained thanks to a special approximation property between biquartic and bicubic polynomials. The resulting algorithm is similar to the de Boor’s approach, however the systems of equations are half the size and compute only half of the unknown derivates, while the remaining unknowns are computed using simple remainder formulas.

In the reduced algorithm for uniform grids the total number of arithmetic operations is equal or larger than in the full algorithm. However the algorithm is still faster than the full one thanks to two facts Firstly, it contains fewer costly floating point divisions. The second reason is that the form of the reduced equations and rest formulas is more favourable to some aspects of modern CPU architectures, namely the instruction level parallelism and system of the relatively small fast hardware caches as described in [4].

The way used to derive the new model equations can be easily generalized from uniform to non-uniform grids, however in latter case the equations are more complex and even contain more arithmetic operations than the full equations. Thus it was not clear whether the non-uniform reduced equations would be more efficient. The numerical experiments showed that the instruction level parallelism features of modern CPUs are able to mitigate the higher complexity of reduced equations and therefore imply slightly lower execution time also for non-uniform grids.

The reduced algorithm is based on two different model equations, a main and an auxiliary one, and on an explicit formula. Let us explain how the main model equation can be used to compute derivatives for the simplest case of a \(j^{\text {th}}\) row over a \(5\times 5\) sized grid. By analogy to the previous section, substitute the values \((h_0, \dots , h_4)\) with \((x_0, \dots , x_4)\), \((p_0, \dots , p_4)\) with \((z_{0,j}, \dots , z_{4,j})\) and \((d_0, \dots , d_4)\) with \((d^x_{0,j}, \dots , d^x_{4,j})\). For the row j of size 5 there are three unknown values \(d_1, d_2\) and \(d_3\). First, calculate \(d_2 = d^x_{2,j}\) using the following model equation

(11)

where

(12)

and

(13)

Then the unknown \(d_1\) can be calculated from

(14)

where

(15)

Relation (14) will be referred to as the explicit rest formula and it is also used to compute the unknown value with different indices of the right-hand side parameters.

In case the j-th row contains only four nodes, the model Eq. (11) should be replaced with the auxiliary model equation for even-sized input rows or columns

(16)

where

(17)

and

(18)

Thus the reduced algorithm comprises the equation system constructed from two model Eqs. (11), (16) to compute even-indexed derivatives and the rest formula (14) to compute the odd-indexed derivatives.

The reduced algorithm for arbitrary sized input grid also consists of four main steps, similarly to the full algorithm, each evaluating equation systems constructed from the main (11) and auxiliary (16) model equations, and it is summarized by the lemma below.

Lemma 1

(Reduced algorithm). Let the grid parameters \(I, J > 2\) and the x, y, z values and d derivatives be given by (1)–(6). Then the values

$$\begin{aligned} \begin{aligned} d^x_{i,j},&\quad i = 1, \dots , I-2, \quad j = 0, \dots , J-1,\\ d^y_{i,j},&\quad i = 0, \dots , I-1, \quad j = 1, \dots , J-2,\\ d^{x,y}_{i,j},&\quad i = 0, \dots , I-1, \quad j = 0, \dots , J-1 \end{aligned} \end{aligned}$$
(19)

are uniquely determined by the following \(\frac{3I+2J+5}{2}\) linear systems of altogether \(\frac{5IJ-I-J-23}{4}\) equations and \(\frac{7IJ-7I-7J+7}{4}\) rest formulas:

for each \(j = 0, 1, \dots ,J-2\),

(20)

for each \(i = 1, 3, \dots , I-2\) and \(j = 1, 3, \dots , J-2\),

(21)

for each \(i = 0, 1, \dots ,I-1\),

(22)

for each \(j = 1, 3, \dots , J-2\) and \(i = 1, 3, \dots , I-2\),

(23)

for each \(j = 0, J-1,\)

(24)

for each \(i = 1, 3, \dots , I-2\) and \(j = 1, 3, \dots , J-2\),

(25)

for each \(i = 0, 1, \dots ,I-1\),

(26)

for each \(j = 1, 3, \dots , J-2\) and \(i = 1, 3, \dots , I-2\),

(27)

If I is odd, then the last model equation in steps (20) and (24) needs to be accordingly replaced by auxiliary model Eq. (16). Analogically, if J is odd, the same applies to steps (22) and (26).

Before the actual proof we should note that the reduced algorithm is intended as a faster drop-in replacement for the classic full algorithm. Therefore it should be equivalent to the full algorithm as well as to reach lower execution time to be worth of actual implementation.

Proof

To prove the equivalence of the reduced and the full algorithm we have to show that the former implies the latter.

Consider values and derivatives from (1)–(6) for \(I,J = 5\). For the sake of simplicity consider only the \(j^{\text {th}}\) row of the grid and substitute values \((h_0, \dots , h_4)\) with \((x_0, \dots , x_4)\), \((p_0, \dots , p_4)\) with \((z_{0,j}, \dots , z_{4,j})\) and \((d_0, \dots , d_4)\) with \((d^x_{0,j}, \dots , d^x_{4,j})\).

The unknowns \(d_1 = d^x_{1,j}, ..., d_3 = d^x_{3,j}\) can be computed by solving the full tridiagonal system (30) of size 3. We have to show that the reduced system (20) with corresponding rest formula (21) is equivalent to the full system of size 3. One can easily notice that (20) consists of only one equation and (21) consists of two rest formulas.

The rest formula with \(k = 1, 3\)

can be easily modified into

thus giving us the first and the last equations of the full equation system of size 3. The second equation of the full equation system of size 3 can be obtained from the reduced model Eq. (11). From rest formulas

we express

Then substitute and for \(d_0\) and \(d_4\) in the reduced model equation

thus we get the second equation of the full system.

Analogically, this proof of equivalence can be extended for any number of rows or columns as well as for the case of even sized grid dimensions I and J that use the auxiliary model Eq. (16).    \(\square \)

5 Speed Comparison

The reduced algorithm is numerically equivalent to the full one, however there is still a question of its computational effectiveness.

First of all, let’s discuss the implementation details of both algorithms and propose some low level and rather easy optimizations that significantly decrease the execution time. These optimizations positively affect both algorithms, but the reduced one is influenced to a greater extent. Although, it must be mentioned that the reduced algorithm is faster even without the optimization.

5.1 Implementation Details

The base task of both algorithms is computation of the tridiagonal system of equations described in (30), (31), (32) and (33) for the full algorithm and (20), (22), (24) and (26) for the reduced algorithm. It can be easily proved that the reduced systems are diagonally dominant, therefore our reference implementation uses the LU factorization as the basis for both full and reduced algorithms.

There are several options to optimize the equations and formulas used in both algorithms. One option is to modify the model equations to lessen the number of slow division operations, since the double precision floating point division is 3–5 times slower than multiplication, see the CPU instructions documentation [3, 9, 10]. This will measurably decrease the evaluation time of both algorithms.

Another, more effective optimization is memoization. Consider the full equation system from (30). The equations can be expressed in the form of

$$\begin{aligned} \begin{aligned}&l_2 \cdot d_2 + l_1 \cdot d_1 + l_0 \cdot d_0 = r_2 \cdot p_2 + r_1 \cdot p_1 + r_0 \cdot p_0\text {} \end{aligned} \end{aligned}$$
(28)

where \(l_{i-1}\), \(l_{i}\), \(l_{i+1}\), \(r_{i-1}\), \(r_{i}\) and \(r_{i+1}\) depend on and/or . Since most of the values are used more than once in the equation system, these can be precomputed to simplify the equations and to reduce the number of calculations. Analogically, such optimization can be performed for each of the full equation systems and, of course, for each of the reduced equation systems and rest formulas as well, where such simplification will be more beneficial as the model expressions for reduced algorithm (11), (16) and (14) are more complex than those in the full algorithm (8). In our implementation for benchmarking of both algorithms, we consider only optimized equations.

Computational Complexity. We should give some words about importance of the suggested optimization. For I, J being dimensions of an input grid, the total arithmetic operation count of the full algorithm is asymptotically 63IJ of which 12IJ are divisions. For the reduced algorithm the count is 129IJ where the number of divisions is the same. These numbers of operations takes into account the model equations and a LU factorization of equation systems.

Given these numbers it may be questionable if the reduced algorithm is actually faster than the full one. However thanks to the pipelined superscalar nature of the modern CPU architectures and general availability of auto-optimizing compilers, the reduced algorithm is still approximately 15% faster than the full one depending on the size of grid.

For implementations with optimized form of expressions and memoization, the asymptotic number of operations is 33IJ of which 3IJ are divisions for the full algorithm. For the reduced algorithm the count is significantly lessened to 30IJ where the number of divisions is only 1.5IJ. While the optimized full algorithm is only slightly faster than the unoptimized one, in case of the reduced algorithm the improvements are more noticeable. Comparing such implementations, the reduced algorithm is up to 50% faster than the optimized full algorithm. More detailed comparison of the optimized implementations is in following Subsect. 5.2.

Memory Requirements. For the sake of completness a word about memory requirements and data structures used to store input grid and helper computation buffers should be given.

To store the input grid one needs \(I+J\) space to store x and y coordinates of the total \(I\cdot J\) grid nodes, and additional 4IJ space to store the z, \(d^x\), \(d^y\) and \(d^{xy}\) values for each node, thus giving us overall \(4IJ + I + J\) space requirement just to store the input values.

Needs of the full and reduced algorithms are quite low considering the size of the input grid. The full tridiagonal systems of Eqs. (30)–(33) needs \(5\cdot max(I, J)\) space to store the lower, main and upper diagonals, right-hand side and an auxiliary buffer vector for the LU factorization. If the memoization technique described above is used, then there is a need for another \(3I+3J\) auxiliary vectors for precomputed right-hand side attributes, thus the total memory requirement for the computationally optimized implementation is \(5\cdot max(I, J) + 3(I + J)\) of space.

The reduced algorithm needs \(\frac{5}{2} \cdot max(I, J)\) of space for the non-memoized implementation. Using a memoization optimization the reduced algorithm requires additional \(\frac{5}{2}(I+J)\) to store precomputed right-hand side attributes of the equation systems and rest formulas, thus giving us \(\frac{5}{2} \cdot (max(I, J) + I+J)\) space needed to store computational data, that is less than the space requirement of the full algorithm.

Mention must be made that the speedup for uniform grid was achieved without special care for memoization that here play a significant role.

Data Structures. Consider the input situation (1)–(6) from Sect. 2. Since the input grid may contain tens of thousands or more nodes the most effective representation of the input grid is a jagged array structure for each of the \(z_{i,j}\), \(d^x_{i,j}\), \(d^y_{i,j}\) and \(d^{xy}_{i,j}\) values. Each tridiagonal system from either of the two algorithms always depends on one row of the jagged array, thus during equation system evaluation the entire subarrays of the jagged structure can be effectively cached, supposed that the I or J dimension is not very large, see Table 1. Notice that the iterations have interchanged indices i, j in (30), (20) and (21) compared to the iteration in (31), (33), (22), (23), (26) and (27). For optimal performance an effective implementation should setup the jagged arrays in accordance with how we want to iterate the data [7].

5.2 Measured Speedup

Now it is time to compare optimal implementations of both algorithms taking into account the proposed optimizations in the previous subsection.

For this purpose a benchmark was implemented in and compiled with a 64 bit GCC 7.2.0 using -Ofast optimization level and individual native code generation for each tested CPU using -march=native setting. Testing environments comprised several computers with various recent CPUs where each system had 8–32 GB of RAM and Windows 10 operating system installed. The tests were conducted on freshly booted PCs after 5 min of idle time without running any non-essential services or processes like browsers, database engines, etc.

The tested data set comprised the grid \([x_{0}, x_{1}, \dots , x_{I}] \times [y_{0}, y_{1}, \dots , y_{J}]\) where \(x_{0} = -20\), \(x_{I} = 20\), \(y_{0} = -20\), \(y_{J} = 20\) and values \(z_{i,j}\), \(d^x_{i,j}\), \(d^y_{i,j}\), \(d^{x,y}_{i,j}\), see (3)–(6), are given from function \(sin \sqrt{x^2+y^2}\) at each grid-point. Concrete grid dimensions I and J are specified in Tables 1 and 2. The speedup values were gained averaging 5000 measurements of each algorithm.

Table 1 represents measurements on five different CPUs and consists of seven columns. The first column contains the tested CPUs ordered by their release date. Columns two through four contain measured execution times in microseconds for both algorithms and their speed ratios for grid dimension \(100\times 100\), while the last three columns analogically consist of times and ratios for grid dimension \(1000\times 1000\).

Table 1. Multiple CPU comparison of full and reduced algorithms tested on two datasets. Times are in microseconds.
Full size table

Table 2, unlike the former table, represents measurements on different sized grids. For the sake of readability the table contains measurements from single CPU.

Let us summarize the measured performance improvement of the reduced algorithm in comparison with the full one. According to Tables 1 and 2 the measured decrease of execution time for small grids of size smaller than \(500 \times 500\) is approximately \(50\%\) while for the datasets of size \(1000 \times 1000\) or larger the average speedup drops to \(30\%\). A noteworthy fact is, that the measured speed ratio between the full and reduced algorithms is in line for grids with dimensions in the order of hundreds where the total number of spline nodes will be in the order of tens of thousands. In other words the individual rows or columns of the grid should fit in the CPUs’ L1 cache. In case of a sufficiently large grid, the caching will be less effective resulting in a much costlier read latency eventually mitigating the speed-up of the reduced algorithm. At some point, for very large datasets, the algorithms will be memory bound and therefore performing similarly.

Table 2. Multiple dataset comparison of full and reduced algorithms tested on i7 6700K. Times are in microseconds.
Full size table

6 Discussion

Let us discuss the new algorithm from the numerical and experimental point of view. The reduced algorithm works with two model equations and a simple formula, see (11), (16) and (14). The reduced tridiagonal equation systems (20), (22), (24), (26) created from model Eqs. (11), (16) contain only two times less equations than the corresponding full systems. In addition, the reduced systems are diagonally dominant and therefore, from the theoretical point of view, computationally stable [1], similarly to the full systems. The other half of the unknowns are computed from simple explicit formulas, see (21), (23), (25), (27), and therefore do not present any issue. The maximal numerical difference between the full and reduced system solutions during our experimental calculations in our  implementation was shown to be in the order of \(10^{-16}\). As this computational error is precision-wise the edge of FP64 numbers of the IEEE 754 standard we can conclude that the proposed reduced method yields numerically accurate results in a shorter time.

7 Conclusion

The paper introduced a new algorithm to compute the unknown derivatives used for bicubic spline surfaces of class \(C^2\). The algorithm reduces the size of the equation systems by half and computes the remaining unknown derivatives using simple explicit formulas. A substantial decrease of execution time of derivatives at grid-points has been achieved with lower memory space requirements at the cost of a slightly more complex implementation. Since the algorithm consist of many independent systems of linear equations, it can be also effectively parallelized for both CPU and GPU architectures.