Differential Cryptanalysis of Round-Reduced Sparx-64/128

Abstract

Sparx is a family of ARX-based block ciphers designed according to the long-trail strategy (LTS) that were both introduced by Dinu et al. at ASIACRYPT’16. Similar to the wide-trail strategy, the LTS allows provable upper bounds on the length of differential characteristics and linear paths. Thus, the cipher is a highly interesting target for third-party cryptanalysis. However, the only third-party cryptanalysis on Sparx-64/128 to date was given by Abdelkhalek et al. at AFRICACRYPT’17 who proposed impossible-differential attacks on 15 and 16 (out of 24) rounds.

In this paper, we present chosen-ciphertext differential attacks on 16 rounds of Sparx-64/128. First, we show a truncated-differential analysis that requires $2^{32}$ chosen ciphertexts and approximately $2^{93}$ encryptions. Second, we illustrate the effectiveness of boomerangs on Sparx by a rectangle attack that requires approximately $2^{59.6}$ chosen ciphertexts and about $2^{122.2}$ encryption equivalents. Finally, we also considered a yoyo attack on 16 rounds that, however, requires the full codebook and approximately $2^{126}$ encryption equivalents.

R. Ankele—This research was partially supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. H2020-MSCA-ITN-2014-643161 ECRYPT-NET.

1 Introduction

ARX Ciphers. The design and cryptanalysis of block ciphers is a heuristic competition between designers and analysts. With the introduction of the wide- trail design strategy in Rijndael, designers could finally provide provable bounds for the expected probabilities and therefore for the maximal length of differential characteristics and linear trails of block ciphers. Rijndael and similar designs are substitution-permutation networks (SPNs), which left the earlier path of using only the omnipresent modular addition, XOR, rotation, and shift operations that most processors support out-of-the-box. Thus, SPNs demand an expertised tailoring of their implementations to the operating platform to be comparably efficient as bit-based designs. However, in resource-constrained environments, the most efficient software implementations are still ciphers that employ only logical operations and/or addition, e.g., ciphers based on modular additions, rotations, and XOR (ARX). Hence, until recently, there has been a gap between the provable bounds of wide-trail designs, and the efficiency of ARX-based constructions.

Sparx. At ASIACRYPT’16, Dinu et al. introduced Sparx [7], the first ARX-based family of block ciphers that provides provable bounds on the maximal length of differential characteristics and linear trails. Alongside Sparx, the authors developed the long-trail design strategy, a general approach for ARX-based symmetric-key primitives to obtain provable bounds. Both the long-trail strategy in general, and Sparx in particular, are interesting targets of cryptanalysis as they try to bridge the gap between efficiency and providing security bounds. The question arises if it is also secure against (truncated) differential and boomerang attacks that can exploit clustering effects of many differential characteristics.

Research Gap and Related Work. In the specification of Sparx, the designers reported on their results of a first automated analysis that no differential characteristic with probability higher than $2^{-n}$ nor any linear characteristic with bias higher than $2^{-n/2}$ exists over five or more steps. Moreover, they described integral attacks on up to five out of eight steps of Sparx-64/128, and six out of ten steps of Sparx-128. Though, those initial attacks are naturally limited due to time constraints when designing a new cipher, and therefore demand a deeper analysis by the cryptographic community. At AFRICACRYPT’17, Abdelkhalek et al. [1] proposed 12- and 13-round impossible-differential distinguishers on Sparx-64/128, using the four-step distinguisher for balanced Type-1 Feistel networks. They extended their attacks by three rounds, respectively, where they exploited dependencies between the key words from the key-schedule. Recently, Tolba et. al. proposed multi-dimensional zero-correlation linear attacks on up to 26 rounds of Sparx-128/128, and on up to 29 rounds of Sparx-128/256 [13].

Table 1. Previous and proposed attacks on Sparx-64/128. KP/CP/CC = known plaintext/chosen plaintext/chosen ciphertext. ID = Impossible differential, TD = Truncated differentials.

Contribution and Outline. This work adds two chosen-ciphertext attacks on Sparx-64/128 in the single-key model: (1) a truncated-differential attack on 16 rounds and (2) a rectangle attack on 16 rounds; moreover, we further considered yoyo attacks on the same number of rounds, which, however, requires the full codebook. Due to space constraints, that attacks will be available in a full version alongside this work [2]. Table 1 compares their parameters with the previous attacks on Sparx-64/128 from the literature. In the remainder, we briefly revisit the necessary notions as well as the details of Sparx-64 in Sect. 2. We describe our truncated-differential attack in Sect. 5. We continue with an informal introduction to boomerang and rectangle attacks in Sect. 3. In Sect. 4, we describe our search of differential trails before we detail our rectangle attack on Sparx-64/128 in Sect. 6. Finally, Sect. 7 concludes this work.

2 Preliminaries

General Notations. We denote by $\mathbb {F} _2^{}$ the finite field of two elements $x \in \{0,1\}$. For positive integer n, we denote by $\mathbb {F} _2^{n}$ the space of n-element vectors from $\mathbb {F} _2^{}$. We represent functions by upper case letters and indices by lowercase letters. $\{0,1\}^{n}$ is the set of all n-bit strings and $\{0,1\}^{*}$ the set of bit strings of arbitrary length. Let $x, y \in \{0,1\}^{n}$ for some positive integer n in the following. Then, we denote by $x \,\Vert \, y$ the concatenation of x and y, by $x \oplus y$ their bitwise XOR, by $x \lll r$ a rotation by r bit to the left and by $x \ggg r$ rotation by r bit to the right; moreover, we denote by $x\,\boxplus \,y = (x\,+\,y) \bmod 2^n$ modular addition, and by $x \boxminus y = (x\,-\,y) \bmod 2^n$ modular subtraction. For all bit strings $x \in \{0,1\}^{n}$, we index the bits $x = (x_{n-1} \ldots x_1x_0)$ where $x_{n-1}$ is the most significant and $x_0$ the least significant bit of x. Given a bit string $x = (x^1 \,\Vert \, \ldots \,\Vert \, x^m) \in (\{0,1\}^{mn})$ consisting of m words of n bit each, we denote by

$$\begin{aligned} x \lll _n r {\mathop {=}\limits ^{\text {def}}} (x^1 \lll r) \,\Vert \, \ldots \,\Vert \, (x^m \lll r) \end{aligned}$$

the word-wise independent rotated value. We overload the notation for tuples of bit strings $x \in (\{0,1\}^{n})^m$: $x = (x^1, \ldots , x^m)$, to still mean wordwise independent rotation $x \lll _n r {\mathop {=}\limits ^{\text {def}}} (x^1 \lll r), \ldots , (x^m \lll r)$. We use typewriter font to represent hexadecimal values, e.g., $\texttt {0110} = 272$. We use the same font but with annotation to represent bit strings, e.g., $(\texttt {0110})_2 = 6$; moreover, we will use the symbol $\texttt {*}$ at the position of that certain bits to indicate that they can take arbitrary values, e.g., $(\texttt {0\,*\,10})_2 \in \{2, 6\}$. As a shorthand notation for probabilities p, we often write $h_w = -\log _2(p)$ when the meaning of p is clear from the context.

2.1 The Sparx Family of Ciphers

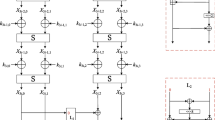
The Sparx-n/k family comprises three versions, Sparx-64/128, Sparx-128/128, and Sparx-128/256, where n indicates the block size, and k the key length k. The cipher is based on a Feistel network with two state words for Sparx-64 and four state words for Sparx-128, consisting of $n_s$ Feistel steps. Each step consists of $r_a$ rounds of an ARX-based round function; plain- and ciphertexts consist of $w = n/32$ words $X^{0}, \ldots , X^{w-1}$ of 32 bit each; the key is divided into 32-bit words $(\kappa ^0, \ldots , \kappa ^{v-1})$. The values for the individual versions of Sparx are summarized in Table 2, the components of the cipher are also depicted in Fig. 1.

Fig. 1.

High-level view of Sparx-64. Top left: The step function. Top center: The $\mathcal {A} ^3$ layer in Sparx-64. Top right: The linear layer $\mathcal {L}$. Bottom left: The $\mathcal {A}$ function Speckey. Bottom right: One iteration of the key schedule of Sparx-64/128.

Sparx-64/128. The structure of Sparx-64 is reminiscent of a Feistel network of eight steps. Each step consists of $r_a = 3$ rounds of the ARX-box $\mathcal {A}$, (i.e. three rounds of Speckey) on each branch. The Feistel function $\mathcal {L}$ is a linear involutive permutation $\mathcal {L}: \mathbb {F} _2^{32} \rightarrow \mathbb {F} _2^{32}$ inspired by [8]. Given the left 32-bit state word $x \,\Vert \, y$, the input is split into 16-bit parts x, y, and is mapped to

$$\begin{aligned} \mathcal {L} (x \,\Vert \, y)&{\mathop {=}\limits ^{\text {def}}} (x \oplus ((x \oplus y) \lll 8)) \,\Vert \, (y \oplus ((x \oplus y) \lll 8)). \end{aligned}$$

We denote the 64-bit state after Round r interchangeably as $(L_r, R_r)$ $=$ $(X^0_r$ $\,\Vert \,$ $X^1_r, X^2_r$ $\,\Vert \,$ $X^3_r)$ $=$ $(X^L_r$ $\,\Vert \,$ $Y^L_r, X^R_r$ $\,\Vert \,$ $Y^R_r)$, and the round key used in Round r interchangeably as $(K^L_r$, $K^R_r$) $=$ ($K^0_r \,\Vert \, K^1_r$, $K^2_r \,\Vert \, K^3_r)$.

The Key Schedule of Sparx-64. The 128-bit secret key of Sparx-64/128 is divided into four initial 32-bit words $(\kappa _0^0, \kappa _0^1, \kappa _0^2, \kappa _0^3)$. In each step, the key schedule transforms the leftmost 32-bit word $\kappa _{s}^0$ in one iteration of the ARX-box $\mathcal {A}$, adds the output to the right neighboring word $\kappa _{s}^1$, adds a round constant $RC_i$ to the rightmost 16-bit half of $\kappa _{2s}^3$ to prevent slide attacks, and finally rotates the four words by one position to the right. The $r_a = 3$ leftmost words $\kappa _{2s}^0$, $\kappa _{2s}^1$, $\kappa _{2s}^2$ are used as round keys for the first, second, and third round of the left branch of Step $s+1$; the $r_a = 3$ left-most words $\kappa _{2s+1}^0$, $\kappa _{2s+1}^1$, $\kappa _{2s+1}^2$ are used for the first, second, and third round of the right branch of Step $s+1$. For example, $(\kappa _0^0, \kappa _0^1, \kappa _0^2)$ are used as round keys for the left branch in the first step, and $(\kappa _1^0, \kappa _1^1, \kappa _1^2)$ are used as round keys for the right branch in the first step.

Table 2. Parameters of the individual versions of Sparx.

2.2 Properties

As observed by Abdelkhalek et al. [1], one can obtain the rounds keys for 2.5 consecutive rounds by guessing only 64 bit of key material. More precisely, one obtains the round keys for Round $3r+1$ and the round key for the right 32-bit branch in Round $3r+2$ by guessing the 64 bit of the key material of Round 3r:

Property 1

Given $\kappa ^2_{s+1}$ and $\kappa ^3_{s+1}$, one can directly derive the key words $\kappa ^2_s = \kappa ^3_{s+1}$, $\kappa ^0_{s+2} = \kappa ^3_{s+1}$, $\kappa ^1_{2s+3} = \mathcal {A} (\kappa ^0_{s+2})$, and $\kappa ^0_{s+3} = \kappa ^2_{s+1}$.

We learnt Property 2 from Leurent [10].

Property 2

Assume, $\Delta \in \mathbb {F} _2^{n}$ is a fixed difference, and $x^0, \ldots , x^m \in \mathbb {F} _2^{n}$ represent m values for which the goal is to find pairs $(x^i, x^j)$ that result in $x^i\,\oplus \,x^j = \Delta$. Then, one can define a linear function $F: \mathbb {F} _2^{n} \rightarrow \mathbb {F} _2^{n}$ with rank $n-1$, s.t. $F(\Delta ) = 0^{n}$; thus, all pairs $(x^i, x^j)$ with $x^i \oplus x^j = \Delta$ will collide in $F(x^i) = F(x^j)$.

It finds pairs with some difference without studying all combinations of pairs but by comparing their outputs from F. One can reduce the rank of F to $n-d$ so that outputs of F collide if and only if their inputs have one of $2^d$ differences.

3 Boomerang and Rectangle Attacks

Boomerang attacks, as proposed by Wagner [15], allow an attacker to concatenate two short differentials with high probability when long differentials with sufficient probability are absent or hard to find. In the basic setting, an adversary splits an encryption function $E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n$ into two subciphers $E = E_2 \circ E_1$, s.t. $E(P) {\mathop {=}\limits ^{\text {def}}} E_2(E_1(P))$. Then, it considers a first differential $\alpha \rightarrow \beta$ with probability p over $E_1$ and a second differential $\gamma \rightarrow \delta$ with probability q over $E_2$. These are often called upper and lower differentials or trails, respectively. They can then be combined in a chosen-plaintext and adaptive chosen-ciphertext attack to construct a boomerang distinguisher consisting of the following steps:

• 1. Choose a plaintext pair $(P, P')$ with difference $\alpha = P\,\oplus \,P'$ and encrypt it through E to obtain its ciphertext pair $(C, C')$ with difference $\beta$.

• 2. Derive $D = C\,\oplus \,\delta$ and $D' = C'\,\oplus \,\delta$ (the $\delta$-shift) and decrypt D and $D'$ through $E^{-1}$ to obtain the corresponding plaintext pair $(Q, Q')$.

• 3. If the plaintext pair $(Q, Q')$ has difference $\alpha = Q \oplus Q'$, then $(P, P', Q, Q')$ form a correct quartet.

Proposition 1

For a quartet $(P, P', Q, Q')$, there exists a differential with an input difference $\alpha$ for $P' = P \oplus \alpha$, $Q' = Q \oplus \alpha$, and a corresponding output difference $\beta$ for $U' = U \oplus \beta$, $V' = V \oplus \beta$ with probability p. If we consider a differential $\delta \rightarrow \gamma$ with input difference $D = C \oplus \delta$, $D' = C' \oplus \delta$ and a corresponding output difference $\gamma$ for $V = U \oplus \gamma$, it holds with probability q that $V' = U' \oplus \gamma$. Then, we can connect both differentials if we consider $V = U \oplus \gamma$, it follows that $V' = V \oplus \beta = (U \oplus \gamma ) \oplus \beta = (U \oplus \beta ) \oplus \gamma = U' \oplus \gamma$.

Calculating the probabilities for a correct quartet requires to consider both plaintext pairs $(P, P')$ and $(Q, Q')$ and results in a probability of $(pq)^2$. For the differentials to exist, the resulting probability has to satisfy $(pq)^2 \ge 2^{-n/2}$.

The probability of a correct quartet can be increased if one fixes input differences $\alpha$ and $\delta$ but allows all possible differences for $\beta$ and $\gamma$, requiring only that $\beta \ne \gamma$. A boomerang distinguisher would then consider all trails of the form $\alpha \rightarrow \beta '$ for the upper trail and $\delta \rightarrow \gamma '$ for the lower trail. This increases the probability to $(\widehat{p} \widehat{q})^2$ where $\widehat{p} = \sqrt{\sum _{\beta '} {\Pr }^2\left[ \alpha \rightarrow \beta ' \right] }$ and $\widehat{q} = \sqrt{\sum _{\gamma '} {\Pr }^2\left[ \delta \rightarrow \gamma ' \right] }$ where $\widehat{p}$ is evaluated over $E_1$ and $\widehat{q}$ over $E_2^{-1}$, respectively.

The Rectangle Attack. In boomerang attacks, the adversary needs to query its oracles with chosen plaintexts and adaptively chosen ciphertexts. Since our boomerang attack will have to guess a considerable amount of key bits, which would require an oracle query for every obtained text and key guess, we will employ a rectangle attack instead. Rectangle attacks [3] have been derived from the amplified boomerang [9], both of which transform the boomerang into a purely chosen-plaintext attack (or chosen-ciphertext if the adversary starts from the opposite direction). The core idea is to encrypt many pairs $(P, P')$ with difference $P' \oplus P = \alpha$ in the hope that some of those will form a quartet with the desired differences in the middle with probability $2^{-n}$. Given N plaintext pairs, the number of correct quartets is reduced to $N^2 \cdot 2^{-n} \cdot (\widehat{p} \widehat{q})^2$. Note that two pairs $(U, U')$ and $(V, V')$ can be combined in two distinct ways to a quartet in the middle: $U \oplus V = U' \oplus V' = \beta$ or $U \oplus U' = V \oplus V' = \beta$. [4] presented further improvements to the technique. The disadvantages of rectangle compared to boomerang attacks are the increased data complexity and the large number of potential quartets that have to be filtered to find correct quartets.

Ladder Switch. There exist a few approaches for increasing the transitional probability of boomerang trails in the middle. Two well-known approaches are the Feistel switch and the ladder switch; recently, Sasaki et al. [6] observed a number of more ways. Here, we concentrate on the ladder switch by [5]. It exploits that start and end of upper and lower trails can be located at different locations for each part of the state. For Sparx, it is intuitive to consider full steps: e.g., assume that the top trail has a nonzero difference in the left branch through the step in the middle. If the right branch has a zero difference in the left branch, one can put the switch for the left branch before the step and consider it to be part of the bottom trail, which has probability one. Clearly, this approach can be generalized further to probabilities smaller than one. For Sparx, an optimal switch has one active (e.g., the left) and one inactive (e.g., the right) branch in the top trail, and mirrored in the bottom trail (e.g., right active and left inactive), which allows to pass the step in the middle with probability one.

4 Differential Trails and Boomerang Distinguishers

We employed a two-step approach: first, we searched for optimal differential characteristics for up to ten rounds of Sparx-64. Those formed the base of the wrapping rounds before and after the boomerang switches. Thereupon, we considered three interesting types of boomerangs over five steps.

Table 3. An optimal six-round differential trail.

Table 4. Optimal differentials through up to ten rounds of Sparx-64; t is the run time of each search.

Table 5. Top (left to right): best trails found for our differentials of Type 1a, Type 1b, Type 1c, and Type 1d. Middle: best trails found for our differentials of Type 2a, Type 2b, Type 2d, and Type 2e. Bottom: Type 2c, Type 3a, Type 3b, and Type 3c. $\varSigma$ denotes the sum of $h_w$ over all rounds.

4.1 Searching Optimal Differential Trails

We implemented variants of Sparx in CryptoSMT [12], an open- source tool based on the SAT/SMT solvers CryptoMiniSat [11] and STP [14] to search for optimal differential characteristics¹. In this case, the problem to find optimal differential characteristics is modeled as a Boolean satisfiability problem, and can then be solved by a SAT solver. As the differential model of a cipher can be rather complex, we modeled the problem as a more general SMT (Satisfiability Modular Theories) problem. The difference to SAT problems is that SMT problems can express richer languages where, e.g., sets of variables can be expressed as predicates or the problem can be modeled on word level. We describe the differential behavior of Sparx using the CVC language. This allows us to define specific constraints that can be used to limit the search space for the SAT solver. The solver then tries to find all possible valid differential characteristics for the given parameters with increasing probability.

Table 3 shows an optimal six-round differential trail. Note that $h_w$ denotes $h_w = -\log _2(p)$, for the differential probability p through a round. One can observe that optimal differential characteristics for Sparx-64 possess an hourglass structure, i.e., the number of active bits is minimal in the middle and increases outwards. Using the probability of the best characteristic is often assumed to be an adequate approximation of the probability of the best differential. However, this approximation is not always sufficiently accurate for ARX-based ciphers. Therefore, we tried to evaluate the probability of differentials where feasible. For the best differentials for Sparx-64, we provide an overview in Table 4.

Types of Differential Characteristics. After searching differentials incrementality for a given interval of rounds, we searched for optimal characteristics among the following types. The first category consists of single-step characteristics:

• Type 1a. Arbitrary single-step characteristics.

• Type 1b. Single-step characteristics with two active branches that have a single active branch after the step.

• Type 1c. Single-step characteristics with two active branches that have a single active branch before the step.

• Type 1d. Single-step characteristics with two active branches that have a single active branch before and afterwards.

The best characteristic for single-steps is a Type 1a characteristic with the left branch all zeros. Type 1d is especially interesting for our truncated-differential attack. The second category consists of two-step characteristics, that are also used in our boomerang/rectangle distinguishers:

• Type 2a. Two-step top characteristics which collide after the XOR in the right branch after the first step.

• Type 2b. Two-step bottom characteristics with only the left branch active at the first step.

• Type 2c. Two-step characteristics where only the left branch is active in the first, and therefore only the right branch is active in the second step.

• Type 2d. 4.5-round versions of Type 2a, but only two rounds before the collision for the left and one round before for the right branch.

• Type 2e. We further investigated the versions of Type 2a where the first step covers only one round.

We use the two-step characteristic of Type 2c for the top trail and Type 2b for the bottom trail of our rectangle distinguisher. We further considered three-step characteristics for boomerang/rectangle attacks in our third category:

• Type 3a. Three-step characteristics where both branches are active in the first step, and only one branch is active in the subsequent steps, as is used in both top and bottom trail of the single- sided bottom type of boomerang.

• Type 3b. Three-step characteristics where the first two steps are of Type 3a, and both branches are active in the third step.

• Type 3c. 7.5-round versions of Type 3b, where only one round is considered for the first step.

Our results for the best characteristics found are summarized in Table 5.

Fig. 2.

Types of five-step boomerangs. White $\mathcal {A} ^3$ boxes are inactive (zero difference); gray $\mathcal {A} ^3$-boxes are active (non-zero difference). Hatched $\mathcal {A} ^3$ boxes indicate active branches that do not have to be taken into account at the switch.

4.2 Boomerangs

From the combination of the best identified characteristics, we continued to form boomerangs. We considered three types of boomerangs over five steps.

• Free middle. This type exploits that we can obtain the middle step for free if we choose our top and bottom trails such that one of them possesses a zero difference in the left branch, and the other one has a zero difference in the right branch, which is a direct application of the Ladder switch. We can obtain a five-step boomerang in this way, but have active differences in both branches in the first and in the fifth step of the wrapping rounds.

• Single-sided bottom. This type has both branches active at the start of the top trail, but only one active branch at the end of the bottom trail.

• Single-sided top. This type has both branches active at the end of the bottom trail, but only one active branch at the beginning of the top trail.

As examples, the former two types are visualized in Fig. 2.

From our experiments, it became clear soon that free-middle boomerangs possessed higher probabilities. Table 6 summarizes the best boomerang that consist of a single characteristic that we could find for one up to five steps. Through a single step, there exist various boomerangs with probability one:

$$\begin{aligned} \Pr \left[ (\Delta L_0, \Delta R_0) \xrightarrow {\text {1 step}} (\Delta L_3, \Delta R_3) \right] = 1, \end{aligned}$$

for all characteristics with $\Delta L_0 = 0$ and $\Delta L_3 = \mathcal {L} (\Delta R_3)$; alternatively, it also holds for all characteristics with $\Delta R_0 = \Delta R_3 = 0$.

Over two steps, there exist two-step boomerangs with

$$\begin{aligned} \Pr \left[ (\Delta L_0, \Delta R_0) \xrightarrow {\text {2 steps}} (\Delta L_6, \Delta R_6) \right] \ge 2^{-6}, \end{aligned}$$

namely for characteristics of the form

• $\Delta L_0 = 0$ and $\Delta R_0 \in \{\texttt {28000010}, \texttt {00400000} \}$ and $\Delta L_6 = \mathcal {L} (\Delta R_6)$, or

• $\Delta R_0 = 0$ and $\Delta R_6 \in \{\texttt {81008102}, \texttt {8000840a} \}$ and $\Delta L_6 = \mathcal {L} (\Delta R_6)$.

For three steps, the best boomerangs have probability $2^{-12}$, using the single-step characteristic with the highest probability of Type 1a for the top trail, and a similar characteristic mirrored vertically and starting from the bottom difference $(\Delta L_9, \Delta R_9) = (\texttt {83008302}, \texttt {81008102})$. Similarly, we obtain from the combination of the characteristics of Type 2a (as the top trail) and Type 1a (horizontally mirrored, as the bottom trail; this is a free-middle boomerang) boomerangs with probability of $2^{-44}$ over four steps. Over five steps, the highest theoretical probability of a boomerang with fixed characteristics results from combining a characteristic of Type 2a with the highest probability at the top with a characteristic of Type 2b with the highest probability at the bottom.

Near-optimal Differential Trails. Boomerangs that employ a single characteristic are of limited expressiveness in practice as we noticed strong differential clustering effects in Sparx. For boomerangs, they are particularly strong in the switching rounds. Our purpose was to find good boomerangs of five steps, where we focused on the free-middle approach. We used the best characteristics of Type 1b and Type 2a as top and Type 1a and Type 2b as bottom trails as a base to study their probability empirically over a feasible subset of the three steps in the middle. Moreover, our automated search for optimal differential characteristics yielded many near-optimal differentials with probability slightly smaller than that of the optimal ones; as one could anticipate, this small change in the probability stemmed from the fact that bits adjacent to the active bits in the optimal differentials were also active in the near-optimal ones, mainly in the first or the last round. Hence, we also considered those near-optimal trails in our investigation of potential start and end differences for boomerangs. The subset of our results is given in Table 7. We used a variant of them for our rectangle attack in Sect. 6.

Table 6. Best found boomerangs on step-reduced Sparx-64/128; for up to three steps, we verified them experimentally with 100 random keys and $2^{20}$ random pairs each. Values in parentheses are products of the empirical probabilities over the three steps in the middle from Table 7 with the theoretical probabilities over the remaining step(s).

Table 7. Relevant experimental probabilities of free-middle boomerangs over three steps. Values represent $-\log _2(p)$, where p is the average probability of correct quartets from 100 test runs of random independent keys with $2^{30}$ random text pairs each.

5 Truncated-Differential Attack on Sparx-64/128

Table 8. The truncated differential trail through 16 rounds. A * symbol marks a truncated difference which can take any possible value.

High-Level View. This section describes a truncated-differential attack on 16-round Sparx-64/128. On a high level, the Feistel-like structure allows generic trails that pass through almost two steps so that only one branch is active. The core observation of our attack is the existence of differentials of Type 1d, i.e., trails that have an inactive branch before and after a step with probability ${\gg }{2^{-32}}$. One such trail is illustrated in Table 8. The trail is truncated after Round 9; thereupon, its precise differences are irrelevant as long as it will cancel in the right branch after the linear layer, and the zero-difference branch can propagate through two further steps (i.e. Rounds $13{-}18$ in Table 8). Thus, an adversary can observe that only a single branch will be active after five steps; the final linear layer can then be easily inverted. On the downside, the probability of truncated trails must exceed $2^{-32}$ for a useful distinguisher.

To ensure a sufficient probability of the differential, we employ Property 1 at the plaintext side to reduce the number of steps to trace through. So, we obtain the round keys of Round 3, 4, and that for the right branch of Round 5 from guessing only 64 bits of key material. At the ciphertext side, we choose structures of $2^{32}$ texts, such that all texts in a structure have a constant value in the right branch, and iterate over all values on the left branch through Rounds $16{-}18$. In the following, we mount a chosen-ciphertext attack on 16-round Sparx-64/128 covering Rounds 3 through 18; the used differential trail is given in Table 8.

Structures and Sets. We choose $2^m$ structures of $2^{32}$ ciphertexts each from a base text $S_{18}^0 = (L_{18}, R_{18})$, and $2^{32}-1$ derived texts $S_{18}^{i} = (L_{18}^i, R_{18})$ from iterating over all $2^{32}$ values $L_{18}$, and derive the $2^{32}$ ciphertexts $C^i \leftarrow \mathcal {L} (S^i)$ that form the structure. Since we employ all $2^{32}$ possible values for the right branch of Rounds 16 to 18, their $2^{63}$ pairs will form all possible differences in this branch about $2^{31}$ times at any point until the end of Round 12, i.e., $\Delta _{12}$. From experiments, we observed that the truncated differential $(\texttt {80008000}, \texttt {80008000})$ leads to $(\texttt {00000000}, \texttt {********})$ with probability $2^{-17.36}$. Hence, there is a subset of good differences $\Delta _{12}$ that can lead to $(\texttt {80008000}, \texttt {80008000})$ with this accumulated probability. Since we have $2^{31}$ pairs for each such $\Delta _{12}$, we expect that there are about $2^{31-17.36} \approx 2^{13.64}$ pairs with $\Delta _9 = (\texttt {80008000}, \texttt {80008000})$, and $2^{13.64-6-5} = 2^{2.64}$ pairs that follow our trail up to $\Delta _5$. We have approximately $2^{63}$ pairs in a structure that have our desired difference with probability $2^{-64}$, so we expect $2^{-1}$ false positive pairs from the structure.

Experimental Verification. We verified a variant of our distinguisher experimentally using 100 random keys and $2^{32}$ random pairs. For practicality, we considered it in encryption direction, i.e., we chose random pairs with start difference $(\Delta L_5$, $\Delta R_5) = (\texttt {00000000}$, $\texttt {0a204205})$, encrypted them to the states after Round 18 and inverted the final linear layer. On average, we obtained $2^{3.75}$ pairs with zero difference in the right branch, which corresponds to a probability of $2^{3.75-32} = 2^{-28.25}$, which is close to the expected $2^{-28.36}$.

Attack Steps. Using Property 2, we define a linear function $F: \mathbb {F} _2^{32} \,\times \,\mathbb {F} _2^{32} \rightarrow \mathbb {F} _2^{64}$ with rank $n-1 = 63$, so that $F(\Delta ) = 0^{64}$ for $\Delta = (\texttt {00000000}$, $\texttt {0a204205})$. The attack consists of the following steps:

• 1. Construct $2^m$ structures as described above. For each structure, request the corresponding $2^{32}$ plaintexts $P^i$ from a 16-round decryption oracle.

• 2. Initialize a list $\mathcal {K}$ of $2^{64}$ key counters.

• 3. For each of the $2^{64}$ guesses of $K^0_2, K^1_2, K^2_2, K^3_2$, i.e., the key of Round 2:

  • 3.1 Re-encrypt all plaintexts over one round until the state after the linear layer of Round 3 and store them in a list $\mathcal {H}$ according to the values of their left branches. Only consider pairs that collide in $L_3$ after the application of the linear layer $\mathcal {L}$, and store those in a distinct list $\mathcal {H} '$.

  • 3.2 For all texts, compute $(L_3, R_5)$, apply $F(R_r)$, and store the updated states in $\mathcal {H}$. Discard all pairs that do not collide. For each colliding pair, increment the counter for the current key candidate in $\mathcal {K}$.

• 4. Output the keys in descending order of their corresponding counters.

Complexity. The computational complexity results from:

• Step 1 requires $2^{m+32}$ 16-round decryptions. We assume that the computational costs for decryption and encryption are equal.

• Step 3.1 requires $2^{64} \cdot 2^{m+32} \cdot 1/16 \cdot 2 \approx 2^{m+92}$ encryption equivalents since we consider one out of 16 rounds. From the $\left( {\begin{array}{c}2^{32}\\ 2\end{array}}\right) \approx 2^{63}$ pairs of one structure, we expect $2^{63-32} = 2^{31}$ false positive pairs for each structure at this step.

• We approximate the costs for a call to F by those of a call to two Speckey rounds since both branches are used. The complexity of Step 3.2 is therefore given by $2^{64} \cdot 2^{31+m} \cdot 4/32 \approx 2^{m+92}$ encryption equivalents on average. We expect about $2^{63-64} = 2^{-1}$ false-positive pairs per structure and key candidate, whereas we have $2^{31-28.36} \approx 2^{2.64}$ correct pairs for the correct key candidate, again per structure.

The computational complexity sums to

$$\begin{aligned} 2^{m+32} + 2^{m+92} + 2^{m+92} \approx 2^{m+93} \text { Encryptions.} \end{aligned}$$

The memory complexity stems from storing a byte counter for the current key candidate, i.e., $2^{64} \cdot 8/64 = 2^{61}$ states, plus $2^{32}$ texts. The data complexity is given by $2^{m+32}$. A single structure, i.e., $m = 1$, suffices to obtain at least two correct pairs for the correct round-key candidate.

6 Rectangle Attack on 16-Round Sparx-64/128

High-Level View. This section describes a rectangle attack on 16-round Sparx-64/128. Our attack starts after the second round of the cipher, i.e., it starts with Round 3. Again, we guess 64 key bits to get through Rounds 3 and 4 and the right branch of Round 5. The attack covers then Rounds 3 through 18.

Differential Trails. Table 9 illustrates the employed differential trails. The top trail covers Rounds 3 through 9 and the right part of Rounds 10 to 12 since the right part contains a zero difference which propagates for free through the $\mathcal {A} ^3$ box of Rounds 10 to 12. The bottom trail covers Rounds 13 through 18, and the left part of Rounds 10 through 12 in decryption direction. Again, the bottom trail has a zero difference in that part, which propagates for free through the $\mathcal {A} ^3$ box backwards through Rounds 12 through Round 10.

Table 9. Our used differential characteristic through the top (left) and bottom (right) trail for our 16-round rectangle attack on Sparx-64/128.

Again, we experimentally verified the boomerang switch in the middle. From 100 experiments with random keys and $2^{26}$ independently at random chosen pairs $(P, P')$ with difference $\alpha = (\texttt {80008000}$, $\texttt {80008000})$, encrypted through three steps to $(C, C')$, applied the $\delta$-shift $(\texttt {80008000}$, $\texttt {80008000})$ to obtain $(D, D')$, decrypted those back to $(Q, Q')$, and counted the number of times that $Q \oplus Q' = \alpha$. We observed an average probability of approximately $2^{-20.18}$. So, for the correct key, we obtain a probability of approximately $(\widehat{p} \widehat{q})^2 \approx \left( 2^{-2}\right) ^2 \cdot 2^{-20.18} \cdot \left( 2^{-14}\right) ^2 \approx 2^{-52.18}$ for a valid quartet.

Attack Procedure. Choose a linear function $F: \mathbb {F} _2^{64} \rightarrow \mathbb {F} _2^{64}$ of rank 63 s.t. $F(\Delta L_4 \,\Vert \, \Delta R_5) = 0^{64}$. The attack consists of the following steps:

• 1. Initialize a list of key counters $\mathcal {L}$ to zero, for all $2^{64}$ possible values for the round keys of Round 2.

• 2. Initialize two empty hash maps $\mathcal {P}$ and $\mathcal {Q}$. Choose $2^{m}$ ciphertext pairs (C, D) with difference $(\texttt {2a102a10}$, $\texttt {850a9520})$, and ask for their corresponding plaintexts (P, Q). Store the pairs into $\mathcal {P}$ indexed by P.

• 3. For each of the $2^{64}$ guesses of $(K^0_2, K^1_2, K^2_2, K^3_2)$:

  • 3.1 Partially re-encrypt all plaintext pairs (P, Q) to their corresponding states $(L^P_4, R^P_5)$ and $(L^Q_4, R^Q_5)$.

  • 3.2 Apply $F((L_4, R_5))$ to all states and store the corresponding outputs $(\widehat{L}^P_4, \widehat{R}^P_5)$ and $(\widehat{L}^Q_4, \widehat{R}^Q_5)$ into a hash table $\mathcal {Q}$. Only consider pairs of pairs $p = (\widehat{L}^P_4, \widehat{R}^P_5)$, $q = (\widehat{L}^Q_4, \widehat{R}^Q_5)$, $p' = (\widehat{L}^{P'}_4, \widehat{R}^{P'}_5)$, $q' = (\widehat{L}^{Q'}_4, \widehat{R}^{Q'}_5)$ that collide in either $(p, q) = (p', q')$ or $(p, q) = (q', p')$ and discard all further quartets. We expect $2^{2m} \cdot 2^{2 \cdot -64} \approx 2^{2m-128}$ quartets on average.

  • 3.3 If a quartet survives, increment the counter for the current key guess. Choose a plaintext pair with our desired difference – w.l.o.g., $(p, p')$ – from the current quartet, and check for all remaining key bits if it follows our path until Round 6. If yes, encrypt it further roundwise until Round 9. If all roundwise checks pass, check for p if it encrypts to ciphertext C. If yes, test again for $(q, q')$ and output the key candidate if it also matches.

• 4. If no key candidate has been returned, return $\bot$.

For $m = 58.6$ pairs, we can expect $(2^m\widehat{p} \widehat{q})^2/2^n \approx 2^{117.2} \cdot 2^{-52.18}/2^{64} \approx 2$ valid quartets for the correct key guess. In contrast, we can expect $2^{117.2 - 2 \cdot 64} = 2^{-10.8}$ quartets for a wrong key guess.

Complexity. The computational complexity results from:

• Step 2 requires $2 \cdot 2^{58.6} \approx 2^{59.6}$ 16-round decryptions. We assume that the computational costs for a decryption and encryption are equal.

• Steps 3.1 and 3.2 require $2^{64} \cdot 2 \cdot 2^{m} \cdot 6/32 \approx 2^{122.2}$ encryption equivalents since we consider five out of 32 Speckey rounds in the 16-round cipher for re-encryption and approximate the costs for computing F by the costs of a Speckey round.

• Step 3.2 will require $2^{64} \cdot 2 \cdot 2^{m} = 2^{m+65}$ memory accesses (MAs) and comparisons.

• Step 3.3 will require at most $2^{64} \cdot 2^{2m-128} \cdot 2^{64} \approx 2^{117.2}$ encryption equivalents to identify the correct key.

Hence, the computations are upper bounded by approximately

$$\begin{aligned} 2^{59.6} + 2^{122.2} \approx 2^{122.2} \text { encryptions}\quad \text {and}\quad 2^{59.6} + 2^{123.6}&\approx 2^{123.6} \text { MAs.} \end{aligned}$$

The data complexity is upper bounded by $2^{59.6}$ chosen ciphertexts. The memory complexity is upper bounded by storing at most $4 \cdot 2^{59.6}$ states at a time, which is equivalent to storing approximately $2^{61.6}$ states.

7 Conclusion

This work presents two standard differential attacks using truncated differentials and rectangle attacks on 16-round Sparx-64/128. The former attack builds upon a nine-round (three-step) differential trail that is extended by a six-round (two-step) truncated trail. Adopting the observation by Abdelkhalek et al. [1], we can turn the distinguishers into a 16-round chosen-ciphertext attack and recover the round keys by just guessing 64-bit of the key material. Our truncated- differential attack requires approximately $2^{32}$ chosen ciphertexts, about $2^{32}$ states, and approximately $2^{93}$ encryption equivalents. Our proposed rectangle attack exploits the Feistel structure of Sparx using differential trails with inactive branches over their middle step; similarly, the yoyo attack in the full version of this paper [2] profits from the structure over the end. It may be interesting for further studies to investigate yoyo cycles of more iterations of en- and decryption.

We stress that our attacks do not threaten the security of Sparx-64/128, but provide deeper insights in its security against attacks in the single-key setting. We can observe a strong clustering effect of many differential characteristics in our studies and exploit them in our attacks; it remains subject to further studies to employ them for further rounds. For public verification and future works, our trails, tests, and implementations of Sparx-64/128 will be published into the public domain².