Keywords

1 Ιntroduction

During the hydraulic design and management the first step is the assessment of the hydrological variables. Unfortunately, these cannot be treated with crisp values. There is plenty of academic works and engineering experience about the probabilistic implementation of the hydrological variables. However, the couple between the statistic and theoretical probability distributions is not without problems.

Thus, in this article, for first time, a hybrid model is proposed to improve the matching between the sample and the normal probability distribution function. This hybrid approach treats the couple between the normal distribution density function and the observed probabilities enhanced by the using of fuzzy linear regression.

An advantage of the probabilistic approach as a choice to treat the uncertainty is the exploitation of the cumulative empirical (observed) probability distribution in order to test the goodness-of-fit for a theoretical probability distribution with respect to the historical sample. In this article, a hybrid methodology is developed so that, both the concepts of the observed probability and the flexibility of the fuzzy approach can be used.

More specifically, the main idea is to express the probabilistic parameters as fuzzy numbers and thus, the flexibility of the fuzzy arithmetic and other concepts of the fuzzy sets can be exploited.

Mainly, in contrast with the traditional approaches, the proposed hybrid, fuzzy enhanced methodology produces a fuzzy relation which can be seen as a fuzzy band, which contains all the observed data, that is, all the pairs between the observed hydrological values and the observed probability. This fuzzy relation (it can be seen as a fuzzy band) is modulated based on the fuzzy linear regression model of Tanaka (1987). Therefore, the thresholds of fuzziness are modulated with respect to the observed data, by following a constraining optimization problem, and not by following an a- priori information as in several cases of the fuzzy optimization problems.

Fuzzy linear regression may be a useful tool to express functional relationships between variables, especially when the available data are not sufficient (Ganoulis 2009). For instance, Kitsikoudis et al. (2016) employed a fuzzy regression to produce a lower and an upper limit for the critical dimensionless shear stress. Thus, we avoid the ambiguity of selecting a threshold for the initiation of motion, and hence, the model provides a smoother transition to the state of general movement.

More generally, for studying complex physical phenomena such as the interconnection between adjacent watersheds (Tsakiris et al. 2006), the rainfall-runoff process without all the involved parameters, the use of fuzzy models should be investigated. In contrast to the statistical regression, fuzzy regression analysis has no error term, while the uncertainty is incorporated in the model by means of fuzzy numbers (Spiliotis and Bellos 2016; Papadopoulos and Sirpi 2004).

In brief, the proposed methodology can be divided into three steps: modulation of the data (an analysis based on the conventional statistical approach), application of the fuzzy linear regression (which concludes to a constrained optimization problem) and finally evaluation of the solution achieved where the assumption of the considered pdf is tested. The proposed methodology concludes to a fuzzy relation between the probability and the hydrological variables simultaneously with the fuzzy assessment of the mean value and the standard deviation. In this work, the methodology is developed for normal distributed annual cumulative precipitation.

2 Basic Notions

Let a historical sample. The rank order method involves ordering the data from the largest hydrological value to the smallest hydrological value, assigning a rank of 1 to the largest value and a rank of N to the smallest value. Based on the Weibull empirical distribution (which is widely used in the Greek regions) to compute the plotting position probabilities, the cumulative exceedance probability can be calculated as follows (e.g. Chow et al. 1988):

$$ Prob\left( {P \ge p} \right) = \frac{m}{{{N} + 1}} $$
(1)

where m is the rank of the value in a list ordered by descending magnitude (Chow et al. 1988). As P many hydrological random variables can be considered. In this work we focus on the annual cumulative precipitation.

It is evident that the cumulative probability of non-exceedance can be calculated as follows based on the exceedance probability (given that that P is a continuous random variable and according to the common practice in hydrology):

$$ Prob\left( {P \le p} \right) = 1 - \frac{m}{{{N} + 1}} $$
(2)

The return period of an event, T, of a given magnitude may be viewed as the

average recurrence length of time (usually years) between events equaling or exceeding a specified magnitude (Chow et al. 1998):

$$ Prob\left( {P \le p} \right) = 1 - \frac{1}{T} $$
(3)

In case of the normal distribution, based on the calculated unbiased estimation of the mean and the standard deviation with respect to the available historical sample, \( \bar{p},s, \) correspondingly, it holds:

$$ Prob\left( {P \le p_{T} } \right) = \left( {1 - \frac{1}{T}} \right)\text{,} $$
(4)
$$ \left. {\begin{array}{*{20}l} {Prob\left( {P \le p_{T} } \right) = \left( {1 - \frac{1}{T}} \right) = \varPhi \left( {{Z}_{T} } \right)} \hfill \\ {Z_{T} = \frac{{p_{T} - \bar{p}}}{\sigma }} \hfill \\ \end{array} } \right\} \Rightarrow \frac{{p_{T} - \bar{p}}}{\sigma } = Z_{T} \Rightarrow p_{T} = \bar{p} + \sigma Z_{T} $$
(5)

where Z is the standardized normal variable and \( p_{T} \) is the magnitude of the event having a return period T.

A used technique in hydrology is to investigate a linear relation between the standardized normal variable Z and the hydrological variable (here the cumulative annual precipitation), instead of the probability plot. Similarly with the probability plot, the calculation of the normal variable Z is based on the empirical probability of the sample which corresponds to each pair between the standardized normal variable and the examined hydrological variable:

$$ p_{T} = a_{0}^{{}} + a_{1} Z_{T} $$
(6)

It is desirable, that the coefficients α 0 and α 1 to be close to the unbiased estimation of the mean value and the standard deviation of the sample, \( \bar{p} \) and s respectively, as it occurs in the case of the crisp formulation. In the past, the graphical method with specified paper plots were used in order to rather manually identify the proper curve and the corresponding parameters. Also the conventional regression can be used to determine the parameters α 0 and α 1 .

The main proposal of this article is the application of the fuzzy linear regression to determine the parameters α 0 and α 1 . That is,

$$ \tilde{p}_{T} = \tilde{a}_{0}^{{}} + \tilde{a}_{1} Z_{T} $$
(7)

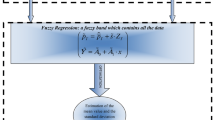
An interesting point is that additionally, a fuzzy approach for the mean value and the standard deviation can be achieved. The proposed methodology is graphically presented in Fig. 1 and it will be presented bellow more analytically. As aforementioned, the produced fuzzy band will contain all the observed data and this is one significant advantage of the proposed methodology.

Fig. 1.
figure 1

Schematic representation of the proposed methodology.

Full size image

3 Proposed Methodology

The aim of the proposed methodology is to provide a fuzzy relation between the standardized normal variable Z and the examined hydrological variable simultaneously with a fuzzy estimation of the mean value and the standard deviation. The proposed methodology is based on the observed probabilities of the sample and thereafter the fuzzy regression is used. However, the proposed method holds is the hypothesis of normal distributed random variable holds. Next the main three steps of the proposed methodology are presented.

3.1 Modulating the Independent and Dependent Variables

Firstly, the data are ordered from the largest hydrological value to the smallest hydrological value, assigning a rank. Then, based on the Weibull 1939 empirical distribution, the cumulative non-exceedance probability is calculated. Subsequently, a hypothesis must be made about the theoretical probability distribution. Here, the normal distribution is examined. Hence, the standardized normal variable Z can be determined for each pair of data based on the empirical probabilities.

As aforementioned the independent variable is the Z T term. To determine the Z T term the following two assumptions must be made:

$$ Z_{T} =\Phi ^{ - 1} \left( {1 - \frac{m}{N + 1}} \right) $$
(8)

It should be clarified that the standard statistical tests of fitness can be used only to predispose the probability distribution. The proposed methodology does not use the standard statistical tests of fitness. Furthermore, the evaluation of the solution achieved is based on the fuzzy solution and not on any conventional statistical test.

3.2 Applying Fuzzy Regression

Fuzzy linear regression model proposed by Tanaka (1987) has the following form:

$$ \begin{aligned} & \tilde{Y}_{j} = \tilde{A}_{0} + \tilde{A}_{1} x_{1j} + \ldots \tilde{A}_{i} x_{ij} + \ldots . + \tilde{A}_{\rm N} x_{{{\rm N}j}} \\ & {\text{with}}\;j{ = 1,} \ldots ,\,M,\,i = 1, \ldots ,N \\ \end{aligned} $$
(9)

where N is the number of independent variables, M is the number of data, and \( \tilde{A}_{i} \) = (ai, ci)L are symmetric fuzzy triangular numbers selected as coefficients (Fig. 2) (Papadopoulos and Sirpi 2004):

Fig. 2.
figure 2

Fuzzy triangular symmetrical number.

Full size image

In case of normally distributed annual cumulative precipitation, the following fuzzy linear regression model is examined:

$$ \begin{array}{*{20}l} {\tilde{p}_{Tj} = \tilde{\bar{p}} + \tilde{s} \cdot Z_{T,j} } \hfill \\ {(\tilde{Y}_{j} = \tilde{A}_{0} + \tilde{A}_{1} \cdot x_{1j} )} \hfill \\ \end{array} $$
(10)

where \( \tilde{P}_{Tj} \) is the fuzzy assessment of the hydrological magnitude of the event (dependent variable) having a return period T for the jth set of data.

With respect to Eq. 10, the mean and the standard deviation \( \tilde{\bar{p}},\tilde{s} \) respectively, are the fuzzy coefficients (fuzzy symmetrical triangular numbers in this application). The fuzzy coefficients are determined based on the Tanaka fuzzy linear regression method. The standardized normal variable is the independent variable, which takes only crisp values as well as the dependent variable which is the annual cumulative precipitation.

Thus, the proposed methodology can produce a fuzzy estimation of the mean value and the standard deviation. This fuzzy estimation is based on the fuzzy regression and hence, it is founded with the respect to the data. However, we highlight that the fuzzy estimation of the mean value and the standard deviation is related with the assumption of the normal distribution.

In this point it should be referred, that many problems of fuzzy logic, as the fuzzy arithmetic, the fuzzy linear regression e.t.c. are formulated with the aim of a-cuts. The α-cuts could be characterized as the bridge between the fuzzy and the crisp (conventional) sets. The α–cut set of the fuzzy number A (with 0 < α ≤ 1) is defined as follows:

$$ \left[ {\text{A}} \right]_{\upalpha} = \left\{ {\left. {\text{x}} \right|\upmu_{\text{A}} ({\text{x}}) \ge\upalpha} \right\} $$
(11)

Note that the α–cut set is a crisp set determined from the fuzzy set according to a selected value of the membership function and, alternatively, a fuzzy set can be practically decomposed to a significant number of α–cut sets. In case of α= 0, the above definition (Eq. 14) can be modified without the equality in order to describe the zero-cut (Kitsikoudis et al. 2016; Spiliotis and Bellos 2016; Buckley and Eslami 2002).

The concept of inclusion can be defined with respect to the a-cut. The inclusion of a fuzzy set A to the fuzzy set B with the associated degree \( 0 \le h \le 1 \) (it is a critical point, that the inclusion property is based on a selected h-cut between all the other α-cuts) is defined as follows:

$$ \left[ {\text{A}} \right]_{\text{h}} \subseteq \left[ {\text{B}} \right]_{\text{h}} $$
(12)

The constraints of the problems are modulated based on the concept of inclusion. Thus, all the data (which are crisp numbers) must be included in the produced fuzzy band:

$$ p_{\text{j}} \in \left[ {p_{{\text{h,j}}}^{\text{L}} \text{,}\,\,\,\,p_{{\text{h,j}}}^{\text{R}} } \right] $$
(13)

By taking into account the fuzzy arithmetic, for a selected level h, the inclusion constraints in case the decision variables are selected to be symmetrical triangular numbers, are equivalent to:

$$ \left\{ {\begin{array}{*{20}l} {{Inclusion}\,\,{Constraints}}\,\, \hfill \\ {\left( {\,\bar{p} + s \cdot \,{Z}_{{{T},{j}}} } \right) - \left( {1 - h} \right)\left( {\,w_{{\bar{p}}} + w_{s} \left| {Z_{{{T},j}} } \right|} \right) = p_{{\text{h,j}}}^{\text{L}} \le \text{p}_{\text{j}} } \hfill \\ {\left( {\,\bar{p} + s \cdot \,Z_{{{T},j}} } \right) + \left( {1 - h} \right)\left( {\,w_{{\bar{p}}} + w_{s} \left| {Z_{{{T},j}} } \right|} \right) = \text{p}_{{\text{h,j}}}^{\text{R}} \ge \text{p}_{\text{j}} } \hfill \\ {w_{{_{{\bar{p}}} }} ,\,\,w_{s} \ge 0} \hfill \\ \end{array} } \right. $$
(14)

Since the fuzzy regression leads to a constrained optimization problem, the assessment of the fitness is based on the produced fuzzy band. The smaller the fuzzy band, the more proper the fuzzy model becomes. Hence, Tanaka (1987) suggested the minimization of the sum of the produced fuzzy semi-spreads for all the data (Spiliotis and Bellos 2016; Kitsikoudis et al. 2016; Papadopoulos and Sirpi 2004):

$$ Min \, J\,\left( { = \sum\limits_{j = 1}^{M} {w_{pj} } = \left\{ {M \cdot w_{{\bar{p}}} + w_{s} \sum\limits_{j = 1}^{M} {\left| {Z_{{{T},j}} } \right|} } \right\}} \right) \,(objective \, function) $$
(15)

The above measure is the sum of all the produced semi-spreads (from the fuzzy band) for all the observed data.

Therefore, in brief, based on the Tanaka methodology, the parameters of the fuzzy coefficients, that is, the centers and the widths of the fuzzy coefficients, are determined by solving a constrained optimization problem (Eqs. 14 and 15). In the examined problem, these fuzzy coefficients can be viewed as an estimation of the mean value and the standard deviation. The objective function is selected to be the total semi-spread of the fuzzy outputs.

3.3 Evaluation of the Solution Achieved

In fact, every fuzzy regression problem based on Tanaka formulation will have a solution, and hence, the magnitude of the produced fuzzy band could be a criterion about how successful is the proposed fuzzy linear transformation. A large semi-spread, J, indicates that the axis of the standardized normal variable Z must be changed and hence, other probability distribution could be examined (Spiliotis and Papadopoulos 2017).

Another measure to test the suitability of the examined probability distribution is proposed, F which is the Euclidean distance between the central values of the mean value and the standard deviation with the unbiased (usual statistical) estimation of the same variables, \( \hat{\mu },\,\,\hat{\sigma } \):

$$ F = \sqrt {\left( {\bar{p} - \hat{\mu }} \right)^{2} + \left( {s - \hat{\sigma }} \right)^{2} } $$
(16)

4 Application in Case of Annual Rainfall Time Series

The meteorological station of Aldeia Nova de São Bento belongs to the National Information System for the Water Resources (SNIRH) of Portugal. The station is located inside the area of Guadiana between the Guadiana River and the Portugal – Spain border, as shown in Fig. 3 (Angelidis et al. 2012). The data cover a large time span, from 1931 up to 2007. The proposed methodology was applied to express the annual cumulative rainfall with respect to the for normal distributed rainfall.

Fig. 3.
figure 3

Location of the Aldeia Nova de São Bento rain station.

Full size image

Indeed, by using the statistical test of Kolmogorov-Smirnov (K-S) with an interval confidence (1−α) = 0.80, the result indicates that the normal distribution can be used to express the annual rainfall in Aldeia Nova de São Bento. As aforementioned the statistical test is not used directly in the proposed methodology, but it simply indicates a proper algebraic transformation.

Fuzzy regression is applied for a selected h = 0 whilst fuzzy symmetrical triangular numbers were selected as fuzzy coefficients. Finally, based on the above assumptions, the problem of fuzzy regression leads to a linear programming problem. All in all, the following fuzzy curve between the standard normal random variable Z and the annual rainfall is produced through the constrained optimization problem according to Eqs. 14 and 15 (Fig. 4):

Fig. 4.
figure 4

Observed data, fuzzy and conventional (crisp) regression between the standardize normal variable Z (based on the observed cumulative non-exceedance probabilities) and the annual rainfall of the sample.

Full size image
$$ \tilde{P}_{T} = \left( { 1 6 1. 9 6,\,\, 3. 5 8} \right)_{L} \cdot {Z}_{T} + \left( {551.50,\,39.95} \right)_{L} $$
(17)

where \( \tilde{P}_{T} \) is a fuzzy number which represents the estimated cumulative annual runoff (dependent variable). Hence, by adopting the normal distribution, according to Eq. 17, we achieve simultaneously a fuzzy assessment of the mean value \( \left( {551.50,\,39.95} \right)_{L} \) and the standard deviation \( \left( { 1 6 1. 9 6,\,\, 3. 5 8} \right)_{L} \). The first term in the bracket expresses the central value (Fig. 2) and the second term, the semi-width of each fuzzy symmetrical triangular number. In general, a fuzzy symmetrical number is Q special case of the fuzzy number.

The objective function of the fuzzy regression problem which expresses the total uncertainty is equal to:

$$ J_{N} = 75 \cdot 3 9. 9 5+ 3. 5 8\sum\limits_{j = 1}^{75} {\left| {Z_{{{T},j}} } \right|} { = 3,202} . 8 $$
(18)

In addition, from the fuzzy curve (Eq. 17), it is easy to see that the central values of the fuzzy coefficients, which can be seen as a fuzzy approximation of the mean value and the standard deviation, are very close to their unbiased estimation based on the historical sample \( \left( {\hat{\mu } = 545.50,\,\hat{\sigma } = 159.91} \right) \). Indeed, the Euclidean distance between the central values of the mean value and the standard deviation with the unbiased (usual statistical) estimation of the same variables, \( \hat{\mu },\,\hat{\sigma } \) has a rather small value:

$$ F = \sqrt {\left( {545.50 - 551.50} \right)^{2} + \left( { 1 6 1. 9 6- 159.91} \right)^{2} } = 6.34\,{\text{mm}} $$
(19)

The values of both the objective function (Eq. 18) and the proposed measure F (Eq. 19) indicate that the fuzzified normal distribution can be used to express the annual cumulative rainfall in Aldeia Nova de São Bento. Therefore, from the application, it is evident that the objective function and the proposed measure of suitability, F, provide us the opportunity to test the suitability of the initial hypothesis about the use of the normal distribution as the theoretical probability distribution.

Another interesting perspective to discuss is the proposed methodology in relation with the statistic test of Kolmogorov–Smirnov. The statistic test of Kolmogorov–Smirnov involves the absolute values of the distance between the observed probability and the probability value from the adopted theoretical cumulative distribution function for all the sample. By applying the proposed methodology, all the data, that is, each pair which includes the value of the hydrological value and the corresponding non-exceedance empirical probability is included in the produced fuzzy band at least to some degree (Fig. 4).

An interesting point is that the proposed fuzzy estimation of the mean value and the standard deviation is more founded to fuzzy logic and without subjective choices which must be made by the user, compared with Sfiris et al. 2014 approach. According to Sfiris et al. 2014, the mean value and the standard deviation are estimated as fuzzy numbers starting from the conventional probabilistic confidence interval. However, a confidence interval must be selected from the user, in order to move from the probabilistic approach to the fuzzy approach. In addition, the transition from the asymptotic to non asymptotic membership function was done by selecting a suitable function. According to the new methodology, the mean value and the standard deviation are estimated as fuzzy numbers based on the observed data by following a fuzzy regression approach without specific considerations from the user. Furthermore, two measures to test the validity of the method are proposed.

It should be clarified also that the proposed methodology is based on the probabilistic model with crisp data whilst the fuzziness arises from the matching between the theoretical probability distribution function and the observed probabilities. The method should not be confused with either methods which are based on fuzzy data (fuzzy sample, e.g. Viertl 2011) or methods with starting from a probabilistic approach conclude to a fuzzy approach (e.g. Sfiris and Papadopoulos 2014).

Another interesting point for further investigation is the use of several theoretical distributions. Then, the use of the suitability measure F and the value of the objective function J can be seen as the criteria according to which the selection of the suitable theoretical probability distribution can be done. Spiliotis and Papadopoulos 2017 have already studied a similar methodology in case of lognormal theoretical probability distribution. In general, the proposed methodology could be expanded based on the frequency factor method which includes also the proposed analysis based on the standardized variable Z for normal probability distribution.

As aforementioned in case that a significant fuzzy band is produced, then the first think will be the change of the theoretical pdf and this can be seen as the main challenge for further investigation. However, the use of new techniques of fuzzy regression should also be investigated. For instance, it could be investigated the use of more sophisticated objective functions which will contain both the centers and the widths of the fuzzy coefficients. Hence, a new objective function could try either to increase the possibility of equality between the observations and fuzzy intervals (Shakouri et al. 2017) or could incorporate simultaneously with the fuzzy spreads the sum of possibility grade in the objective function (Yabuuchi 2017). Alternatively, ideas from goal programming could be applied in order to reduce the impact of outliers (Kitsikoudis et al. 2016) and hence, the objective function is changed accordingly.

5 Concluding Remarks

A hybrid combination between the problem of coupling between the observed probabilities and the normal distribution with the aim of fuzzy linear regression analysis is proposed in this article. According to the proposed methodology, the exploitation of the empirical probability function can be achieved together with a fuzzy approach. The key of the proposed methodology is the application of the fuzzy linear regression model of Tanaka in order to achieve a linear relation with fuzzy numbers as coefficients. In addition, based on the proposed fuzzy regression, the mean value and the standard deviation are determined as fuzzy coefficients.

Hence, the proposed innovative methodology provides the opportunity to achieve simultaneously a fuzzy assessment of the mean value and the standard deviation based on the solution of the fuzzy linear regression. In contrast, the application of the conventional crisp regression products crisp numbers as coefficients, which differ from the unbiased estimation of the mean value and the standard deviation. The proposed fuzzy estimation of the mean value and the standard deviation is desirable to include the unbiased estimation of the mean value and the standard deviation.

Indeed, the measure of the distance between the central values of the mean value and the standard deviation with the unbiased (usual statistical) estimations together with its fuzziness, are proposed also as measures of suitability in order to test the validation of the method and consequently the selected probability pdf.

Another interesting property of the proposed methodology is that the proposed fuzzy band includes all the data at least at some degree. In general, the proposed methodology improves the matching between the sample of the hydrological variable and the used probability distribution.