Fine-Grained Semantics for Probabilistic Programs

Abstract

Probabilistic programming is an emerging technique for modeling processes involving uncertainty. Thus, it is important to ensure these programs are assigned precise formal semantics that also cleanly handle typical exceptions such as non-termination or division by zero. However, existing semantics of probabilistic programs do not fully accommodate different exceptions and their interaction, often ignoring some or conflating multiple ones into a single exception state, making it impossible to distinguish exceptions or to study their interaction.

In this paper, we provide an expressive probabilistic programming language together with a fine-grained measure-theoretic denotational semantics that handles and distinguishes non-termination, observation failures and error states. We then investigate the properties of this semantics, focusing on the interaction of different kinds of exceptions. Our work helps to better understand the intricacies of probabilistic programs and ensures their behavior matches the intended semantics.

1 Introduction

A probabilistic programming language allows probabilistic models to be specified independently of the particular inference algorithms that make predictions using the model. Probabilistic programs are formed using standard language primitives as well as constructs for drawing random values and conditioning. The overall approach is general and applicable to many different settings (e.g., building cognitive models). In recent years, the interest in probabilistic programming systems has grown rapidly with various languages and probabilistic inference algorithms (ranging from approximate to exact). Examples include [10, 11, 13, 14, 25,26,27, 29, 36]; for a recent survey, please see [15]. An important branch of recent probabilistic programming research is concerned with providing a suitable semantics for these programs enabling one to formally reason about the program’s behaviors [2,3,4, 33,34,35].

Often, probabilistic programs require access to primitives that may result in unwanted behavior. For example, the standard deviation $\sigma$ of a Gaussian distribution must be positive (sampling from a Gaussian distribution with negative standard deviation should result in an error). If a program samples from a Gaussian distribution with a non-constant standard deviation, it is in general undecidable if that standard deviation is guaranteed to be positive. A similar situation occurs for while loops: except in some trivial cases, it is hard to decide if a program terminates with probability one (even harder than checking termination of deterministic programs [20]). However, general while loops are important for many probabilistic programs. As an example, a Markov Chain Monte Carlo sampler is essentially a special probabilistic program, which in practice requires a non-trivial stopping criterion (see e.g. [6] for such a stopping criterion). In addition to offering primitives that may result in such unwanted behavior, many probabilistic programming languages also provide an ${{\mathbf {\mathtt{{observe}}}}}\,$ primitive that intuitively allows to filter out executions violating some constraint.

Motivation. Measure-theoretic denotational semantics for probabilistic programs is desirable as it enables reasoning about probabilistic programs within the rigorous and general framework of measure theory. While existing research has made substantial progress towards a rigorous semantic foundation of probabilistic programming, existing denotational semantics based on measure theory usually conflate failing ${{\mathbf {\mathtt{{observe}}}}}\,$ statements (i.e., conditioning), error states and non-termination, often modeling at least some of these as missing weight in a sub-probability measure (we show why this is practically problematic in later examples). This means that even semantically, it is impossible to distinguish these types of exceptions¹. However, distinguishing exceptions is essential for a solid understanding of probabilistic programs: it is insufficient if the semantics of a probabilistic programming language can only express that something went wrong during the execution of the program, lacking the capability to distinguish for example non-termination and errors. Concretely, programmers often want to avoid non-termination and assertion failure, while observation failure is acceptable (or even desirable). When a program runs into an exception, the programmer should be able determine the type of exception, from the semantics.

This Work. This paper presents a clean denotational semantics for a Turing complete first-order probabilistic programming language that supports mixing continuous and discrete distributions, arrays, observations, partial functions and loops. This semantics distinguishes observation failures, error states and non-termination by tracking them as explicit program states. Our semantics allows for fine-grained reasoning, such as determining the termination probability of a probabilistic program making observations from a sequence of concrete values.

In addition, we explain the consequences of our treatment of exceptions by providing interesting examples and properties of our semantics, such as commutativity in the absence of exceptions, or associativity regardless of the presence of exceptions. We also investigate the interaction between exceptions and the ${{\mathbf {\mathtt{{score}}}}}\,$ primitive, concluding in particular that the probability of non-termination cannot be defined in this case. ${{\mathbf {\mathtt{{score}}}}}\,$ intuitively allows to increase or decrease the probability of specific runs of a program (for more details, see Sect. 5.3).

2 Overview

In this section we demonstrate several important features of our probabilistic programming language (PPL) using examples, followed by a discussion involving different kinds of exception interactions.

2.1 Features of Probabilistic Programs

In the following, we informally discuss the most important features of our PPL.

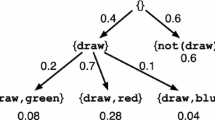
Discrete and Continuous Primitive Distributions. Listing 1 illustrates a simple Gaussian mixture model (the figure only shows the function body). Depending on the outcome of a fair coin flip x (resulting in 0 or 1), y is sampled from a Gaussian distribution with mean 0 or mean 2 (and standard deviation 1). Note that in our PPL, we represent ${{\mathbf {\mathtt{{gauss}}}}}\, (\cdot ,\cdot )$ by the more general construct ${{\mathbf {\mathtt{{sampleFrom}}}}}\, _f(\cdot ,\cdot )$, with $f:\mathbb {R}\times [0,\infty ) \rightarrow \mathbb {R}\rightarrow \mathbb {R}$ being the probability density function of the Gaussian distribution $f(\mu ,\sigma )(x)=\frac{1}{\sqrt{2\pi \sigma ^2}}e^{-\frac{(x-\mu )^2}{2\sigma ^2}}$.

Conditioning. Listing 2 samples two independent values from the uniform distribution on the interval [0, 1] and conditions the possible values of x and y on the observation $x+y>1$ before returning x. Intuitively, the first two lines express a-priori knowledge about the uncertain values of x and y. Then, a measurement determines that $x+y$ is greater than 1. We combine this new information with the existing knowledge. Because $x+y>1$ is more likely for larger values of x, the return value has larger weight on larger values. Formally, our semantics handles ${{\mathbf {\mathtt{{observe}}}}}\,$ by introducing an extra program state for observation failure . Hence, the probability distribution after the third line of Listing 2 will put weight $\frac{1}{2}$ on and weight $\frac{1}{2}$ on those x and y satisfying $x+y>1$.

In practice, one will usually condition the output distribution on there being no observation failure (). For discrete distributions, this amounts to computing:

where x is the outcome of the program (a value, non-termination or an error) and $Pr[X=x]$ is the probability that the program results in x. Of course, this conditioning only works when the probability of is not 1. Note that tracking the probability of has the practical benefit of rendering the (often expensive) marginalization unnecessary.

Other semantics often use sub-probability measures to express failed observations [4, 34, 35]. These semantics would say that Listing 2 results in a return value between 0 and 1 with probability $\frac{1}{2}$ (and infer that the missing weight of $\frac{1}{2}$ is due to failed observations). We believe one should improve upon this approach as the semantics only implicitly states that the program sometimes fails an observation. Further, this strategy only allows tracking a single kind of exception (in this case, failed observations). This has led some works to conflate observation failure and non-termination [18, 34]. We believe there is an important distinction between the two: observation failure means that the program behavior is inconsistent with observed facts, non-termination means that the program did not return a result.

Listing 3 illustrates that it is not possible to condition parts of the program on there being no observation failure. In Listing 3, conditioning the first branch $x:=0;{{\mathbf {\mathtt{{observe}}}}}\, ({{\mathbf {\mathtt{{flip}}}}}\, \,{(\frac{1}{2})})$ on there being no observation failure yields $Pr[x=0]=1$, rendering the observation irrelevant. The same situation arises for the second branch. Hence, conditioning the two branches in isolation yields $Pr[x=0]=\frac{1}{2}$ instead of $Pr[x=0]=\frac{2}{3}$.

Loops. Listing 4 shows a probabilistic program with a while loop. It samples from the ${{\mathbf {\mathtt{{geometric}}}}}\, (\frac{1}{2})$ distribution, which counts the number of failures (${{\mathbf {\mathtt{{flip}}}}}\,$ returns 0) until the first success occurs (${{\mathbf {\mathtt{{flip}}}}}\,$ returns 1). This program terminates with probability 1, but it is of course possible that a probabilistic program fails to terminate with positive probability. Listing 5 demonstrates this possibility.

Listing 5 modifies x until either $x=0$ or $x=10$. In each iteration, x is either increased or decreased, each with probability $\frac{1}{2}$. If x reaches 0, the loop terminates. If x reaches 10, the loop never terminates. By symmetry, both termination and non-termination are equally likely. Hence, the program either returns 0 or does not terminate, each with probability $\frac{1}{2}$.

Other semantics often use sub-probability measures to express non-termination [4, 23]. Thus, these semantics would say that Listing 5 results in 0 with probability $\frac{1}{2}$ (and nothing else). We propose to track the probability of non-termination explicitly by an additional state $\circlearrowleft$, just as we track the probability of observation failure ().

Partial Functions. Many functions that are practically useful are only partial (meaning they are not defined for some inputs). Examples include ${{\mathbf {\mathtt{{uniform}}}}}\, (a,b)$ (undefined for $b<a$) and $\sqrt{x}$ (undefined for $x<0$). Listing 6 shows an example program using $\sqrt{x}$. Usually, semantics do not explicitly address partial functions [23, 24, 28, 33] or use partial functions without dealing with failure (e.g. [19] use ${{\mathbf {\mathtt{{Bernoulli}}}}}\, (p)$ without stating what happens if $p \notin [0,1]$). Most of these languages could use a sub-probability distribution that misses weight in the presence of errors (in these languages, this results in conflating errors with non-termination and observation failures).

We introduce a third exception state $\bot$ that can be produced when partial functions are evaluated outside of their domain. Thus, Listing 6 results in $\bot$ with probability $\frac{1}{2}$ and returns a value from [0, 1] with probability $\frac{1}{2}$ (larger values are more likely). Some previous work uses an error state to capture failing computations, but does not propagate this failure implicitly [34, 35]. In particular, if an early expression in a long program may fail evaluating $\sqrt{-4}$, every expression in the program that depends on this failing computation has to check whether an exception has occurred. While it may seem possible to skip the rest of the function in case of a failing computation (by applying the pattern ${{\mathbf {\mathtt{{if }}}}}\, (x=\bot ) \; \{{{\mathbf {\mathtt{{return }}}}}\, \, \bot \} {{\mathbf {\mathtt{{ else }}}}}\, \{\text {rest of function}\}\,$), this is non-modular and does not address the result of the function being used in other parts of a program.

Although our semantics treat $\bot$ and similarly, there is an important distinction between the two: $\bot$ means the program terminated due to an error, while means that according to observed evidence, the program did not actually run.

Fig. 1.

Visual comparison of the exception handling capabilities of different semantics. For example, $\circlearrowleft$ is filled in [34] because its semantics can handle non-termination. However, the intersection between $\circlearrowleft$ and is not filled because [34] cannot distinguish non-termination from observation failure.

2.2 Interaction of Exception States

Next, we illustrate the interaction of different exception states. We explain how our semantics handles these interactions when compared to existing semantics. Fig. 1 gives an overview of which existing semantics can handle which (interactions of) exceptions. We note that our semantics could easily distinguish more kinds of exceptions, such as division by zero or out of bounds accesses to arrays.

Non-termination and Observation Failure. Listing 7 shows a program that has been investigated in [22]. Based on the observations, it only admits a single behavior, namely always sampling $x=0$ in the third line. This behavior results in non-termination, but it occurs with probability 0. Hence, the program fails an observation (ending up in state ) with probability 1. If we try to condition on not failing any observation (by rescaling appropriately), this results in a division by 0, because the probability of not failing any observation is 0.

The semantics of Listing 7 thus only has weight on , and does not allow conditioning on not failing any observation. This is also the solution that [22] proposes, but in our case, we can formally back up this claim with our semantics.

Other languages handle both non-termination and observation failure by sub-probability distributions, which makes it impossible to conclude that the missing weight is due to observation failure (and not due to non-termination) [4, 24, 34]. The semantics in [28] cannot directly express that the missing weight is due to observation failure (rather, the semantics are undefined due to a division by zero). However, the semantics enables a careful reader to determine that the missing weight is due to observation failure (by investigating the conditional weakest precondition and the conditional weakest liberal precondition). Some other languages can express neither while loops nor observations [23, 33, 35].

Assertions and Non-termination. For some programs, it is useful to check assumptions explicitly. For example, the implementation of the factorial function in Listing 8 explicitly checks whether x is a valid argument to the factorial function. If $x \notin \mathbb {N}$, the program should run into an error (i.e. only have weight on $\bot$). If $x \in \mathbb {N}$, the program should return x! (i.e. only have weight on x!). This example illustrates that earlier exceptions (like failing an assertion) should bypass later exceptions (like non-termination, which occurs for $x \notin \mathbb {N}$ if the programmer forgets the first two assertions). This is not surprising, given that this is also the semantics of exceptions in most deterministic languages. Most existing semantics either cannot express Listing 8 ([23, 34] have no assertions, [35] has no iteration) or cannot distinguish failing an assertion from non-termination [24, 28, 33]. The consequence of the latter is that removing the first two assertions from Listing 8 does not affect the semantics. Handling assertion failure by sum types (as e.g. in [34]) could be a solution, but would force the programmer to deal with assertion failure explicitly. Only the semantics in [4] has the expressiveness to implicitly handle assertion errors in Listing 8 without conflating those errors with non-termination.

Listing 9 shows a different interaction between non-termination and failing assertions. Here, even though the loop condition is always true, the first iteration of the loop will run into an exception. Thus, Listing 9 results in $\bot$ with probability 1. Again, this behavior should not be surprising given the behavior of deterministic languages. For Listing 9, conflating errors with non-termination means the program semantics cannot express that the missing weight is due to an error and not due to non-termination.

Observation Failure and Assertion Failure. In our PPL, earlier exceptions bypass later exceptions, as illustrated in Listing 8. However, because we are operating in a probabilistic language, exceptions can occur probabilistically. Listing 10 shows a program that may run into an observation failure, or into an assertion failure, or neither. If it runs into an observation failure (with probability $\frac{1}{2}$), it bypasses the rest of the program, resulting in with probability $\frac{1}{2}$ and in $\bot$ with probability $\frac{1}{4}$. Conditioning on the absence of observation failures, the probability of $\bot$ is $\frac{1}{2}$.

An important observation is that reordering the two statements of Listing 10 will result in a different behavior. This is the case, even though there is no obvious data-flow between the two statements. This is in sharp contrast to the semantics in [34], which guarantee (in the absence of exceptions) that only data flow is relevant and that expressions can be reordered. Our semantics illustrate that even if there is no explicit data-dependency, some seemingly obvious properties (like commutativity) may not hold in the presence of exceptions. Some languages either cannot express Listing 10 ([23, 33] lack observations), cannot distinguish observation failure from assertion failure [24] or cannot handle exceptions implicitly [34, 35].

Summary. In this section, we showed examples of probabilistic programs that exhibit non-termination, observation failures and errors. Then, we provided examples that show how these exceptions can interact, and explained how existing semantics handle these interactions.

3 Preliminaries

In this section, we provide the necessary theory. Most of the material is standard, however, our treatment of exception states is interesting and important for providing semantics to probabilistic programs in the presence of exceptions. All key lemmas (together with additional definitions and examples) are proven in Appendix A.

Natural Numbers, [n], Iverson Brackets, Restriction of Functions. We include 0 in the natural numbers, so that $\mathbb {N}:= \{ 0, 1, \dots \}$. For $n \in \mathbb {N}$, $[n] := \{ 1, \dots , n \}$. The Iverson brackets $[\cdot ]$ are defined by $[b]=1$ if b is true and $[b]=0$ if b is false. A particular application of the Iverson brackets is to characterize the indicator function of a specific set S by $[x \in S]$. For a function $f :X \rightarrow Y$ and a subset of the domain $S \subseteq X$, f restricted to S is denoted by $f_{\mid S} :S \rightarrow Y$.

Set of Variables, Generating Tuples, Preservation of Properties, Singleton Set. Let $Vars$ be a set of admissible variable names. We refer to the elements of $Vars$ by x, y, z and $x_i,y_i,z_i,v_i,w_i$, for $i \in \mathbb {N}$. For $v \in A$ and $n \in \mathbb {N}$, $v!n := (v,\dots ,v) \in A^n$ denotes the tuple containing n copies of v. A function $f :A^n \rightarrow A$ preserves a property if whenever $a_1, \dots , a_n \in A$ have that property, $f(a_1, \dots , a_n) \in A$ has that property. Let $\mathbb {1}$ denote the set which only contains the empty tuple (), i.e. $\mathbb {1}:= \{ () \}$. For sets of tuples $S \subseteq \prod _{i=1}^n A_i$, there is an isomorphism $S \times \mathbb {1}\simeq \mathbb {1}\times S \simeq S$. This isomorphism is intuitive and we sometimes silently apply it.

Exception States, Lifting Functions to Exception States. We allow the extension of sets with some symbols that stand for the occurrence of special events in a program. This is important because it allows us to capture the event that a given program runs into specific exceptions. Let be a (countable) set of exception states. We denote by $\overline{A} := A \cup \mathcal {X}$ the set A extended with $\mathcal {X}$ (we require that $A \cap \mathcal {X}= \emptyset$). Intuitively, $\bot$ corresponds to assertion failures, corresponds to observation failures and $\circlearrowleft$ corresponds to non-termination. For a function $f :A \rightarrow B$, f lifted to exception states, denoted by $\overline{f} :\overline{A} \rightarrow \overline{B}$ is defined by $\overline{f}(a)=a$ if $a \in \mathcal {X}$ and $\overline{f}(a)=f(a)$ if $a \notin \mathcal {X}$. For a function $f :\prod _{i=1}^n A_i \rightarrow B$, f lifted to exception states, denoted by $\overline{f} :\prod _{i=1}^n \overline{A_i} \rightarrow \overline{B}$, propagates the first exception in its arguments, or evaluates f if none of its arguments are exceptions. Formally, it is defined by $\overline{f}(a_1, \dots , a_n)=a_1$ if $a_1 \in \mathcal {X}$, $\overline{f}(a_1, \dots , a_n)=a_2$ if $a_1 \notin \mathcal {X}$ and $a_2 \in \mathcal {X}$, and so on. Only if $a_1, \dots , a_n \notin \mathcal {X}$, we have $\overline{f}(a_1, \dots , a_n) =f(a_1, \dots , a_n)$. Thus, $\overline{f}(\circlearrowleft ,a,\bot )=\circlearrowleft$. In particular, we write $\overline{(a,b)}$ for lifting the tupling function, resulting in for example . To remove notation clutter, we do not distinguish the two different liftings $\overline{f} :\overline{A} \rightarrow \overline{B}$ and $\overline{f} :\prod _{i=1}^n \overline{A_i} \rightarrow \overline{B}$ notationally. Whenever we write $\overline{f}$, it will be clear from the context which lifting we mean. We write $S \overline{\times } T$ for $\{ \overline{(s,t)} \mid s \in S, t \in T\}$.

Records. A record is a special type of tuple indexed by variable names. For sets $(S_i)_{i \in [n]}$, a record $r \in \prod _{i=1}^n (x_i :S_i)$ has the form $r = \{ x_1 \mapsto v_1, \dots , x_n \mapsto v_n \}$, where $v_i \in S_i$, with the convenient shorthand $r = \{ x_i \mapsto v_i \}_{i \in [n]}$. We can access the elements of a record by their name: $r[x_i] = v_i$.

In what follows, we provide the measure theoretic background necessary to express our semantics.

$\sigma$-algebra, Measurable Set, $\sigma$-algebra Generated by a Set, Measurable Space, Measurable Functions. Let A be some set. A set $\varSigma _A \subseteq \mathcal {P}\left( A\right)$ is called a $\sigma$-algebra on A if it satisfies three conditions: $A \in \varSigma _A$, $\varSigma _A$ is closed under complements ($S \in \varSigma _A$ implies $A \backslash S \in \varSigma _A$) and $\varSigma _A$ is closed under countable unions (for any collection $\{ S_i \}_{i \in \mathbb {N}}$ with $S_i \in \varSigma _A$, we have $\bigcup _{i \in \mathbb {N}} S_i \in \varSigma _A$). The elements of $\varSigma _A$ are called measurable sets. For any set A, a trivial $\sigma$-algebra on A is its power set $\mathcal {P}\left( A\right)$. Unfortunately, the power set often contains sets that do not behave well. To come up with a $\sigma$-algebra on A whose sets do behave well, we often start with a set $S \subseteq \mathcal {P}\left( A\right)$ that is not a $\sigma$-algebra and extend it until we get a $\sigma$-algebra. For this purpose, let A be some set and $S \subseteq \mathcal {P}\left( A\right)$ a collection of subsets of A. The $\sigma$-algebra generated by S denoted by $\sigma (S)$ is the smallest $\sigma$-algebra that contains S. Formally, $\sigma (S)$ is the intersection of all $\sigma$-algebras on A containing S. For a set A and a $\sigma$-algebra $\varSigma _A$ on A, $(A, \varSigma _A)$ is called a measurable space. We often leave $\varSigma _A$ implicit; whenever it is not mentioned explicitly, it is clear from the context. Table 1 provides the implicit $\sigma$-algebras for some common sets. As an example, some elements of $\varSigma _{\overline{\mathbb {R}}}$ include $[0,1] \cup \{ \bot \}$ and $\{ 1,3,\pi \}$. For measurable spaces $(A, \varSigma _A)$ and $(B, \varSigma _B)$, a function $f :A \rightarrow B$ is called measurable, if $\forall S \in \varSigma _B :f^{-1}(S) \in \varSigma _A$. Here, $f^{-1}(S) := \{ a \in A :f(a) \in S \}$. If one is familiar with the notion of Lebesgue measurable functions, note that our definition does not include all Lebesgue measurable functions. As a motivation to why we need measurable functions, consider the following scenario. We know the distribution of some variable x, and want to know the distribution of $y=f(x)$. To figure out how likely it is that $y \in S$ for a measurable set S, we can determine how likely it is that $x \in f^{-1}(S)$, because $f^{-1}(S)$ is guaranteed to be a measurable set.

Table 1. Implicit $\sigma$-algebras on common sets, for measurable spaces $(A,\varSigma _A)$, $(A_i, \varSigma _{A_i})$

Measures, Examples of Measures. For a measurable space $(A,\varSigma _A)$, a function $\mu :\varSigma _A \rightarrow [0,\infty ]$ is called a measure on A if it satisfies two properties: null empty set ($\mu (\emptyset ) = 0$) and countable additivity (for any countable collection $\{ S_i \}_{i \in \mathcal {I}}$ of pairwise disjoint sets $S_i \in \varSigma _A$, we have $\mu \left( \bigcup _{i \in \mathcal {I}} S_i \right) = \sum _{i \in \mathcal {I}} \mu (S_i)$). Measures allow us to quantify the probability that a certain result lies in a measurable set. For example, $\mu ([1,2])$ can be interpreted as the probability that the outcome of a process is between 1 and 2.

The Lebesgue measure $\lambda :\mathcal {B} \rightarrow [0,\infty ]$ is the (unique) measure that satisfies $\lambda ([a,b])=b-a$ for all $a,b \in \mathbb {R}$ with $a \le b$. The zero measure $\mathbf {0}:\varSigma _A \rightarrow [0,\infty ]$ is defined by $\mathbf {0}(S) = 0$ for all $S \in \varSigma _A$. For a measurable space $(A, \varSigma _A)$ and some $a \in A$, the $\textit{Dirac measure}$ $\delta _a :\varSigma _A \rightarrow [0,\infty ]$ is defined by $\delta _a(S) = [a \in S]$.

Unfortunately, there are measures that do not satisfy some important properties (for example, they may not satisfy Fubini’s theorem, which we discuss later on). The usual way to deal with this is to restrict our attention to $\sigma$-finite measures, which are well-known and were studied in great detail. However, $\sigma$-finite measures are too restrictive for our purposes. In particular, the s-finite kernels that we introduce later on can induce measures that are not $\sigma$-finite. This is why in the following, we work with s-finite measures. Table 2 gives an overview of the different kinds of measures that are important for understanding our work. The expression $1/2\cdot \delta _1$ stands for the pointwise multiplication of the measure $\delta _1$ by $1\text {/}2$: $1\text {/}2\cdot \delta _1 = \lambda S.\,1/2\cdot \delta _1(S)$. Here, the $\lambda$ refers to $\lambda$-abstraction and not to the Lebesgue measure. To distinguish the two $\lambda$s, we always write “$\lambda x.$” (with a dot) when we refer to $\lambda$-abstraction. For more details on the definitions and for proofs about the provided examples, see Appendix A.1.

Table 2. Definition and comparison of different measures $\mu :\varSigma _A \rightarrow [0,\infty ]$ on measurable spaces $(A,\varSigma _A)$. Reading the table top-down, we get from the most restrictive definition to the most permissive definition. For example, any sub-probability measure is also a $\sigma$-finite measure. We also provide an example for each type of measure that is not an example of the more restrictive type of measure. For example, the Lebesgue measure $\lambda$ is $\sigma$-finite but not s-finite.

Product of Measures, Product of Measures in the Presence of Exception States. For s-finite measures $\mu :\varSigma _A \rightarrow [0, \infty ]$ and $\mu ' :\varSigma _B \rightarrow [0, \infty ]$, we denote the product of measures by $\mu \times \mu ' :\varSigma _{A \times B} \rightarrow [0, \infty ]$, and define it by

$$ (\mu \times \mu ')(S) = \int _{a \in A} \int _{b \in B} [(a,b) \in S] \mu '(db) \mu (da) $$

For s-finite measures $\mu :\varSigma _{\overline{A}} \rightarrow [0, \infty ]$ and $\mu ' :\varSigma _{\overline{B}} \rightarrow [0, \infty ]$, we denote the lifted product of measures by $\mu \overline{\times } \mu ' :\varSigma _{\overline{A \times B}} \rightarrow [0, \infty ]$ and define it using the lifted tupling function: $(\mu \overline{\times } \mu ')(S) = \int _{a \in \overline{A}} \int _{b \in \overline{B}} [\overline{(a,b)} \in S] \mu '(db) \mu (da)$. While the product of measures $\mu \times \mu '$ is well known for combining two measures to a joint measure, the concept of a lifted product of measures $\mu \overline{\times } \mu '$ is required to do the same for combining measures that have weight on exception states. Because the formal semantics of our probabilistic programming language makes use of exception states, we always use $\overline{\times }$ to combine measures, appropriately handling exception states implicitly.

Lemma 1

For measures $\mu :\varSigma _A \rightarrow [0,\infty ]$, $\mu ' :\varSigma _B \rightarrow [0,\infty ]$, let $S \in \varSigma _A$ and $T \in \varSigma _B$. Then, $(\mu \times \mu ')(S \times T)=\mu (S) \cdot \mu '(T)$.

For $\mu :\varSigma _{\overline{A}} \rightarrow [0,\infty ]$, $\mu ' :\varSigma _{\overline{B}} \rightarrow [0,\infty ]$ and $S \in \varSigma _{\overline{A}}$, $T \in \varSigma _{\overline{B}}$, in general we have $(\mu \overline{\times } \mu ')(S \times T) \ne \mu (S) \cdot \mu '(T)$, due to interactions of exception states.

Lemma 2

$\times$ and $\overline{\times }$ for s-finite measures are associative, left- and right-distributive and preserve (sub-)probability and s-finite measures.

Lebesgue Integrals, Fubini’s Theorem for s-finite Measures. Our definition of the Lebesgue integral is based on [31]. It allows integrating functions that sometimes evaluate to $\infty$, and Lebesgue integrals evaluating to $\infty$.

Here, $(A, \varSigma _A)$ and $(B,\varSigma _B)$ are measurable spaces and $\mu :\varSigma _A \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _B \rightarrow [0,\infty ]$ are measures on A and B, respectively. Also, $E \in \varSigma _A$ and $F \in \varSigma _B$. Let $s :A \rightarrow [0, \infty )$ be a measurable function. s is a simple function if $s(x) = \sum _{i=1}^n \alpha _i [x \in A_i]$ for $A_i \in \varSigma _A$ and $\alpha _i \in \mathbb {R}$. For any simple function s, the Lebesgue integral of s over E with respect to $\mu$, denoted by $\int _{a \in E} s(a) \mu (da)$, is defined by $\sum _{i=1}^n \alpha _i\cdot \mu (A_i \cap E)$, making use of the convention $0 \cdot \infty =0$. Let $f :A \rightarrow [0,\infty ]$ be measurable but not necessarily simple. Then, the Lebesgue integral of f over E with respect to $\mu$ is defined by

$$ \int _{a \in E} f(a) \mu (da) := \sup \left\{ \int _{a \in E} s(a) \mu (da) \,\Bigg |\, s : A \rightarrow [0,\infty ) \text { is simple}, 0 \le s \le f \right\} $$

Here, the inequalities on functions are pointwise. Appendix A.2 lists some useful properties of the Lebesgue integral. Here, we only mention Fubini’s theorem, which is important because it entails a commutativity-like property of the product of measures: $(\mu \times \mu ')(S)=(\mu ' \times \mu )(\mathsf {swap}(S))$, where $\mathsf {swap}$ switches the dimensions of S: $\mathsf {swap}(S)=\{(b,a) \mid (a,b) \in S\}$. The proof of this property is straightforward, by expanding the definition of the product of measures and applying Fubini’s theorem. As we show in Sect. 5, this property is crucial for the commutativity of expressions. In the presence of exceptions, it does not hold: $(\mu \overline{\times } \mu ')(S) \ne (\mu ' \overline{\times } \mu )(\mathsf {swap}(S))$ in general.

Theorem 1

(Fubini’s theorem). For s-finite measures $\mu :\varSigma _A \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _B \rightarrow [0,\infty ]$ and any measurable function $f :A \times B \rightarrow [0, \infty ]$,

$$ \int _{a \in A} \int _{b \in B} f(a,b) \mu '(db) \mu (da) = \int _{b \in B} \int _{a \in A} f(a,b) \mu (da) \mu '(db) $$

For s-finite measures $\mu :\varSigma _{\overline{A}} \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _{\overline{B}} \rightarrow [0,\infty ]$ and any measurable function $f :A \times B \rightarrow [0, \infty ]$,

$$ \int _{a \in \overline{A}} \int _{b \in \overline{B}} \overline{f}(a,b) \mu '(db) \mu (da) = \int _{b \in \overline{B}} \int _{a \in \overline{A}} \overline{f}(a,b) \mu (da) \mu '(db) $$

(Sub-)probability Kernels, s-finite Kernels, Dirac Delta, Lebesgue Kernel, Motivation for s-finite Kernels. In the following, let $(A, \varSigma _A)$ and $(B, \varSigma _B)$ be measurable spaces. A (sub-)probability kernel with source A and target B is a function $\kappa :A \times \varSigma _B \rightarrow [0, \infty )$ such that for all $a \in A :\kappa (a, \cdot ) :\varSigma _B \rightarrow [0, \infty )$ is a (sub-)probability measure, and $\forall S \in \varSigma _B :\kappa (\cdot , S) :A \rightarrow [0,\infty )$ is measurable. $\kappa :A \times \varSigma _B \rightarrow [0, \infty ]$ is an s-finite kernel with source A and target B if $\kappa$ is a pointwise sum of sub-probability kernels $\kappa _i :A \times \varSigma _B \rightarrow [0,\infty )$, meaning $\kappa = \sum _{i \in \mathbb {N}} \kappa _i$. We denote the set of s-finite kernels with source A and target B by $A \mapsto B \subseteq A \times \varSigma _B \rightarrow [0, \infty ]$. Because we only ever deal with s-finite kernels, we often refer to them simply as kernels.

We can understand the Dirac measure as a probability kernel. For a measurable space $(A, \varSigma _A)$, the Dirac delta $\delta :A \mapsto A$ is defined by $\delta (a,S) = [a \in S]$. Note that for any a, $\delta (a,\cdot ) :\varSigma _A \rightarrow [0,\infty ]$ is the Dirac measure. We often write $\delta (a)(S)$ or $\delta _a(S)$ for $\delta (a,S)$. Note that we can also interpret $\delta :A \mapsto A$ as an s-finite kernel from $A \mapsto B$ for $A \subseteq B$. The Lebesgue kernel $\lambda ^* :A \mapsto \mathbb {R}$ is defined by $\lambda ^*(a)(S)=\lambda (S)$, where $\lambda$ is the Lebesgue measure. The definition of s-finite kernels is a lifting of the notion of s-finite measures. Note that for an s-finite kernel $\kappa$, $\kappa (a,\cdot )$ is an s-finite measure for all $a \in A$. In the context of probabilistic programming, s-finite kernels have been used before [34].

Working in the space of sub-probability kernels is inconvenient, because, for example, $\lambda ^* :\mathbb {R}\mapsto \mathbb {R}$ is not a sub-probability kernel. Even though $\lambda ^*(x)$ is $\sigma$-finite measure for all $x \in \mathbb {R}$, not all s-finite kernels induce $\sigma$-finite measures in this sense. As an example, $(\lambda ^* ;\!\lambda ^*)(x)$ is not a $\sigma$-finite measure for any $x \in \mathbb {R}$ (see Lemma 15 in Appendix A.1). We introduce ($;\!$) shortly in Definition 1.

Working in the space of s-finite kernels is convenient because s-finite kernels have many nice properties. In particular, the set of s-finite kernels $A \mapsto B$ is the smallest set that contains all sub-probability kernels with source A and target B and is closed under countable sums.

Lifting Kernels to Exception States, Removing Weight from Exception States. For kernels $\kappa :A \mapsto B$ or kernels $\kappa :A \mapsto \overline{B}$, $\kappa$ lifted to exception states $\overline{\kappa } :\overline{A} \mapsto \overline{B}$ is defined by $\overline{\kappa }(a)=\kappa (a)$ if $a \in A$ and $\overline{\kappa }(a)=\delta (a)$ if $a \notin A$. When transforming $\kappa$ into $\overline{\kappa }$, we preserve (sub-)probability and s-finite kernels.

Composing kernels, composing kernels in the presence of exception states.

Definition 1

Let $(;\!) :(A \mapsto B) \rightarrow (B \mapsto C) \rightarrow (A \mapsto C)$ be defined by $(f ;\!g)(a)(S) = \int _{b \in B} g(b)(S) \, f(a)(db)$.

Note that $f ;\!g$ intuitively corresponds to first applying f and then g. Throughout this paper, we mostly use $>\!=\!>$ instead of $(;\!)$, but we introduce $(;\!)$ because it is well-known and it is instructive to show how our definition of $>\!=\!>$ relates to $(;\!)$.

Lemma 3

$(;\!)$ is associative, left- and right-distributive, has neutral element² $\delta$ and preserves (sub-)probability and s-finite kernels.

Definition 2

Let $(>\!=\!>) :(A \mapsto \overline{B}) \rightarrow (B \mapsto \overline{C}) \rightarrow (A \mapsto \overline{C})$ be defined by $(f>\!=\!>g)(a)(S) = \int _{b \in \overline{B}} \overline{g}(b)(S) \, f(a)(db)$.

We sometimes write $f(a) \gg \!=g$ for $(f>\!=\!>g)(a)$.

Lemma 4

For $f :A \mapsto \overline{B}$ and $g :B \mapsto \overline{C}$, $a \in A$ and $S \in \varSigma _{\overline{C}}$,

$$(f>\!=\!>g)(a)(S) = (f ;\!g)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S) f(a)(\{ x \})$$

Lemma 4 shows how $>\!=\!>$ relates to $(;\!)$, by splitting $f>\!=\!>g$ into non-exceptional behavior of f (handled by $(;\!)$) and exceptional behavior of f (handled by a sum). Intuitively, if f produces an exception state $\star \in \mathcal {X}$, then g is not even evaluated. Instead, this exception is directly passed on, as indicated by $\delta (x)(S)$. If $f(a)(\mathcal {X})=0$ for all $a \in A$, or if $S \cap \mathcal {X}= \emptyset$, then the definitions are equivalent in the sense that $(f ;\!g)(a)(S)=(f>\!=\!>g)(a)(S)$. The difference between $>\!=\!>$ and $(;\!)$ is the treatment of exception states produced by f. Note that technically, the target $\overline{B}$ of $f :A \mapsto \overline{B}$ does not match the source B of $g :B \mapsto \overline{C}$. Therefore, to formally interpret $f ;\!g$, we silently restrict the domain of f to $A \times \varSigma _B$.

Lemma 5

$>\!=\!>$ is associative, left-distributive (but not right-distributive), has neutral element $\delta$ and preserves (sub-)probability and s-finite kernels.

Product of Kernels, Product of Kernels in the Presence of Exception States. For s-finite kernels $\kappa :A \mapsto B$, $\kappa ' :A \mapsto C$, we define the product of kernels, denoted by $\kappa \times \kappa ' :A \mapsto B \times C$, as $(\kappa \times \kappa ')(a)(S) = (\kappa (a) \times \kappa '(a))(S)$. For s-finite kernels $\kappa :A \mapsto \overline{B}$ and $\kappa ' :A \mapsto \overline{C}$, we define the lifted product of kernels, denoted by $\kappa \overline{\times } \kappa ' :A \mapsto \overline{B \times C}$, as $(\kappa \overline{\times } \kappa ')(a)(S) = (\kappa (a) \overline{\times } \kappa '(a))(S)$. $\times$ and $\overline{\times }$ allow us to combine kernels to a joint kernel. Essentially, this definition reduces the product of kernels to the product of measures.

Lemma 6

$\times$ and $\overline{\times }$ for kernels preserve (sub-)probability and s-finite kernels, are associative, left- and right-distributive.

Binding Conventions. To avoid too many parentheses, we make use of some binding conventions, ordering (in decreasing binding strength) $\overline{\times }, \times , ;\!,>\!=\!>, +$.

Summary. The most important concepts introduced in this section are exception states, records, Lebesgue integration, Fubini’s theorem and (s-finite) kernels.

4 A Probabilistic Language and Its Semantics

We now describe our probabilistic programming language, the typing rules and the denotational semantics of our language.

4.1 Syntax

Let $\mathbb {V}:= \mathbb {Q}\cup \{ \pi , e \} \subseteq \mathbb {R}$ be a (countable) set of constants expressible in our programs. Let $i, n \in \mathbb {N}$, $r \in \mathbb {V}$, $x \in Vars$, $\ominus$ a generic unary operator (e.g., − inverts the sign of a value, ! is logical negation mapping 0 to 1 and all other numbers to 0, $\lfloor \cdot \rfloor$ and $\lceil \cdot \rceil$ round down and up respectively), $\oplus$ a generic binary operator (e.g., $+$, −, $*$,  / , ${}^\wedge$ for addition, subtraction, multiplication, division and exponentiation,  &&, || for logical conjunction and disjunction, $=,\ne ,<,\le ,>,\ge$ to compare values). Let $f :A \rightarrow \mathbb {R}\rightarrow [0,\infty )$ be a measurable function that maps $a \in A$ to a probability density function. We check if f is measurable by uncurrying f to $f :A \times \mathbb {R}\rightarrow [0,\infty )$. Fig. 2 shows the syntax of our language.

Fig. 2.

The syntax of our probabilistic language.

Our expressions capture () (the only element of $\mathbb {1}$), r (real numbers), x (variables), $(e_1, \dots , e_n)$ (tuples), e[i] (accessing elements of tuples for $i \in \mathbb {N}$), $\ominus e$ (unary operators), $e_1 \oplus e_2$ (binary operators), $e_1[e_2]$ (accessing array elements), $e_1[e_2 \mapsto e_3]$ (updating array elements), ${{\mathbf {\mathtt{{array}}}}}\, \,(e_1,e_2)$ (creating array of length $e_1$ containing $e_2$ at every index) and F(e) (evaluating function F on argument e). To handle functions $F(e_1,\dots ,e_n)$ with multiple arguments, we interpret $(e_1,\dots ,e_n)$ as a tuple and apply F to that tuple.

Our functions express $\lambda x. \{ P; {{\mathbf {\mathtt{{return }}}}}\, \, e; \}$ (function taking argument x running P on x and returning e), ${{\mathbf {\mathtt{{flip}}}}}\, (e)$ (random choice from $\{0,1\}$, 1 with probability e), ${{\mathbf {\mathtt{{uniform}}}}}\, (e_1,e_2)$ (continuous uniform distribution between $e_1$ and $e_2$) and ${{\mathbf {\mathtt{{sampleFrom}}}}}\, _f(e)$ (sample value distributed according to probability density function f(e)). An example for f is the density of the exponential distribution, indexed with rate $\lambda$. Formally, $f :(0,\infty ) \rightarrow \mathbb {R}\rightarrow [0,\infty )$ is defined by $f(\lambda )(x)=\lambda e^{-\lambda x}$ if $x \ge 0$ and $f(\lambda )(x)=0$ otherwise. Often, f is partial (e.g., $\lambda \le 0$ is not allowed). Intuitively, arguments outside the allowed range of f produce the error state $\bot$.

Our statements express ${{\mathbf {\mathtt{{skip}}}}}\,$ (no operation), $x := e$ (assigning to a fresh variable), $x = e$ (assigning to an existing variable), $P_1; P_2$ (sequential composition of programs), ${{\mathbf {\mathtt{{if }}}}}\, e \; \{P_1\} {{\mathbf {\mathtt{{ else }}}}}\, \{P_2\}\,$ (if-then-else), $\{P\}$ (static scoping), ${{\mathbf {\mathtt{{assert}}}}}\, (e)$ (asserting that an expression evaluates to true, assertion failure results in $\bot$), ${{\mathbf {\mathtt{{observe}}}}}\, (e)$ (observing that an expression evaluates to true, observation failure results in ) and ${{\mathbf {\mathtt{{while }}}}}\, e \; \{P\}\,$ (while loops, non-termination results in $\circlearrowleft$). We additionally introduce syntactic sugar $e_1[e_2] = e_3$ for $e_1 = e_1[e_2 \mapsto e_3]$, ${{\mathbf {\mathtt{{if }}}}}\, (e) \; \{ P \}$ for ${{\mathbf {\mathtt{{if }}}}}\, e \; \{P\} {{\mathbf {\mathtt{{ else }}}}}\, \{{{\mathbf {\mathtt{{skip}}}}}\, \}\,$ and $\texttt {func}\,(e_2)$ for $\lambda x. \{P; {{\mathbf {\mathtt{{return }}}}}\, \, e_1;\}(e_2)$ (using the name $\texttt {func}\,$ for the function with argument x and body $\{ P; {{\mathbf {\mathtt{{return }}}}}\, \, e_1 \}$).

4.2 Typing Judgments

Let $n \in \mathbb {N}$. We define types by the following grammar in BNF, where $\tau []$ denotes arrays over type $\tau$. We sometimes write $\prod _{i=1}^n \tau _i$ for the product type $\tau _1 \times \cdots \times \tau _n$.

$$ \tau {:}{:}= \mathbb {1}\mid \mathbb {R}\mid \tau [] \mid \tau _1 \times \cdots \times \tau _n $$

Note that we also use the type $\tau _1 \mapsto \tau _2$ of kernels with source $\tau _1$ and target $\tau _2$, but we do not list it here to avoid higher-order functions (discussed in Sect. 4.5).

Fig. 3.

The typing rules for expressions and functions in our language

Fig. 4.

The typing rules for statements

Formally, a context $\varGamma$ is a set $\{ x_i :\tau _i \}_{i \in [n]}$ that assigns a type $\tau _i$ to each variable $x_i \in Vars$. In slight abuse of notation, we sometimes write $x \in \varGamma$ if there is a type $\tau$ with $x :\tau \in \varGamma$. We also write $\varGamma , x :\tau$ for $\varGamma \cup \{ x :\tau \}$ (where $x \notin \varGamma$) and $\varGamma ,\varGamma '$ for $\varGamma \cup \varGamma '$ (where $\varGamma$ and $\varGamma '$ have no common variables).

The rules in Figs. 3 and 4 allow deriving the type of expressions, functions and statements. To state that an expression e is of type $\tau$ under a context $\varGamma$, we write $\varGamma \vdash e :\tau$. Likewise, $\vdash F :\tau \mapsto \tau '$ indicates that F is a kernel from $\tau$ to $\tau '$. Finally, states that a context $\varGamma$ is transformed to $\varGamma '$ by a statement P. For ${{\mathbf {\mathtt{{sampleFrom}}}}}\, _f$, we intuitively want f to map values from $\tau$ to probability density functions. To allow f to be partial, i.e., to be undefined for some values from $\tau$, we use $A \in \varSigma _\tau$ (and hence $A \subseteq [\![\tau ]\!]$) as the domain of f (see Sect. 4.3).

4.3 Semantics

Semantic Domains. We assign to each type $\tau$ a set $[\![\tau ]\!]$ together with an implicit $\sigma$-algebra $\varSigma _{\tau }$ on that set. Additionally, we assign a set $[\![\varGamma ]\!]$ to each context $\varGamma = \{ x_i :\tau _i \}_{i \in [n]}$. Concretely, we have $[\![\mathbb {1}]\!]= \mathbb {1}:= \{ () \}$ with $\varSigma _{\mathbb {1}} = \left\{ \emptyset , () \right\}$, $[\![\mathbb {R}]\!]= \mathbb {R}$ and $\varSigma _\mathbb {R}= \mathcal {B}$. The remaining semantic domains are outlined in Fig. 5.

Fig. 5.

Semantic domains for types

Expressions. Fig. 6 assigns to each expression e typed by $\varGamma \vdash e :\tau$ a probability kernel $[\![e ]\!]_{\tau } :[\![\varGamma ]\!]\mapsto \overline{[\![\tau ]\!]}$. When $\tau$ is irrelevant or clear from the context, we may drop it and write $[\![e ]\!]$. The formal interpretation of $[\![\varGamma ]\!]\mapsto \overline{[\![\tau ]\!]}$ is explained in Sect. 3.³ Note that Fig. 6 is incomplete, but extending it is straightforward. When we need to evaluate multiple terms (as in $(e_1, \dots , e_n)$), we combine the results using $\overline{\times }$. This makes sure that in the presence of exceptions, the first exception that occurs will have priority over later exceptions. In addition, deterministic functions (like $x+y$) are lifted to probabilistic functions by the Dirac delta (e.g. $\delta (x+y)$) and incomplete functions (like x/y) are lifted to complete functions via the explicit error state $\bot$.

Fig. 6.

The semantics of expressions. v!n stands for the n-tuple $(v,\dots ,v)$. t[i] stands for the i-th element (0-indexed) of the tuple t and $t[i \mapsto v]$ is the tuple t, where the i-th element is replaced by v. |t| is the length of a tuple t. $\sigma$ stands for a program state over all variables in some $\varGamma$, with $\sigma \in [\![\varGamma ]\!]$.

Fig. 7 assigns to each function F typed by $\vdash F :\tau _1 \mapsto \tau _2$ a probability kernel $[\![F ]\!]_{\tau _1 \mapsto \tau _2} :[\![\tau _1 ]\!]\mapsto \overline{[\![\tau _2 ]\!]}$. In the semantics of ${{\mathbf {\mathtt{{flip}}}}}\,$, $\delta (1) :\varSigma _{\overline{\mathbb {R}}} \rightarrow [0,\infty ]$ is a measure on $\overline{\mathbb {R}}$, and $p \cdot \delta (1)$ rescales this measure pointwise. Similarly, the sum $p \cdot \delta (1)+(1-p) \cdot \delta (0)$ is also meant pointwise, resulting in a measure on $\overline{\mathbb {R}}$. Finally, $\lambda p.\,p \cdot \delta (1)+(1-p) \cdot \delta (0)$ is a kernel with source [0, 1] and target $\overline{\mathbb {R}}$. For ${{\mathbf {\mathtt{{sampleFrom}}}}}\, _f(e)$, remember that $f(p)(\cdot )$ is a probability density function.

Fig. 7.

The semantics of functions.

Fig. 8.

The semantics of programs in our probabilistic language. Here, $\sigma [x \mapsto v]$ results in $\sigma$ with the value stored under x updated to v. $\sigma '(\varGamma )$ selects only those variables from $\sigma '$ that occur in $\varGamma$, meaning $\{ x_i \mapsto v_i\}_{i \in \mathcal {I}}(\{ x_i :\tau _i\}_{i \in \mathcal {I}'})=\{ x_i \mapsto v_i\}_{i \in \mathcal {I} \cap \mathcal {I}'}$.

Statements. Fig. 8 assigns to each statement P with a probability kernel $[\![P ]\!]:[\![\varGamma ]\!]\mapsto \overline{[\![\varGamma ' ]\!]}$. Note the use of $\overline{\times }$ in $\delta \overline{\times } [\![e ]\!]$, which allows evaluating e while keeping the state $\sigma$ in which e is being evaluated. Intuitively, if evaluating e results in an exception from $\mathcal {X}$, the previous state $\sigma$ is irrelevant, and the result of $\delta \overline{\times } [\![e ]\!]$ will be that exception from $\mathcal {X}$.

While Loop. To define the semantics of the while loop ${{\mathbf {\mathtt{{while }}}}}\, e \; \{P\}\,$, we introduce a kernel transformer that transforms the semantics for n runs of the loop to the semantics for $n+1$ runs of the loop. Concretely,

This semantics first evaluates e, while keeping the program state around using $\delta$. If e evaluates to 0, the while loop terminates and we return the current program state $\sigma$. If e does not evaluate to 0, we run the loop body P and feed the result to the next iteration of the loop, using $\kappa$.

We can then define the semantics of ${{\mathbf {\mathtt{{while }}}}}\, e \; \{P\}\,$ using a special fixed point operator $\mathsf {fix}:((A \mapsto \overline{A}) \rightarrow (A \mapsto \overline{A})) \rightarrow (A \mapsto \overline{A})$, defined by the pointwise limit $\mathsf {fix}(\varDelta ) = \lim _{n \rightarrow \infty } \varDelta ^n(\pmb {\circlearrowleft })$, where $\pmb {\circlearrowleft }:= \lambda \sigma .\,\delta (\circlearrowleft )$ and $\varDelta ^n$ denotes the n-fold composition of $\varDelta$. $\varDelta ^n(\pmb {\circlearrowleft })$ puts all runs of the while loop that do not terminate within n steps into the state $\circlearrowleft$. In the limit, $\circlearrowleft$ only has weight on those runs of the loop that never terminate. $\mathsf {fix}(\varDelta )$ is only defined if its pointwise limit exists. Making use of $\mathsf {fix}$, we can define the semantics of the while loop as follows:

Lemma 7

For $\varDelta$ as in the semantics of the while loop, and for each $\sigma$ and each S, the limit $\lim _{n \rightarrow \infty } \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S)$ exists.

Lemma 7 holds because increasing n may only shift probability mass from $\circlearrowleft$ to other states (we provide a formal proof in Appendix B). Kozen shows a different way of defining the semantics of the while loop [23], using least fixed points. Lemma 8 describes the relation of the semantics of our while loop to the semantics of the while loop of [23]. For more details on the formal interpretation of Lemma 8 and for its proof, see Appendix B.

Lemma 8

In the absence of exception states, and using sub-probability kernels instead of distribution transformers, the definition of the semantics of the while loop from [23] is equivalent to ours.

Theorem 2

The semantics of each expression $[\![e ]\!]$ and statement $[\![P ]\!]$ is indeed a probability kernel.

Proof

The proof proceeds by induction. Some lemmas that are crucial for the proof are listed in Appendix C. Conveniently, most functions that come up in our definition are continuous (like $a+b$) or continuous except on some countable subset (like $\frac{a}{b}$) and thus measurable.

4.4 Recursion

To extend our language with recursion, we apply the same ideas as for the while loop. Given the source code of a function F that uses recursion, we define its semantics in terms of a kernel transformer $[\![F ]\!]^\mathsf {trans}$. This kernel transformer takes semantics for F up to a recursion depth of n and returns semantics for F up to recursion depth $n+1$. Formally, $[\![F ]\!]^\mathsf {trans}(\kappa )$ follows the usual semantics, but uses $\kappa$ as the semantics for recursive calls to F (we will provide an example shortly). Finally, we define the semantics of F by $[\![F ]\!]:= \mathsf {fix}\Big ( [\![F ]\!]^\mathsf {trans}\Big )$. Just as for the while loop, $\mathsf {fix}\Big ( [\![F ]\!]^\mathsf {trans}\Big )$ is well-defined because stepping from recursion depth n to $n+1$ can only shift probability mass from $\circlearrowleft$ to other states. We note that we could generalize our approach to mutual recursion.

To demonstrate how we define the kernel transformer, consider the recursive implementation of the geometric distribution in Listing 11 (to simplify presentation, Listing 11 uses early return). Given semantics $\kappa$ for $\texttt {geom}:\mathbb {1} \mapsto \mathbb {R}$ up to recursion depth n, we can define the semantics of $\texttt {geom}$ up to recursion depth $n+1$, as illustrated in Fig. 9.

Fig. 9.

Kernel transformer $[\![\texttt {geom} ]\!]^\mathsf {trans}(\kappa )$ for $\texttt {geom}$ given in Listing 11.

4.5 Higher-Order Functions

Our language cannot express higher-order functions. When trying to give semantics to higher-order probabilistic programs, an important step is to define a $\sigma$-algebra on the set of functions from real numbers to real numbers. Unfortunately, no matter which $\sigma$-algebra is picked, function evaluation (i.e. the function that takes f and x as arguments and returns f(x)) is not measurable [1]. This is a known limitation that previous work has looked into (e.g. [35] address it by restricting the set of functions to those expressible by their source code).

A promising recent approach is replacing measurable spaces by quasi-Borel spaces [16]. This allows expressing higher-order functions, at the price of replacing the well-known and well-understood measurable spaces by a new concept.

4.6 Non-determinism

To extend our language with non-determinism, we may define the semantics of expressions, functions and statements in terms of sets of kernels. For an expression e typed by $\varGamma \vdash e:\tau$, this means that $[\![e ]\!]_\tau \in \mathcal {P}\left( [\![\varGamma ]\!]\mapsto [\![\tau ]\!]\right)$, where $\mathcal {P}\left( S\right)$ denotes the power set of S. Lifting our semantics to non-determinism is mostly straightforward, except for loops. There, $[\![{{\mathbf {\mathtt{{while }}}}}\, e \; \{P\}\, ]\!]$ contains all kernels of the form $\lim _{n \rightarrow \infty } (\varDelta _1 \circ \cdots \circ \varDelta _n)(\pmb {\circlearrowleft })$, where . Previous work has studied non-determinism in more detail, see e.g. [21, 22].

5 Properties of Semantics

We now investigate two properties of our semantics: commutativity and associativity. These are useful in practice, e.g. because they enable rewriting programs to a form that allows for more efficient inference [5].

In this section, we write $e_1 \simeq e_2$ when expressions $e_1$ and $e_2$ are equivalent (i.e. when $[\![e_1 ]\!]= [\![e_2 ]\!]$). Analogously, we write $P_1 \simeq P_2$ for $[\![P_1 ]\!]= [\![P_2 ]\!]$.

5.1 Commutativity

In the presence of exception states, our language cannot guarantee commutativity of expressions such as $e_1 + e_2$. This is not surprising, as in our semantics the first exception bypasses all later exceptions.

Lemma 9

For function $F()\{ {{\mathbf {\mathtt{{while }}}}}\, 1 \; \{{{\mathbf {\mathtt{{skip}}}}}\, \}\,; {{\mathbf {\mathtt{{return }}}}}\, \, 0 \}$,

$$ \frac{1}{0} + F() \not \simeq F() + \frac{1}{0} $$

Formally, this is because if we evaluate $\frac{1}{0}$ first, we only have weight on $\bot$. If instead, we evaluate F() first, we only have weight on $\circlearrowleft$, by an analogous calculation. A more detailed proof is included in Appendix D.

However, the only reason for non-commutativity is the presence of exceptions. Assuming that $e_1$ and $e_2$ cannot produce exceptions, we obtain commutativity:

Lemma 10

If $[\![e_1 ]\!](\sigma )(\mathcal {X})=[\![e_2 ]\!](\sigma )(\mathcal {X})=0$ for all $\sigma$, then $e_1 \oplus e_2 \simeq e_2 \oplus e_1$, for any commutative operator $\oplus$.

The proof of Lemma 10 (provided in Appendix D) relies on the absence of exceptions and Fubini’s Theorem. This commutativity result is in line with the results from [34], which proves commutativity in the absence of exceptions.

In the analogous situation for statements, we cannot assume commutativity $P_1;P_2 \simeq P_2;P_1$, even if there is no dataflow from $P_1$ to $P_2$. We already illustrated this in Listing 10, where swapping two lines changes the program semantics. However, in the absence of exceptions and dataflow from $P_1$ to $P_2$, we can guarantee $P_1;P_2 \simeq P_2;P_1$.

5.2 Associativity

A careful reader might suspect that since commutativity does not always hold in the presence of exceptions, a similar situation might arise for associativity of some expressions. As an example, can we guarantee $e_1+(e_2+e_3)\simeq (e_1+e_2)+e_3$, even in the presence of exceptions? The answer is yes, intuitively because exceptions can only change the behavior of a program if the order of their occurrence is changed. This is not the case for associativity. Formally, we derive the following:

Lemma 11

$e_1 \oplus (e_2 \oplus e_3)\simeq (e_1 \oplus e_2) \oplus e_3$, for any associative operator $\oplus$.

We include notes on the proof of Lemma 11 in Appendix D, mainly relying on the associativity of $\overline{\times }$ (Lemma 6). Likewise, sequential composition is associative: $(P_1; P_2); P_3 \simeq P_1; (P_2; P_3)$. This is due to the associativity of $>\!=\!>$ (Lemma 5).

5.3 Adding the score  Primitive

Some languages include the primitive ${{\mathbf {\mathtt{{score}}}}}\,$, which allows to increase or decrease the probability of a certain event (or trace) [34, 35].

Listing 12 shows an example program using ${{\mathbf {\mathtt{{score}}}}}\,$. Without normalization, it returns 0 with probability $\frac{1}{2}$ and 1 with “probability” $\frac{1}{2} \cdot 2=1$. After normalization, it returns 0 with probability $\frac{1}{3}$ and 1 with probability $\frac{2}{3}$. Because ${{\mathbf {\mathtt{{score}}}}}\,$ allows decreasing the probability of a specific event, it renders ${{\mathbf {\mathtt{{observe}}}}}\,$ unnecessary. In general, we can replace ${{\mathbf {\mathtt{{observe}}}}}\, (e)$ by ${{\mathbf {\mathtt{{score}}}}}\, (e \ne 0)$. However, performing this replacement means losing the explicit knowledge of the weight on .

${{\mathbf {\mathtt{{score}}}}}\,$ can be useful to modify the shape of a given distribution. For example, Listing 13 turns the distribution of x, which is a Gaussian distribution, into the Lebesgue measure $\lambda$, by multiplying the density of x by its inverse. Hence, the density of x at any location is 1. Note that the distribution over x cannot be described by a probability measure, because e.g. the “probability” that x lies in the interval [0, 2] is 2.

Unfortunately, termination in the presence of ${{\mathbf {\mathtt{{score}}}}}\,$ is not well-defined, as illustrated in Listing 14. In this program, the only non-terminating trace keeps changing its weight, switching between 1 and 2. In the limit, it is impossible to determine the weight of non-termination.

Hence, allowing the use of the ${{\mathbf {\mathtt{{score}}}}}\,$ primitive only makes sense after abolishing the tracking of non-termination ($\circlearrowleft$), which can be achieved by only measuring sets that do not contain non-termination. Formally, this means restricting the semantics of expressions e typed by $\varGamma \vdash e: \tau$ to $[\![e ]\!]_\tau :\varGamma \mapsto \left( \overline{[\![\tau ]\!]} - \{ \circlearrowleft \} \right)$. Intuitively, abolishing non-termination means that we ignore non-terminating runs (these result in weight on non-termination). After doing this, we can give well-defined semantics to the ${{\mathbf {\mathtt{{score}}}}}\,$ primitive.

The typing rule and semantics of ${{\mathbf {\mathtt{{score}}}}}\,$ are:

After including ${{\mathbf {\mathtt{{score}}}}}\,$ into our language, the semantics of the language can no longer be expressed in terms of probability kernels as stated in Theorem 2, because the probability of any event can be inflated beyond 1. Instead, the semantics must be expressed in terms of s-finite kernels.

Theorem 3

After adding the ${{\mathbf {\mathtt{{score}}}}}\,$ primitive and abolishing non-termination, the semantics of each expression $[\![e ]\!]$ and statement $[\![P ]\!]$ is an s-finite kernel.

Proof

As for Theorem 2, the proof proceeds by induction. Most parts of the proof are analogous (e.g. $>\!=\!>$ preserves s-finite kernels instead of probability kernels). For while loops, the limit still exists (Lemma 7 still holds), but it is not bounded from above anymore. The limit indeed corresponds to an s-finite kernel because the limit of strictly increasing s-finite kernels is an s-finite kernel.

In the presence of ${{\mathbf {\mathtt{{score}}}}}\,$, we can still talk about the interaction of different exceptions, assuming that we do track different types of exceptions (e.g. division by zero and out of bounds access of arrays). Then, we keep the commutativity and associativity properties studied in the previous sections, because these still hold for s-finite kernels.

Listing 15 shows an interaction of ${{\mathbf {\mathtt{{score}}}}}\,$ with ${{\mathbf {\mathtt{{assert}}}}}\,$. As one would expect, our semantics will assign weight 2 to $\bot$ in this case. If the two statements are switched, our semantics will ignore ${{\mathbf {\mathtt{{score}}}}}\, (2)$ and assign weight 1 to $\bot$. Hence again, commutativity does not hold.

Listing 16 shows a program that keeps increasing the probability of an error. In every loop iteration, there is a “probability” of 1 of running into an error. Overall, Listing 16 results in weight $\infty$ on state $\bot$.

Table 3. Comparison of existing semantics to ours. When adding ${{\mathbf {\mathtt{{score}}}}}\,$ to our language (Sect. 5.3), our semantics use s-finite kernels (not probability kernels).

6 Related Work

Kozen provides classic semantics to probabilistic programs [23]. We follow his main ideas, but deviate in some aspects in order to introduce additional features or to make our presentation cleaner. The semantics by Hur et al. [19] is heavily based on [23], so we do not go into more detail here. Table 3 summarizes the comparison of our approach to that of others.

Kernels. Like our work, most modern approaches use kernels (i.e., functions from values to distributions) to provide semantics to probabilistic programs [4, 24, 33, 34]. Borgström et al. [4] use sub-probability kernels on (symbolic) expressions. Staton [34] uses s-finite kernels to capture the semantics of the ${{\mathbf {\mathtt{{score}}}}}\,$ primitive (when we discuss ${{\mathbf {\mathtt{{score}}}}}\,$ in Sect. 5.3, we do the same).

In the classic semantics of [23], Kozen uses distribution transformers (i.e., functions from distributions to distributions). For later work [24], Kozen also switches to sub-probability kernels, which has the advantage of avoiding redundancies. A different approach uses weakest precondition to define the semantics, as in [28]. Staton et al. [35] use a different concept of measurable functions $A \rightarrow P(\mathbb {R}_{\ge 0} \times B)$ (where P(S) denotes the set of all probability measures on S).

Typing. Some probabilistic languages are untyped [4, 28], while others are limited to just a single type: $\mathbb {R}^n$ [23, 24] or $\bigcup _{i=1}^\infty \mathbb {N}^i \cup \mathbb {N}^\infty$ [33]. Some languages provide more interesting types including sum types, distribution types and tuples [34, 35]. We allow tuples and array types, and we could easily account for sum types.

Loops. Because the semantics of while loops is not always straightforward, some languages avoid while loops and recursion altogether [35]. Borgström et al. handle recursion instead of while loops, defining the semantics in terms of a fixed point [4]. Many languages handle while loops by least fixed points [23, 24, 28, 33]. Staton defines while loops in terms of the counting measure [34], which is similar to defining them by a fixed point. We define the semantics of while loops in terms of a fixed point, which avoids the need to prove the least fixed point exists (still, the classic while loop semantics of [23] and our formulation are equivalent).

Most languages do not explicitly track non-termination, but lose probability weight by non-termination [4, 23, 24, 34]. This missing weight can be used to identify the probability of non-termination, but only if other exceptions (such as ${{\mathbf {\mathtt{{fail}}}}}\,$ in [24] or observation failure in [4]) do not also result in missing weight. The semantics of [33] are tailored to applications in networks and lose non-terminating packet histories instead of weight (due to a particular least fixed point construction of Scott-continuous maps on algebraic and continuous directed complete partial orders). Some works define non-termination as missing weight in the weakest precondition [28]. Specifically, the semantics in [28] can also explicitly express probability of non-termination or ending up in some state (using the separate construct of a weakest liberal precondition). We model non-termination by an explicit state $\circlearrowleft$, which has the advantage that in the context of lost weight, we know what part of that lost weight is due to non-termination.

Kaminski et al. [21] investigate the run-time of probabilistic program with loops and ${{\mathbf {\mathtt{{fail}}}}}\,$ (interpreted as early termination), but without observations. In [21], non-termination corresponds to an infinite run-time.

Error States. Many languages do not consider partial functions (like fractions $\frac{a}{b}$) and thus never run into an exception state [23, 24, 33]. Olmedo et al. [28] do not consider partial functions, but support the related concept of an explicit ${{\mathbf {\mathtt{{abort}}}}}\,$. The semantics of ${{\mathbf {\mathtt{{abort}}}}}\,$ relies on missing weight in the final distribution. Some languages handle expressions whose evaluation may fail using sum types [34, 35], forcing the programmer to deal with errors explicitly (we discuss the disadvantages of this approach at Listing 6). Formally, a sum type $A+B$ is a disjoint union of the two sets A and B. Defining the semantics of an expression in terms of the sum type $A+\{ \bot \}$ allows that expression to evaluate to either a value $a \in A$ or to $\bot$. Borgström et al. [4] have a single state ${{\mathbf {\mathtt{{fail}}}}}\,$ expressing exceptions such as dynamically detected type errors (without forcing the programmer to deal with exceptions explicitly). Our semantics also uses sum types to handle exceptions, but the handling is implicit, by defining semantics in terms of $(>\!=\!>)$ (which defines how exceptions propagate in a program) instead of $(;\!)$.

Constraints. To enforce hard constraints, we use the ${{\mathbf {\mathtt{{observe}}}}}\, (e)$ statement, which puts the program into a special failure state if it does not satisfy e. We can encode soft constraints by ${{\mathbf {\mathtt{{observe}}}}}\, (e)$, where e is probabilistic (this is a general technique). Borgström et al. [4] allow both soft constraints that reduce the probability of some program traces and hard constraints whose failure leads to the error state ${{\mathbf {\mathtt{{fail}}}}}\,$. Some languages can handle generalized soft constraints: they can not only decrease the probability of certain traces using soft constraints, but also increase them, using ${{\mathbf {\mathtt{{score}}}}}\, (x)$ [34, 35]. We investigate the consequences of adding ${{\mathbf {\mathtt{{score}}}}}\,$ to our language in Sect. 5.3. Kozen [24] handles hard (and hence soft) constraints using ${{\mathbf {\mathtt{{fail}}}}}\,$ (which results in a sub-probability distribution). Some languages can handle neither hard nor soft constraints [23, 33]. Note though that the semantics of ProbNetKAT in [33] can drop certain packages, which is a similar behavior. Olmedo et al. [28] handle hard (and hence soft) constraints by a conditional weakest precondition that tracks both the probability of not failing any observation and the probability of ending in specific states. Unfortunately, this work is restricted to discrete distributions and is specifically designed to handle observation failures and non-termination. Thus, it is not obvious how to adapt the semantics if a different kind of exception is to be added.

Interaction of Different Exceptions. Most existing work handles at least some exceptions by sub-probability distributions [4, 23, 24, 33, 34]. Then, any missing weight in the final distribution must be due to exceptions. However, this leads to a conflation of all exceptions handled by sub-probability distributions (for the consequences of this, see, e.g., our discussion of Listing 8). Note that semantics based on sub-probability kernels can add more exceptions, but they will simply be conflated with all other exceptions.

Some previous work does not (exclusively) rely on sub-probability distributions. Borgström et al. [4] handle errors implicitly, but still use sub-probability kernels to handle non-termination and ${{\mathbf {\mathtt{{score}}}}}\,$. Olmedo et al. can distinguish non-termination (which is conflated with exception failure) from failing observations by introducing two separate semantic primitives (conditional weakest precondition and conditional liberal weakest precondition) [28]. Because their solution specifically addresses non-termination, it is non-trivial to generalize this treatment to more than two exception states. By using sum types, some semantics avoid interactions of errors with non-termination or constraint failures, but still cannot distinguish the latter [34, 35]. Note that semantics based on sum types can easily add more exceptions (although it is impossible to add non-termination). However, the interaction of different exceptions cannot be observed, because the programmer has to handle exceptions explicitly.

To the best of our knowledge, we are the first to give formal semantics to programs that may produce exceptions in this generality. One work investigates assertions in probabilistic programs, but explicitly disallows non-terminating loops [32]. Moreover, the semantics in [32] are operational, leaving the distribution (in terms of measure theory) of program outputs unclear. Cho et al. [8] investigate the interaction of partial programs and observe, but are restricted to discrete distributions and to only two exception states. In addition, this investigation treats these two exception states differently, making it non-trivial to extend the results to three or more exception states. Katoen et al. [22] investigate the intuitive problems when combining non-termination and observations, but restrict their discussions to discrete distributions and do not provide formal semantics. Huang [17] treats partial functions, but not different kinds of exceptions. In general, we know of no probabilistic programming language that distinguishes more than two different kinds of exceptions. Distinguishing two kinds of exceptions is simpler than three, because it is possible to handle one exception as an explicit exception state and the other one by missing weight (as e.g. in [4]).

Cousot and Monerau [9] provide a trace semantics that captures probabilistic behavior by an explicit randomness source given to the program as an argument. This allows handling non-termination by non-terminating traces. While the work does not discuss errors or observation failure, it is possible to add both. However, using an explicit randomness source has other disadvantages, already discussed by Kozen [23]. Most notably, this approach requires a distribution over the randomness source and a translation from the randomness source to random choices in the program, even though we only care about the distribution of the latter.

7 Conclusion

In this work we presented an expressive probabilistic programming language that supports important features such as mixing continuous and discrete distributions, arrays, observations, partial functions and while-loops. Unlike prior work, our semantics distinguishes non-termination, observation failures and error states. This allows us to investigate the subtle interaction of different exceptions, which is not possible for semantics that conflate different kinds of exceptions. Our investigation confirms the intuitive understanding of the interaction of exceptions presented in Sect. 2. However, it also shows that some desirable properties, like commutativity, only hold in the absence of exceptions. This situation is unavoidable, and largely analogous to the situation in deterministic languages.

Even though our semantics only distinguish three exception states, it can be trivially extended to handle any countable set of exception states. This allows for an even finer-grained distinction of e.g. division by zero, out of bounds array accesses or casting failures (in a language that allows type casting). Our semantics also allows enriching exceptions with the line number that the exception originated from (of course, this is not possible for non-termination). For an uncountable set of exception states, an extension is possible but not trivial.

Appendices

A Proofs for Preliminaries

In this section, we provide lemmas, proofs and some definitions that were left out or cut short in Sect. 3. For a more detailed introduction into measure theory, we recommend the book A crash course on the Lebesgue integral and measure theory [7].

1.1 A.1 Measures

Definition 3

Let $(A, \varSigma _A)$ be a measurable space and $\mu :\varSigma _A \rightarrow [0,\infty ]$ a measure on A.

• We call $\mu$ s-finite if $\mu$ can be written as a countable sum $\sum _{i \in \mathbb {N}} \mu _i$ of sub-probability measures $\mu _i$.

• We call $\mu$ $\sigma$-finite if $A = \bigcup _{i \in \mathbb {N}} A_i$ for $A_i \in \varSigma _A$, with $\mu (A_i)<\infty$.

• We call $\mu$ finite if $\mu (A) < \infty$.

• We call $\mu$ a sub-probability measure if $\mu (A) \le 1$.

• We call $\mu$ a probability measure if $\mu (A) = 1$.

Note that for a $\sigma$-finite measure $\mu$, $\mu (A)=\infty$ is possible, even though $\mu (A_i)<\infty$ for all i. As an example, the Lebesgue measure is $\sigma$-finite because $\mathbb {R}=\bigcup _{i \in \mathbb {N}} [-i,i]$ with $\lambda ([-i,i])=2*i$, but $\lambda (\mathbb {R})=\infty$.

Lemma 12

The following definition of s-finite measures is equivalent to our definition of s-finite measures (the difference is that the $\mu _i$s are only required to be finite):

We call $\mu :\varSigma _A \rightarrow [0,\infty ]$ an s-finite measure if it can be written as $\mu = \sum _{i \in \mathbb {N}} \mu _i$ for finite measures $\mu _i :\varSigma _A \rightarrow [0,\infty ]$.

Proof

Since any sub-probability measure is finite, one direction is trivial. For the other direction, let $\mu = \sum _{i \in \mathbb {N}} \mu _i'$ for finite measures $\mu _i'$. Obviously, $\mu \ge 0$, $\mu (\emptyset ) = 0$ and $\mu (\bigcup _{i \in \mathbb {N}} A_i) = \sum _{i \in \mathbb {N}} A_i$ for mutually disjoint $A_i \in \varSigma _A$, so $\mu$ is a measure. To show that $\mu$ can be written as a sum of sub-probability measures, let $n_i := \lceil \mu _i'(A) \rceil$. Then, $\mu = \sum _{i \in \mathbb {N}} \mu _i' = \sum _{i \in \mathbb {N}} \frac{n_i}{n_i} \mu _i' = \sum _{i \in \mathbb {N}} \sum _{j \in [n_i]} \frac{1}{n_i} \mu _i'$. We let $\mu _i := \frac{1}{n_i} \mu _i' \le 1$.

Lemma 13

Any $\sigma$-finite measure $\mu :\varSigma _A \rightarrow [0,\infty ]$ is s-finite.

Proof

Since $\mu$ is $\sigma$-finite, $A = \bigcup _{i \in \mathbb {N}} A_i$ with $A_i \in \varSigma _A$ and $\mu (A_i)<\infty$. Without loss of generality, assume that the $A_i$ form a partition of A. Then, $\mu (S) = \sum _{i \in \mathbb {N}} \mu (S \cap A_i)$, with $\mu (\cdot \cap A_i) < \infty$. Thus, $\mu$ is a countable sum of finite measures.

Definition 4

The counting measure $c :\mathcal {B} \rightarrow [0,\infty ]$ is defined by

$$c(S)={\left\{ \begin{array}{ll} |S| &{} S \text { finite} \\ \infty &{} \text {otherwise} \end{array}\right. }$$

Definition 5

The infinity measure $\mu :\mathcal {B} \rightarrow [0,\infty ]$ is defined by

$$\mu (S)={\left\{ \begin{array}{ll} 0 &{} S = \emptyset \\ \infty &{} \text {otherwise} \end{array}\right. }$$

Lemma 14

Neither the counting measure nor the infinity measure are s-finite.

Proof

For the counting measure c, assume (toward a contradiction) $c=\sum _{i \in \mathbb {N}} c_i$. We have $\mathbb {R}= \{ r \in \mathbb {R}\mid c(\{r\})> 0\} = \bigcup _{i \in \mathbb {N}} \{ r \in \mathbb {R}\mid c_i(\{r\})> 0\} = \bigcup _{i \in \mathbb {N}} \bigcup _{n \in \mathbb {N}} \{r \in \mathbb {R}\mid c_i(\{r\}) > \frac{1}{n} \}$. Because $\mathbb {R}$ is uncountable, there must be $i,n \in \mathbb {N}$ for which $S:=\{r \in \mathbb {R}\mid c_i(\{r\}) > \frac{1}{n} \}$ is uncountable. Thus for any measurable, countably infinite $S' \subseteq S$, $c_i(S')=\infty$, which means that $c_i$ is not finite. Proceed analogously for the infinity measure.

Lemma 15

The measure $\mu :\mathcal {B} \rightarrow [0,\infty ]$ with $\mu (S)={\left\{ \begin{array}{ll} 0 &{} \lambda (S) = 0 \\ \infty &{} \lambda (S) > 0 \end{array}\right\} }$ is s-finite but not $\sigma$-finite.

Proof

$\mu = \sum _{i \in \mathbb {N}} \lambda$, and $\lambda$ is s-finite, so $\mu$ is s-finite. Assume (toward a contradiction) that $\mu$ is $\sigma$-finite. Then $\mathbb {R}= \bigcup _{i \in \mathbb {N}} A_i$ with $A_i \in \mathcal {B}$ and $\mu (A_i) < \infty$. Thus, $\mu (A_i)=0$ and hence $\mu (\mathbb {R})=\mu (\bigcup _{i \in \mathbb {N}} A_i)\le \sum _{i \in \mathbb {N}} \mu (A_i)=0$, a contradiction.

Lemma 16

$$\begin{aligned} \forall S \in \varSigma _{A \times B} :(\mu \times \mu ')(S)&= \int _{a \in A} \mu '(\{ b \in B \mid (a,b) \in S \}) \mu (da) \\&= \int _{b \in B} \mu (\{ a \in A \mid (a,b) \in S \}) \mu '(db) \end{aligned}$$

$$\begin{aligned} \forall S \in \varSigma _{\overline{A \times B}} :(\mu \overline{\times } \mu ')(S)&= \int _{a \in \overline{A}} \mu '(\{ b \in \overline{B} \mid \overline{(a,b)} \in S \}) \mu (da) \\&= \int _{b \in \overline{B}} \mu (\{ a \in \overline{A} \mid \overline{(a,b)} \in S \}) \mu '(db) \end{aligned}$$

Proof

$$\begin{aligned} (\mu \times \mu ')(S)&= \int \limits _{a \in A} \int \limits _{b \in B} [(a,b) \in S] \mu '(db) \mu (da) \\&= \int \limits _{a \in A} \int \limits _{b \in B} [b \in \{ b' \in B \mid (a,b') \in S \}] \mu '(db) \mu (da) \\&= \int \limits _{a \in A} \mu '(\{ b' \in B \mid (a,b') \in S \}) \mu (da) \\ \\ (\mu \times \mu ')(S)&= \int \limits _{a \in A} \int \limits _{b \in B} [(a,b) \in S] \mu '(db) \mu (da) \\&= \int \limits _{b \in B} \int \limits _{a \in A} [(a,b) \in S] \mu (da) \mu '(db)&\text {Fubini} \\&= \dots \\&= \int \limits _{b \in B} \mu (\{ a' \in A \mid (a',b) \in S \}) \mu '(db) \end{aligned}$$

In the second line, we have used that $(a,b) \in S \iff b \in \{ b' \in B \mid (a,b') \in S \}$. The proof works analogously for $\overline{\times }$.

Lemma 17

Let $\delta :A \mapsto A$, $\kappa :A \mapsto B$. Then,

$$ (\delta \overline{\times } \kappa )(a)(S) = \kappa (a)(\{ b \in \overline{B} \mid \overline{(a,b)} \in S\}) $$

Proof

$$\begin{aligned} (\delta \overline{\times } \kappa )(a)(S)&= \int _{b \in \overline{B}} \delta (a)(\{ a' \in A \mid \overline{(a',b)} \in S \}) \kappa (a)(db)&\text{ Lemma } \text{16 } \\&= \int _{b \in \overline{B}} [\overline{(a,b)} \in S] \kappa (a)(db) \\&= \kappa (a)(\{ b \in \overline{B} \mid \overline{(a,b)} \in S \}) \end{aligned}$$

Lemma 1

For measures $\mu :\varSigma _A \rightarrow [0,\infty ]$, $\mu ' :\varSigma _B \rightarrow [0,\infty ]$, let $S \in \varSigma _A$ and $T \in \varSigma _B$. Then, $(\mu \times \mu ')(S \times T)=\mu (S) \cdot \mu '(T)$.

Proof

$$\begin{aligned} (\mu \times \mu ')(S \times T)&= \int _{a \in A} \mu '(\{b \in B \mid (a,b) \in S \times T\}) \mu (da)&\text{ Lemma } \text{16 } \\&= \int _{a \in A} \mu '\left( {\left\{ \begin{array}{ll} T &{} a \in S \\ \emptyset &{} \text {otherwise} \end{array}\right\} }\right) \mu (da) \\&= \int _{a \in S} \mu '(T) \mu (da) \\&= \mu (S)*\mu '(T) \end{aligned}$$

Lemma 2

$\times$ and $\overline{\times }$ for s-finite measures are associative, left- and right-distributive and preserve (sub-)probability and s-finite measures.

Proof

Remember that $(\mu \times \mu ')(S) = \int _{a \in A} \int _{b \in B} [(a,b) \in S] \mu '(db) \mu (da)$ and that $(\mu \overline{\times } \mu ')(S) = \int _{a \in \overline{A}} \int _{b \in \overline{B}} [\overline{(a,b)} \in S] \mu '(db) \mu (da)$. Preservation of (sub-)probability measures is trivial. Distributivity and preservation of s-finite measures are easily established by properties of the Lebesgue integral in Lemma 19.

For associativity, let $\mu :\varSigma _A \rightarrow [0, \infty ]$, $\mu :\varSigma _B \rightarrow [0, \infty ]$ and $\mu :\varSigma _C \rightarrow [0, \infty ]$.

$$\begin{aligned}&((\mu \times \mu ') \times \mu '')(S) \\ =&\int \limits _{c \in C} (\mu \times \mu ')(\{ t \in A \times B \mid (t,c) \in S \}) \mu ''(dc)&\text{ Lemma } \text{16 } \\ =&\int \limits _{c \in C} \int \limits _{a \in A} \int \limits _{b \in B} [(a,b) \in \{ t \in A \times B \mid (t,c) \in S \}] \mu '(db) \mu (da) \mu ''(dc) \\ =&\int \limits _{c \in C} \int \limits _{a \in A} \int \limits _{b \in B} [(a,b,c) \in S] \mu '(db) \mu (da) \mu ''(dc) \\ =&\int \limits _{a \in A} \int \limits _{b \in B} \int \limits _{c \in C} [(a,b,c) \in S] \mu ''(dc) \mu '(db) \mu (da)&\text {Fubini} \\ =&\int \limits _{a \in A} \int \limits _{b \in B} \int \limits _{c \in C} [(b,c) \in \{ t \in B \times C \mid (a,t) \in S\}] \mu ''(dc) \mu '(db) \mu (da) \\ =&\int \limits _{a \in A} (\mu ' \times \mu '')(\{ t \in B \times C \mid (a,t) \in S\}) \mu (da) \\ =&(\mu \times (\mu ' \times \mu ''))(S) \mu (da)&\text{ Lemma } \text{16 } \end{aligned}$$

The proof proceeds analogously for $\overline{\times }$.

Lemma 18

Let $(A,\varSigma _A)$ and $(B,\varSigma _B)$ be measurable spaces. Consider measures $\mu ,\mu _1,\mu _2 :\varSigma _A \rightarrow [0,\infty ]$ and $\nu ,\nu _1,\nu _2 :\varSigma _B \rightarrow [0,\infty ]$. We assume that $\nu _1 \le \nu _2$ and $\mu _1 \le \mu _2$ hold pointwise. Then,

$$\begin{aligned} \mu \overline{\times } \nu _1&\le \mu \overline{\times } \nu _2 \\ \mu _1 \overline{\times } \nu&\le \mu _2 \overline{\times } \nu \end{aligned}$$

Proof

Let $S \in \varSigma _{A \times B}$ and $\nu _1 \le \nu _2$. Then, we have

$$\begin{aligned}&\nu _1 \le \nu _2 \\ \implies&\underbrace{\int _{b \in \overline{B}} [\overline{(a,b)} \in S] \nu _1(db)}_{=:f(a)} \le \underbrace{\int _{b \in \overline{B}} [\overline{(a,b)} \in S] \nu _2(db)}_{=:g(a)}&\text{ Lemma } \text{19 } \\ \implies&\int _{a \in \overline{A}} f(a) \mu (da) \le \int _{a \in \overline{A}} g(a) \mu (da)&\text{ Lemma } \text{19 } \\ \implies&(\mu \overline{\times } \nu _1)(S) \le (\mu \overline{\times } \nu _2)(S) \end{aligned}$$

The proof for $\mu _1 \overline{\times } \nu \le \mu _2 \overline{\times } \nu$ is similar.

1.2 A.2 Lebesgue Integral

Lemma 19

Let $(A,\varSigma _A)$ and $(B,\varSigma _B)$ be measurable spaces, $E \in \varSigma _A$ and $E' \in \varSigma _B$ measurable sets, $f,f_i,g :A \rightarrow \mathbb {R}$ and $h :A \times B \rightarrow \mathbb {R}$ measurable functions, $\mu ,\mu _i,\nu :\varSigma _A \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _B \rightarrow [0,\infty ]$ measures.

$$\begin{aligned} \int \limits _{a \in E} f(a) \mu (da) \in&\, [0,\infty ] \\ 0 \le f \le g \le \infty \implies&\int \limits _{a \in E} f(a) \mu (da) \le \int \limits _{a \in E} g(a) \mu (da) \\ \mu \le \nu \implies&\int \limits _{a \in E} f(a) \mu (da) \le \int \limits _{a \in E} f(a) \nu (da) \\ \sum _{n=1}^\infty \int \limits _{a \in E} f_n(a) \mu (da) =&\int \limits _{a \in E} \sum _{n=1}^\infty f_n(a) \mu (da) \\ \int \limits _{a \in E} \int \limits _{b \in E'} f(a,b) \mu '(db) \mu (da) =&\int \limits _{b \in E'} \int \limits _{a \in E} f(a,b) \mu '(da) \mu (db)&\mu , \mu ' \sigma \text {-finite} \\ \int \limits _{a \in E} f(a) \left( \sum _{n=1}^\infty \mu _i\right) (da) =&\sum _{n=1}^\infty \int \limits _{a \in E} f(a) \mu _i(da) \\ \int \limits _{a \in E} f(a) \delta (x)(da) =&f(x)&x \in E \end{aligned}$$

Finally, if $f_1 \le f_2 \le \cdots \le \infty$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty } \int \limits _{a \in E} f_n(a) \mu (da) =&\int \limits _{a \in E} \lim _{n \rightarrow \infty } f_n(a) \mu (da) \end{aligned}$$

Proof

The following properties can be proven for simple functions and limits of simple functions (this suffices):

$$\int _{a \in E} f(a) \left( \sum _{n=1}^\infty \mu _i\right) (da) = \sum _{n=1}^\infty \int _{a \in E} f(a) \mu _i(da)$$

$$\mu \le \nu \implies \int _{a \in E} f(a) \mu (da) \le \int _{a \in E} f(a) \nu (da)$$

$\int _{a \in E} f(a) \delta (x)(da) = f(x)$ is straightforward. For the other properties, see [31].

Theorem 1

(Fubini’s theorem). For s-finite measures $\mu :\varSigma _A \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _B \rightarrow [0,\infty ]$ and any measurable function $f :A \times B \rightarrow [0, \infty ]$,

$$ \int _{a \in A} \int _{b \in B} f(a,b) \mu '(db) \mu (da) = \int _{b \in B} \int _{a \in A} f(a,b) \mu (da) \mu '(db) $$

For s-finite measures $\mu :\varSigma _{\overline{A}} \rightarrow [0,\infty ]$ and $\mu ' :\varSigma _{\overline{B}} \rightarrow [0,\infty ]$ and any measurable function $f :A \times B \rightarrow [0, \infty ]$,

$$ \int _{a \in \overline{A}} \int _{b \in \overline{B}} \overline{f}(a,b) \mu '(db) \mu (da) = \int _{b \in \overline{B}} \int _{a \in \overline{A}} \overline{f}(a,b) \mu (da) \mu '(db) $$

Proof

Let $\mu = \sum _{i \in \mathbb {N}} \mu _i$ and $\mu ' = \sum _{i \in \mathbb {N}} \mu _i'$ for bounded measures $\mu _i$ and $\mu _i'$.

$$\begin{aligned}&\int _{a \in A} \int _{b \in B} f(a,b) \mu '(db) \mu (da) \\ =&\sum _{i,j \in \mathbb {N}} \int _{a \in A} \int _{b \in B} f(a,b) \mu _j'(db) \mu _i(da)&\text{ Lemma } \text{19 } \\ =&\sum _{i,j \in \mathbb {N}} \int _{b \in B} \int _{a \in A} f(a,b) \mu _i(da) \mu _j'(db)&\text{ Fubini } \text{ for } \sigma \text{-finite } \text{ measures } \, \mu _i, \mu _j' \\ =&\int _{b \in B} \int _{a \in A} f(a,b) \mu (da) \mu '(db) \end{aligned}$$

The proof in the presence of exception state is analogous.

Lemma 20

Fubini does not hold for the counting measure $c :\mathcal {B} \rightarrow [0,\infty ]$ and the Lebesgue measure $\lambda :\mathcal {B} \rightarrow [0,\infty ]$ (because c is not s-finite).

Proof

$$\begin{aligned} \int _{x \in [0,1]} \int _{y \in [0,1]} [x=y] c(dy) \lambda (dx)&= \int _{x \in [0,1]} 1 \lambda (dx) = 1 \\ \int _{y \in [0,1]} \int _{x \in [0,1]} [x=y] \lambda (dx) c(dy)&= \int _{y \in [0,1]} 0 c(dy) = 0 \end{aligned}$$

1.3 A.3 Kernels

Lemma 21

Let $\kappa _1,\kappa _1' :A \mapsto \overline{B}$ and $\kappa _2,\kappa _2' :B \mapsto \overline{C}$ be s-finite kernels.

If $\kappa _1 \le \kappa _1'$ holds pointwise, then

$$ \kappa _1>\!=\!>\kappa _2 \le \kappa _1'>\!=\!>\kappa _2 $$

If $\kappa _2 \le \kappa _2'$ holds pointwise, then

$$ \kappa _1>\!=\!>\kappa _2 \le \kappa _1>\!=\!>\kappa _2' $$

Proof

Assume $\kappa _2 \le \kappa _2'$. Thus, $\overline{\kappa _2} \le \overline{\kappa _2'}$. Now, let $a \in A$, $S \in \varSigma _{\overline{C}}$.

$$\begin{aligned} (\kappa _1>\!=\!>\kappa _2)(a)(S)&= \int _{b \in \overline{B}} \overline{\kappa _2}(b)(S) \, \kappa _1(a)(db) \\&\le \int _{b \in \overline{B}} \overline{\kappa _2'}(b)(S) \, \kappa _1(a)(db)&\overline{\kappa _2} \le \overline{\kappa _2'}, \text{ Lemma } \text{19 } \\&= (\kappa _1>\!=\!>\kappa _2')(a)(S) \end{aligned}$$

The proof for $\kappa _1>\!=\!>\kappa _2 \le \kappa _1'>\!=\!>\kappa _2$ works analogously.

Lemma 3

$(;\!)$ is associative, left- and right-distributive, has neutral element⁴ $\delta$ and preserves (sub-)probability and s-finite kernels.

Proof

Remember that $(f ;\!g)(a)(S) = \int _{b \in B} g(b)(S) \, f(a)(db)$. Left- and right-distributivity and the neutral element $\delta$ follow from properties of the Lebesgue integral in Lemma 19.

Associativity and preservation of (sub-)probability kernels is well known (see for example [12]). For s-finite kernels $f=\sum _{i \in \mathbb {N}} f_i$ and $g=\sum _{i \in \mathbb {N}} g_i$ and $h=\sum _{i \in \mathbb {N}} h_i$, we have (for sub-probability kernels $f_i$, $g_i$, $h_i$)

$$\begin{aligned}&(f ;\!g) ;\!h = \left( \left( \sum _{i \in \mathbb {N}} f_i \right) ;\!\left( \sum _{j \in \mathbb {N}} g_j \right) \right) ;\!\sum _{k \in \mathbb {N}} h_k = \sum _{i,j,k \in \mathbb {N}} (f_i ;\!g_j) ;\!h_k \\ =&\sum _{i,j,k \in \mathbb {N}} f_i ;\!(g_j ;\!h_k) = f ;\!(g ;\!h) \end{aligned}$$

$(;\!)$ preserves s-finite kernels because for s-finite kernels f and g, we have (for sub-probability kernels $f_i$, $g_i$) $f ;\!g = \sum _{i,j \in \mathbb {N}} f_i ;\!g_i$, a sum of kernels.

Lemma 4

For $f :A \mapsto \overline{B}$ and $g :B \mapsto \overline{C}$, $a \in A$ and $S \in \varSigma _{\overline{C}}$,

$$(f>\!=\!>g)(a)(S) = (f ;\!g)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S) f(a)(\{ x \})$$

Proof

$$\begin{aligned} (f>\!=\!>g)(a)(S)&= \int _{b \in \overline{B}} \overline{g}(b)(S) \, f(a)(db) \\&= \int _{b \in B} \overline{g}(b)(S) \, f(a)(db) + \int _{b \in \mathcal {X}} \overline{g}(b)(S) \, f(a)(db) \\&= \int _{b \in B} g(b)(S) \, f(a)(db) + \sum _{b \in \mathcal {X}} \overline{g}(b)(S) \, f(a)(\{x\}) \\&= (f ;\!g)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)f(a)(\{x\}) \end{aligned}$$

Lemma 5

$>\!=\!>$ is associative, left-distributive (but not right-distributive), has neutral element $\delta$ and preserves (sub-)probability and s-finite kernels.

Proof

Remember that $(f>\!=\!>g)(a)(S) = \int _{b \in \overline{B}} \overline{g}(b)(S) \, f(a)(db)$. Left-distributivity follows from the properties of the Lebesgue integral in Lemma 19. Right-distributivity does not necessarily hold because $\overline{g_1+g_2}(\bot ) \ne \overline{g_1}(\bot )+\overline{g_2}(\bot )$. Associativity for $f :A \mapsto \overline{B}$, $g :B \mapsto \overline{C}$ and $h :C \mapsto \overline{D}$ can be derived by

$$\begin{aligned}&((f>\!=\!>g)>\!=\!>h)(a)(S) \\ =\,&\Big ( \Big (f>\!=\!>g \Big ) ;\!h \Big )(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)(f>\!=\!>g)(a)(\{x\}) \\ =\,&\Big ( \Big (f ;\!g + \lambda a'. \lambda S'. \sum _{x \in \mathcal {X}} \delta (x)(S')f(a')(\{x\}) \Big ) ;\!h \Big )(a)(S) \\&+ \sum _{x \in \mathcal {X}} \delta (x)(S)(f>\!=\!>g)(a)(\{x\}) \\ =\,&(f ;\!g ;\!h)(a)(S) + \underbrace{\Big ( \Big ( \lambda a'. \lambda S'. \sum _{x \in \mathcal {X}} \delta (x)(S')f(a')(\{x\}) \Big ) ;\!h \Big )(a)(S)}_{=0 ((;\!) \text{ integrates } \text{ over } \text{ non-exception } \text{ states) }} \\&+ \sum _{x \in \mathcal {X}} \delta (x)(S)(f>\!=\!>g)(a)(\{x\}) \\ =\,&(f ;\!g ;\!h)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)\Big ((f ;\!g)(a)(\{x\}) + \sum _{x' \in \mathcal {X}} \delta (x')(\{x\})f(a)(\{x'\})\Big ) \\ =\,&(f ;\!g ;\!h)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)\Big ((f ;\!g)(a)(\{x\}) + f(a)(\{x\})\Big ) \\ =\,&(f ;\!g ;\!h)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)(f ;\!\lambda a'. \lambda S'. g(a')(S'))(a)(\{x\}) \\&+ \sum _{x \in \mathcal {X}} \delta (x)(S)f(a)(\{x\}) \\ =\,&(f ;\!g ;\!h)(a)(S) + \Big (f ;\!\Big (\lambda a'. \lambda S'. \sum _{x \in \mathcal {X}} \delta (x)(S')g(a')(\{x\})\Big )\Big )(a)(S) \\&+ \sum _{x \in \mathcal {X}} \delta (x)(S)f(a)(\{x\}) \\ =\,&\Big (f ;\!\Big (g ;\!h + \lambda a'. \lambda S'. \sum _{x \in \mathcal {X}} \delta (x)(S')g(a')(\{x\})\Big )\Big )(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)f(a)(\{x\}) \\ =\,&\Big (f ;\!\Big (g>\!=\!>h\Big )\Big )(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S)f(a)(\{x\}) \\ =\,&(f>\!=\!>(g>\!=\!>h))(a)(S) \end{aligned}$$

Here, we have used Lemma 4, left- and right-distributivity of $(;\!)$.

To show that $f>\!=\!>g$ preserves s-finite kernels, let $f :A \mapsto \overline{B}$ and $g :B \mapsto \overline{C}$ be s-finite kernels. Then, for sub-probability kernels $f_i$,

$$\begin{aligned} (f>\!=\!>g)(a)(S)&= (f ;\!g)(a)(S) + \sum _{x \in \mathcal {X}} \delta (x)(S) f(a)(\{ x \})\\&= (f ;\!g)(a)(S) + \sum _{x \in \mathcal {X}} \sum _{i \in \mathbb {N}} \delta (x)(S) f_i(a)(\{ x \}) \end{aligned}$$

Note that for each $x \in \mathcal {X}$ and $i \in \mathbb {N}$, $\lambda a. \lambda S. \delta (x)(S) f_i(a)(\{ x \})$ is a sub-probability kernel. Thus, $f>\!=\!>g$ is a sum of s-finite kernels and hence s-finite.

Proving that for sub-probability kernels f and g, $f>\!=\!>g$ is also a (sub-)probability kernel is trivial, since we only need to show that $(f>\!=\!>g)(a)(\overline{C})=1$ (or $\le 1$).

Lemma 22

Let $(A,\varSigma _A)$ and $(B,\varSigma _B)$ be measurable spaces. Let $f :A \times B \rightarrow [0,\infty ]$ be measurable and $\kappa :A \mapsto B$ be a sub-probability kernel. Then, $f' :A \rightarrow [0,\infty ]$ defined by

$$ f'(a) := \int _{b \in B} f(a,b) \kappa (a)(db) $$

is measurable.

Proof

See Theorem 20 of [30].

Lemma 23

$\times$ and $\overline{\times }$ preserve (sub-)probability kernels.

Proof

Let $\kappa :A \mapsto B$ and $\kappa ' :A \mapsto C$ be (sub-)probability kernels. The fact that $(\kappa \times \kappa ')(a)(\cdot )$ for all $a \in A$ is a (sub-)probability measure is inherited from Lemma 2. It remains to show that $(\kappa \times \kappa ')(\cdot )(S)$ is measurable for all $S \in \varSigma _{B \times C}$, with

$$ (\kappa \times \kappa ')(a)(S) = \int _{b \in B} \int _{c \in C} [(b,c) \in S] \kappa '(a)(dc) \kappa (a)(db) $$

By Lemma 22, $f' :A \times B \rightarrow [0,\infty ]$ defined by $f'(a,b) = \int _{c \in C} [(b,c) \in S] \kappa '(a)(dc)$ is measurable, using the measurable function $f :(A \times B) \times C \rightarrow [0,\infty ]$ defined by $f((a,b),c)=[(b,c) \in S]$. Again by Lemma 22, $\int _{b \in B} \int _{c \in C} [(b,c) \in S] \kappa '(a)(dc) \kappa (a)(db)$ is measurable.

Proving that for (sub-)probability kernels $\kappa :A \mapsto \overline{B}$ and $\kappa ' :A \mapsto \overline{C}$, $\kappa \overline{\times } \kappa '$ is a (sub-)probability kernel proceeds analogously.

Lemma 6

$\times$ and $\overline{\times }$ for kernels preserve (sub-)probability and s-finite kernels, are associative, left- and right-distributive.

Proof

Associativity, left- and right-distributivity are inherited from respective properties of the product of measures established by Lemma 2. Sub-probability kernels are preserved by Lemma 23.

S-finite kernels are preserved because $\kappa \times \kappa ' = (\sum _{i \in \mathbb {N}} \kappa _i) \times (\sum _{i \in \mathbb {N}} \kappa _i') = \sum _{i,j \in \mathbb {N}} \kappa _i \times \kappa _j'$ (analogously for $\overline{\times }$).

B Proofs for Semantics

Lemma 7

For $\varDelta$ as in the semantics of the while loop, and for each $\sigma$ and each S, the limit $\lim _{n \rightarrow \infty } \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S)$ exists.

Proof

In general, $0 \le \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S) \le 1$. First, we restrict the allowed arguments for $\lim _{n \rightarrow \infty } \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S)$ to only those S with $\circlearrowleft \in S$. We prove by induction that $\varDelta ^{n+1}(\pmb {\circlearrowleft }) \le \varDelta ^{n}(\pmb {\circlearrowleft })$, meaning $\forall \sigma :\forall S :\circlearrowleft \in S \implies \varDelta ^{n+1}(\pmb {\circlearrowleft })(\sigma )(S) \le \varDelta ^{n}(\pmb {\circlearrowleft })(\sigma )(S)$. Hence, $\varDelta ^{n}(\pmb {\circlearrowleft })$ is monotone decreasing in n and lower bounded by 0, which means that the limit must exist.

As a base case, we have $\varDelta ^1(\pmb {\circlearrowleft })(\sigma )(S) \le 1 = \delta _{\circlearrowleft }(S) = \varDelta ^0(\pmb {\circlearrowleft })(\sigma )(S)$, because $\circlearrowleft \in S$. We proceed by induction with

$$\begin{aligned} \varDelta ^{n+1}(\pmb {\circlearrowleft })(\sigma )(S)&= \left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ,b). {\left\{ \begin{array}{ll} [\![P ]\!](\sigma ) \gg \!=\varDelta ^n(\pmb {\circlearrowleft }) &{} b \ne 0 \\ \delta (\sigma ) &{} b = 0 \end{array}\right\} } \right) (\sigma )(S) \\&\le \left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ,b). {\left\{ \begin{array}{ll} [\![P ]\!](\sigma ) \gg \!=\varDelta ^{n-1}(\pmb {\circlearrowleft }) &{} b \ne 0 \\ \delta (\sigma ) &{} b = 0 \end{array}\right\} } \right) (\sigma )(S) \\&= \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S) \end{aligned}$$

In the second line, we have used the induction hypothesis. This application is valid because $\kappa _2 \le \kappa _2'$ implies $\kappa _1>\!=\!>\kappa _2 \le \kappa _1>\!=\!>\kappa _2'$ (Lemma 21).

We proceed analogously when we restrict the allowed arguments for the kernel $\lim _{n \rightarrow \infty } \varDelta ^n(\pmb {\circlearrowleft })(\sigma )(S)$ to only those S with $\circlearrowleft \notin S$, proving $\varDelta ^{n+1}(\pmb {\circlearrowleft }) \ge \varDelta ^{n}(\pmb {\circlearrowleft })$ for that case.

Lemma 8

In the absence of exception states, and using sub-probability kernels instead of distribution transformers, the definition of the semantics of the while loop from [23] is equivalent to ours.

Definition 6

In [23], Kozen shows a different way of defining the semantics of the while loop. In our notation, and in terms of probability kernels instead of distribution transformers, that definition becomes

$$ [\![{{\mathbf {\mathtt{{while }}}}}\, e \; \{P\}\, ]\!]= \sup _{n \in \mathbb {N}} \sum _{k=0}^{n} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^k>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]$$

Here, exponentiation is in terms of Kleisli composition, i.e. $\kappa ^0=\delta$ and $\kappa ^{n+1} = \kappa>\!=\!>\kappa ^n$. The sum and limit are meant pointwise. Furthermore, we define filter by the following expression (note that $[\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]$ and $[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]$ are only sub-probability kernels, not probability kernels).

$$\begin{aligned}{}[\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]&= \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ,b). {\left\{ \begin{array}{ll} \delta (\sigma ) &{} b \ne 0 \\ \mathbf {0} &{} b = 0 \end{array}\right\} } \\ [\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]&= \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ,b). {\left\{ \begin{array}{ll} \delta (\sigma ) &{} b = 0 \\ \mathbf {0} &{} b \ne 0 \end{array}\right\} } \end{aligned}$$

To justify Lemma 8, we prove the more formal Lemma 24. Note that in the presence of exceptions (e.g. P is just ${{\mathbf {\mathtt{{assert}}}}}\, (0)$), Definition 6 does not make sense, because if

Lemma 24

For all S with $S \cap \mathcal {X}= \emptyset$

$$ \left( \sum _{k=0}^{n} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^k>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) = \varDelta ^{n+1}(\pmb {\circlearrowleft })(\sigma )(S) $$

Proof

For $n=0$, we have

$$\begin{aligned}&\left( \sum _{k=0}^{0} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^k>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\left( \Big ( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^0>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\Big (\delta>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\Big )(\sigma )(S) \\ =\,&[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!](\sigma )(S) \\ =\,&\left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ',b). {\left\{ \begin{array}{ll} \delta (\sigma ') &{} b = 0 \\ \mathbf {0} &{} b \ne 0 \end{array}\right\} } \right) (\sigma )(S) \\ =\,&\left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ',b). {\left\{ \begin{array}{ll} \delta (\sigma ') &{} b = 0 \\ \pmb {\circlearrowleft }(\sigma ') &{} b \ne 0 \end{array}\right\} } \right) (\sigma )(S)&\circlearrowleft \notin S \\ =\,&\left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ',b). {\left\{ \begin{array}{ll} \delta (\sigma ') &{} b = 0 \\ ([\![P ]\!]>\!=\!>\pmb {\circlearrowleft })(\sigma ') &{} b \ne 0 \end{array}\right\} } \right) (\sigma )(S)&S \cap \mathcal {X}= \emptyset \\ =\,&\varDelta ^1(\pmb {\circlearrowleft }) \end{aligned}$$

For $n \ge 0$, we have

$$\begin{aligned}&\left( \sum _{k=0}^{n+1} \Big ( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^k>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\left( \left( \sum _{k=0}^{n} \Big ( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^{k+1} + ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>P)^{0} \right)>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\left( \left( \sum _{k=0}^{n} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^{k+1} + \delta \right)>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\left( \left( \sum _{k=0}^{n} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^{k+1} \right)>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \qquad \qquad \text {since } S \cap \mathcal {X}= \emptyset \\&+\left( \delta>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\ =\,&\left( \left( \sum _{k=0}^{n} \Big ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]\Big )^{k+1} \right)>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) + [\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!](\sigma )(S) \\ =\,&\left( \left( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]>\!=\!>\sum _{k=0}^{n} ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!])^{k} \right)>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) (\sigma )(S) \\&+[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!](\sigma )(S) \\ =\,&\left( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]>\!=\!>\left( \sum _{k=0}^{n} ([\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!])^{k}>\!=\!>[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!]\right) \right) (\sigma )(S) \\&+[\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!](\sigma )(S) \\ =\,&\left( [\![{{\mathbf {\mathtt{{filter}}}}}\, (e) ]\!]>\!=\!>[\![P ]\!]>\!=\!>\varDelta ^{n+1}(\pmb {\circlearrowleft }) \right) (\sigma )(S) + [\![{{\mathbf {\mathtt{{filter}}}}}\, (\lnot e) ]\!](\sigma )(S) \\ =\,&\left( \delta \overline{\times } [\![e ]\!]>\!=\!>\lambda (\sigma ',b). {\left\{ \begin{array}{ll} [\![P ]\!](\sigma ') \gg \!=\varDelta ^{n+1}(\pmb {\circlearrowleft }) &{} b \ne 0 \\ \delta (\sigma ') &{} b = 0 \end{array}\right\} } \right) (\sigma )(S) \\ =\,&\varDelta ^{n+2}(\pmb {\circlearrowleft })(\sigma )(S) \end{aligned}$$

In particular, have have used that left-distributivity does hold in this case since $S \cap \mathcal {X}= \emptyset$.

C Probability Kernel

In the following, we list lemmas that are crucial to prove Theorem 2 (restated for convenience).

Theorem 2

The semantics of each expression $[\![e ]\!]$ and statement $[\![P ]\!]$ is indeed a probability kernel.

Lemma 25

Any measurable function $f :A \rightarrow [0, \infty ]$ can be viewed as an s-finite kernel $f :A \mapsto \mathbb {1}$, defined by $f(x)(\emptyset ) = 0$ and $f(x)(\mathbb {1}) = f(x)$.

Proof

We prove that f is an s-finite kernel. Let $A_\infty := \{ x \in A \mid f(x) = \infty \}$. Since f is measurable, the set $A_\infty$ must be measurable. $f(x)(S) = \sum _{i \in \mathbb {N}} [x \in A_\infty ][() \in S] + \sum _{i \in \mathbb {N}} f(x) [i \le f(x) < i+1][() \in S]$, which is a sum of finite kernels because the sets $A_\infty$ and $\{x \mid i \le f(x) < i+1\}=f^{-1}([i,i+1))$ are measurable. Note that any sum of finite kernels can be rewritten as a sum of sub-probability kernels.

Lemma 26

Let $\kappa ' :X \mapsto Y$ and $\kappa '' :X \mapsto Y$ be kernels, and $f :X \rightarrow \mathbb {R}$ measurable. Then,

$$\begin{aligned} \kappa (x)(S) = {\left\{ \begin{array}{ll} \kappa '(x)(S) &{} \text {if } f(x) = 0 \\ \kappa ''(x)(S) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

is a kernel.

Proof

Let $f_{=0}(x) := [f(x) = 0]$, $f_{\ne 0}(x) := [f(x) \ne 0]$. Then, $\kappa = f_{=0} \times \kappa ' + f_{\ne 0} \times \kappa ''$. Viewing $f_{=0}$ and $f_{\ne 0}$ as kernels $X \mapsto \mathbb {1}$ immediately gives the desired result.

Lemma 27

Let $(A,\varSigma _A)$ and $(B,\varSigma _B)$ be measurable spaces. Let $\{ A_i \}_{i \in \mathcal {I}}$ be a partition of A into measurable sets, for a countable set of indices $\mathcal {I}$. Consider a function $f :A \rightarrow B$. If $f_{|A_i} :A_i \rightarrow B$ is measurable for each $i \in \mathcal {I}$, then f is measurable.

Lemma 28

Let $f :A \rightarrow B$ be measurable. Then $\kappa :A \mapsto B$ with $\kappa (a) = \delta (f(a))$ is a kernel.

The following lemma is important to show that the semantics of the while loop is a probability kernel.

Lemma 29

Suppose $\{ \kappa _n \}_{n \in \mathbb {N}}$ is a sequence of (sub-)probability kernels $A \mapsto B$. Then, if the limit $\kappa = \lim _{n \rightarrow \infty } \kappa _n$ exists, it is also a (sub-)probability kernel. Here, the limit is pointwise in the sense $\forall a\in A :\forall S \in \varSigma _B :\kappa (a,S) = \lim _{n \rightarrow \infty } \kappa _n(a)(S)$.

Proof

For every $a \in A$, $\kappa (a, \cdot )$ is a measure, because the pointwise limit of finite measures is a measure. For every $S \in \varSigma _B$, $\kappa (\cdot , S)$ is measurable, because the pointwise limit of measurable functions $f_n :A \rightarrow \mathbb {R}$ (with $\mathcal {B}$ as the $\sigma$-algebra on $\mathbb {R}$) is measurable.

D Proofs for Consequences

In this section, we provide some proofs of consequences of our semantics, explained in Sect. 5.

Lemma 9

For function $F()\{ {{\mathbf {\mathtt{{while }}}}}\, 1 \; \{{{\mathbf {\mathtt{{skip}}}}}\, \}\,; {{\mathbf {\mathtt{{return }}}}}\, \, 0 \}$,

$$ \frac{1}{0} + F() \not \simeq F() + \frac{1}{0} $$

Proof

If we evaluate $\frac{1}{0}$ first, we will only have weight on $\bot$.

If instead, we first evaluate F(), we only have weight on $\circlearrowleft$, by an analogous calculation.

Lemma 10

If $[\![e_1 ]\!](\sigma )(\mathcal {X})=[\![e_2 ]\!](\sigma )(\mathcal {X})=0$ for all $\sigma$, then $e_1 \oplus e_2 \simeq e_2 \oplus e_1$, for any commutative operator $\oplus$.

Proof

$$\begin{aligned}{}[\![e_1 \oplus e_2 ]\!](\sigma )(S)&= [\![e_1 ]\!]\overline{\times } [\![e_2 ]\!]>\!=\!>\lambda (x,y). \delta (x \oplus y) \\&= \int _{z \in \overline{\mathbb {R}\times \mathbb {R}}} \overline{\lambda (x,y).\delta (x \oplus y)}(z)(S) ([\![e_1 ]\!]\overline{\times } [\![e_2 ]\!])(\sigma )(dz) \\&= \int _{(x,y) \in \mathbb {R}\times \mathbb {R}} \delta (x \oplus y)(S) ([\![e_1 ]\!]\times [\![e_2 ]\!])(\sigma )(d(x,y)) \\&= \int _{(y,x) \in \mathbb {R}\times \mathbb {R}} \delta (y \oplus x)(S) ([\![e_2 ]\!]\times [\![e_1 ]\!])(\sigma )(d(y,x)) \\&= [\![e_2 \oplus e_1 ]\!](\sigma )(S) \end{aligned}$$

Here, we crucially rely on the absence of exceptions (for the third equality) and Fubini’s Theorem (for the fourth equality).

Lemma 11

$e_1 \oplus (e_2 \oplus e_3)\simeq (e_1 \oplus e_2) \oplus e_3$, for any associative operator $\oplus$.

Proof

The important steps of the proof are the following.

$$\begin{aligned}{}[\![e_1 \oplus (e_2 \oplus e_3) ]\!]&= [\![e_1 ]\!]\overline{\times } [\![e_2 \oplus e_3 ]\!]>\!=\!>\lambda (x,s). \delta (x \oplus s) \\&= [\![e_1 ]\!]\overline{\times } \Big ([\![e_2 ]\!]\overline{\times } [\![e_3 ]\!]>\!=\!>\lambda (y,z). \delta (y \oplus z) \Big )>\!=\!>\lambda (x,s). \delta (x \oplus s) \\&= [\![e_1 ]\!]\overline{\times } \Big ([\![e_2 ]\!]\overline{\times } [\![e_3 ]\!]\Big )>\!=\!>\lambda (x,(y,z)). \delta (x \oplus y \oplus z) \\&= \Big ( [\![e_1 ]\!]\overline{\times } [\![e_2 ]\!]\Big ) \overline{\times } [\![e_3 ]\!]>\!=\!>\lambda ((x,y),z). \delta (x \oplus y \oplus z) \\&= [\![(e_1 \oplus e_2) \oplus e_3 ]\!]\end{aligned}$$

Here, we make crucial use of associativity for the lifted product of measures in Lemma 6.