1 Pioneering Computer Methods

The volumetric determination of mineral composition from petrophysical logs originated in efforts to estimate reliable porosity estimates that were confounded by variations in rock mineralogy. When Archie (1950) introduced the term ‘petrophysics’ he framed it in terms of “the physics of particular rock types” and then elaborated on the petrophysics of reservoir rocks. The petrophysical properties that he considered were restricted entirely to those “related to the pore and fluid distribution”. The reason was obvious in that almost all boreholes were drilled for the location of either hydrocarbons or useable water in commercial quantities. The mineralogy of the pore framework complemented the fluid content of the pore network, but estimations would be focused on the evaluation of pore volume, permeability, and fluid content. In monominerallic rocks, pore volumes could be estimated very simply by interpolating between two endpoints of mineral and fluid. In multiminerallic rocks, porosity estimates became more difficult and significant errors were introduced if the mineral properties were radically different from one another.

Probably the earliest application of a mathematical solution to the resolution of porosity in a multiminerallic rock was directed to Permian carbonate reservoirs in West Texas. Petrophysicists were frustrated by complex mineralogy in their attempts to obtain reliable porosity estimates from logs as described by Savre (1963). Porosities had been commonly estimated from neutron logs, but values were excessively high in zones that contained gypsum, caused by the hydrogen within the water of crystallization. If the density log was used, then porosity estimation was compromised by the occurrence of either anhydrite or gypsum. Collectively, the mix of dolomite, anhydrite, gypsum, and porosity meant that pore volumes could not be resolved by graphical methods such as crossplots and nomograms that were the standard procedures of that time.

It was recognized that lithologies composed of several minerals would require several porosity logs to be run in combination in order to estimate volumetric porosity. In the most simple solution model, the proportions of multiple components together with porosity could be estimated from a set of simultaneous equations for the measured log responses. These equations can be written in matrix algebra form as:

$$ CV = L $$

where C is a matrix of the component petrophysical properties, V is a vector of the component unknown proportions, and L is a vector of the log responses of the evaluated zone. The equation set describes a linear model that links the log measurements with the component mineral properties. Although porosity represents the proportion of voids within the rock, the pore space is filled with fluid whose physical properties make it a “mineral” component. The set of equations is then solved as an “inverse problem”, in which rock composition is deduced from the logging measurements. As a closed system of dolomite, anhydrite, gypsum, and porosity, a deterministic solution is possible from three log inputs, which were chosen as neutron, density, and acoustic velocity log measurements. The solution for the unknown vector, V is:

$$ V = C^{ - 1} L $$

where C−1 is the inverse of the C matrix.

Savre (1963) described how this procedure was coded in a computer program, as a pioneer application of computers to petrophysics. An example of the graphical output drafted from one of the earliest computer runs is shown in Fig. 24.1 (Alger et al. 1963), where profiles of porosity, dolomite, anhydrite, and gypsum are shown from a Permian San Andres Formation section in West Texas. At the time that this early application was made, computing power was typically provided by a single mainframe computer in the company or university which had extended computing times and limited memory, while programming code was a specialized and time-consuming task. The same application is very easy to implement today as a spreadsheet procedure, using standard matrix functions and graphical outputs.

Fig. 24.1
figure 1

Graphical output profiles of porosity, dolomite, anhydrite, and gypsum from one of the earliest computer runs that processed neutron, sonic, and density logs of a Permian San Andres Formation section in West Texas (from Savre 1963)

Full size image

The inverse solution is a simple and powerful procedure for compositional analysis, but its simplicity carries certain assumptions that must be considered carefully. In particular, the basic model contains no intrinsic constraint to preclude negative estimates of compositional proportions. A unity equation dictates the closure of the system so that the proportions collectively sum to unity. However, individual proportions can have a negative value or one that exceeds unity. Rather than representing mathematical error, apparently anomalous zones are located outside the composition space defined by the mineral endmembers as vertices. Consequently, the generation of negative proportions is a perfectly natural consequence of the model and can contain useful feedback information. If the negative values are small, then this is usually called by the stochastic nature of the input nuclear logs coupled with borehole rugosity perturbations. If large, the possibility of washouts and gas effects should be examined before evaluating the possibility of another mineral that is not included in the composition model.

If these explanations are not sufficient, then negative proportions of components have a role as a basic check on the validity of the model used for compositional analysis. As such, they are diagnostic errors with an information content to be used to guide the analysis to a better solution. The distinction between errors that are acceptable as minor, random measurement noise and systematic deviations is best made by a comparison between the original logs and the logs predicted by the model solution. The predictions are given by:

$$ \hat{L} = CV $$

If the inverse procedure has generated zone solutions with proportions that are negative or exceed unity, then the adjustment to rational proportions will result in log predictions that will deviate from the original logs. The deviations between measurements and predictions can then be examined to differentiate minor measurement error from systematic perturbations that require intervention and correction. In the more sophisticated models to be reviewed, tool response errors are actively incorporated within the solution algorithm, together with constraints that preclude irrational compositional proportions.

However, if the solution results in compositional proportions that are all positive, then there will be an exact match between the logs and model predictions. This equivalence does not imply that the result is geologically correct; it simply means that the solution is rational and consistent with the choice of components and their properties. There may be other satisfactory solutions based on alternative mineral suites.

2 Mineralogy of Underdetermined Systems

The basic compositional inversion procedure requires a precise match between the number of knowns and unknowns. This situation is a “determined system”. The alternative possibilities are that the number of logs is insufficient to provide a unique resolution of the proportions of the components (an underdetermined system) or that the number of logs exceeds the number of components (an overdetermined system). In reality, it is likely that most formations present underdetermined compositional problems, if all the constituents are counted and matched against the number of logs run in a typical borehole. As counterpoint, many of the minerals will be found in small quantities and the overall composition dominated by a few components.

McCammon (1970) and Harris and McCammon (1971) considered alternative model procedures to the estimation of mineral compositions from logs in underdetermined cases. Although their algorithms have been superseded by optimization procedures, their approach is instructive concerning the role of information in log compositional analysis and the potentially competing criteria of mathematical optimality and geological reality. McCammon (1970) considered the underdetermined system. In terms of classical information theory, which proposes that the least biased solution is the one that maximizes the entropy function:

$$ E = \sum {p_{i} } \log p_{i} $$

where pi is the proportion of the ith component. This equation for entropy is closely approximated by that for proportional variance:

$$ \begin{aligned} P & = \left( {\frac{n}{n - 1}} \right)\sum {v_{i} (1 - v_{i} )} \\ & = \left( {\frac{n}{n - 1}} \right)\left( {1 - \sum {v_{i}^{2} } } \right) \\ \end{aligned} $$

The maximum of the variance function, P, is close to the condition of maximum entropy, and the resulting optimal solution is easier to compute using the matrix algebra equation:

$$ V = C^{t} (CC^{t} )^{ - 1} L $$

where V is the vector of unknown proportions, C is the matrix of component log properties, t signifies a matrix transpose, and L is the vector of zone log responses (Doveton and Cable 1979).

The compositional solution from the proportional variance algorithm is optimal from a classical statistical viewpoint: the average squared errors between estimates and real compositions should be the minimum possible.

This is a conservative philosophy that aims to be least wrong or risk-averse with a minimum error as penalty. However, mineral proportions are frequently distributed in a highly unequal manner. Therefore the real rock composition will often be one of several extreme possibilities, rather than the less likely seemingly homogeneous composition that can result from a minimum variance solution. The correct interpretation of a bland compositional solution is that it represents the average of a range of possibilities. As such, it is a good estimate of the average, but may be a very poor prediction of the particular: the composition of the zone in question. Such a result is a useful diagnostic that suggests that several extreme alternatives should be reviewed and that extra information is required. The information can take a variety of forms, such as explicit geological knowledge of the range of actual compositions, or the use of additional constraints that preclude impossible solutions.

3 Mineralogy of Overdetermined Systems

Many rocks are dominated by a relatively small number of components, so that the number of logging tool measurements may exceed the number of significant lithological components. The situation becomes overdetermined when the number of log response equations is greater than the number of components. The appropriate solution is then one that most accurately reproduces the original logs when logs are calculated as predictions from the compositional solutions. Using conventional statistical theory, this solution is the one that minimizes the sums of squares of the deviations between the original logs and their predictions. The least-squares solution is given readily by the matrix algebra equation:

$$ V = (C^{t} C)^{ - 1} C^{t} L $$

where the terms are the same as those in both the determined and underdetermined matrix algorithms written earlier. The matrix formulation requires some additional weighting function to allow for the fact that the logging measurements are recorded in radically different units. Without any weighting, the error minimization is predicated on equal units and results in a solution which preferentially honors logs with the highest data ranges. The modified least-squares algorithm is then:

$$ V = (C^{t} WC)^{ - 1} C^{t} WL $$

where W is a diagonal matrix that contains the elements of a weight vector (Harvey et al. 1990). The weights may be assigned based on physical first principles or by a standardization scheme, such as transformation from the original measurement to a scale anchored to the mean and counted in standard deviation units.

For any given zone, the sum of squares error is given by:

$$ e = \left( {L - \hat{L}} \right)^{t} \left( {(L - \hat{L})} \right) $$

where \( \hat{L} \) is the vector of log responses associated with the least-squares solution. The error term can be plotted as a monitor log to highlight zones where there are striking inconsistencies between the model and the log responses. The overall performance of an algorithm may be judged from the standard error, computed from the summed zone errors as:

$$ s_{e} = \sqrt {\frac{\varSigma e}{(n - m - 1)}} $$

where n is the number of observations and m is the number of logs.

4 Optimization Methods

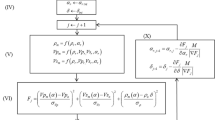
Current compositional analysis procedures has moved beyond simple inversion algorithms described, so that constraints and tool error functions have been incorporated as part of the solution process. The methodology was first developed by Mayer and Sibbit (1980) who applied modified steepest-descent strategies to hunt for an optimal solution that minimized the “incoherence” between the logs and their predicted values. For any given log, the incoherence function is given by:

$$ I_{A} = \frac{{(a - \hat{a})^{2} }}{{\left( {\sigma_{A}^{2} + \tau_{A}^{2} } \right)}} $$

where I A is the incoherence for log A, a is the log response for the zone and \( \hat{a} \) is its prediction, \( \sigma_{A}^{2} \) and \( \tau_{A}^{2} \) are the uncertainties associated with the log measurement and the response equation, respectively.

The uncertainty term for each log measurement is compounded from the sources of sensor error, data acquisition, and the dispersions associated with environmental corrections. Response equation dispersion represents the uncertainties introduced by linear approximations, erroneous choices of component log responses, and hidden factors such as the influence of textural parameters. It seems reasonable to suppose that these two types of uncertainty are independent, so that they can be summed as one total error term for each tool:

$$ u_{A}^{2} = \sigma_{A}^{2} + \tau_{A}^{2} $$

The total log incoherence for any particular depth zone is the sum of the separate log incoherences:

$$ I_{t} = I_{A} + I_{B} + I_{C} + \cdots $$

The form of the equations shows that the solution will tend to be most strongly influenced by the logs to which the most confidence can be attributed. Logs with large errors will have greater incoherences and will contribute more to the total incoherence term.

Constraints are also included and take the general form of:

$$ g_{i} (v_{i} ) \ge 0 $$

where gi is some function that constrains the value of the unknown proportion of the ith component. Rigid, mathematical constraints are those that preclude the occurrence of proportions that are negative or those that exceed unity. Geological and local constraints incorporate relations that conform to general geological principles or prior knowledge of local geology. These geological constraints are more generalized, so that appropriate uncertainties are assigned to them. The constraint dispersions generate additional incoherence terms to be considered. A combined incoherence function is then the sum of the log and constraint incoherences:

$$ I_{t} = \sum {\frac{{(a_{i} - \hat{a}_{i} )^{2} }}{{\sigma_{i}^{2} + \tau_{i}^{2} }}} + \sum {\frac{{g_{i} (v_{j} )^{2} }}{{\tau_{j}^{2} }}} $$

Notice that if the system is fully determined, then the total incoherence will be zero, provided that no constraints are violated. This special situation is the limiting case of applications which are otherwise presumed to be overdetermined. In a routine application of the optimization algorithm, the number of logs would be expected to exceed the number of components. In part, this is feasible because the bulk of rock compositions tend to be dominated by relatively few components. In addition, the range of wireline measurements used today typically extends beyond the traditional porosity logs to resistivity, spectral gamma ray and geochemical logs.

The optimization method of Mayer and Sibbit (1980) is an iterative search procedure. The system model of input logs and output components are first defined. The incoherence values associated with each log type are entered, together with the constraints to be met. For each zone, an initial composition is estimated by an approximate method and used as the starting point for a sequence of intermediate solutions. At each step, the incoherence is calculated between the input log responses and those predicted from the solution. A gradient is also computed as the means to generate the next solution, using a steepest descent technique. The process terminates when it is determined that convergence has been satisfied, at which time there is no appreciable difference between successive solutions. The final solution will be approximate, but the total incoherence between the logs and the compositional estimate will be the minimum possible. The combined display of real and theoretical logs is invaluable as a quality control mechanism to alert the user to problem zones which may be optimal, but are flatly wrong. The generality of the approach allows alternative and remedial attempts to be made without major difficulty.

In further refinements, Gysen et al. (1987) described an extension of the method to the simultaneous optimization of component proportions and response parameters. Moss and Harrison (1985) also reported a technique to solve for the uncertainty multipliers which contain the total error associated with each tool. Although the errors cannot be solved for every depth zone, they can at least be estimated for selected intervals and assumed to be effectively constant between zones.

Phyllosilicate minerals pose a difficult problem because their composition is so variable. However, the clay mineral properties listed provide a useful reference standard in the estimation of hypothetical composition volumes in the absence of explicit information keyed to the formation that is analyzed. The estimates can be considered as normative, as contrasted with modal predictions of clay mineral proportions based on X-ray diffraction analyses from core.

Optimal, minimum error solutions are worthless if the component model is incorrectly specified. Meaningful results are best obtained by patient geological evaluation of a sequence of solutions where the results of each are used to an improvement of the successive solution. Modern compositional analysis software utilizes the power of the error minimization method, but allows user interaction so that alternative geological models can be compared.

Quirein et al. (1986) described the use of quadratic programming techniques and linearized response equations, as an improvement on the penalty constraint approach used by earlier methods. In addition, they incorporated a program to solve for poorly known log responses of a component subset, as an optimization procedure applied to specific depths that could be used for calibration. These calibration intervals are those where both logs and compositions are known and are most typically those that have been cored. In addition, knowledge of composition could be utilized from other sources. Not all component log responses need to be estimated since their properties are restricted to a limited range. However, a subset of mineral components have ambiguous and locally variable properties. The most notorious example of such components are clay minerals, and these will be discussed more fully in the following section.

In common with earlier optimization methodologies, the system is assumed to be either determined or overdetermined. The use of multiple alternative models then allows a more realistic treatment of this assumption, in which common associations can be modeled in parallel and a final selection made between them at any depth. Wherever possible, each separate model is designed to be close to fully determined in an attempt to find a good match and to sidestep problems associated with the estimates of log and equation dispersions (Marett and Kimminau 1990). The appropriate logs for each model are clearly those that discriminate well between the separate components. If a poor choice of logs is made, then the model is ill-conditioned. The model structure can be checked through the computation of the condition number of:

$$ C^{t} DC $$

where C is the matrix of component log responses and D is a matrix of uncertainty values. The condition number is higher for ill-conditioned models and gives a measure of the sensitivity of proportion estimates to small changes in component log responses (Quirein et al. 1986). The choice between alternative models for any zone can be made by the user based on an assessment of the relative incoherence of the solutions and their feasibility as reasonable geological descriptions. Alternatively, the decision can be made on the basis of probability established either from comparison of alternative solutions or the use of a Bayesian prior probability.

While generally still applied to an overdetermined system, the multiple models are not far removed from determined matches of components and logs. Where a model becomes determined, the solution is that of a simple and fast matrix inversion with zero incoherence, provided that the non-negative constraint is not violated. The analysis of the relative conditioning of the model system is a valuable mathematical contribution to the determination of which logs provide the maximum discrimination of model components that will lead to the most stable estimates of volumetric proportions.

5 Clay Component Estimation

Shales are composed typically of a mixture of clay minerals, quartz, carbonates, and iron minerals, as well as other accessory components. Clay minerals are markedly different from other rock-forming minerals in terms both of their complexity and variability. Shales present special problems for log interpretation and while many algorithms have been designed for their volumetric estimation, the meaning and limitations of their results should be understood.

In more detailed work, the older and broader methods of shale evaluation have been expanded to the quantitative assessment of clay mineral species. Clay minerals show differing degrees of variability, but are generally subdivided between four major types: illite, smectite, kaolinite, and chlorite. Clay mineral typing is based on several log criteria which must be considered carefully and collectively. Ellis (1987, pp. 460–461) noted that the four principal clay mineral types could be combined into two types, based on their hydroxyl content. Kaolinite and chlorite have eight hydroxyls, as contrasted with four for smectite and illite. The neutron log is sensitive to this difference, which can be used as one diagnostic guide, through comparison of the neutron and density porosities when they are both scaled with respect to a quartz matrix. The photoelectric factor is also a useful clay discriminator because of its control by the aggregate atomic number. Ellis (1987, pp. 451–454) pointed out that iron-free aluminosilicate clays would have photoelectric absorption characteristics that are virtually the same as for quartz. Therefore, variations in the photoelectric factor within shales are primarily a reflection of iron content. Overall, there is a tendency for a progressive increase in iron from low values in kaolinite, through smectite and illite, to high values for iron-bearing chlorite. Distinctions between clay minerals can also be made on the basis of spectral gamma-ray logs, particularly in the differentiation of relatively potassium–rich illites from low-potassium kaolinite and chlorite.

The quantitative estimation of clay mineral abundances from the neutron, density, photoelectric factor, and spectral gamma ray measurements is fraught with difficulties. Wide compositional changes within clay mineral groups pose special problems. Useful quantitative models are not easy to define and are frequently ambiguous in their interpretation. The most realistic approach would be to coordinate log measurements with laboratory analyses of core samples. The core values may be idealized as a calibration standard in the development of a statistical prediction model for clay minerals from logs. Even this strategy must be considered thoughtfully and honestly. The most widely used laboratory method to estimate quantities of clay minerals is that of X-ray diffraction. Even with careful sample preparation procedures, the error of clay mineral estimates from X-ray diffraction can be routinely expected to be 50% or more of the reported value (Eslinger and Pevear 1988, p. A-24). Nevertheless, an important result is that at least the appropriate mineral subset can be identified with some confidence. This ensures that the correct components will be selected for compositional analysis from logs. Reconciliation of the log estimates with X-ray diffraction analyses should then be made within a model that attributes appropriate error magnitudes to both data sources.

6 Normative Estimation by Geochemical Logs

Geochemical logging tools measure induced gamma-ray spectra that are created when a formation is bombarded by high energy neutrons from an electronic pulsed source. A matrix inversion spectral fit algorithm then separates the spectrum into individual elemental sources. The major rock composition elements of silicon, calcium, magnesium, iron, sulfur, titanium and carbon are estimated together with the rare earth, gadolinium. In addition, potassium, thorium, uranium can be estimated from the natural gamma rays emitted by formations and measured by the spectral gamma-ray log. As a consequence of the direct relationship between elemental data and mineral compositions more realistic mineral transforms have been developed that are a major improvement on models based on mineral properties. However, a distinction must be made between normative minerals that are computed from transforms of elemental data and modal minerals that are observed visually or by petrographic laboratory methods such as X-ray diffraction or infra-red spectroscopy. Clearly, the fundamental goal of an effective transform is to provide a close match between normative mineral solutions and modal mineral suites.

“Normative” minerals calculated from oxide analyses have been a standard procedure in igneous petrology since the CIPW (Cross-Iddings-Pirsson-Washington) norm was introduced by Cross et al. (1902). These normative minerals are contrasted with modal compositions that are commonly measured by point-counting of minerals in thin-sections of rock. The normative concept has also been extended to sedimentary rocks in attempts to compute realistic mineral assemblages. Krumbein and Pettijohn (1938) pp. 490–492 explained the molecular ratio method to calculate the probable mineral composition of a rock, based on chemical analyses of oxide percentages. As a first step, the minerals to be resolved are first identified from thin-section observation or other sources of information. The molecular ratios are then assigned in a stepwise fashion to the minerals. The process consists of a logical order of steps that first accommodates unique associations between oxides and certain minerals, and then allocates the remainder to other components. Imbrie and Poldervaart (1959) described a commonly used method of sedimentary normative analysis and then compared the results with modal estimates of mineralogy. From a detailed study of the Permian Florena Shale, they concluded that estimates of the chert, calcite, dolomite, and clay had errors of less than 5%. However, there was little agreement between computed clay mineral proportions and those produced from X-ray diffraction analysis. Imbrie and Poldervaart (1959) were not surprised by this discrepancy, but attributed it to the known high variability of clay mineral compositions through isomorphous substitution.

Essentially the same problems are tackled in the computation of sedimentary normative minerals, when based on elements measured by geochemical logs (Herron 1986). However, many of the older normative methods predated computers. The classical norm calculation is subtractive, deterministic and rigidly leveraged. As discussed by Harvey et al. (1990), the method can be useful when certain elements can be assigned totally to single individual minerals. These assignations can then be made in an ordered protocol of analysis partition between mineral species. Otherwise, the use of simultaneous equations to link mineral compositions with elemental measures is a much more general and powerful method. The speed of modern software also allows real-time interaction between petrophysicist and machine, so that alternative models can be evaluated quickly and decisions made that blend mathematical optimality with geological credibility. Any analysis should be preceded by some notion of what constitutes a fit-for-purpose estimation. Less accuracy is needed if the intent is for a generalized semi-quantitative description of variation rather than more rigorous estimates for use in quantitative basin modeling or physical property predictions (Harvey et al. 1998).

The model that links minerals with elements can be set up as a fully determined system and solved by standard matrix inversion using methods described earlier. Whenever the components are computed as positive proportions, then the compositional solution is rational and honors the analysis perfectly. However, in common with the normative model, any apparent precision read into the result is illusory because the determined system makes no allowance for analytical error. It is usually practical to model a rock with a set of minerals that are fewer in number than the elements available from geochemical logging. The system is then overdetermined and can be resolved by one or other of a variety of optimization techniques. The additional complexity in computation is offset by several distinct advantages. The overdetermination allows constraints and error functions to be incorporated, both for optimal solution control and diagnostic evaluation of sources of analytical error. The choice of an overdetermined system also provides better assurance of a stable solution in situations where the mineral response matrix becomes sparse or there are potential compositional colinearities that link some of the mineral subsets (Harvey et al. 1990).

Strictly speaking, there will almost always be more minerals than elements to solve for them, so that the problem is always underdetermined. However, as Herron (1988) noted, the overwhelming majority of sedimentary rocks are composed of only ten minerals: quartz, four clays, three feldspars, and two carbonates. In practice, reasonable compositional solutions can be generated using relatively small mineral sub-sets, provided that they have been identified correctly and that the compositions used are both fairly accurate and constant. Alternatively, the inversion procedure can be run as an unconstrained procedure and components with negative proportions eliminated from the model. Harvey et al. (1998) found this approach to be successful, but cautioned that negative components should be eliminated one at a time, starting with the largest negative component, because of interactions between the components.

Mineral solutions may be calculated by two alternative strategies. In the first, the average chemical compositions of minerals drawn from a large data-base are used as endmember responses and resolved by standard matrix inversion procedures. This result is normative and generic in the sense that it is based on a sample drawn from a universal mineral reference set and applied to a specific sequence where local mineral compositions may deviate from the global average. The result is hypothetical, but has the particular advantage that comparisons can be made between a variety of locations and do not require expensive ancillary core measurements. New methods of classification may also be necessary as discussed by Herron (1988) in his study of terrigenous sands and shales in terms both of core and geochemical log data.

In a second approach, the solution is calibrated to core data, where laboratory determinations of mineralogy and elemental geochemistry are analyzed by multiple regression techniques to determine local mineral compositions. This result is linked to petrography and so is philosophically closer to an estimated modal solution, rather than the more hypothetical normative model. As mentioned earlier, realistic statistical calibration models should incorporate error terms from all sources of measurement. When geochemical logging was first introduced, several detailed studies were made to assess the strengths and limitations of borehole geochemistry through exhaustive comparisons with core elemental and mineralogical analyses. These included comparisons in the Conoco Research well, Ponca City, Oklahoma by Hertzog et al. (1987); the discussion of the results from an Exxon research well which penetrated Upper Cretaceous siliciclastic rocks in Utah by Wendlandt and Bhuyan (1990); and an assessment of data from three Shell wells in the Netherlands, Oman, and the U.S. by van den Oord (1990).

There are several ways to assess modal mineralogy, so which constitutes the most accurate method to use as a standard for the real mineral composition? Harvey et al. (1998) addressed this problem when they compared core data from the spectral measurements of quantitative X-ray diffraction and infrared spectroscopy, as well as micrometric analysis from thin section point counts. Overlapping peaks and poor resolution at low resolution pose special problems for the spectral methods, while appropriate sample sizes must be observed for robust statistics in micrometric analysis. Also, the distinction between volume percentage and weight percentage must be observed when interrelating modal and normative compositions. Harvey et al. (1998) concluded that the results of their study did not favor one method over another, but pointed out that their comprehensive analysis demonstrated the difficulty of obtaining accurate modal estimates and even the notion of what constitutes the “real” mineral composition. This is certainly worth bearing in mind when making a judgement about the “accuracy” of a normative mineral solution from inversion of log responses. So, for example, mismatches in clay mineral estimates by log inversion represents a failure to reproduce the results of quantitative X-ray diffraction which are themselves only estimates of the true composition.

A major obstacle to the production of unique mineral transformations from element concentrations has been the problem of compositional colinearity. If precisely colinear, then an infinite range of solutions is possible, causing a matrix singularity and a breakdown of an inversion procedure. If average mineral compositions are used, a solution becomes possible, but may be unstable (Harvey et al. 1998). Wendlandt and Bhuyan (1990) found that the use of silicon, potassium and aluminum tended to result in overestimates of kaolinite; the use of iron to predict illite content caused underestimates of kaolinite. However, effective discrimination between illite and kaolinite contents became possible when dry density was applied as an extra constraint.

7 Conclusion

The estimation of mineral composition from petrophysical logs is now a standard feature on any log analysis software package. However, the degree to which these estimates match reality is highly variable and requires a knowledgeable and experienced user to work with powerful procedures. The identification of the major mineral suite that actually occurs in the rock is an important first step. As the old Chinese proverb says, “The beginning of wisdom is calling a thing by its right name.” In the end, the solution of “mathematical minerals” will often come down to a choice between an acceptable estimate of an unreachable modal mineralogy or the realization of a useful, but hypothetical, normative assemblage.