Abstract
The Fujisaki-Okamoto (FO) transformation (CRYPTO 1999 and Journal of Cryptology 2013) turns any weakly secure public-key encryption scheme into a strongly (i.e., \(\mathsf {IND}\text {-}\mathsf {CCA}\)) secure one in the random oracle model. Unfortunately, the FO analysis suffers from several drawbacks, such as a non-tight security reduction, and the need for a perfectly correct scheme. While several alternatives to the FO transformation have been proposed, they have stronger requirements, or do not obtain all desired properties.
In this work, we provide a fine-grained and modular toolkit of transformations for turning weakly secure into strongly secure public-key encryption schemes. All of our transformations are robust against schemes with correctness errors, and their combination leads to several tradeoffs among tightness of the reduction, efficiency, and the required security level of the used encryption scheme. For instance, one variant of the FO transformation constructs an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure scheme from an \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure one with a tight reduction and very small efficiency overhead. Another variant assumes only an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure scheme, but leads to an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure scheme with larger ciphertexts.
We note that we also analyze our transformations in the quantum random oracle model, which yields security guarantees in a post-quantum setting.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The notion of INDistinguishability against Chosen-Ciphertext Attacks (\(\mathsf {IND}\text {-}\mathsf {CCA}\)) [34] is now widely accepted as the standard security notion for asymmetric encryption schemes. Intuitively, \(\mathsf {IND}\text {-}\mathsf {CCA}\) security requires that no efficient adversary can recognize which of two messages is encrypted in a given ciphertext, even if the two candidate messages are chosen by the adversary himself. In contrast to the similar but weaker notion of INDistinguishability against Chosen-Plaintext Attacks (\(\mathsf {IND}\text {-}\mathsf {CPA}\)), an \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary is given access to a decryption oracle throughout the attack.
Generic Transformations achieving \(\mathsf {IND}\text {-}\mathsf {CCA}\) Security. While \(\mathsf {IND}\text {-}\mathsf {CCA}\) security is in many applications the desired notion of security, it is usually much more difficult to prove than \(\mathsf {IND}\text {-}\mathsf {CPA}\) security. Thus, several transformations have been suggested that turn a public-key encryption (PKE) scheme with weaker security properties into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) one generically. For instance, in a seminal paper, Fujisaki and Okamoto [23, 24] proposed a generic transformation (FO transformation) combining any One-Way (\(\mathsf {OW}\text {-}\mathsf {CPA}\)) secure asymmetric encryption scheme with any one-time secure symmetric encryption scheme into a Hybrid encryption scheme that is \((\mathsf {IND}\text {-}\mathsf {CCA})\) secure in the random oracle model [7]. Subsequently, Okamoto and Pointcheval [32] and Coron et al. [18] proposed two more generic transformations (called REACT and GEM) that are considerably simpler but require the underlying asymmetric scheme to be One-Way against Plaintext Checking Attacks (\(\mathsf {OW}\text {-}\mathsf {PCA}\)). \(\mathsf {OW}\text {-}\mathsf {PCA}\) security is a non-standard security notion that provides the adversary with a plaintext checking oracle \(\textsc {Pco}(c,m)\) that returns 1 iff decryption of ciphertext c yields message m. A similar transformation was also implicitly used in the “Hashed ElGamal” encryption scheme by Abdalla et al. [1].
KEMs. In his “A Designer’s Guide to KEMs” paper, Dent [20] provides “more modern” versions of the FO [20, Table 5] and the REACT/GEM [20, Table 2] transformations that result in \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key-encapsulation mechanisms (KEMs). Recall that any \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure KEM can be combined with any (one-time) chosen-ciphertext secure symmetric encryption scheme to obtain a \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure PKE scheme [19]. Due to their efficiency and versatility, in practice one often works with such hybrid encryption schemes derived from a KEM. For that reason the primary goal of our paper will be constructing \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure KEMs.
We remark that all previous variants of the FO transformation require the underlying PKE scheme to be \(\gamma \)-spread [23], which essentially means that ciphertexts (generated by the probabilistic encryption algorithm) have sufficiently large entropy.
Security against Quantum Adversaries. Recently, the above mentioned generic transformations have gathered renewed interest in the quest of finding an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure asymmetric encryption scheme that is secure against quantum adversaries, i.e., adversaries equipped with a quantum computer. In particular, the NIST announced a competition with the goal to standardize new asymmetric encryption systems [31] with security against quantum adversaries. Natural candidates base their \(\mathsf {IND}\text {-}\mathsf {CPA}\) security on the hardness of certain problems over lattices and codes, which are generally believed to resists quantum adversaries. Furthermore, quantum computers may execute all “offline primitives” such as hash functions on arbitrary superpositions, which motivated the introduction of the quantum (accessible) random oracle model [11]. Targhi and Unruh recently proved a variant of the FO transformation secure in the quantum random oracle model [38]. Helping to find \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure KEM with provable (post-quantum) security will thus be an important goal in this paper.
Discussion. Despite their versatility, the above FO and REACT/GEM transformations have a couple of small but important disadvantages.
-
Tightness. The security reduction of the FO transformation [23, 24] in the random oracle model is not tight, i.e., it loses a factor of \(q_\mathsf {G}\), the number of random oracle queries. A non-tight security proof requires to adapt the system parameters accordingly, which results in considerably less efficient schemes. The REACT/GEM transformations have a tight security reduction, but they require the underlying encryption scheme to be \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure. As observed by Peikert [33], due to their decision/search equivalence, many natural lattice-based encryption scheme are not \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure and it is not clear how to modify them to be so. In fact, the main technical difficulty is to build an \(\mathsf {IND}\text {-}\mathsf {CPA}\) or \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure encryption scheme from an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure one, with a tight security reduction.
-
Correctness error. The FO, as well as the REACT/GEM transformation require the underlying asymmetric encryption scheme to be perfectly correct, i.e., not having a decryption error. In general, one cannot exclude the fact that even a (negligibly) small decryption error could be exploited by a concrete \(\mathsf {IND}\text {-}\mathsf {CCA}\) attack against FO-like transformed schemes. Dealing with imperfectly correct schemes is of great importance since many (but not all) practical lattice-based encryption schemes have a small correctness error, see, e.g., DXL [21], Peikert [33], BCNS [14], New Hope [3], Frodo [13], Lizard [17], and Kyber [12].Footnote 1
These deficiencies were of little or no concern when the FO and REACT/GEM transformations were originally devised. Due to the emergence of large-scale scenarios (which benefit heavily from tight security reductions) and the increased popularity of lattice-based schemes with correctness defects, however, we view these deficiencies as acute problems.
1.1 Our Contributions
Our main contribution is a modular treatment of FO-like transformations. That is, we provide fine-grained transformations that can be used to turn an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure PKE scheme into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure one in several steps. For instance, we provide separate \(\mathsf {OW}\text {-}\mathsf {CPA}\rightarrow \mathsf {OW}\text {-}\mathsf {PCA}\) and \(\mathsf {OW}\text {-}\mathsf {PCA}\rightarrow \mathsf {IND}\text {-}\mathsf {CCA}\) transformations that, taken together, yield the original FO transformation. However, we also provide variants of these individual transformations that achieve different security goals and tightness properties. All of our individual transformations are robust against PKE schemes with correctness errors (in the sense that the correctness error of the resulting schemes can be bounded by the correctness error of the original scheme).
The benefit of our modular treatment is not only a conceptual simplification, but also a larger variety of possible combined transformations (with different requirements and properties). For instance, combining two results about our transformations \(\mathsf {T}\) and \({\mathsf {U}}^{{\not \bot }}\), we can show that the original FO transformation yields \(\mathsf {IND}\text {-}\mathsf {CCA}\) security from \(\mathsf {IND}\text {-}\mathsf {CPA}\) security with a tight security reduction. Combining \({\mathsf {S}}^{\ell }\) with \(\mathsf {T}\) and \({\mathsf {U}}^{{\not \bot }}\), on the other hand, yields tight \(\mathsf {IND}\text {-}\mathsf {CCA}\) security from the weaker notion of \(\mathsf {OW}\text {-}\mathsf {CPA}\) security, at the expense of a larger ciphertext. (See Fig. 1 for an overview.)
Our Transformations in Detail. In the following, we give a more detailed overview over our transformations. We remark that all our transformations require a PKE scheme (and not a KEM). We view it as an interesting open problem to construct similar transformations that only assume (and yield) KEMs, since such transformations have the potential of additional efficiency gains.
Our modular transformations. Top: solid arrows indicate tight reductions, dashed arrows indicate non-tight reductions. Bottom: properties of the transformations. The tightness row only refers to tightness in the standard random oracle model; all our reductions in the quantum random oracle model are non-tight.
\(\mathsf {T}\): from \(\mathsf {OW}\text {-}\mathsf {CPA}\) to \(\mathsf {OW}\text {-}\mathsf {PCA}\) Security (“Derandomization” + “re-encryption”). \(\mathsf {T}\) is the Encrypt-with-Hash construction from [6]: Starting from an encryption scheme \(\mathsf {PKE}\) and a hash function \(\mathsf {G}\), we build a deterministic encryption scheme \({\mathsf {PKE}}_1=\mathsf {T}[\mathsf {PKE},\mathsf {G}]\) by defining
where \(\mathsf {G}(m)\) is used as the random coins for \(\mathsf {Enc}\). Note that \(\mathsf {Enc}_1\) is deterministic. \({\mathsf {Dec}}_1( sk ,c)\) first decrypts c into \(m'\) and rejects if \(\mathsf {Enc}( pk ,m';\mathsf {G}(m') \ne c\) (“re-encryption”). Modeling \(\mathsf {G}\) as a random oracle, \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\) non-tightly reduces to \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\) and tightly reduces to \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\). If \(\mathsf {PKE}\) furthermore is \(\gamma \)-spread (for sufficiently large \(\gamma \)), then \({\mathsf {PKE}}_1\) is even \(\mathsf {OW}\text {-}\mathsf {PCVA}\) secure. \(\mathsf {OW}\text {-}\mathsf {PCVA}\) securityFootnote 2 is \(\mathsf {PCA}\) security, where the adversary is additionally given access to a validity oracle \(\textsc {Cvo}(c)\) that checks c’s validity (in the sense that it does not decrypt to \(\bot \), see also Definition 1).
\({\mathsf {U}}^{{\not \bot }}\) (\({\mathsf {U}}^\bot \)): from \(\mathsf {OW}\text {-}\mathsf {PCA}\) (\(\mathsf {OW}\text {-}\mathsf {PCVA}\)) to \(\mathsf {IND}\text {-}\mathsf {CCA}\) Security (“Hashing”). Starting from an encryption scheme \({\mathsf {PKE}}_1\) and a hash function \(\mathsf {H}\), we build a key encapsulation mechanism \({\mathsf {KEM}}^{\not \bot }={\mathsf {U}}^{{\not \bot }}[{\mathsf {PKE}}_1,\mathsf {H}]\) with “implicit rejection” by defining
where m is picked at random from the message space.
where \(m := \mathsf {Dec}( sk ,c)\) and s is a random seed which is contained in \( sk \). Modeling \(\mathsf {H}\) as a random oracle, \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\not \bot }\) tightly reduces to \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\).
We also define \({\mathsf {KEM}}^{\bot }={\mathsf {U}}^\bot [{\mathsf {PKE}}_1,\mathsf {H}]\) with “explicit rejection” which differs from \({\mathsf {KEM}}^{\not \bot }\) only in decapsulation:
where \(m:= \mathsf {Dec}( sk ,c)\). Modeling \(\mathsf {H}\) as a random oracle, \(\mathsf {IND}\text {-}\mathsf {CCA}\) of \({\mathsf {KEM}}^{\bot }\) security tightly reduces to \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \({\mathsf {PKE}}_1\). We remark that transformation \({\mathsf {U}}^\bot \) is essentially [20, Table 2], i.e., a KEM variant of the REACT/GEM transformations.
\({\mathsf {U}}^{\not \bot }_\textit{m}\) (\({\mathsf {U}}^{\bot }_{\textit{m}}\)): from deterministic \(\mathsf {OW}\text {-}\mathsf {CPA}\) (\(\mathsf {OW}\text {-}\mathsf {VA}\)) to \(\mathsf {IND}\text {-}\mathsf {CCA}\) Security (“Hashing”). We consider two more variants of \({\mathsf {U}}^{{\not \bot }}\) and \({\mathsf {U}}^\bot \), namely \({\mathsf {U}}^{\not \bot }_\textit{m}\) and \({\mathsf {U}}^{\bot }_{\textit{m}}\). Transformation \({\mathsf {U}}^{\not \bot }_\textit{m}\) (\({\mathsf {U}}^{\bot }_{\textit{m}}\)) is a variant of \({\mathsf {U}}^{{\not \bot }}\) (\({\mathsf {U}}^\bot \)), where \(K=\mathsf {H}(c,m)\) from Eqs. (1)−(3) is replaced by \(K=\mathsf {H}(m)\). We prove that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\not \bot }_\textit{m}:= {\mathsf {U}}^{\not \bot }_\textit{m}[{\mathsf {PKE}}_1,\mathsf {H}]\) (\({\mathsf {KEM}}^{\bot }_\textit{m}:= {\mathsf {U}}^{\bot }_{\textit{m}}[{\mathsf {PKE}}_1,\mathsf {H}]\)) in the random oracle model tightly reduces to \(\mathsf {IND}\text {-}\mathsf {CPA}\) (\(\mathsf {IND}\text {-}\mathsf {VA}\) Footnote 3) security of \({\mathsf {PKE}}_1\), if encryption of \({\mathsf {PKE}}_1\) is deterministic.
\({\mathsf {QU}}^\bot _\textit{m}\): from \(\mathsf {OW}\text {-}\mathsf {PCA}\) to \(\mathsf {IND}\text {-}\mathsf {CCA}\) Security in the Quantum ROM. We first prove that transformation \(\mathsf {T}\) also works in the quantum random oracle model. Next, to go from \(\mathsf {OW}\text {-}\mathsf {PCA}\) to \(\mathsf {IND}\text {-}\mathsf {CCA}\) in the QROM, we build a key encapsulation mechanism \({\mathsf {QKEM}}^\bot _\textit{m}={\mathsf {QU}}^\bot _\textit{m}[{\mathsf {PKE}}_1,\mathsf {H},\mathsf {H}']\) with explicit rejection by defining
where m is picked at random from the message space.
where \(m' := \mathsf {Dec}( sk ,c)\). \({\mathsf {QU}}^\bot _\textit{m}\) differs from \({\mathsf {U}}^{{\not \bot }}\) only in the additional hash value \(d = \mathsf {H}'(m)\) from the ciphertext and \(\mathsf {H}'\) is a random oracle with matching domain and image. This trick was introduced in [40] and used in [38] in the context of the FO transformation. Modeling \(\mathsf {H}\) and \(\mathsf {H}'\) as a quantum random oracles, \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \(\mathsf {KEM}\) reduces to \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\).
The Resulting FO Transformations. Our final transformations \({\mathsf {FO}}^{\not \bot }\) (“FO with implicit rejection”), \({\mathsf {FO}}^\bot \) (“FO with explicit rejection”), \({\mathsf {FO}}^{\not \bot }_\textit{m}\) (“FO with implicit rejection, \(K=\mathsf {H}(m)\)”), \({\mathsf {FO}}^\bot _\textit{m}\) (“FO with explicit rejection, \(K=\mathsf {H}(m)\)”), and \({\mathsf {QFO}}^\bot _\textit{m}\) (“Quantum FO with explicit rejection, \(K=\mathsf {H}(m)\)”) are defined in the following table.

As corollaries of our modular transformation we obtain that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {FO}}^{\not \bot }[\mathsf {PKE},\mathsf {G},\mathsf {H}]\), \({\mathsf {FO}}^\bot [\mathsf {PKE},\mathsf {G},\mathsf {H}]\), \( {\mathsf {FO}}^{\not \bot }_\textit{m}[\mathsf {PKE},\mathsf {G},\mathsf {H}]\), and \({\mathsf {FO}}^\bot _\textit{m}[\mathsf {PKE},\mathsf {G},\mathsf {H}]\) non-tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), and tightly reduces to the \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), in the random oracle model. We remark that transformation \({\mathsf {FO}}^\bot _\textit{m}\) essentially recovers a KEM variant [20, Table 5] of the original FO transformation [23]. Whereas the explicit rejection variants \({\mathsf {FO}}^\bot \) and \({\mathsf {FO}}^\bot _\textit{m}\) require \(\mathsf {PKE}\) to be \(\gamma \)-spread, there is no such requirement on \({\mathsf {FO}}^{\not \bot }\) and \({\mathsf {FO}}^{\not \bot }_\textit{m}\). Further, \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {QFO}}^\bot _\textit{m}[\mathsf {PKE},\mathsf {G},\mathsf {H},\mathsf {H}']\) reduces to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), in the quantum random oracle model. Our transformation \({\mathsf {QFO}}^\bot _\textit{m}\) essentially recovers a KEM variant of the modified FO transformation by Targhi and Unruh [38]. As it is common in the quantum random oracle model, all our reductions are (highly) non-tight. We leave it as an open problem to derive a tighter security reduction of \(\mathsf {T}\), for example to \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\).
Correctness Error. We stress that all our security reductions also take non-zero correctness error into account. Finding the “right” definition of correctness that is achievable (say, by currently proposed lattice-based encryption schemes) and at the same time sufficient to prove security turned out to be a bit subtle. This is the reason why our definition of correctness (see Sect. 2.1) derives from the ones previously given in the literature (e.g. [10, 22]). The concrete bounds of \({\mathsf {FO}}^{\not \bot }\), \({\mathsf {FO}}^\bot \), \({\mathsf {FO}}^{\not \bot }_\textit{m}\), and \({\mathsf {FO}}^\bot _\textit{m}\) give guidance on the required correctness error of the underlying \(\mathsf {PKE}\) scheme. Concretely, for “\(\kappa \) bits security”, \(\mathsf {PKE}\) requires a correctness error of \(2^{-\kappa }\).
Example Instantiations. In the context of ElGamal encryption one can apply \(\{{\mathsf {FO}}^{\not \bot }, {\mathsf {FO}}^\bot , {\mathsf {FO}}^{\not \bot }_\textit{m}, {\mathsf {FO}}^\bot _\textit{m}\}\) to obtain the schemes of [4, 25, 28] whose \(\mathsf {IND}\text {-}\mathsf {CCA}\) security non-tightly reduces to the CDH assumption, and tightly reduces to the DDH assumption. Alternatively, one can directly use \({\mathsf {U}}^{{\not \bot }}\)/\({\mathsf {U}}^\bot \) to obtain the more efficient schemes of [1, 18, 32, 36] whose \(\mathsf {IND}\text {-}\mathsf {CCA}\) security tightly reduces to the gap-DH (a.k.a. strong CDH) assumption. In the context of deterministic encryption schemes such as RSA, Paillier, etc., one can apply \({\mathsf {U}}^{{\not \bot }}\)/\({\mathsf {U}}^\bot \) to obtain schemes mentioned in [20, 36] whose \(\mathsf {IND}\text {-}\mathsf {CCA}\) security tightly reduces to one-way security. Finally, in the context of lattices-based encryption (e.g., [30, 35]), one can apply \({\mathsf {FO}}^{\not \bot }\), \({\mathsf {FO}}^\bot \), \({\mathsf {FO}}^{\not \bot }_\textit{m}\), \({\mathsf {FO}}^\bot _\textit{m}\), and \({\mathsf {QFO}}^\bot _\textit{m}\) to achieve \(\mathsf {IND}\text {-}\mathsf {CCA}\) security.
Transformation \({\mathbf {\mathsf{{S}}}}^{\varvec{\ell }}\) : From OW-CPA to IND-CPA , Tightly. Note that \(\mathsf {T}\) requires \(\mathsf {PKE}\) to be \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure to achieve a tight reduction. In case one has to rely on \(\mathsf {OW}\text {-}\mathsf {CPA}\) security, transformation \({\mathsf {S}}^{\ell }\) offers the following tradeoff between efficiency and tightness. It transforms an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure \(\mathsf {PKE}\) into an \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure \(\mathsf {PKE}_\ell \), where \(\ell \) is a parameter. The ciphertext consists of \(\ell \) independent \(\mathsf {PKE}\) ciphertexts:
The reduction (to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\)) loses a factor of \(q_\mathsf {G}^{1/\ell }\), where \(q_\mathsf {G}\) is the number of \(\mathsf {G}\)-queries an adversary makes.
Observe that the only way to gather information about \(m\) is to explicitly query \(\mathsf {G}(x_1,\dots ,x_n)\), which requires to find all \(x_i\). The reduction can use this observation to embed an \(\mathsf {OW}\text {-}\mathsf {CPA}\) challenge as one \(\mathsf {Enc}( pk ,x_{i^*})\) and hope to learn \(x_{i^*}\) from the \(\mathsf {G}\)-queries of a successful \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary. In this, the reduction will know all \(x_i\) except \(x_{i^*}\). The difficulty in this reduction is to identify the “right” \(\mathsf {G}\)-query (that reveals \(x_{i^*}\)) in all of the adversary’s \(\mathsf {G}\)-queries. Intuitively, the more instances we have, the easier it is for the reduction to spot the \(\mathsf {G}\)-query \((x_1,\dots ,x_\ell )\) (by comparing the \(x_i\) for \(i\ne i^*\)), and the less guessing is necessary. Hence, we get a tradeoff between the number of instances \(\ell \) (and thus the size of the ciphertext) and the loss of the reduction.
1.2 Related Work
As already pointed out, \({\mathsf {FO}}^\bot _\textit{m}= {\mathsf {U}}^{\bot }_{\textit{m}}\circ \mathsf {T}\) is essentially a KEM variant of the Fujisaki-Okamoto transform from [20, Table 5]. Further, \({\mathsf {U}}^\bot \) is a KEM variant [20] of the GEM/REACT transform [1, 18, 32]. Our modular view suggest that the FO transform implicitly contains the GEM/REACT transform, at least the proof technique. With this more general view, the FO transform and its variants remains the only known transformation from \(\mathsf {CPA}\) to \(\mathsf {CCA}\) security. It is an interesting open problem to come up with alternative transformations that get rid of derandomization or that dispense with re-encryption (which preserving efficiency). Note that for the ElGamal encryption scheme, the “twinning” technique [15, 16] does exactly this, but it uses non-generic zero-knowledge proofs that are currently not available for all schemes (e.g., for lattice-based schemes).
In concurrent and independent work, [2] considers the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \(\mathsf {LIMA}\) which in our notation can be described as \({\mathsf {FO}}^\bot _\textit{m}[\mathsf {RLWE},\mathsf {G},\mathsf {H}]\). Here \(\mathsf {RLWE}\) is a specific encryption scheme based on lattices associated to polynomial rings from [29], which is \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure under the Ring-LWE assumption. As the main result, [2] provides a tight reduction of \(\mathsf {LIMA}\)’s \(\mathsf {IND}\text {-}\mathsf {CCA}\) security to the Ring-LWE assumption, in the random oracle model. The proof exploits “some weakly homomorphic properties enjoyed by the underlying encryption scheme” and therefore does not seem to be applicable to other schemes. The tight security reduction from Ring-LWE is recovered as a special case of our general security results on \({\mathsf {FO}}^\bot _\textit{m}\). We note that the security reduction of [2] does not take the (non-zero) correctness error of \(\mathsf {RLWE}\) into account.
2 Preliminaries
For \(n \in \mathbb {N}\), let \([n] := \lbrace 1, \dots , n \rbrace .\) For a set S, |S| denotes the cardinality of S. For a finite set S, we denote the sampling of a uniform random element x by  , while we denote the sampling according to some distribution \(\mathfrak {D}\) by \(x \leftarrow \mathfrak {D}\). For a polynomial p(X) with integer coefficients, we denote by \(\mathsf {Roots}(p)\) the (finite) set of (complex) roots of p. By \(\llbracket B\rrbracket \) we denote the bit that is 1 if the Boolean Statement B is true, and otherwise 0.
, while we denote the sampling according to some distribution \(\mathfrak {D}\) by \(x \leftarrow \mathfrak {D}\). For a polynomial p(X) with integer coefficients, we denote by \(\mathsf {Roots}(p)\) the (finite) set of (complex) roots of p. By \(\llbracket B\rrbracket \) we denote the bit that is 1 if the Boolean Statement B is true, and otherwise 0.
Algorithms. We denote deterministic computation of an algorithm A on input x by \(y := A(x).\) We denote algorithms with access to an oracle \(\textsc {O}\) by \(\mathsf {A}^{\textsc {O}}\). Unless stated otherwise, we assume all our algorithms to be probabilistic and denote the computation by \(y\leftarrow A(x)\).
Random Oracles. We will at times model hash functions \(\mathsf {H}: \mathfrak {D}_\mathsf {H}\rightarrow \mathfrak {I}(\mathsf {H})\) as random oracles. To keep record of the queries issued to \(\mathsf {H}\), we will use a hash list \(\mathfrak {L}_{\mathsf {H}}\) that contains all tuples \((x,\mathsf {H}(x))\) of arguments \(x \in \mathfrak {D}_\mathsf {H}\) that \(\mathsf {H}\) was queried on and the respective answers \(\mathsf {H}(x)\). We make the convention that \(\mathsf {H}(x)=\bot \) for all \(x \not \in \mathfrak {D}_\mathsf {H}\).
Games. Following [8, 37], we use code-based games. We implicitly assume boolean flags to be initialized to false, numerical types to 0, sets to \(\emptyset \), and strings to the empty string \(\epsilon \). We make the convention that a procedure terminates once it has returned an output.
2.1 Public-Key Encryption
Syntax. A public-key encryption scheme \(\mathsf {PKE}= (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) consists of three algorithms and a finite message space \(\mathcal {M}\) (which we assume to be efficiently recognizable). The key generation algorithm \(\mathsf {Gen}\) outputs a key pair \(( pk , sk )\), where \( pk \) also defines a randomness space \(\mathcal {R}=\mathcal {R}( pk )\). The encryption algorithm \(\mathsf {Enc}\), on input \( pk \) and a message \(m \in \mathcal {M}\), outputs an encryption \(c \leftarrow \mathsf {Enc}( pk ,m)\) of m under the public key \( pk \). If necessary, we make the used randomness of encryption explicit by writing \(c := \mathsf {Enc}( pk ,m; r)\), where  and \(\mathcal {R}\) is the randomness space. The decryption algorithm \(\mathsf {Dec}\), on input \( sk \) and a ciphertext c, outputs either a message \(m = \mathsf {Dec}( sk ,c) \in \mathcal {M}\) or a special symbol \( \bot \notin \mathcal {M}\) to indicate that c is not a valid ciphertext.
and \(\mathcal {R}\) is the randomness space. The decryption algorithm \(\mathsf {Dec}\), on input \( sk \) and a ciphertext c, outputs either a message \(m = \mathsf {Dec}( sk ,c) \in \mathcal {M}\) or a special symbol \( \bot \notin \mathcal {M}\) to indicate that c is not a valid ciphertext.
Correctness. We call a public-key encryption scheme \(\mathsf {PKE}\) \(\delta \)-correct if
where the expectation is taken over \(( pk , sk ) \leftarrow \mathsf {Gen}\). Equivalently, \(\delta \)-correctness means that for all (possibly unbounded) adversaries \(\mathsf {A}\), \(\Pr [\mathsf {COR}^\mathsf {A}_\mathsf {PKE}\Rightarrow 1] \le \delta \), where the correctness game \(\mathsf {COR}\) is defined as in Fig. 2 (left). That is, an (unbounded) adversary obtains the public and the secret key and wins if it finds a message inducing a correctness error. Note that our definition of correctness slightly derives from previous definitions (e.g. [10, 22]) but it has been carefully crafted such that it is sufficient to prove our main theorems (i.e., the security of the Fujisaki-Okamoto transformation) and at the same time it is fulfilled by all recently proposed lattice-based encryption schemes with correctness error.
If \(\mathsf {PKE}= \mathsf {PKE}^\mathsf {G}\) is defined relative to a random oracle \(\mathsf {G}\), then defining correctness is a bit more subtle as the correctness bound might depend on the number of queries to \(\mathsf {G}\).Footnote 4 We call a public-key encryption scheme \(\mathsf {PKE}\) in the random oracle model \(\delta (q_\mathsf {G})\)-correct if for all (possibly unbounded) adversaries \(\mathsf {A}\) making at most \(q_\mathsf {G}\) queries to random oracle \(\mathsf {G}\), \(\Pr [\mathsf {COR}\text {-}\mathsf {RO}^\mathsf {A}_\mathsf {PKE}\Rightarrow 1] \le \delta (q_\mathsf {G})\), where the correctness game \(\mathsf {COR}\text {-}\mathsf {RO}\) is defined as in Fig. 2 (right). If \(\mathsf {PKE}\) is defined relative to two random oracles \(\mathsf {G}\), \(\mathsf {H}\), then the correctness error \(\delta \) is a function in \(q_\mathsf {G}\) and \(q_\mathsf {H}\).
Note that our correctness definition in the standard model is a special case of the one in the random oracle model, where the number of random oracle queries is zero and hence \(\delta (q_\mathsf {G})\) is a constant.
Min-Entropy. [24] For \(( pk , sk ) \leftarrow \mathsf {Gen}\) and \(m \in \mathcal {M}\), we define the min-entropy of \(\mathsf {Enc}( pk ,m)\) by \( \gamma (pk, m):= - \log \max _{c \in \mathcal {C}} \Pr _{r \leftarrow \mathcal {R}} \left[ c = \mathsf {Enc}( pk ,m; r) \right] \). We say that \(\mathsf {PKE}\) is \(\gamma \)-spread if, for every key pair \(( pk , sk ) \leftarrow \mathsf {Gen}\) and every message \(m \in \mathcal {M}\), \(\gamma ( pk , m) \ge \gamma \). In particular, this implies that for every possible ciphertext \(c \in \mathcal {C}\), \(\Pr _{r \leftarrow \mathcal {R}} \left[ c = \mathsf {Enc}( pk ,m;r) \right] \le {2^{-\gamma }}\).
Security. We now define three security notions for public-key encryption: One-Wayness under Chosen Plaintext Attacks (\(\mathsf {OW}\text {-}\mathsf {CPA}\)), One-Wayness under Plaintext Checking Attacks (\(\mathsf {OW}\text {-}\mathsf {PCA}\)) and One-Wayness under Plaintext and Validity Checking Attacks (\(\mathsf {OW}\text {-}\mathsf {PCVA}\)).
Definition 1
(\(\mathsf {OW}\text {-}\mathsf {ATK}\)). Let \(\mathsf {PKE}=(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a public-key encryption scheme with message space \(\mathcal {M}\). For \(\mathsf {ATK}\in \lbrace \mathsf {CPA}, \mathsf {PCA}, \mathsf {VA}, \mathsf {PCVA}\rbrace \), we define \(\mathsf {OW}\text {-}\mathsf {ATK}\) games as in Fig. 3, where
We define the \(\mathsf {OW}\text {-}\mathsf {ATK}\) advantage function of an adversary \(\mathsf {A}\) against \(\mathsf {PKE}\) as \(\mathrm {Adv}^{\mathsf {OW}\text {-}\mathsf {ATK}}_{\mathsf {PKE}}(\mathsf {A}) := \Pr [\mathsf {OW}\text {-}\mathsf {ATK}^{\mathsf {A}}_\mathsf {PKE}\Rightarrow 1 ]\).
Games \(\mathsf {OW}\text {-}\mathsf {ATK}\) (\(\mathsf {ATK}\in \lbrace \mathsf {CPA}, \mathsf {PCA}, \mathsf {VA}, \mathsf {PCVA}\rbrace \)) for \(\mathsf {PKE}\), where \(\textsc {O}_\mathsf {ATK}\) is defined in Definition 1. \(\textsc {Pco}(\cdot ,\cdot )\) is the Plaintext Checking Oracle and \(\textsc {Cvo}(\cdot )\) is the Ciphertext Validity Oracle.
A few remarks are in place. Our definition of the plaintext checking oracle \(\textsc {Pco}(m,c)\) (c.f. Fig. 3) implicitly disallows queries on messages \(m \in \mathcal {M}\). (With the convention that \(\textsc {Pco}(m \not \in \mathcal {M},c)\) yields \(\bot \).) This restriction is important since otherwise the ciphertext validity oracle \(\textsc {Cvo}(\cdot )\) could be simulated as \(\textsc {Cvo}(m) = \textsc {Pco}(\bot ,c)\). Similarly, the ciphertext validity oracle \(\textsc {Cvo}(c)\) implicitly disallows queries on the challenge ciphertext \(c^*\).
Usually, the adversary wins the one-way game iff its output \(m'\) equals the challenge message \(m^*\). Instead, in game \(\mathsf {OW}\text {-}\mathsf {ATK}\) the correctness of \(m'\) is checked using the \(\textsc {Pco}\) oracle, i.e., it returns 1 iff \(\mathsf {Dec}( sk ,c^*)=m'\). The two games have statistical difference \(\delta \), if \(\mathsf {PKE}\) is \(\delta \)-correct.
Additionally, we define Indistinguishability under Chosen Plaintext Attacks (\(\mathsf {IND}\text {-}\mathsf {CPA}\)).
Definition 2
(\(\mathsf {IND}\text {-}\mathsf {CPA}\)). Let \(\mathsf {PKE}=(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a public-key encryption scheme with message space \(\mathcal {M}\). We define the \(\mathsf {IND}\text {-}\mathsf {CPA}\) game as in Fig. 4, and the \(\mathsf {IND}\text {-}\mathsf {CPA}\) advantage function of an adversary \(\mathsf {A}= (\mathsf {A}_1, \mathsf {A}_2)\) against \(\mathsf {PKE}\) (such that \(\mathsf {A}_2\) has binary output) as  .
.
We also define \(\mathsf {OW}\text {-}\mathsf {ATK}\) and \(\mathsf {IND}\text {-}\mathsf {CPA}\) security in the random oracle model, where \(\mathsf {PKE}\) and adversary \(\mathsf {A}\) are given access to a random oracle \(\mathsf {H}\). We make the convention that the number \(q_\mathsf {H}\) of the adversary’s random oracle queries count the total number of times \(\mathsf {H}\) is executed in the experiment. That is, the number of \(\mathsf {A}\) explicit queries to \(\mathsf {H}(\cdot )\) plus the number of implicit queries to \(\mathsf {H}(\cdot )\) made by the experiment.
It is well known that \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\) with sufficiently large message space implies its \(\mathsf {OW}\text {-}\mathsf {CPA}\) security.
Lemma 1
For any adversary \(\mathsf {B}\) there exists an adversary \(\mathsf {A}\) with the same running time as that of \(\mathsf {B}\) such that  .
.
2.2 Key Encapsulation
Syntax. A key encapsulation mechanism \(\mathsf {KEM}= (\mathsf {Gen}, \mathsf {Encaps}, \mathsf {Decaps})\) consists of three algorithms. The key generation algorithm \(\mathsf {Gen}\) outputs a key pair \(( pk , sk )\), where \( pk \) also defines a finite key space \(\mathcal {K}\). The encapsulation algorithm \(\mathsf {Encaps}\), on input \( pk \), outputs a tuple (K, c) where c is said to be an encapsulation of the key K which is contained in key space \(\mathcal {K}\). The deterministic decapsulation algorithm \(\mathsf {Decaps}\), on input \( sk \) and an encapsulation c, outputs either a key \(K := \mathsf {Decaps}( sk , c) \in \mathcal {K}\) or a special symbol \( \bot \notin \mathcal {K}\) to indicate that c is not a valid encapsulation. We call \(\mathsf {KEM}\) \(\delta \)-correct if
Note that the above definition also makes sense in the random oracle model since KEM ciphertexts do not depend on messages.
Security. We now define a security notion for key encapsulation: Indistinguishbility under Chosen Ciphertext Attacks (\(\mathsf {IND}\text {-}\mathsf {CCA}\)).
Definition 3
(\(\mathsf {IND}\text {-}\mathsf {CCA}\)). We define the \(\mathsf {IND}\text {-}\mathsf {CCA}\) game as in Fig. 4 and the \(\mathsf {IND}\text {-}\mathsf {CCA}\) advantage function of an adversary \(\mathsf {A}\) (with binary output) against
\(\mathsf {KEM}\) as  .
.
3 Modular FO Transformations
In Sect. 3.1, we will introduce \(\mathsf {T}\) that transforms any \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure encryption scheme \(\mathsf {PKE}\) into a \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure encryption scheme \({\mathsf {PKE}}_1\). If \(\mathsf {PKE}\) is furthermore \(\mathsf {IND}\text {-}\mathsf {CPA}\), then the reduction is tight. Furthermore, if \(\mathsf {PKE}\) is \(\gamma \)-spread, then \({\mathsf {PKE}}_1\) even satisfied the stronger security notion of \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security. Next, in Sect. 3.2, we will introduce transformations \({\mathsf {U}}^{{\not \bot }}\), \({\mathsf {U}}^{\not \bot }_\textit{m}\) (\({\mathsf {U}}^\bot \), \({\mathsf {U}}^{\bot }_{\textit{m}}\)) that transform any \(\mathsf {OW}\text {-}\mathsf {PCA}\) (\(\mathsf {OW}\text {-}\mathsf {PCVA}\)) secure encryption scheme \({\mathsf {PKE}}_1\) into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure \(\mathsf {KEM}\). The security reduction is tight. Transformations \({\mathsf {U}}^{\not \bot }_\textit{m}\) and \({\mathsf {U}}^{\bot }_{\textit{m}}\) can only be applied for deterministic encryption schemes. Combining \(\mathsf {T}\) with \(\{{\mathsf {U}}^{{\not \bot }},{\mathsf {U}}^{\not \bot }_\textit{m}, {\mathsf {U}}^\bot , {\mathsf {U}}^{\bot }_{\textit{m}}\}\), in Sect. 3.3 we provide concrete bounds for the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of the resulting KEMs. Finally, in Sect. 3.4 we introduce \({\mathsf {S}}^{\ell }\) that transforms any \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure scheme into an \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure one, offering a tradeoff between tightness and ciphertext size.
3.1 Transformation \(\mathsf {T}\): From \(\mathsf {OW}\text {-}\mathsf {CPA}\)/\(\mathsf {IND}\text {-}\mathsf {CPA}\) to \(\mathsf {OW}\text {-}\mathsf {PCVA}\)
\(\mathsf {T}\) transforms an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure public-key encryption scheme into an \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure one.
The Construction. To a public-key encryption scheme \(\mathsf {PKE}= (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) with message space \(\mathcal {M}\) and randomness space \(\mathcal {R}\), and random oracle \(\mathsf {G}: \mathcal {M}\rightarrow \mathcal {R}\), we associate \(\mathsf {PKE}_1= \mathsf {T}[\mathsf {PKE},\mathsf {G}]\). The algorithms of \(\mathsf {PKE}_1=(\mathsf {Gen},\mathsf {Enc}_1,\mathsf {Dec}_1)\) are defined in Fig. 5. Note that \(\mathsf {Enc}_1\) deterministically computers the ciphertext as \(c := \mathsf {Enc}( pk ,m; \mathsf {G}(m))\).
Non-tight Security from \(\mathsf {OW}\text {-}\mathsf {CPA}\). The following theorem establishes that \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \({\mathsf {PKE}}_1\) (cf. Definition 1) non-tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), in the random oracle model, given that \(\mathsf {PKE}\) is \(\gamma \)-spread (for sufficiently large \(\gamma \)). If \(\mathsf {PKE}\) is not \(\gamma \)-spread, then \(\mathsf {PKE}_1\) is still \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure.
Theorem 1
(
 ). If \(\mathsf {PKE}\) is \(\delta \)-correct, then \(\mathsf {PKE}_1\) is \(\delta _1\)-correct in the random oracle model with \(\delta _1(q_\mathsf {G})=q_\mathsf {G}\cdot \delta \). Assume \(\mathsf {PKE}\) to be \(\gamma \)-spread. Then, for any \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the random oracle \(\mathsf {G}\), \(q_P\) queries to a plaintext checking oracle \(\textsc {Pco}\), and \(q_V\) queries to a validity checking oracle \(\textsc {Cvo}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
). If \(\mathsf {PKE}\) is \(\delta \)-correct, then \(\mathsf {PKE}_1\) is \(\delta _1\)-correct in the random oracle model with \(\delta _1(q_\mathsf {G})=q_\mathsf {G}\cdot \delta \). Assume \(\mathsf {PKE}\) to be \(\gamma \)-spread. Then, for any \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the random oracle \(\mathsf {G}\), \(q_P\) queries to a plaintext checking oracle \(\textsc {Pco}\), and \(q_V\) queries to a validity checking oracle \(\textsc {Cvo}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
The main idea of the proof is that since \(\mathsf {Enc}_1\) is deterministic, the \(\mathsf {PCA}(\cdot ,\cdot )\) oracle can be equivalently implemented by “re-encryption” and the \(\textsc {Cvo}(\cdot )\) oracle by controlling the random oracles. Additional care has to be taken to account for the correctness error.
Proof
To prove correctness, consider an adversary \(\mathsf {A}\) playing the correctness game \(\mathsf {COR}\text {-}\mathsf {RO}\) (Fig. 2) of \(\mathsf {PKE}_1\) in the random oracle model. Game \(\mathsf {COR}\text {-}\mathsf {RO}\) makes at most \(q_{\mathsf {G}}\) (distinct) queries \(\mathsf {G}(m_1),\dots ,\mathsf {G}(m_{q_\mathsf {G}})\) to \(\mathsf {G}\). We call such a query \(\mathsf {G}(m_i)\) problematic iff it exhibits a correctness error in \(\mathsf {PKE}_1\) (in the sense that \(\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m_i;\mathsf {G}(m_i)))\ne m_i\)). Since \(\mathsf {G}\) outputs independently random values, each \(\mathsf {G}(m_i)\) is problematic with probability at most \(\delta \) (averaged over \(( pk , sk )\)), since we assumed that \(\mathsf {PKE}\) is \(\delta \)-correct. Hence, a union bound shows that the probability that at least one \(\mathsf {G}(m_i)\) is problematic is at most \(q_\mathsf {G}\cdot \delta \). This proves \(\Pr [\mathsf {COR}\text {-}\mathsf {RO}^\mathsf {A}\Rightarrow 1] \le q_\mathsf {G}\cdot \delta \) and hence \(\mathsf {PKE}_1\) is \(\delta _1\)-correct with \(\delta _1(q_\mathsf {G})=q_\mathsf {G}\cdot \delta \).
To prove security, let \(\mathsf {B}\) be an adversary against the \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \(\mathsf {PKE}_1\), issuing at most \(q_{\mathsf {G}}\) queries to \(\mathsf {G}\), at most \(q_{P}\) queries to \(\textsc {Pco}\), and at most \(q_V\) queries to \(\textsc {Cvo}\). Consider the sequence of games given in Fig. 6.
Games \(G_0\)-\(G_3\) for the proof of Theorem 1.
Game \(G_0\). This is the original \(\mathsf {OW}\text {-}\mathsf {PCVA}\) game. Random oracle queries are stored in set \(\mathfrak {L}_{G}\) with the convention that \(\mathsf {G}(m) = r\) iff \((m,r) \in \mathfrak {L}_{G}\). Hence,
Game \(G_1\). In game \(G_1\) the ciphertext validity oracle \(\textsc {Cvo}(c \ne c^*)\) is replaced with one that first computes \(m' = \mathsf {Dec}( sk ,c)\) and returns 1 iff there exists a previous query (m, r) to \(\mathsf {G}\) such that \(\mathsf {Enc}( pk ,m; r) = c\) and \(m=m'\).
Consider a single query \(\textsc {Cvo}(c)\) and define \(m':=\mathsf {Dec}( sk ,c)\). If \(\textsc {Cvo}(c)=1\) in \(G_1\), then \(\mathsf {G}(m')=\mathsf {G}(m)=r\) and hence \(\mathsf {Enc}( pk ,m'; G(m'))=c\), meaning \(\textsc {Cvo}(c)=1\) in \(G_0\). If \(\textsc {Cvo}(c)=1\) in \(G_0\), then we can only have \(\textsc {Cvo}(c)=0\) in \(G_1\) only if \(\mathsf {G}(m')\) was not queried before. This happens with probability \(2^{-\gamma }\), where \(\gamma \) is the parameter from the \(\gamma \)-spreadness of \(\mathsf {PKE}\). By the union bound we obtain
Game \(G_2\). In game \(G_2\) we replace the plaintext checking oracle \(\textsc {Pco}(m,c)\) and the ciphertext validity oracle \(\textsc {Cvo}(c)\) by a simulation that does not check whether \(m = m'\) anymore, where \(m'=\mathsf {Dec}( sk ,c)\)
We claim
To show Eq. (4), observe that the whole Game \(G_1\) (and also the whole Game \(G_2\)) makes at most \(q_{\mathsf {G}}\) (distinct) queries \(\mathsf {G}(m_1),\dots ,\mathsf {G}(m_{q_\mathsf {G}})\) to \(\mathsf {G}\). Again, we call such a query \(\mathsf {G}(m_i)\) problematic iff it exhibits a correctness error in \(\mathsf {PKE}_1\) (in the sense that \(\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m_i;\mathsf {G}(m_i)))\ne m_i\)). Clearly, if \(\mathsf {B}\) makes a problematic query, then there exists an adversary \(\mathsf {F}\) that wins the correctness game \(\mathsf {COR}\text {-}\mathsf {RO}\) in the random oracle model. Hence, the probability that at least one \(\mathsf {G}(m_i)\) is problematic is at most \(\delta _1(q_\mathsf {G})\le q_\mathsf {G}\cdot \delta \).
However, conditioned on the event that no query \(\mathsf {G}(m_i)\) is problematic, Game \(G_1\) and Game \(G_2\) proceed identically (cf. Fig. 6). Indeed, the two games only differ if \(\mathsf {B}\) submits a \(\textsc {Pco}\) query \((m,c)\) or a \(\textsc {Cvo}\) query c together with a \(\mathsf {G}\) query m such that \(\mathsf {G}(m)\) is problematic and \(c=\mathsf {Enc}( pk ,m;\mathsf {G}(m))\). (In this case, \(G_1\) will answer the query with \(0\), while \(G_2\) will answer with \(1\).) This shows Eq. (4).
Game \(G_3\). In Game \(G_3\), we add a flag \(\textsc {QUERY}\) in line 09 and abort when it is raised. Hence, \(G_2\) and \(G_3\) only differ if \(\textsc {QUERY}\) is raised, meaning that \(\mathsf {B}\) made a query \(\mathsf {G}\) on \(m^*\), or, equivalently, \((m^*,\cdot ) \in \mathfrak {L}_{G}\). Due to the difference lemma [37],
We first bound \(\Pr [G_3^{\mathsf {B}} \Rightarrow 1]\) by constructing an adversary \(\mathsf {C}\) in Fig. 7 against the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of the original encryption scheme \(\mathsf {PKE}\). \(\mathsf {C}\) inputs \(( pk ,c^* \leftarrow \mathsf {Enc}( pk ,m^*))\) for random, unknown \(m^*\), perfectly simulates game \(G_3\) for \(\mathsf {B}\), and finally outputs \(m'=m^*\) if \(\mathsf {B}\) wins in game \(G_3\).
So far we have established the bound
Finally, in Fig. 7 we construct an adversary \(\mathsf {D}\) against the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of the original encryption scheme \(\mathsf {PKE}\), that inputs \(( pk ,c^* \leftarrow \mathsf {Enc}( pk ,m^*))\), perfectly simulates game \(G_3\) for \(\mathsf {B}\). If flag \(\textsc {QUERY}\) is set in \(G_3\) then there exists en entry \((m^*,\cdot ) \in \mathfrak {L}_{\mathsf {G}}\) and \(\mathsf {D}\) returns the correct \(m'=m^*\) with probability at most \(1/q_{\mathsf {G}}\). We just showed
Combining the latter bound with Eq. (5) and folding \(\mathsf {C}\) and \(\mathsf {D}\) into one single adversary \(\mathsf {A}\) against \(\mathsf {OW}\text {-}\mathsf {CPA}\) yields the required bound of the theorem.
By definition, \(\mathsf {OW}\text {-}\mathsf {PCA}\) security is \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security with \(q_V:=0\) queries to the validity checking oracle. Hence, the bound of Theorem 1 shows that \(\mathsf {PKE}_1\) is in particular \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure, without requiring \(\mathsf {PKE}\) to be \(\gamma \)-spread.
Tight Security from \(\mathsf {IND}\text {-}\mathsf {CPA}\). Whereas the reduction to \(\mathsf {OW}\text {-}\mathsf {CPA}\) security in Theorem 1 was non-tight, the following theorem establishes that \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \(\mathsf {PKE}_1\) tightly reduces to \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), in the random oracle model, given that \(\mathsf {PKE}\) is \(\gamma \)-spread. If \(\mathsf {PKE}\) is not \(\gamma \)-spread, then \(\mathsf {PKE}_1\) is still \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure.
Theorem 2
(
 ). Assume \(\mathsf {PKE}\) to be \(\delta \)-correct and \(\gamma \)-spread. Then, for any \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the random oracle \(\mathsf {G}\), \(q_P\) queries to a plaintext checking oracle \(\textsc {Pco}\), and \(q_V\) queries to a validity checking oracle \(\textsc {Cvo}\), there exists an \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
). Assume \(\mathsf {PKE}\) to be \(\delta \)-correct and \(\gamma \)-spread. Then, for any \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the random oracle \(\mathsf {G}\), \(q_P\) queries to a plaintext checking oracle \(\textsc {Pco}\), and \(q_V\) queries to a validity checking oracle \(\textsc {Cvo}\), there exists an \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
Proof
Considering the games of Fig. 6 from the proof of Theorem 1 we obtain by Eq. (5)
where the last inequation uses Lemma 1.
Adversary \(\mathsf {D}= (\mathsf {D}_1, \mathsf {D}_2)\) against \(\mathsf {IND}\text {-}\mathsf {CPA}\) for the proof of Theorem 2. For fixed \(m \in \mathcal {M}\), \(\mathfrak {L}_{G}(m)\) is the set of all \((m,r) \in \mathfrak {L}_{G}\). Oracles \(\textsc {Pco}\), \(\textsc {Cvo}\) are defined as in game \(G_3\), and \(\mathsf {G}\) is defined as in game \(G_2\) of Fig. 6.
In Fig. 8 we construct an adversary \(\mathsf {D}=(\mathsf {D}_1,\mathsf {D}_2)\) against the \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of the original encryption scheme \(\mathsf {PKE}\) that wins if flag \(\textsc {QUERY}\) is set in \(G_3\). The first adversary \(\mathsf {D}_1\) picks two random messages \(m_0^*, m_1^*\). The second adversary \(\mathsf {D}_2\) inputs \(( pk ,c^* \leftarrow \mathsf {Enc}( pk ,m_b^*), st )\), for an unknown random bit b, and runs \(\mathsf {B}\) on \(( pk ,c^*)\), simulating its view in game \(G_3\). Note that by construction message \(m^*_b\) is uniformly distributed.
Consider game \(\mathsf {IND}\text {-}\mathsf {CPA}^\mathsf {D}\) with random challenge bit b. Let \(\textsc {BADG}\) be the event that \(\mathsf {B}\) queries random oracle \(\mathsf {G}\) on \(m^*_{1-b}\). Since \(m^*_{1-b}\) is uniformly distributed and independent from \(\mathsf {B}\)’s view, we have \(\Pr [\textsc {BADG}] \le q_\mathsf {G}/|\mathcal {M}|\). For the remainder of the proof we assume \(\textsc {BADG}\) did not happen, i.e. \(|\mathfrak {L}_{G}(m^*_{1-b})| = 0\).
If \(\textsc {QUERY}\) happens, then \(\mathsf {B}\) queried the random oracle \(\mathsf {G}\) on \(m^*_b\), which implies \(|\mathfrak {L}_{G}(m^*_b)| > 0 = |\mathfrak {L}_{G}(m^*_{1-b})|\) and therefore \(b=b'\). If \(\textsc {QUERY}\) does not happen, then \(\mathsf {B}\) did not query random oracle \(\mathsf {G}\) on \(m^*_b\). Hence, \(|\mathfrak {L}_{G}(m^*_b)| = |\mathfrak {L}_{G}(m^*_{1-b})|=0\) and \(\Pr [b=b']=1/2\) since \(\mathsf {A}\) picks a random bit \(b'\). Overall, we have
Folding \(\mathsf {C}\) and \(\mathsf {D}\) into one single \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) yields the required bound of the theorem.
With the same argument as in Theorem 1, a tight reduction to \(\mathsf {OW}\text {-}\mathsf {PCA}\) security is implied without requiring \(\mathsf {PKE}\) to be \(\gamma \)-spread.
3.2 Transformations \({\mathsf {U}}^{{\not \bot }}\), \({\mathsf {U}}^{\not \bot }_\textit{m}\), \({\mathsf {U}}^\bot \), \({\mathsf {U}}^{\bot }_{\textit{m}}\)
In this section we introduce four variants of a transformation \(\mathsf {U}\), namely \({\mathsf {U}}^{{\not \bot }}\), \({\mathsf {U}}^{\not \bot }_\textit{m}\), \({\mathsf {U}}^\bot \), \({\mathsf {U}}^{\bot }_{\textit{m}}\), that convert a public-key encryption scheme \({\mathsf {PKE}}_1\) into a key encapsulation mechanism \(\mathsf {KEM}\). Their differences are summarized in the following table.

Transformation \({\mathbf {\mathsf{{U}}}}^{\varvec{\bot }}\) : From OW-PVCA to IND-CCA. \({\mathsf {U}}^\bot \) transforms an \(\mathsf {OW}\text {-}\mathsf {PCVA}\) secure public-key encryption scheme into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key encapsulation mechanism. The \(^\bot \) in \({\mathsf {U}}^\bot \) means that decapsulation of an invalid ciphertext results in the rejection symbol \(\bot \) (“explicit rejection”).
The Construction. To a public-key encryption scheme \({\mathsf {PKE}}_1= ({\mathsf {Gen}}_1, \mathsf {Enc}_1, {\mathsf {Dec}}_1)\) with message space \(\mathcal {M}\), and a hash function \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\), we associate \({\mathsf {KEM}}^{\bot }= {\mathsf {U}}^\bot [{\mathsf {PKE}}_1,\mathsf {H}]\). The algorithms of \({\mathsf {KEM}}^{\bot }=({\mathsf {Gen}}_1,\mathsf {Encaps},{\mathsf {Decaps}}^{\bot })\) are defined in Fig. 9.
Security. The following theorem establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\bot }\) tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \({\mathsf {PKE}}_1\), in the random oracle model.
Theorem 3
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, so is \({\mathsf {KEM}}^{\bot }\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\bot }\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{\bot }\) and at most \(q_{\mathsf {H}}\) queries to the random oracle \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_{\mathsf {H}}\) queries both to the \(\textsc {Pco}\) oracle and to the \(\textsc {Cvo}\) oracle such that
). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, so is \({\mathsf {KEM}}^{\bot }\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\bot }\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{\bot }\) and at most \(q_{\mathsf {H}}\) queries to the random oracle \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {PCVA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_{\mathsf {H}}\) queries both to the \(\textsc {Pco}\) oracle and to the \(\textsc {Cvo}\) oracle such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
The main idea of the proof is to simulate the decapsulation oracle without the secret-key. This can be done by answering decryption queries with a random key and then later patch the random oracle using the plaintext checking oracle \(\textsc {Pco}(\cdot ,\cdot )\) provided by the \(\mathsf {OW}\text {-}\mathsf {PCVA}\) game. Additionally, the ciphertext validity oracle \(\textsc {Cvo}(\cdot )\) is required to reject decapsulation queries with inconsistent ciphertexts.
Games \(G_0\) - \(G_2\) for the proof of Theorem 3.
Proof
It is easy to verify the correctness bound. Let \(\mathsf {B}\) be an adversary against the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\bot }\), issuing at most \(q_D\) queries to \({\textsc {Decaps}}^{\bot }\) and at most \(q_{\mathsf {H}}\) queries to \(\mathsf {H}\). Consider the games given in Fig. 10.
Game \(G_0\). Since game \(G_0\) is the original \(\mathsf {IND}\text {-}\mathsf {CCA}\) game,
Game \(G_1\). In game \(G_1\), the oracles \(\mathsf {H}\) and \({\textsc {Decaps}}^{\bot }\) are modified such that they make no use of the secret key any longer except by testing if \({\mathsf {Dec}}_1( sk ',c)=m\) for given (m, c) in line 15 and if \({\mathsf {Dec}}_1( sk ,c) \in \mathcal {M}\) for given c in line 27. Game \(G_1\) contains two sets: hash list \(\mathfrak {L}_{H}\) that contains all entries (m, c, K) where \(\mathsf {H}\) was queried on (m, c), and set \(\mathfrak {L}_{D}\) that contains all entries (c, K) where either \(\mathsf {H}\) was queried on \((m',c)\), \(m' := {\mathsf {Dec}}_1( sk ', c)\), or \({\textsc {Decaps}}^{\bot }\) was queried on c. In order to show that the view of \(\mathsf {B}\) is identical in games \(G_0\) and \(G_1\), consider the following cases for a fixed ciphertext c and \(m' := {\mathsf {Dec}}_1( sk ', c)\).
-
Case 1: \(m' \notin \mathcal {M}\). Since \(\textsc {Cvo}(c)=0\) is equivalent to \(m'=\bot \), \({\textsc {Decaps}}^{\bot }(c)\) returns \(\bot \) as in both games.
-
Case 2: \(m' \in \mathcal {M}.\) We will now show that \(\mathsf {H}\) in game \(G_1\) is “patched”, meaning that it is ensures \({\textsc {Decaps}}^{\bot }(c) = \mathsf {H}(m',c)\), where \(m' := {\mathsf {Dec}}_1( sk ,c)\), for all ciphertexts c with \(m' \in \mathcal {M}\). We distinguish two sub-cases: \(\mathsf {B}\) might either first query \(\mathsf {H}\) on \((m',c)\), then \({\textsc {Decaps}}^{\bot }\) on c, or the other way round.
-
If \(\mathsf {H}\) is queried on \((m',c)\) first, it is recognized that \({\mathsf {Dec}}_1( sk ,c)=m\) in line 15. Since \(\textsc {Decaps}\) was not yet queried on c, no entry of the form (c, K) can already exist in \(\mathfrak {L}_{D}\). Therefore, besides adding
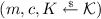 to \(\mathfrak {L}_{H}\), \(\mathsf {H}\) also adds (c, K) to \(\mathfrak {L}_{D}\) in line 22, thereby defining \({\textsc {Decaps}}^{\bot }(c) := K = \mathsf {H}(m',c)\).
to \(\mathfrak {L}_{H}\), \(\mathsf {H}\) also adds (c, K) to \(\mathfrak {L}_{D}\) in line 22, thereby defining \({\textsc {Decaps}}^{\bot }(c) := K = \mathsf {H}(m',c)\). -
If \({\textsc {Decaps}}^{\bot }\) is queried on c first, no entry of the form (c, K) exists in \(\mathfrak {L}_{D}\) yet. Therefore, \({\textsc {Decaps}}^{\bot }\) adds
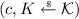 to \(\mathfrak {L}_{D}\), thereby defining \({\textsc {Decaps}}^{\bot }(c) := K.\) When queried on \((m',c)\) afterwards, \(\mathsf {H}\) recognizes that \({\mathsf {Dec}}_1( sk ,c)=m'\) in line 15 and that an entry of the form (c, K) already exists in \(\mathfrak {L}_{D}\) in line 19. By adding (m, c, K) to \(\mathfrak {L}_{H}\) and returning K, \(\mathsf {H}\) defines \(\mathsf {H}(m',c) := K = {\textsc {Decaps}}^{\bot }(c).\)
to \(\mathfrak {L}_{D}\), thereby defining \({\textsc {Decaps}}^{\bot }(c) := K.\) When queried on \((m',c)\) afterwards, \(\mathsf {H}\) recognizes that \({\mathsf {Dec}}_1( sk ,c)=m'\) in line 15 and that an entry of the form (c, K) already exists in \(\mathfrak {L}_{D}\) in line 19. By adding (m, c, K) to \(\mathfrak {L}_{H}\) and returning K, \(\mathsf {H}\) defines \(\mathsf {H}(m',c) := K = {\textsc {Decaps}}^{\bot }(c).\)
-
We have shown that \(\mathsf {B}\)’s view is identical in both games and
Game \(G_2\). From game \(G_2\) on we proceed identical to the proof of Theorem 4. That is, we abort immediately on the event that \(\mathsf {B}\) queries \(\mathsf {H}\) on \((m^*, c^*)\). Denote this event as \(\textsc {CHAL}\). Due to the difference lemma,
In game \(G_2\), \(\mathsf {H}(m^*, c^*)\) will not be given to \(\mathsf {B}\); neither through a hash nor a decryption query, meaning bit b is independent from \(\mathsf {B}\)’s view. Hence,
It remains to bound \(\Pr [\textsc {CHAL}]\). To this end, we construct an adversary \(\mathsf {A}\) against the \(\mathsf {OW}\text {-}\mathsf {PCVA}\) security of \({\mathsf {PKE}}_1\) simulating \(G_2\) for \(\mathsf {B}\) as in Fig. 11. Note that the simulation is perfect. Since \(\textsc {CHAL}\) implies that \(\mathsf {B}\) queried \(\mathsf {H}(m^*,c^*)\) which implies \((m^*, c^*, K') \in ~\mathfrak {L}_{H}\) for some \(K'\), and \(\mathsf {A}\) returns \(m'=m^*\). Hence,
Collecting the probabilities yields the required bound.
Transformation \({\mathbf {\mathsf{{U}}}}^{{\not \bot }}\) : From OW-PCA to IND-CCA. \({\mathsf {U}}^{{\not \bot }}\) is a variant of \({\mathsf {U}}^\bot \) with “implicit rejection” of inconsistent ciphertexts. It transforms an \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure public-key encryption scheme into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key encapsulation mechanism.
The Construction. To a public-key encryption scheme \({\mathsf {PKE}}_1= ({\mathsf {Gen}}_1, \mathsf {Enc}_1, {\mathsf {Dec}}_1)\) with message space \(\mathcal {M}\), and a random oracle \(\mathsf {H}: \{0,1\}^* \rightarrow \mathcal {M}\) we associate \({\mathsf {KEM}}^{\not \bot }= {\mathsf {U}}^{{\not \bot }}[{\mathsf {PKE}}_1,\mathsf {H}]=({\mathsf {Gen}}^{\not \bot },\mathsf {Encaps},{\mathsf {Decaps}}^{\not \bot })\). The algorithms of \({\mathsf {KEM}}^{\not \bot }\) are defined in Fig. 12, \(\mathsf {Encaps}\) is the same as in \({\mathsf {KEM}}^{\bot }\) (Fig. 9). Note that \({\mathsf {U}}^\bot \) and \({\mathsf {U}}^{{\not \bot }}\) essentially differ in decapsulation: \({\mathsf {Decaps}}^{\bot }\) from \({\mathsf {U}}^\bot \) rejects if c decrypts to \(\bot \), whereas \({\mathsf {Decaps}}^{\not \bot }\) from \({\mathsf {U}}^{{\not \bot }}\) returns a pseudorandom key K.
Security. The following theorem establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\not \bot }\) tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\), in the random oracle model.
Theorem 4
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then \({\mathsf {KEM}}^{\not \bot }\) is \(\delta _1\)-correct in the random oracle model. For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\not \bot }\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{{\not \bot }}\) and at most \(q_{\mathsf {H}}\) queries to the random oracle \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_{\mathsf {H}}\) queries to the \(\textsc {Pco}\) oracle such that
). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then \({\mathsf {KEM}}^{\not \bot }\) is \(\delta _1\)-correct in the random oracle model. For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\not \bot }\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{{\not \bot }}\) and at most \(q_{\mathsf {H}}\) queries to the random oracle \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_{\mathsf {H}}\) queries to the \(\textsc {Pco}\) oracle such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
The proof is very similar to the one of Theorem 3. The only difference is the handling of decapsulation queries with inconsistent ciphertexts. Hence, we defer the proof to the full version [26].
Transformations \({\mathbf {\mathsf{{U}}}}^{\varvec{{\not \bot }}_{\varvec{\textit{m}}}}\) / \({\mathbf {\mathsf{{U}}}}^{\varvec{\bot }_{\varvec{\textit{m}}}}\) : From OW-CPA / OW-VA to IND-CCA for deterministic Encryption. Transformation \({\mathsf {U}}^{\bot }_{\textit{m}}\) is a variant of \({\mathsf {U}}^\bot \) that derives the KEM key as \(K=\mathsf {H}(m)\), instead of \(K=\mathsf {H}(m,c)\). It transforms a \(\mathsf {OW}\text {-}\mathsf {VA}\) secure public-key encryption scheme with deterministic encryption (e.g., the ones obtained via \(\mathsf {T}\) from Sect. 3.1) into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key encapsulation mechanism. We also consider an implicit rejection variant \({\mathsf {U}}^{\not \bot }_\textit{m}\) that only requires \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of the underlying encryption scheme \(\mathsf {PKE}\).
The Construction. To a public-key encryption scheme \({\mathsf {PKE}}_1= ({\mathsf {Gen}}_1, \mathsf {Enc}_1, {\mathsf {Dec}}_1)\) with message space \(\mathcal {M}\), and a random oracle \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\), we associate \({\mathsf {KEM}}^{\not \bot }_\textit{m}= {\mathsf {U}}^{\not \bot }_\textit{m}[{\mathsf {PKE}}_1,\mathsf {H}]=({\mathsf {Gen}}^{\not \bot },\mathsf {Encaps}_\textit{m},{\mathsf {Decaps}}^{\not \bot }_\textit{m})\) and \({\mathsf {KEM}}^{\bot }_\textit{m}= {\mathsf {U}}^{\bot }_{\textit{m}}[{\mathsf {PKE}}_1,\mathsf {H}]=({\mathsf {Gen}}_1,\mathsf {Encaps}_\textit{m},\mathsf {Decaps}^{\bot }_\textit{m})\). Algorithm \({\mathsf {Gen}}^{\not \bot }\) is given in Fig. 12 and the remaining algorithms of \({\mathsf {KEM}}^{\not \bot }_\textit{m}\) and \({\mathsf {KEM}}^{\bot }_\textit{m}\) are defined in Fig. 13.
Security of \({\mathsf {KEM}}^{\bot }_\textit{m}\). The following theorem establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\bot }_\textit{m}\) tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {VA}\) security of \({\mathsf {PKE}}_1\), in the random oracle model. Again, the proof is similar to the one of Theorem 3 and can be found in [26].
Theorem 5
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then so is \({\mathsf {KEM}}^{\bot }_\textit{m}\). Let \(\mathsf {G}\) denote the random oracle that \({\mathsf {PKE}}_1\) uses (if any), and let \(q_{\mathsf {Enc}_1,\mathsf {G}}\) and \(q_{{\mathsf {Dec}}_1,\mathsf {G}}\) denote an upper bound on the number of \(\mathsf {G}\)-queries that \(\mathsf {Enc}_1\), resp. \({\mathsf {Dec}}_1\) makes upon a single invocation. If \(\mathsf {Enc}_1\) is deterministic then, for any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\bot }_\textit{m}\), issuing at most \(q_D\) queries to the decapsulation oracle \(\textsc {Decaps}^{\bot }_\textit{m}\) and at most \(q_{\mathsf {G}}\), resp. \(q_{\mathsf {H}}\) queries to its random oracles \(\mathsf {G}\) and \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {VA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_D\) queries to the \(\textsc {Cvo}\) oracle such that
). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then so is \({\mathsf {KEM}}^{\bot }_\textit{m}\). Let \(\mathsf {G}\) denote the random oracle that \({\mathsf {PKE}}_1\) uses (if any), and let \(q_{\mathsf {Enc}_1,\mathsf {G}}\) and \(q_{{\mathsf {Dec}}_1,\mathsf {G}}\) denote an upper bound on the number of \(\mathsf {G}\)-queries that \(\mathsf {Enc}_1\), resp. \({\mathsf {Dec}}_1\) makes upon a single invocation. If \(\mathsf {Enc}_1\) is deterministic then, for any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\bot }_\textit{m}\), issuing at most \(q_D\) queries to the decapsulation oracle \(\textsc {Decaps}^{\bot }_\textit{m}\) and at most \(q_{\mathsf {G}}\), resp. \(q_{\mathsf {H}}\) queries to its random oracles \(\mathsf {G}\) and \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {VA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) that makes at most \(q_D\) queries to the \(\textsc {Cvo}\) oracle such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
Security of \({\mathsf {KEM}}^{\not \bot }_\textit{m}\). The following theorem establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {KEM}}^{\not \bot }_\textit{m}\) tightly reduces to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \({\mathsf {PKE}}_1\), in the random oracle model. Its proof is easily obtained by combining the proofs of Theorems 4 and 5.
Theorem 6
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then so is \({\mathsf {KEM}}^{\not \bot }_\textit{m}\). Let \(\mathsf {G}\) denote the random oracle that \({\mathsf {PKE}}_1\) uses (if any), and let \(q_{\mathsf {Enc}_1,\mathsf {G}}\) and \(q_{{\mathsf {Dec}}_1,\mathsf {G}}\) denote an upper bound on the number of \(\mathsf {G}\)-queries that \(\mathsf {Enc}_1\), resp. \({\mathsf {Dec}}_1\) makes upon a single invocation. If \(\mathsf {Enc}_1\) is deterministic then, for any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\not \bot }_\textit{m}\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{{\not \bot }}_\textit{m}\) and at most \(q_{\mathsf {G}}\), resp. \(q_{\mathsf {H}}\) queries to its random oracles \(\mathsf {G}\) and \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) such that
). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, then so is \({\mathsf {KEM}}^{\not \bot }_\textit{m}\). Let \(\mathsf {G}\) denote the random oracle that \({\mathsf {PKE}}_1\) uses (if any), and let \(q_{\mathsf {Enc}_1,\mathsf {G}}\) and \(q_{{\mathsf {Dec}}_1,\mathsf {G}}\) denote an upper bound on the number of \(\mathsf {G}\)-queries that \(\mathsf {Enc}_1\), resp. \({\mathsf {Dec}}_1\) makes upon a single invocation. If \(\mathsf {Enc}_1\) is deterministic then, for any \(\mathsf {IND}\text {-}\mathsf {CCA}\) adversary \(\mathsf {B}\) against \({\mathsf {KEM}}^{\not \bot }_\textit{m}\), issuing at most \(q_D\) queries to the decapsulation oracle \({\textsc {Decaps}}^{{\not \bot }}_\textit{m}\) and at most \(q_{\mathsf {G}}\), resp. \(q_{\mathsf {H}}\) queries to its random oracles \(\mathsf {G}\) and \(\mathsf {H}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) against \({\mathsf {PKE}}_1\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
\(\mathsf {IND}\text {-}\mathsf {CCA}\) secure Key Encapsulation Mechanisms \({\mathsf {KEM}}^{\not \bot }=({\mathsf {Gen}}^{\not \bot },\mathsf {Encaps},{\mathsf {Decaps}}^{\not \bot })\), \({\mathsf {KEM}}^{\bot }=(\mathsf {Gen},\mathsf {Encaps},{\mathsf {Decaps}}^{\bot })\), \({\mathsf {KEM}}^{\not \bot }_\textit{m}=({\mathsf {Gen}}^{\not \bot },\mathsf {Encaps}_\textit{m},{\mathsf {Decaps}}^{\not \bot }_\textit{m})\), and \({\mathsf {KEM}}^{\bot }_\textit{m}=(\mathsf {Gen},\mathsf {Encaps}_\textit{m},\mathsf {Decaps}^{\bot }_\textit{m})\) obtained from \(\mathsf {PKE}=(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\).
3.3 The Resulting KEMs
For completeness, we combine transformation \(\mathsf {T}\) with \(\{{\mathsf {U}}^{{\not \bot }},{\mathsf {U}}^\bot ,{\mathsf {U}}^{\not \bot }_\textit{m}, {\mathsf {U}}^{\bot }_{\textit{m}}\}\) from the previous sections to obtain four variants of the FO transformation \(\mathsf {FO}:= {\mathsf {U}}^{{\not \bot }}\circ \mathsf {T}\), \({\mathsf {FO}}^\bot := {\mathsf {U}}^\bot \circ \mathsf {T}\), \({\mathsf {FO}}^{\not \bot }_\textit{m}:= {\mathsf {U}}^{\not \bot }_\textit{m}\circ \mathsf {T}\), and \({\mathsf {FO}}^\bot _\textit{m}:= {\mathsf {U}}^{\bot }_{\textit{m}}\circ \mathsf {T}\). To a public-key encryption scheme \(\mathsf {PKE}= (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) with message space \(\mathcal {M}\) and randomness space \(\mathcal {R}\), and hash functions \(\mathsf {G}: \mathcal {M}\rightarrow \mathcal {R}\), \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\) we associate
Their constituting algorithms are given in Fig. 14.
The following table provides (simplified) concrete bounds of the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \(\mathsf {KEM}\in \{{\mathsf {KEM}}^{\not \bot }, {\mathsf {KEM}}^{\bot },{\mathsf {KEM}}^{\not \bot }_\textit{m}, {\mathsf {KEM}}^{\bot }_\textit{m}\}\), directly obtained by combining Theorems 1−6. Here \(q_{\mathsf {RO}}:=q_\mathsf {G}+q_\mathsf {H}\) counts the total number of \(\mathsf {B}\)’s queries to the random oracles \(\mathsf {G}\) and \(\mathsf {H}\) and \(q_D\) counts the number of \(\mathsf {B}\)’s decryption queries. The left column provides the bounds relative to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) advantage, the right column relative to the \(\mathsf {IND}\text {-}\mathsf {CPA}\) advantage.

Concrete parameters. For “\(\kappa \) bits of security” one generally requires that for all adversaries \(\mathsf {B}\) with advantage \(\mathrm {Adv}(\mathsf {B})\) and running in time \(\mathrm {Time}(\mathsf {B})\), we have
The table below gives recommendations for the information-theoretic terms \(\delta \) (correctness error of \(\mathsf {PKE}\), \(\gamma \) (\(\gamma \)-spreadness of \(\mathsf {PKE}\)), and \(\mathcal {M}\) (message space of \(\mathsf {PKE}\)) appearing the concrete security bounds above.

For example, if the concrete security bound contains the term \(q_{\mathsf {RO}}\cdot \delta \), then with \(\delta \le 2^{-\kappa }\) one has
as required for \(\kappa \) bits security.
3.4 \({\mathsf {S}}^{\ell }\): From \(\mathsf {OW}\text {-}\mathsf {CPA}\) to \(\mathsf {IND}\text {-}\mathsf {CPA}\) Security, Tightly
\({\mathsf {S}}^{\ell }\) transforms an \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure public-key encryption scheme into an \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure scheme. The security reduction has a parameter \(\ell \) which allows for a tradeoff between the security loss of the reduction and the compactness of ciphertexts.
The Construction. Fix an \(\ell \in \mathbb {N}\). To a public-key encryption scheme \(\mathsf {PKE}= (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) with message space \(\mathcal {M}=\{0,1\}^n \) and a hash function \(\mathsf {F}: \mathcal {M}^\ell \rightarrow \mathcal {R}\), we associate \(\mathsf {PKE}_\ell = {\mathsf {S}}^{\ell }[\mathsf {PKE},\mathsf {F}]\). The algorithms of \(\mathsf {PKE}_\ell \) are defined in Fig. 15.
Security. The following theorem shows that \(\mathsf {PKE}_\ell \) is \(\mathsf {IND}\text {-}\mathsf {CPA}\) secure, provided that \(\mathsf {PKE}\) is \(\mathsf {OW}\text {-}\mathsf {CPA}\) secure. The proof (sketched in the introduction) is postponed to [26].
Theorem 7
(
 ). If \(\mathsf {PKE}\) is \(\delta \)-correct (in the ROM), then \(\mathsf {PKE}_\ell \) is \(\ell \cdot \delta \)-correct. Moreover, for any \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {F}}\) queries to random oracle \(\mathsf {F}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
). If \(\mathsf {PKE}\) is \(\delta \)-correct (in the ROM), then \(\mathsf {PKE}_\ell \) is \(\ell \cdot \delta \)-correct. Moreover, for any \(\mathsf {IND}\text {-}\mathsf {CPA}\) adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {F}}\) queries to random oracle \(\mathsf {F}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) adversary \(\mathsf {A}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
4 Modular FO Transformation in the QROM
In this section, we will revisit our transformations in the quantum random oracle model. In Sect. 4.1, we give a short primer on quantum computation and define the quantum random oracle model (QROM). In Sect. 4.2, we will state that transformation \(\mathsf {T}\) from Fig. 5 (Sect. 3.1) is also secure in the quantum random oracle model. Next, in Sect. 4.3 we will introduce \({\mathsf {QU}}^\bot _\textit{m}\) (\({\mathsf {QU}}^{\not \bot }_\textit{m}\)), a variant of \({\mathsf {U}}^{\bot }_{\textit{m}}\) (\({\mathsf {U}}^{\not \bot }_\textit{m}\)), which has provable security in the quantum random oracle model. Combining the two above transformations, in Sect. 4.4 we provide concrete bounds for the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {QKEM}}^\bot _\textit{m}={\mathsf {QFO}}^\bot _\textit{m}[\mathsf {PKE},\mathsf {G},\mathsf {H},\mathsf {H}']\) and \({\mathsf {QKEM}}^{\not \bot }_\textit{m}={\mathsf {QFO}}^{\not \bot }_\textit{m}[\mathsf {PKE},\mathsf {G},\mathsf {H},\mathsf {H}']\) in the QROM.
4.1 Quantum Computation
Qubits. For simplicity, we will treat a qubit as a vector \(|b \rangle \in \mathbb {C}^2\), i.e., a linear combination \(|b \rangle = \alpha \cdot |{0} \rangle + \beta \cdot |{1} \rangle \) of the two basis states (vectors) \(|{0} \rangle \) and \(|{1} \rangle \) with the additional requirement to the probability amplitudes \(\alpha , \beta \in \mathbb {C}\) that \(|\alpha |^2 + |\beta |^2 = 1.\) The basis \(\lbrace |{0} \rangle , |{1} \rangle \rbrace \) is called standard orthonormal computational basis. The qubit \(|b \rangle \) is said to be in superposition. Classical bits can be interpreted as quantum bits via the mapping \((b \mapsto 1 \cdot |{b} \rangle + 0 \cdot |{1-b} \rangle )\).
Quantum Registers. We will treat a quantum register as a collection of multiple qubits, i.e. a linear combination \(\sum _{(b_1, \cdots , b_n) \in \{0,1\}^n}^{} \alpha _{b_1 \cdots b_n} \cdot |{b_1 \cdots b_n} \rangle \), where \(\alpha _{b_1, \cdots , b_n} \in \mathbb {C}^n,\) with the additional restriction that \(\sum _{(b_1, \cdots , b_n) \in \{0,1\}^n}^{} |\alpha _{b_1 \cdots b_n}|^2 = 1.\) As in the one-dimensional case, we call the basis \(\lbrace |{b_1 \cdots b_n} \rangle \rbrace _{(b_1, \cdots , b_n) \in \{0,1\}^n}\) the standard orthonormal computational basis.
Measurements. Qubits can be measured with respect to a basis. In this paper, we will only consider measurements in the standard orthonormal computational basis, and denote this measurement by \(\textsc {Measure}(\cdot )\), where the outcome of \(\textsc {Measure}(|{b} \rangle )\) is a single qubit \(|b \rangle = \alpha \cdot |{0} \rangle + \beta \cdot |{1} \rangle \) will be \(|{0} \rangle \) with probability \(|\alpha |^2\) and \(|{1} \rangle \) with probability \(|\beta |^2\), and the outcome of measuring a qubit register \(\sum \limits _{b_1, \cdots , b_n \in \{0,1\}}^{} \alpha _{b_1 \cdots b_n} \cdot |{b_1 \cdots b_n} \rangle \) will be \(|{b_1 \cdots b_n} \rangle \) with probability \(|\alpha _{b_1 \cdots b_n}|^2\). Note that the amplitudes collapse during a measurement, this means that by measuring \(\alpha \cdot |{0} \rangle + \beta \cdot |{1} \rangle \), \(\alpha \) and \(\beta \) are switched to one of the combinations in \(\lbrace \pm (1,0),\ \pm (0,1)\rbrace .\) Likewise, in the n-dimensional case, all amplitudes are switched to 0 except for the one that belongs to the measurement outcome and which will be switched to 1.
Quantum oracles and quantum Adversaries. Following [5, 11], we view a quantum oracle as a mapping
where \(\textsc {O}: \{0,1\}^n \rightarrow \{0,1\}^{m}\), \(x \in \{0,1\}^n\) and \(y \in \{0,1\}^{m}\), and model quantum adversaries \(\mathsf {A}\) with access to \(\textsc {O}\) by the sequence \(U \circ \textsc {O}\), where U is a unitary operation. We write \(\mathsf {A}^{|{\textsc {O}} \rangle }\) to indicate that the oracles are quantum-accessible (contrary to oracles which can only process classical bits).
Quantum random oracle model. We consider security games in the quantum random oracle model (QROM) as their counterparts in the classical random oracle model, with the difference that we consider quantum adversaries that are given quantum access to the random oracles involved, and classical access to all other oracles (e.g., plaintext checking or decapsulation oracles). Zhandry [41] proved that no quantum algorithm \(\mathsf {A}^{|{f} \rangle }\), issuing at most q quantum queries to \(|{f} \rangle \), can distinguish between a random function \(f :\{0,1\}^m \rightarrow \{0,1\}^n\) and a 2q-wise independent function. It allows us to view quantum random oracles as polynomials of sufficient large degree. That is, we define a quantum random oracle \(| \mathsf {H}\rangle \) as an oracle evaluating a random polynomial of degree 2q over the finite field \(\mathbb {F}_{2^n}\).
Correctness of \(\mathsf {PKE}\) in the QROM. Similar to the classical random oracle model, we need to define correctness of encryption in the quantum random oracle model. If \(\mathsf {PKE}= \mathsf {PKE}^\mathsf {G}\) is defined relative to a random oracle \({|\mathsf {G}\rangle }\), then again the correctness bound might depend on the number of queries to \({|\mathsf {G}\rangle }\). We call a public-key encryption scheme \(\mathsf {PKE}\) in the quantum random oracle model \(\delta (q_\mathsf {G})\)-correct if for all (possibly unbounded, quantum) adversaries \(\mathsf {A}\) making at most \(q_\mathsf {G}\) queries to quantum random oracle \({|\mathsf {G}\rangle }\), \(\Pr [\mathsf {COR}\text {-}\mathsf {QRO}^\mathsf {A}_\mathsf {PKE}\Rightarrow 1] \le \delta (q_\mathsf {G})\), where the correctness game \(\mathsf {COR}\text {-}\mathsf {QRO}\) is defined as in Fig. 16.
4.2 Transformation \(\mathsf {T}\): From \(\mathsf {OW}\text {-}\mathsf {CPA}\) to \(\mathsf {OW}\text {-}\mathsf {PCA}\) in the QROM
Recall transformation \(\mathsf {T}\) from Fig. 5 of Sect. 3.1.
Lemma 2
Assume \(\mathsf {PKE}\) to be \(\delta \)-correct. Then \({\mathsf {PKE}}_1=\mathsf {T}[\mathsf {PKE},\mathsf {G}]\) is \(\delta _1\)-correct in the quantum random oracle model, where \(\delta _1=\delta _1(q_\mathsf {G}) \le 8 \cdot (q_{\mathsf {G}} + 1 )^2 \cdot \delta \).
It can be shown that \(\delta _1(q_\mathsf {G})\) can be upper bounded by the success probability of an (unbounded, quantum) adversary against a generic search problem. For more details, refer to the full version [26].
The following theorem (whose proof is loosely based on [38]) establishes that \(\mathsf {IND}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\) reduces to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of \(\mathsf {PKE}\), in the quantum random oracle model.
Theorem 8
(
 ). Assume \(\mathsf {PKE}\) to be \(\delta \)-correct. For any \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the quantum random oracle \(|\mathsf {G}\rangle \) and \(q_P\) (classical) queries to the plaintext checking oracle \(\textsc {Pco}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) quantum adversary \(\mathsf {A}\) such that
). Assume \(\mathsf {PKE}\) to be \(\delta \)-correct. For any \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {B}\) that issues at most \(q_{\mathsf {G}}\) queries to the quantum random oracle \(|\mathsf {G}\rangle \) and \(q_P\) (classical) queries to the plaintext checking oracle \(\textsc {Pco}\), there exists an \(\mathsf {OW}\text {-}\mathsf {CPA}\) quantum adversary \(\mathsf {A}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
Similar to the proof of Theorem 1, the proof first implements the \(\mathsf {PCA}\) oracle via “re-encryption”. Next, we apply an algorithmic adaption of OW2H from [39] to decouple the challenge ciphertext \(c^*:=\mathsf {Enc}( pk ,m^*; \mathsf {G}(m^*))\) from the random oracle \(\mathsf {G}\). The decoupling allows for a reduction from \(\mathsf {OW}\text {-}\mathsf {CPA}\) security. Again, we defer to [26] for details.
4.3 Transformations \({\mathsf {QU}}^\bot _\textit{m}\), \({\mathsf {QU}}^{\not \bot }_\textit{m}\)
Transformation \({\mathbf {\mathsf{{QU}}}}^{\varvec{\bot }}_{\varvec{\textit{m}}}\) : From OW-PCA to IND-CCA in the QROM. \({\mathsf {QU}}^\bot _\textit{m}\) transforms an \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure public-key encryption scheme into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key encapsulation mechanism with explicit rejection.
The Construction. To a public-key encryption scheme \({\mathsf {PKE}}_1= ({\mathsf {Gen}}_1, \mathsf {Enc}_1, {\mathsf {Dec}}_1)\) with message space \(\mathcal {M}= \{0,1\}^{n}\), and hash functions \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\) and \(\mathsf {H}': \{0,1\}^n \rightarrow \{0,1\}^n\), we associate \({\mathsf {QKEM}}^\bot _\textit{m}= {\mathsf {QU}}^\bot _\textit{m}[{\mathsf {PKE}}_1,\mathsf {H},\mathsf {H}']\). The algorithms of \({\mathsf {QKEM}}^\bot _\textit{m}= (\mathsf {QGen}:={\mathsf {Gen}}_1,\mathsf {QEncaps}_\textit{m},{\mathsf {QDecaps}}^\bot _\textit{m})\) are defined in Fig. 17. We stress that hash function \(\mathsf {H}'\) has matching domain and range.
Security. The following theorem (whose proof is again loosely based on [38] and is postponed to [26]) establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {QKEM}}^\bot _\textit{m}\) reduces to the \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\), in the quantum random oracle model.
Theorem 9
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, so is \({\mathsf {QKEM}}^\bot _\textit{m}\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) quantum adversary \(\mathsf {B}\) issuing at most \(q_D\) (classical) queries to the decapsulation oracle \({\textsc {QDecaps}}^\bot _\textit{m}\), at most \(q_{\mathsf {H}}\) queries to the quantum random oracle \(|\mathsf {H}\rangle \) and at most \(q_{\mathsf {H}'}\) queries to the quantum random oracle \(|\mathsf {H}' \rangle \), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {A}\) issuing \(2 q_D q_{\mathsf {H}'} \) queries to oracle \(\textsc {Pco}\) such that
). If \({\mathsf {PKE}}_1\) is \(\delta _1\)-correct, so is \({\mathsf {QKEM}}^\bot _\textit{m}\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) quantum adversary \(\mathsf {B}\) issuing at most \(q_D\) (classical) queries to the decapsulation oracle \({\textsc {QDecaps}}^\bot _\textit{m}\), at most \(q_{\mathsf {H}}\) queries to the quantum random oracle \(|\mathsf {H}\rangle \) and at most \(q_{\mathsf {H}'}\) queries to the quantum random oracle \(|\mathsf {H}' \rangle \), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {A}\) issuing \(2 q_D q_{\mathsf {H}'} \) queries to oracle \(\textsc {Pco}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
Transformation \({\mathbf {\mathsf{{QU}}}}^{\varvec{{\not \bot }}_{\varvec{\textit{m}}}}\) : From OW-PCA to IND-CCA in the QROM. \({\mathsf {QU}}^{\not \bot }_\textit{m}\) transforms an \(\mathsf {OW}\text {-}\mathsf {PCA}\) secure public-key encryption scheme into an \(\mathsf {IND}\text {-}\mathsf {CCA}\) secure key encapsulation mechanism with implicit rejection.
The Construction. To a public-key encryption scheme \({\mathsf {PKE}}_1= ({\mathsf {Gen}}_1, \mathsf {Enc}_1, {\mathsf {Dec}}_1)\) with message space \(\mathcal {M}= \{0,1\}^{n}\), and hash functions \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\) and \(\mathsf {H}': \{0,1\}^n \rightarrow \{0,1\}^n\), we associate \({\mathsf {QKEM}}^{\not \bot }_\textit{m}= {\mathsf {QU}}^{\not \bot }_\textit{m}[{\mathsf {PKE}}_1,\mathsf {H},\mathsf {H}']= (\mathsf {QGen}:={\mathsf {Gen}}^{\not \bot },\mathsf {QEncaps}_\textit{m},{\mathsf {QDecaps}}^{\not \bot }_\textit{m})\). Algorithm \({\mathsf {Gen}}^{\not \bot }\) is given in Fig. 12 and the remaining algorithms of \({\mathsf {QKEM}}^{\not \bot }_\textit{m}\) are defined in Fig. 18. We stress again that hash function \(\mathsf {H}'\) has matching domain and range.
Security. The following theorem (whose proof is deferred to [26]) establishes that \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \({\mathsf {QKEM}}^{\not \bot }_\textit{m}\) reduces to the \(\mathsf {OW}\text {-}\mathsf {PCA}\) security of \({\mathsf {PKE}}_1\), in the quantum random oracle model.
Theorem 10
(
 ). If \({\mathsf {PKE}}_1\) is \(\delta \)-correct, so is \({\mathsf {QKEM}}^{\not \bot }_\textit{m}\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) quantum adversary \(\mathsf {B}\) issuing at most \(q_D\) (classical) queries to the decapsulation oracle \({\textsc {QDecaps}}^{\not \bot }_\textit{m}\), at most \(q_{\mathsf {H}}\) queries to the quantum random oracle \(|\mathsf {H}\rangle \) and at most \(q_{\mathsf {H}'}\) queries to the quantum random oracle \(|\mathsf {H}' \rangle \), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {A}\) issuing \(2 q_D q_{\mathsf {H}'} \) queries to oracle \(\textsc {Pco}\) such that
). If \({\mathsf {PKE}}_1\) is \(\delta \)-correct, so is \({\mathsf {QKEM}}^{\not \bot }_\textit{m}\). For any \(\mathsf {IND}\text {-}\mathsf {CCA}\) quantum adversary \(\mathsf {B}\) issuing at most \(q_D\) (classical) queries to the decapsulation oracle \({\textsc {QDecaps}}^{\not \bot }_\textit{m}\), at most \(q_{\mathsf {H}}\) queries to the quantum random oracle \(|\mathsf {H}\rangle \) and at most \(q_{\mathsf {H}'}\) queries to the quantum random oracle \(|\mathsf {H}' \rangle \), there exists an \(\mathsf {OW}\text {-}\mathsf {PCA}\) quantum adversary \(\mathsf {A}\) issuing \(2 q_D q_{\mathsf {H}'} \) queries to oracle \(\textsc {Pco}\) such that
and the running time of \(\mathsf {A}\) is about that of \(\mathsf {B}\).
4.4 The Resulting KEMs
For concreteness, we combine transformations \(\mathsf {T}\) and \(\{{\mathsf {QU}}^\bot _\textit{m}, {\mathsf {QU}}^{\not \bot }_\textit{m}\}\) from the previous sections to obtain \({\mathsf {QFO}}^\bot _\textit{m}= \mathsf {T}\circ {\mathsf {QU}}^\bot _\textit{m}\) and \({\mathsf {QFO}}^{\not \bot }_\textit{m}= \mathsf {T}\circ {\mathsf {QU}}^{\not \bot }_\textit{m}\). To a public-key encryption scheme \(\mathsf {PKE}= (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) with message space \(\mathcal {M}= \{0,1\}^{n}\) and randomness space \(\mathcal {R}\), and hash functions \(\mathsf {G}: \mathcal {M}\rightarrow \mathcal {R}\), \(\mathsf {H}: \{0,1\}^* \rightarrow \{0,1\}^n\) and \(\mathsf {H}': \{0,1\}^n \rightarrow \{0,1\}^n\), we associate
Algorithm \({\mathsf {Gen}}^{\not \bot }\) is given in Fig. 12 and the remaining algorithms are given in Fig. 19.
The following table provides (simplified) concrete bounds of the \(\mathsf {IND}\text {-}\mathsf {CCA}\) security of \(\mathsf {KEM}\in \{{\mathsf {QKEM}}^{\not \bot }_\textit{m}, {\mathsf {QKEM}}^\bot _\textit{m}\}\) in the quantum random oracle model, directly obtained by combining Theorems 8−10. Here \(q_{\mathsf {RO}}:=q_\mathsf {G}+ q_\mathsf {H}+ q_\mathsf {H}'\) counts the total number of (implicit and explicit) queries to the quantum random oracles \(\mathsf {G}\), \(\mathsf {H}\) and \(\mathsf {H}'\).

Notes
- 1.
Lattice-based encryption schemes can be made perfectly correctness by putting a limit on the noise and setting the modulus of the LWE instance large enough, see e.g. [9, 27]. But increasing the size of the modulus makes the LWE problem easier to solve in practice, and thus the dimension of the problem needs to be increased in order to obtain the same security levels. Larger dimension and modulus increase the public-key and ciphertext length.
- 2.
\(\mathsf {OW}\text {-}\mathsf {PCVA}\) security is called \(\mathsf {OW}\text {-}\mathsf {CPA}^+\) security with access to a \(\textsc {Pco}\) oracle in [20].
- 3.
\(\mathsf {OW}\text {-}\mathsf {VA}\) security is \(\mathsf {OW}\text {-}\mathsf {CPA}\) security, where the adversary is given access to a validity oracle \(\textsc {Cvo}(c)\) that checks c’s validity (cf. Definition 1).
- 4.
For an example why the number of random oracle queries matters in the context of correctness, we refer to Theorem 1.
References
Abdalla, M., Bellare, M., Rogaway, P.: The oracle Diffie-Hellman assumptions and an analysis of DHIES. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 143–158. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45353-9_12
Albrecht, M.R., Orsini, E., Paterson, K.G., Peer, G., Smart, N.P.: Tightly secure Ring-LWE based key encapsulation with short ciphertexts. Cryptology ePrint Archive, Report 2017/354 (2017). http://eprint.iacr.org/2017/354
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange - a new hope. In: 25th USENIX Security Symposium, USENIX Security 2016, Austin, TX, USA, pp. 327–343, 10–12 August 2016
Baek, J., Lee, B., Kim, K.: Secure length-saving ElGamal encryption under the computational Diffie-Hellman assumption. In: Dawson, E.P., Clark, A., Boyd, C. (eds.) ACISP 2000. LNCS, vol. 1841, pp. 49–58. Springer, Heidelberg (2000). https://doi.org/10.1007/10718964_5
Beals, R., Buhrman, H., Cleve, R., Mosca, M., Wolf, R.: Quantum lower bounds by polynomials. In: 39th FOCS, pp. 352–361. IEEE Computer Society Press, November 1998
Bellare, M., Boldyreva, A., O’Neill, A.: Deterministic and efficiently searchable encryption. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 535–552. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_30
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Bernstein, D.J., Chuengsatiansup, C., Lange, T., van Vredendaal, C.: NTRU prime. Cryptology ePrint Archive, Report 2016/461 (2016). http://eprint.iacr.org/2016/461
Bitansky, N., Vaikuntanathan, V.: A note on perfect correctness by derandomization. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 592–606. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_20
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Bos, J., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V., Schanck, J.M., Schwabe, P., Stehlé, D.: Crystals - Kyber: a CCA-secure module-lattice-based KEM. Cryptology ePrint Archive, Report 2017/634 (2017). http://eprint.iacr.org/2017/634
Bos, J.W., Costello, C., Ducas, L., Mironov, I., Naehrig, M., Nikolaenko, V., Raghunathan, A., Stebila, D.: Frodo: take off the ring! Practical, quantum-secure key exchange from LWE. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 1006–1018. ACM Press, October 2016
Bos, J.W., Costello, C., Naehrig, M., Stebila, D.: Post-quantum key exchange for the TLS protocol from the ring learning with errors problem. In: 2015 IEEE Symposium on Security and Privacy, pp. 553–570. IEEE Computer Society Press, May 2015
Cash, D., Kiltz, E., Shoup, V.: The twin Diffie-Hellman problem and applications. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 127–145. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_8
Cash, D., Kiltz, E., Shoup, V.: The twin Diffie-Hellman problem and applications. J. Cryptol. 22(4), 470–504 (2009)
Cheon, J.H., Kim, D., Lee, J., Song, Y.: Lizard: Cut off the tail! Practical post-quantum public-key encryption from LWE and LWR. Cryptology ePrint Archive, Report 2016/1126 (2016). http://eprint.iacr.org/2016/1126
Coron, J.S., Handschuh, H., Joye, M., Paillier, P., Pointcheval, D., Tymen, C.: GEM: a generic chosen-ciphertext secure encryption method. In: Preneel, B. (ed.) CT-RSA 2002. LNCS, vol. 2271, pp. 263–276. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45760-7_18
Cramer, R., Shoup, V.: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. SIAM J. Comput. 33(1), 167–226 (2003)
Dent, A.W.: A designer’s guide to KEMs. In: Paterson, K.G. (ed.) Cryptography and Coding 2003. LNCS, vol. 2898, pp. 133–151. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-40974-8_12
Ding, J., Xie, X., Lin, X.: A simple provably secure key exchange scheme based on the learning with errors problem. Cryptology ePrint Archive, Report 2012/688 (2012). http://eprint.iacr.org/2012/688
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_21
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 537–554. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_34
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Galindo, D., Martín, S., Morillo, P., Villar, J.L.: Fujisaki-Okamoto hybrid encryption revisited. Int. J. Inf. Secur. 4(4), 228–241 (2005)
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. Cryptology ePrint Archive, Report 2017/604 (2017). https://eprint.iacr.org/2017/604
Howgrave-Graham, N., Silverman, J.H., Whyte, W.: Choosing parameter sets for NTRUEncrypt with NAEP and SVES-3. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 118–135. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_10
Kiltz, E., Malone-Lee, J.: A general construction of IND-CCA2 secure public key encryption. In: Paterson, K.G. (ed.) Cryptography and Coding 2003. LNCS, vol. 2898, pp. 152–166. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-40974-8_13
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Lyubashevsky, V., Peikert, C., Regev, O.: A toolkit for Ring-LWE cryptography. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 35–54. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_3
NIST: National institute for standards and technology. Postquantum crypto project (2017). http://csrc.nist.gov/groups/ST/post-quantum-crypto
Okamoto, T., Pointcheval, D.: REACT: rapid enhanced-security asymmetric cryptosystem transform. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 159–174. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45353-9_13
Peikert, C.: Lattice cryptography for the internet. Cryptology ePrint Archive, Report 2014/070 (2014). http://eprint.iacr.org/2014/070
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_35
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Shoup, V.: ISO 18033–2: An emerging standard for public-key encryption, December 2004. http://shoup.net/iso/std6.pdf. Final Committee Draft
Shoup, V.: Sequences of games: a tool for taming complexity in security proofs. Cryptology ePrint Archive, Report 2004/332 (2004). http://eprint.iacr.org/2004/332
Targhi, E.E., Unruh, D.: Post-quantum security of the Fujisaki-Okamoto and OAEP transforms. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 192–216. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_8
Unruh, D.: Revocable quantum timed-release encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 129–146. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_8
Unruh, D.: Non-interactive zero-knowledge proofs in the quantum random oracle model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 755–784. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_25
Zhandry, M.: Secure identity-based encryption in the quantum random oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Acknowledgments
We would like to thank Andreas Hülsing, Christian Schaffner, and Dominique Unruh for interesting discussions on the FO transformation in the QROM. We are also grateful to Krzysztof Pietrzak and Victor Shoup for discussions on Sect. 3.4. The first author was supported in part by ERC project PREP-CRYPTO (FP7/724307) and by DFG grants HO4534/4-1 and HO4534/2-2. The second author was supported by DFG RTG 1817/1 UbiCrypt. The third author was supported in part by ERC Project ERCC (FP7/615074) and by DFG SPP 1736 Big Data.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Hofheinz, D., Hövelmanns, K., Kiltz, E. (2017). A Modular Analysis of the Fujisaki-Okamoto Transformation. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)















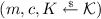 to
to 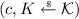 to
to 








