Labeled Homomorphic Encryption

Abstract

In privacy-preserving processing of outsourced data a Cloud server stores data provided by one or multiple data providers and then is asked to compute several functions over it. We propose an efficient methodology that solves this problem with the guarantee that a honest-but-curious Cloud learns no information about the data and the receiver learns nothing more than the results. Our main contribution is the proposal and efficient instantiation of a new cryptographic primitive called Labeled Homomorphic Encryption (labHE). The fundamental insight underlying this new primitive is that homomorphic computation can be significantly accelerated whenever the program that is being computed over the encrypted data is known to the decrypter and is not secret—previous approaches to homomorphic encryption do not allow for such a trade-off. Our realization and implementation of labHE targets computations that can be described by degree-two multivariate polynomials. As an application, we consider privacy preserving Genetic Association Studies (GAS), which require computing risk estimates from features in the human genome. Our approach allows performing GAS efficiently, non interactively and without compromising neither the privacy of patients nor potential intellectual property of test laboratories.

1 Introduction

Privacy-preserving data processing techniques are crucial enablers for moving many security-critical applications to the Cloud, and they may be the key to unlocking new socially-relevant applications and business opportunities. As an example, consider the case of personalized medicine, where a medical center offers highly specialized services that permit guiding the medical care of a Client based on information encoded in the Genome. Such direct-to-consumer services are already a reality, so we will not discuss whether or not they are desirable. Instead, we propose a new methodology that can be used today to deploy such services in the Cloud (genomic studies may involve a huge amount of data), whilst protecting the privacy of the Client, and intellectual property that may be a concern for the medical center. Controlling who has access to individual data in these scenarios will likely be mandatory for ethical and/or legal reasons, and this pattern arises in many other real-world applications (e.g., analysis of taxpayers’ or consumers’ data, users’ geographic locations, etc.) where our solution may be of use.

Fig. 1.

The parties and workflow of our system.

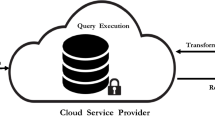
We consider a scenario with three actors – data providers, the Cloud, and a receiver – with the following workflow (Fig. 1). Data providers send data to the Cloud, and the receiver asks the Cloud to execute certain queries on the outsourced data. For the applications we consider, the key requirements are privacy and efficiency. Privacy properties should guarantee that the Cloud does not learn any information on the hosted data, and that the receiver learns nothing more than the queries outcomes. Furthermore, it should be possible for many data providers to contribute with inputs to the same computation, in such a way that data introduced by one provider is protected from the others. The efficiency requirement involves two main aspects: computation and communication. With respect to computation, the protocol should have minimal impact for data providers. There is little point for them in delegating storage and/or computation to the Cloud if this requires prohibitive costs; their only task should be to collect and send data and be minimally involved in the rest of the protocol (e.g., they could go offline). Moreover, in several applications the data providers can be resource-constrained devices (e.g., sensors) for which a lightweight protocol is essential. In terms of computation, the protocol should also run efficiently at the Cloud. Although Cloud providers have powerful resources, in an outsourcing setting one has to pay for them and thus the lighter is the protocol’s burden the cheaper is the service’s cost. On the communication side, one would like solutions with minimal bandwidth overhead both between data providers and the Cloud, and between the Cloud and the receiver. For example, the communication with the receiver should not depend on the amount of data hosted by the Cloud. Low bandwidth is particularly relevant in the context of mobile networks and mobile devices: high bandwidth consumptions drain batteries and cost a lot due to the price of mobile network connections (most of the times under a pay-per-use model).

Our Contribution.  We propose and efficiently instantiate a new cryptographic primitive called Labeled Homomorphic Encryption (labHE) that gives a solution to the problem of privately processing outsourced data outlined above. Our realization and implementation of labHE targets computations that can be described by degree-two multivariate polynomials, which capture a significant fraction of statistical functions and, in particular, statistical computations used in genomic analysis. As we detail later, our solution outperforms protocols based on previous somewhat homomorphic encryption schemes in essentially all fronts: our communication costs are more than two orders of magnitude smaller, computation is more than 80 times faster for data providers and up to 9000 times faster for the Cloud. The insight that unlocks such performance gains is that homomorphic computation can be significantly accelerated whenever the program that is being computed over the encrypted data is known to decrypter and is not secret—previous approaches to homomorphic encryption do not allow for such a trade-off.

Labeled Homomorphic Encryption.  Our new labHE notion combines the model of labeled programs, put forward in the context of homomorphic authenticators (e.g. [5, 7, 15]), with the concept of homomorphic encryption. Homomorphic encryption (HE) [16, 27] is like ordinary encryption with the additional capability of a (publicly executable) evaluation algorithm Eval. The latter takes as input a program P and encrypted messages $m_1, \ldots , m_n$, and outputs an encryption of $P(m_1, \ldots , m_n)$.

labHE is similar to HE with the following additions. First, every piece of (encrypted) data is associated with a unique label. A label could be the index of a database record or any other string that can be used to identify the outsourced data item. Thus, when encrypting a message m, one specifies a corresponding label $\tau$ (which does not need to be kept secret, though). To give an example, think of a blood pressure sensor which collects measurements at regular time instants: the pressure value is the actual data while the time instant is the label. Next, whenever a user Bob wants to ask the cloud to compute f on some (previously outsourced) encrypted inputs, he makes the query by specifying the labels of these inputs. For instance, Bob may say “compute the mean on messages with labels $({Pressure},1), \ldots , ({Pressure},100)$”. The combination of f and the labels in the query is called a “labeled program” P, which is what is executed by the Cloud. Finally, upon the receipt of the (encrypted) answer c from the Cloud, Bob runs the decryption algorithm with his secret key, c, and labeled program P. Introducing labeled programs in HE formalizes the intuition that Bob is decrypting the result of a known function (the labeled program, the query) on the unknown outsourced data (the encrypted messages). We stress that in the outsourcing setting labeling is always implicit, as some mechanism is always needed to specify the portion of the outsourced data over which the Cloud has to compute. Moreover, although one may wonder that labels leak additional information, it is not hard to see that this can be avoided by choosing an appropriate labeling (e.g., simple indices) which reveals only trivial information.

For efficiency we require labHE ciphertexts to be succinct, i.e., of fixed size, independent of the computation executed on it. We concede that the running time of labHE decryption may depend on P: this is the most noticeable difference with standard HE. Interestingly, however, in our realizations this has almost negligible impact on efficiency in practice. For security, we require labHE to meet the usual semantic security notion (i.e., one cannot tell apart encryptions of known messages) and also to satisfy a property that we call context-hiding. This essentially says that a ciphertext encrypting the result $m = P(m_1, \ldots , m_n)$ reveals only m and nothing more about the program inputs.

Basic and Multi-user labHE .  The basic labHE notion requires the same secret key to encrypt and decrypt. It can be used to perform privacy-preserving computations on outsourced data as follows. A data provider, Alice, jointly executes the setup algorithm with Bob, the receiver, and gets a secret encryption key that she can use to encrypt her data before outsourcing it to the Cloud. Bob can then ask the Cloud to compute a labeled program P on Alice’s data, obtain an encryption of the result and decrypt this with his secret decryption key. In terms of data privacy, labHE semantic security ensures that, as long as the Cloud does not get to see the keys used for encryption/decryption, it does not learn anything about Alice’s data or the result of the computation; context-hiding further guarantees that, as long as the Cloud does not reveal the originally encrypted ciphertexts to Bob, then Bob learns only the query results and no other information about Alice’s individual data. We note that this trust model is particularly well suited to a scenario in which Alice (or more of the senders in the multi-sender scenario below) controls the Cloud and uses it to offer a service to Bob. Regarding efficiency, the only work of Alice is to encrypt and transmit the data, while the succinctness of labHE yields short communication between the Cloud and Bob: answers received by Bob do not depend on the size of the outsourced data.

In addition to basic labHE, we also provide a more powerful generalization to a multi-user setting, which inherits all the performance features of the basic one. Here one can perform computations over data encrypted by different providers, and these do not need to share any common secret. Indeed, key generation in the basic labHE notion can be split between sender and receiver as follows. Bob generates a master public key and a master secret key. Knowing Bob’s master public key, Alice can unilaterally encrypt with her own generated encryption key, and create a public key that becomes associated with her encrypted data. In this way, no trusted a priori set-up is required in addition to a PKI. Moreover, multiple senders can do exactly the same as Alice to encrypt under their public keys and Bob’s master public key, with the extra guarantee that the data encrypted by one sender cannot be decrypted by a different sender. Decryption requires knowledge of the master secret along with the public keys of all the users whose ciphertexts were involved in the computation.

On the Usefulness of Labeling Programs.  The essence of labHE is to take advantage of the fact that, when delegating some computation P on outsourced data, P is typically provided explicitly to the cloud. Interestingly, when using (standard) homomorphic encryption this inherent privacy loss does not seem to be exploitable to gain efficiency. labHE, on the other hand, aims at trading the (unavoidable!) leak of P to significantly reduce the cost of the computation.

Indeed, the main difference with respect to (standard) homomorphic encryption is in decryption: decrypting in labHE requires Bob to do work that depends on the program P. More precisely, and simplifying things a bit, Bob will basically need to recompute P on (values related to) the labels corresponding to the original inputs. Interestingly we show that, as this computation is performed on unencrypted and very succinct data (short pseudorandom fingerprints of the labels), it has very low impact in practice. In fact, the cost of decryption is always orders of magnitude lower than that of running the computation in the Cloud. Not only that, this can be done prior to receiving the encrypted results from the Cloud! This becomes particularly interesting when considering that our realizations of labHE are extremely efficient also for the Cloud (see below for more details about this). Indeed, we show that, building on [6], $\mathsf{labHE}$ supporting computations expressible via degree-2 polynomials can be realized from any encryption scheme that is only linearly homomorphic. Since these are typically more efficient than their more expressive counterparts, the same holds for the resulting $\mathsf{labHE}$.

To the best of our knowledge, the idea of trading-off function privacy for efficiency has not been previously applied in the field of (somewhat) homomorphic encryption; for this reason, and while our work focuses on the specific case of computing degree two polynomials on ciphertexts, we believe that this idea could be of independent interest and might find applications for settings requiring more expressive computations as well.

An Overview of Our Techniques.  We provide an intuitive description of our solution, discussing some of the core ideas underlying it. We encrypt a message $m \in \mathcal{M}$ via a two-component ciphertext $(m-b, \mathsf{Enc}(b))$, where $\mathsf{Enc}$ is a linearly homomorphic encryption scheme and b is random in $\mathcal{M}$. In [6], Catalano and Fiore show that ciphertexts of this form allow for the evaluation of degree-two polynomials on encrypted data, at the cost of losing compactness. More precisely, Catalano and Fiore argue that when applying a polynomial f on $(m_1-b_1, \mathsf{Enc}(b_1)), \ldots , (m_{t}-b_{t}, \mathsf{Enc}(b_{t}))$, there may be the possibility (depending on the structure of f) to end up with a huge O(t)-components ciphertext $(\mathsf{Enc}(f(m_1, \ldots , m_t) - f(b_1, \ldots , b_{t})), \mathsf{Enc}(b_1), \ldots , \mathsf{Enc}(b_{t}))$.

Our key idea to solve the compactness issue in the context of labHE is to let every $b_i$ depend on the corresponding label; in our construction we set $b_i$ as the output of $F_K(\tau _i)$, where F is a pseudorandom function and $\tau _i$ is the unique label associated with message $m_i$. The crucial observation is that, because the labels are known to the decryptor, the value $f(b_1, \ldots , b_{t})$ can be reconstructed at decryption time, and the components $\mathsf{Enc}(b_1), \ldots , \mathsf{Enc}(b_t)$ dismissed from the above ciphertext. This gives us a construction that supports all degree-two polynomials with constant-size ciphertexts! Interestingly, this simple idea, when instantiated with fast cryptographic primitives (e.g., the Sponge-based pseudorandom function from the Kekkac Code Package and the Joye-Libert cryptosystem [20]) yields an extremely efficient realization of the primitive, that allows to outsource the computation of various useful functions (e.g. statistics, genetic association studies) in a very efficient yet privacy preserving way.

Efficient labHE Realizations.  We show how to construct expressive labHE schemes for quadratic functions by using standard number theoretic (linearly-homomorphic) encryption schemes, such as Paillier [25], Bresson et al. [4] and Joye-Libert [20]. We implemented one of these instantiations – the one based on the Joye-Libert cryptosystem that we call labHE(JL13) – and tested its performance for the case of computing statistical functions on encrypted data. Our experiments demonstrate that labHE(JL13) outperforms a solution based on state-of-the-art somewhat homomorphic encryption (FV) [13, 24] (optimized to support the same class of functions) on essentially all fronts. For example, comparing labHE(JL13) against FV, we observed that in labHE(JL13) the communication costs are 400 times smaller, encrypting is more than 80 times faster, while computing the results is between 9000 and 50 times faster for the Cloud.

Applications.  To further highlight the performance benefits of our solution in the real world, we looked at two specific applications: i. computing relevant statistical functions over encrypted data outsourced to the Cloud and ii. performing Genetic Association Studies that preserve both the privacy of users and the intellectual property of the laboratories performing the tests. These applications are discussed in Sect. 6.

Solutions Based on Related Primitives.  In the full version [1] we discuss how alternative solutions for the same applications could be developed using other cryptographic techniques—other forms of homomorphic encryption, secure multiparty computation and classical techniques—emphasizing the advantages of labelled homomorphic encryption in terms of computational costs and bandwidth in each chase, and highlighting the differences in trust models and necessary infrastructure.

Preliminaries and Notation.  We denote with $\lambda \in \mathbb N$ a security parameter, and with $\mathsf{poly}(\lambda )$ any function bounded by a polynomial in $\lambda$. We say that a function $\epsilon$ is negligible if it vanishes faster than the inverse of any polynomial in $\lambda$. We use PPT for probabilistic polynomial time, i.e., $\mathsf{poly}(\lambda )$. If S is a set, $x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S$ denotes selecting x uniformly at random in S. If $\mathcal{A}$ is a probabilistic algorithm, $x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{A}(\cdot )$ denotes the process of running $\mathcal{A}$ on some appropriate input and assigning its output to x. For a positive integer n, we denote by [n] the set $\{1, \ldots , n\}$. We refer to [16] for standard security notions related to HE.

2 Labeled HE

In this section we introduce the notion of Labeled Homomorphic Encryption (labHE, for short). This notion adapts the one of (symmetric-key) homomorphic encryption to the setting of labeled programs. This is based on the following key ideas. First, each piece of (encrypted) data that is outsourced is assigned a unique label which is used to identify the data. Second, whenever a client wants to ask the cloud to compute a function f on a portion of the outsourced (encrypted) data, the client specifies the inputs of f among the outsourced data. These inputs are identified by specifying their labels. The combination of f with these labels is called a labeled program. In short, labels allow clients to express queries on outsourced data.

In our homomorphic encryption notion, these ideas are introduced as follows. The encryption algorithm takes as input also a label; this is to say that the encryptor assigns a unique index to the encrypted data. Second, the decryption algorithm takes as additional input a labeled program; this is to express that the decryptor recovers the result of a known query (the labeled program) on the (unknown) outsourced data. In practice, the set of labels has concise representation (e.g. they can be names or even indexes in [1, n]).

Labeled Programs.  Here we recall the notion of labeled programs [15], adapted to the case of arithmetic circuits as in [5]. The definition is taken almost verbatim from [5]. A labeled program ${{\mathcal P}}$ is a tuple $(f,\tau _1, \ldots , \tau _{n})$ such that $f : \mathcal{M}^{n} \rightarrow \mathcal{M}$ is a function on n variables (e.g., a circuit), and $\tau _{i} \in \{0,1\}^{*}$ is the label of the i-th variable input of f.

Labeled Homomorphic Encryption.  A symmetric-key Labeled Homomorphic Encryption scheme labHE consists of the following algorithms.

• KeyGen $(1^\lambda )$. The key generation algorithm takes as input the security parameter $\lambda$. It outputs a secret key $\mathsf{sk}$ and a public evaluation key $\mathsf{epk}$. We assume that $\mathsf{epk}$ implicitly contains a description of a message space $\mathcal{M}$, a label space $\mathcal{L}$, and a class $\mathcal{F}$ of “admissible” circuits.

• Enc($\mathsf{sk},\tau ,m$). The encryption algorithm takes as input the secret key $\mathsf{sk}$, a label $\tau \in \mathcal{L}$ and a message $m \in \mathcal{M}$. It outputs a ciphertext C.

• Eval(). On input ${\mathsf{epk}}$, an arithmetic circuit $f : \mathcal{M}^t \rightarrow \mathcal{M}$ in the class $\mathcal{F}$ of “allowed” circuits, and t ciphertexts $C_1, \ldots , C_t$, the evaluation algorithm returns a ciphertext C.

• Dec($\mathsf{sk}, {\mathcal P}, C$). The decryption algorithm takes as input the secret key, a labeled program ${{\mathcal P}}$, and a ciphertext C, and it outputs a message $m \in \mathcal{M}$.

A labHE must satisfy correctness, succinctness, semantic security, and context-hiding.

Definition 1

(Correctness). A Labeled Homomorphic Encryption scheme $\mathsf{labHE} =(\mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ correctly evaluates a family of circuits $\mathcal{F}$ if for all honestly generated keys $(\mathsf{epk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(1^{\lambda })$, for all $f \in \mathcal{F}$, all labels $\tau _1, \ldots , \tau _t \in \mathcal{L}$, all messages $m_1, \ldots , m_t \in \mathcal{M}$, any $C_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Enc}(\mathsf{sk}, \tau _i, m_i)$ $\forall i \in [t]$, and ${\mathcal P}=(f, \tau _1, \ldots , \tau _t)$,

$$\Pr [\mathsf{Dec}(\mathsf{sk}, {\mathcal P}, \mathsf{Eval}(\mathsf{epk}, f, C_1, \ldots , C_t)) = f(m_1, \ldots , m_t)] = 1-\mathsf{negl}(\lambda ) \,.$$

Informally succinctness means that the size of ciphertexts output by $\mathsf{Eval}$ is some fixed polynomial in the security parameter, and does not depend on the size of the evaluated circuit. Formally, this is defined as follows.

Definition 2

(Succinctness). A Labeled Homomorphic Encryption scheme $\mathsf{labHE} =(\mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ is said to succinctly evaluate a family of circuits $\mathcal{F}$ if there is a fixed polynomial $p(\cdot )$ such that every honestly generated ciphertext (output of either $\mathsf{Enc}$ or $\mathsf{Eval}$) has size (in bits) $p(\lambda )$.

We note that our notion of succinctness is weaker than the notion of compactness of standard homomorphic encryption. Compactness dictates that the running time of the decryption algorithm is bounded by some fixed polynomial in $\lambda$. Succinctness is weaker in the sense that a compact scheme is also succinct whereas the converse might not be true (indeed our construction satisfies succinctness but not compactness).

The security of a labHE scheme is defined via a notion of semantic security that adapts to our setting the standard notion put forward by Goldwasser and Micali [17].

Definition 3

(Semantic Security for labHE ). Let $\mathsf{labHE} = (\mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ be a Labeled Homomorphic Encryption scheme and $\mathcal{A}$ be a PPT adversary. Consider the following experiment where $\mathcal{A}$ is given access to an oracle $\mathsf{Enc}(\mathsf{sk}, \cdot , \cdot )$ that on input a pair $(\tau , m)$ outputs $\mathsf{Enc}(\mathsf{sk}, \tau , m)$:

We say that $\mathcal{A}$ is a legitimate adversary if it queries the encryption oracle on distinct labels (i.e., each label $\tau$ is never queried more than once), and never on the two challenge labels $\tau ^{*}_{0}, \tau ^{*}_1$. We define $\mathcal{A}$’s advantage as $\mathbf {Adv}^{\mathsf{SS}}_{\mathsf{labHE}, \mathcal{A}}(\lambda ) := \Pr [\mathbf {Exp}^{\mathsf{SS}}_{\mathsf{labHE}, \mathcal{A}}(\lambda ) = 1] - \frac{1}{2}$. Then we say that $\mathsf{labHE}$ provides semantic-security if for any PPT legitimate algorithm $\mathcal{A}$ it holds $\mathbf {Adv}^{\mathsf{SS}}_{\mathsf{labHE}, \mathcal{A}}(\lambda ) = \mathsf{negl}(\lambda )$.

Finally we define another security property of Labeled Homomorphic Encryption called context-hiding, which says that a user running $m = \mathsf{Dec}(\mathsf{sk}, {\mathcal P}, C)$ learns nothing about the input $m'$, except that $m=f(m')$, where f is the function in ${{\mathcal P}}$.

Definition 4

(Context Hiding). We say that a Labeled Homomorphic Encryption scheme $\mathsf{labHE}$ satisfies context-hiding for a family of circuits $\mathcal{F}$ if there exists a PPT simulator $\mathsf{Sim}$ and a negligible function $\epsilon (\lambda )$ such that the following holds. For any $\lambda \in \mathbb N$, any pair of keys $(\mathsf{epk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(1^{\lambda })$, any circuit $f \in \mathcal{F}$ with t inputs, any tuple of messages $m_1, \ldots , m_t \in \mathcal{M}$, labels $\tau _1, \ldots , \tau _t \in \mathcal{L}$, corresponding ciphertexts $C_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Enc}(\mathsf{sk}, \tau _i, m_i)$ $\forall i=1, \ldots , t$, ${\mathcal P}= (f, \tau _1, \ldots , \tau _t)$ and $m = f(m_1, \ldots , m_t)$:

$$\mathsf{SD}[\mathsf{Eval}(\mathsf{epk}, f, C_1, \ldots , C_t), \; \mathsf{Sim}(1^{\lambda }, \mathsf{sk}, {\mathcal P}, m)] = \mathsf{negl}(\lambda )\,$$

Labeled Homomorphic Encryption  with Preprocessing.  Here we define a special case of Labeled Homomorphic Encryption where some of the algorithms allow for a preprocessing step that enables to speed up online computations.

We say that a scheme $\mathsf{labHE}$ has offline/online encryption if it admits two algorithms $\mathsf{Offline\text {-}Enc}$ and $\mathsf{Online\text {-}Enc}$ working as follows. Offline-Enc $(\mathsf{sk},\tau )$ takes a label and the secret key and produces an offline ciphertext $C_{\mathsf{off}}$ for $\tau$. Online-Enc $(C_\mathsf{off},m)$ takes a message m and an offline ciphertext for label $\tau$ and produces a ciphertext C. The two algorithms must be correct in the sense that $\mathsf{Enc}(\mathsf{sk},\tau ,m)$ equals the outcome of $\mathsf{Online\text {-}Enc}(\mathsf{Offline\text {-}Enc}(\mathsf{sk}, \tau ), m)$. Informally, the first algorithm is the computationally more costly procedure that can be run independently of the actual message one wishes to encrypt. Online-Enc, on the other hand, is more efficient but can be executed only when m becomes available.

A scheme $\mathsf{labHE}$ has offline/online decryption if it admits two algorithms $\mathsf{Offline\text {-}Dec}$ and $\mathsf{Online\text {-}Dec}$ as follows. Offline-Dec $(\mathsf{sk},{\mathcal P})$ takes a secret key and a labeled program and produces an offline secret key $\mathsf{sk}_\mathsf{off}$ for ${{\mathcal P}}$. Notice that $\mathsf{sk}_\mathsf{off}$ does not depend on a ciphertext. Online-Dec $(\mathsf{sk}_\mathsf{off},C)$ takes $\mathsf{sk}_\mathsf{off}$ and C and outputs a message m. Again, the two algorithms must be correct in the sense that $\mathsf{Dec}(\mathsf{sk}, {\mathcal P}, C)$ equals the outcome of $\mathsf{Online\text {-}Dec}(\mathsf{Offline\text {-}Dec}(\mathsf{sk}, {\mathcal P}), C)$. Offline/online decryption allows to split the decryption procedure into two parts: the offline one which is computationally more expensive and may depend on the complexity of the program ${{\mathcal P}}$; the online part that is much faster and whose running time is a fixed polynomial in the security parameter.

3 A Construction of Labeled HE for Quadratic Polynomials

In this section we present a construction of Labeled Homomorphic Encryption that supports the evaluation of degree-two polynomials. Our construction builds upon the technique of [6] for boosting linearly homomorphic encryption schemes to evaluate degree-two polynomials on ciphertexts. Interestingly, however, while the construction from [6] achieves succinctness only for the subclass of degree-two polynomials where the number of degree-two monomials is bounded by a constant, our realization achieves succinctness for all degree-two polynomials. Similarly to [6], our realization builds upon any (linearly) homomorphic encryption scheme that is public space (e.g., [25]). This property requires that the message space $\mathcal{M}$ is a (publicly known) commutative ring where it is possible to sample random elements efficiently (see [6] for a more rigorous definition).

Let $\mathsf{\hat{HE}}=(\mathsf{\hat{KeyGen}},\mathsf{\hat{Enc}},\mathsf{\hat{Eval}}, \mathsf{\hat{Dec}})$ be a public-space linearly-homomorphic encryption scheme (see [16] for the details). Following [6] we denote with $\mathcal{\hat{C}}$ the ciphertext space of $\mathsf{\hat{HE}}$, we use Greek letters to denote elements of $\mathcal{\hat{C}}$ and Roman letters for elements of $\mathcal{M}$. Without loss of generality we assume that $\mathsf{\hat{Eval}}$ consists of two procedures: one to perform (homomorphic) additions and another to perform (homomorphic) multiplications by constants. We denote these operations with $\boxplus$ and $\cdot$, respectively and (abusing notation) we denote addition and multiplication in $\mathcal{M}$ as $+$ and $\cdot$.

We propose a Labeled Homomorphic Encryption scheme $\mathsf{labHE} =(\mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ capable of evaluating multivariate polynomials of degree 2 over $\mathcal{M}$, with respect to some (finite) set of labels $\mathcal{L}\subset \{0,1\}^*$. We use a pseudorandom function $F : \{0,1\}^k \times \{0,1\}^* \rightarrow \mathcal{M}$, with key space $\{0,1\}^k$, for some $k=\mathsf{poly}(\lambda )$.

• $\mathsf{KeyGen}(1^{\lambda })$: On input a security parameter $\lambda \in \mathbb N$, run $\mathsf{\hat{KeyGen}}(1^{\lambda })$ to get $(\mathsf{pk},\mathsf{sk}')$. Next, choose a random seed $K \in \{0,1\}^k$ for the PRF, and set $\mathcal{L}= \{0,1\}^{*}$. Output $\mathsf{sk}=(\mathsf{sk}',K)$ and $\mathsf{epk}=(\mathsf{pk},\mathcal{L})$. The above assumes that $\mathsf{pk}$ already describes both $\mathsf{\hat{HE}}$’s message space $\mathcal{M}$ and its ciphertext space $\mathcal{\hat{C}}$. The message space of $\mathsf{labHE}$ will be $\mathcal{M}$.

• $\mathsf{Enc}(\mathsf{sk}, \tau , m)$: We describe $\mathsf{Enc}$ directly in terms of its two components Offline-Enc and Online-Enc.

  • Offline-Enc $(\mathsf{sk},\tau )$: Given a label $\tau$, compute $b \leftarrow F(K,\tau )$ and outputs $C_\mathsf{off}=(b,\mathsf{\hat{Enc}}(\mathsf{pk}, b))$.

  • Online-Enc $(C_\mathsf{off})$. Parse $C_\mathsf{off}$ as $(b,\beta )$ and output $C=(a,\beta )$, where $a \leftarrow m-b$ (in $\mathcal{M}$). Notice that the cost of online encryption is that of an addition in $\mathcal{M}$.

• $\mathsf{Eval}(\mathsf{epk}, f, C_1, \ldots , C_t)$: $\mathsf{Eval}$ is composed of 3 different procedures: $\mathsf{Mult}, \mathsf{Add}, \mathsf{cMult}$. We describe each such procedure separately. Informally, $\mathsf{Mult}$ allows to perform (homomorphic) multiplications, $\mathsf{Add}$ deals with homomorphic additions and $\mathsf{cMult}$ takes care of (homomorphic) multiplications by known constants.

  • $\mathsf{Mult}$: On input two ciphertexts $C'_1, C'_2 \in \mathcal{M}\times \mathcal{\hat{C}}$ where, for $i=1,2$, $C_i=(a_i, \beta _i)$, the algorithm computes a “multiplication” ciphertext $C=\alpha \in \mathcal{\hat{C}}$ as:

    $$\begin{aligned} \alpha= & {} \mathsf{\hat{Enc}}(\mathsf{pk}, a_1 \cdot a_2 ) \boxplus a_1 \cdot \beta _2 \boxplus a_2 \cdot \beta _1 \end{aligned}$$

    Correctness follow from the fact that, if $a_i=(m_i - b_i)$ and $\beta _i \in \mathsf{\hat{Enc}}(\mathsf{pk}, b_i)$ for some $b_i \in \mathcal{M}$, then

    $$\begin{aligned} \alpha\in & {} \mathsf{\hat{Enc}}\left( \mathsf{pk}, (m_1m_2 - b_1m_2 - b_2m_1 + b_1 b_2) +\right. \\&\quad \quad \left. (b_2m_1 - b_1b_2) + (b_1m_2 - b_1b_2) \right) = \mathsf{\hat{Enc}}(\mathsf{pk}, m_1m_2 - b_1b_2) \end{aligned}$$

  • $\mathsf{Add}$: We distinguish two cases depending on the format of the two input ciphertexts $C_1, C_2$. If $C_1, C_2 \in \mathcal{M}\times \mathcal{\hat{C}}$ where, for $i=1,2$, $C_i=(a_i, \beta _i)$, then the algorithm produces a new ciphertext $C=(a,\beta ) \in \mathcal{M}\times \mathcal{\hat{C}}$ computed as

    $$a=a_1 + a_2, \quad \beta = \beta _1 \boxplus \beta _2$$

    For correctness in this case note that if $a_i=(m_i - b_i)$ and $\beta _i \in \mathsf{\hat{Enc}}(\mathsf{pk}, b_i)$ for some $b_i \in \mathcal{M}$, then $a = (m_1+m_2) - (b_1 + b_2)$ and $\beta \in \mathsf{\hat{Enc}}(\mathsf{pk}, b_1 + b_2)$.

    If, on the other hand, the received ciphertexts are $C_1, C_2 \in \mathcal{\hat{C}}$ where, for $i=1,2$, $C_i=\alpha _i$, the new ciphertext $C=\alpha \in \mathcal{\hat{C}}$ is computed as $\alpha = \alpha _1 \boxplus \alpha _2$.

  • $\mathsf{cMult}$: As before, on input a constant $c \in \mathcal{M}$ and a ciphertext C, we distinguish two cases depending on the format of C. If $C=(a, \beta ) \in \mathcal{M}\times \mathcal{\hat{C}}$, this algorithm returns a ciphertext $C' = (a \cdot c, c \cdot \beta ) \in \mathcal{M}\times \mathcal{\hat{C}}$. If, on the other hand, $C=\alpha \in \mathcal{\hat{C}}$, this algorithm returns a ciphertext $C' = c \cdot \alpha \in \mathcal{\hat{C}}$.

    The correctness of the above operations is straightforward.

• $\mathsf{Dec}(\mathsf{sk},{\mathcal P}, C)$: As for the case of the encryption procedure, we describe the algorithm in terms of its two components Offline-Dec and Online-Dec.

  • Offline-Dec $(\mathsf{sk},{\mathcal P})$. Given $\mathsf{sk}$ and the labeled program ${{\mathcal P}}$, parse ${{\mathcal P}}$ as $(f, \tau _1, \ldots , \tau _t)$. For $i=1, \ldots , t$, the algorithm computes $b_i \leftarrow F(K,\tau _i)$, $b= f(b_1,\ldots , b_t)$ and outputs $\mathsf{sk}_{\mathcal P}=(\mathsf{sk}, b)$.

  • Online-Dec $(\mathsf{sk}_{\mathcal P}, C)$. Parse $\mathsf{sk}_{\mathcal P}$ as $(\mathsf{sk},b)$, we distinguish two cases depending on whether $C \in \mathcal{M}\times \mathcal{\hat{C}}$ or not.

    If $C=(a, \beta ) \in \mathcal{M}\times \mathcal{\hat{C}}$ there are two decryption methods: (i) output $m=a + b$; (ii) output $m = a + \mathsf{\hat{Dec}}(\mathsf{sk}, \beta )$.

    If $C \in \mathcal{\hat{C}}$ set $\hat{m}=\mathsf{\hat{Dec}}(\mathsf{sk},C)$ and output $m=\hat{m}+b$.

    Notice that the cost of online decryption solely depends on the cost of $\mathsf{\hat{Dec}}$ and it is totally independent of ${{\mathcal P}}$. Moreover the decryption method (ii) does not require the offline phase.

Succinctness of $\mathsf{labHE}$ follows easily from the compactness of the underlying linearly-homomorphic encryption. Correctness follows from a simple inductive argument on the structure of labelled programs: i. decryption of freshly encrypted ciphertexts is correct if the underlying $\mathsf{\hat{HE}}$ is correct; ii. to show that the encrypted output of a labelled program decrypts correctly, one establishes that individual gates will produce the correct result for all possible configurations of the input ciphertexts, distinguishing the cases that the input ciphertexts are fresh encryptions or the outputs of other gates.

Security.  The following two theorems prove that our $\mathsf{labHE}$ scheme satisfies semantic security and context hiding respectively.

Theorem 1

If $\mathsf{\hat{HE}}$ is semantically-secure and F is pseudorandom then $\mathsf{labHE}$ is semantically secure.

The proof is obtained via a simple hybrid argument. First, notice that if one modifies $\mathbf {Exp}^{\mathsf{SS}}_{\mathsf{labHE}, \mathcal{A}}(\lambda )$ so that the b’s corresponding to $\tau _0$ and $\tau _1$ are taken at random (rather than using F), then the resulting experiment is computationally indistinguishable from the original one, under the assumption that F is PRF. Afterwards, notice that

$$\begin{aligned}&(m_0 - b_0, \mathsf{\hat{Enc}}(\mathsf{pk}, b)) \approx (m_0 - b_0, \mathsf{\hat{Enc}}(\mathsf{pk}, 0)) \\&\equiv (m_1 - b_1, \mathsf{\hat{Enc}}(\mathsf{pk}, 0)) \approx (m_1 - b_1, \mathsf{\hat{Enc}}(\mathsf{pk}, b_1)) \end{aligned}$$

where $\approx$ denotes computational indistinguishability by the semantic security of $\mathsf{\hat{HE}}$ and $\equiv$ means that the distributions are identical.

Theorem 2

If $\mathsf{\hat{HE}}$ is circuit-private, then $\mathsf{labHE}$ is context-hiding.

Proof

We prove the theorem by showing the following simulator. Let $\hat{\mathsf{Sim}}$ be the simulator for the circuit privacy of $\mathsf{\hat{HE}}$. If f is a degree-1 polynomial the simulator $\mathsf{Sim}(1^{\lambda }, \mathsf{sk}, (f, \tau _1, \ldots , \tau _t), m)$ computes $b = f(F(K, \tau _1), \ldots ,$ $F(K, \tau _t))$ and outputs $C = (m - b, \hat{\mathsf{Sim}}(1^{\lambda },\mathsf{pk}, b))$. If f is of degree 2, the simulator does the same except that it computes $C = \hat{\mathsf{Sim}}(1^{\lambda },\mathsf{pk}, m - b)$. It is straightforward to see that by the circuit privacy of $\mathsf{\hat{HE}}$ C is distributed identically to the ciphertext produced by $\mathsf{Eval}$.

4 Multi-user Labeled HE

In this section we introduce a multi-user variant of Labeled Homomorphic Encryption. The main idea is that encryptors do not share a global common secret key. Rather, each user i employs his own secret key $\mathsf{usk}_i$ to encrypt, yet it is possible to homomorphically compute over data encrypted by different users. Decryption then requires knowledge of the master secret along with the public keys of all the users whose ciphertexts were involved in the computation.

A Multi-User Labeled Homomorphic Encryption scheme consists of a tuple of algorithms $\mathsf{mu\text {-}labHE} =(\mathsf{Setup}, \mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ working as follows.

• Setup $(1^\lambda )$. The setup algorithm takes as input the security parameter $\lambda$, and outputs a master secret key $\mathsf{msk}$ and a master public key ${\mathsf{mpk}}$. We assume that ${\mathsf{mpk}}$ implicitly contains a description of a message space $\mathcal{M}$, a label space $\mathcal{L}$, and a class $\mathcal{F}$ of “admissible” circuits.

• $\mathsf{KeyGen}(\mathsf{mpk})$. The key generation algorithm takes as input the master public key ${\mathsf{mpk}}$ and outputs a user secret key $\mathsf{usk}$ and a user public key $\mathsf{upk}$.

• $\mathsf{Enc}(\mathsf{mpk}, \mathsf{usk}, \tau , m)$. The encryption algorithm takes as input the master public key ${\mathsf{mpk}}$, a user secret key $\mathsf{usk}$, a label $\tau \in \mathcal{L}$ and a message $m \in \mathcal{M}$. It outputs a ciphertext C.

• Eval(). On input ${\mathsf{mpk}}$, an arithmetic circuit $f : \mathcal{M}^t \rightarrow \mathcal{M}$ in the class $\mathcal{F}$ of “allowed” circuits, and t ciphertexts $C_1, \ldots , C_t$, the evaluation algorithm returns a ciphertext C.

• Dec(). The decryption algorithm takes as input the secret key, a vector of user secret keys $\mathbf {\mathsf{upk}}= (\mathsf{upk}_1, \ldots , \mathsf{upk}_{\ell })$, a labeled program ${{\mathcal P}}$, and a ciphertext C, and it outputs a message $m \in \mathcal{M}$.

A Multi-User Labeled Homomorphic Encryption scheme is required to satisfy correctness, succinctness, semantic security, and context-hiding as defined below.

Definition 5

(Correctness). A Multi-User Labeled Homomorphic Encryption scheme $\mathsf{mu\text {-}labHE} =(\mathsf{Setup}, \mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ correctly evaluates a family of circuits $\mathcal{F}$ if for all honestly generated keys $(\mathsf{mpk}, \mathsf{msk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Setup}(1^{\lambda })$, all user keys $(\mathsf{upk}_1, \mathsf{usk}_1),$ $\ldots ,(\mathsf{upk}_{\ell }, \mathsf{usk}_{\ell }) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(\mathsf{mpk})$, for all $f \in \mathcal{F}$, all labels $\tau _1, \ldots , \tau _t \in \mathcal{L}$, messages $m_1, \ldots , m_t \in \mathcal{M}$, any $C_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Enc}(\mathsf{mpk}, \mathsf{usk}_{j_{i}}, \tau _{i}, m_i)$ $\forall i \in [t], j_i \in [\ell ]$ and ${\mathcal P}=(f, \tau _1, \ldots , \tau _t)$:

$$\Pr [\mathsf{Dec}(\mathsf{sk}, \mathbf {\mathsf{upk}}, {\mathcal P}, \mathsf{Eval}(\mathsf{pk}, f, C_1, \ldots , C_t)) = f(m_1, \ldots , m_t)] = 1-\mathsf{negl}(\lambda ) \,.$$

The notion of succinctness for multi-user Labeled Homomorphic Encryption is identical to that given in Definition 2. Security of Multi-User Labeled Homomorphic Encryption is defined similarly to that of labHE.

Definition 6

(Semantic Security for mu-labHE ). Let $\mathsf{mu\text {-}labHE} = (\mathsf{Setup}, \mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Eval}, \mathsf{Dec})$ be a Multi-User Labeled Homomorphic Encryption scheme and $\mathcal{A}$ be a PPT adversary. Consider the following experiment where $\mathcal{A}$ is given access to an oracle $\mathsf{Enc}(\mathsf{mpk}, \mathsf{usk}, \cdot , \cdot )$ that on input a pair $(\tau , m)$ outputs $\mathsf{Enc}(\mathsf{mpk}, \mathsf{usk}, \tau , m)$:

We say that $\mathcal{A}$ is a legitimate adversary if it queries the encryption oracle on distinct labels (i.e., each label $\tau$ is never queried more than once), and never on the two challenge labels $\tau ^{*}_{0}, \tau ^{*}_1$. We define $\mathcal{A}$’s advantage as $\mathbf {Adv}^{\mathsf{SS}}_{\mathsf{mu\text {-}labHE}, \mathcal{A}}(\lambda ) := \Pr [\mathbf {Exp}^{\mathsf{SS}}_{\mathsf{mu\text {-}labHE}, \mathcal{A}}(\lambda ) = 1] - \frac{1}{2}$. Then we say that $\mathsf{mu\text {-}labHE}$ has semantic-security if for any PPT legitimate algorithm $\mathcal{A}$ it holds $\mathbf {Adv}^{\mathsf{SS}}_{\mathsf{mu\text {-}labHE}, \mathcal{A}}(\lambda ) = \mathsf{negl}(\lambda )$.

Finally we adapt the notion of context-hiding of Labeled Homomorphic Encryption to the multi-user case. The intuitive meaning of the notion is the same.

Definition 7

(Context Hiding). A Multi-User Labeled Homomorphic Encryption scheme $\mathsf{mu\text {-}labHE}$ satisfies context-hiding for a family of circuits $\mathcal{F}$ if there exists a PPT simulator $\mathsf{Sim}$ and a negligible function $\epsilon (\lambda )$ such that the following holds. For any $\lambda \in \mathbb N$, any pair of master keys $(\mathsf{mpk}, \mathsf{msk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Setup}(1^{\lambda })$, any $\ell$ user keys $(\mathsf{upk}_1, \mathsf{usk}_1), \ldots ,$ $(\mathsf{upk}_{\ell }, \mathsf{usk}_{\ell }) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(\mathsf{mpk})$, any circuit $f \in \mathcal{F}$ with t inputs, any tuple of messages $m_1, \ldots , m_t \in \mathcal{M}$, labels $\tau _1, \ldots , \tau _t \in \mathcal{L}$, ciphertexts $C_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Enc}(\mathsf{mpk}, \mathsf{usk}_{j_i}, \tau _i, m_i)$ $\forall i=1, \ldots , t$ and $j_i \in [\ell ]$, ${\mathcal P}= (f, \tau _1, \ldots , \tau _t)$ and $m = f(m_1, \ldots , m_t)$:

$$\mathsf{SD}[\mathsf{Eval}(\mathsf{epk}, f, C_1, \ldots , C_t), \; \mathsf{Sim}(1^{\lambda }, \mathsf{msk}, \mathbf {\mathsf{upk}}, {\mathcal P}, m)] \le \epsilon (\lambda )\, .$$

In the full version [1] we show how to modify our construction to give an mu-labHE.

5 Statistics Using $\mathsf{labHE}$

In this section we show that by using our constructions of (multi-user) Labeled Homomorphic Encryption for quadratic polynomials, it is possible to compute relevant statistical functions over encrypted data. In the next Section we will then describe two application scenarios where the specific features of our protocol act as enablers for real-world applications. Intuitively, the restriction of computing only quadratic polynomials can be described as follows: suppose a value x and a value y are secret and are encrypted using our scheme. Then, one can compute any polynomial of the form $a_1x^2+a_2y^2+a_3xy +a_4x+a_5y+a_6$. More generally, given an arbitrary number of encrypted values, possibly coming from many users, one can compute any function that can be expressed as a linear function of those values and pairwise products between those values. We will see a few interesting examples of this next.

Consider a dataset as a matrix $X = \{x_{i,j}\}$, for $i=1, \ldots , n$ and $j=1, \ldots , d$. Number d represents the dimension (i.e., the number of variables/columns) while n is the number of dataset members (or rows).

Mean and Covariance.  First, we show how to compute the mean and covariance over a multidimensional dataset X. It is not hard to see how to extend these ideas to the computation of any other function that can be represented with a degree-2 polynomial. Such functions include, e.g., the root mean square (RMS), and the Pearson’s and uncentered correlation coefficient. The mean of the j-th column is the value $\mu _{j} = \frac{1}{n}\sum _{i=1}^{n} x_{i,j}$. Since our labHE does not support division, we compute homomorphically the value $\hat{\mu }_{j} = \sum _{i=1}^{n} x_{i,j}$ and let the receiver do the division after decryption. This is natural in scenarios where the computation conducted over the data is known to the decryptor, which is something that labelled homomorphic encryption implicitly assumes.

For a dataset X, its covariance matrix $C = \{c_{j,k}\}$ for $j,k=1,\ldots , d$ is defined as

$$c_{j,k} = \frac{1}{n} \sum _{i=1}^{n} x_{i,j} \cdot x_{i,k} - \frac{1}{n^2} \left( \sum _{i=1}^{n} x_{i,j}\right) \left( \sum _{i=1}^{n} x_{i,k}\right) $$

Again we will use the scheme to compute homomorphically the integers

$$\hat{c}_{j,k} = n^2 \cdot c_{j,k} = n \sum _{i=1}^{n} x_{i,j} \cdot x_{i,k} - \left( \sum _{i=1}^{n} x_{i,j}\right) \left( \sum _{i=1}^{n} x_{i,k}\right) $$

and let the receiver obtain $c_{j,k}$ by doing a division by $n^{2}$ after decryption.

Weighted Sum.  Given a dataset $X = \{x_{i,j}\}$ and a vector of weights $\mathbf {y} = \{y_i\}_{i=1}^{n}$, the weighted sum of the j-th column of X is the value $\omega _{j} = \sum _{i=1}^{n} x_{i,j} \cdot y_{i}$.

There are two situations to consider. If the weights are not secret, then the weighted sum can be expressed as a degree-1 polynomial over the encrypted column X. If, on the other hand, the vector of weights is itself secret, then the weighted sum becomes a degree two polynomial (an inner-product) between two vectors of encrypted values. We will see in the next section how this can be useful for genenetic association tests.

Euclidean Distance.  Given a matrix $X = \{x_{i,j}\}$ the (square of) Euclidean distance between the j-th column of X and a vector $\mathbf {y} = \{y_i\}_{i=1}^{n}$ is the value $\delta _j = \sum _{i=1}^{n} (x_{i,j} - y_i)^2$. This is an example of a function that requires a quadratic computation if either part of the data set is encrypted.

6 Applications and Evaluation

We implemented our (multi-user) labHE realization in C, and we evaluated its performance in two applications. In what follows we discuss the applications and present the experimental results. We refer to the full version [1] for more details.

6.1 Implementation and Micro-Benchmarks

We implemented our (multi-user) labHE realization in C starting from the GNU Multiprecision Library¹ (GMP) and the Kekkac Code Package² (KCP). We used GMP to implement the linearly homomorphic encryption scheme by Joye and Libert [20] (JL13) and relied on Sponge-based pseudorandom function included in the KCP. The JL13 cryptosystem has message space $\mathbb {Z}_{2^k}$ and works over $\mathbb {Z}^*_N$, where $N=pq$ is the product of two quasi-safe primes $p=2^{k}p'+1$ and $q=2^{k}q'+1$. For security [20] k needs to be at most $1/4 \log N - \lambda$, where $\lambda$ is the security parameter. Note that taking message space $\mathbb {Z}_{2^{k}}$ allows to perform computations over the integers with k-bits precision, and also to encode real values by using fixed point representations with suitable scaling as described, e.g., in [8]. Although our implementation is flexible, we fixed the security level at that of 2048 RSA moduli, conjectured to correspond to roughly 100–112 bits of security. All our implementations are single-threaded. Our benchmarking results were collected in a standard MacBook Pro machine with a 2.7 GHz Intel Core i5 and 16 GB or RAM. For every chosen set of parameters, we repeated the experiment 10 times, and took the median of the timings. In all cases we observed a coefficient of variation below $10\%$. For comparison with SHE we used the FV implementation in SEAL 2.0 [24] configured to support the same functions and security level.

Micro-Benchmarks.  Regarding communication/storage costs, every ciphertext of our scheme, instantiated with the above parameters can be encoded into 272 bytes. For instance, if we consider a dataset with $n=2^{20}$ rows and $d=2$ columns, it means that a server has to store about 560 MBytes. We now turn to the timings of basic operations such as key generation, encryption and decryption of level-1 ciphertexts (i.e., outputs of degree-1 functions, such as Mean). Collected timings are 155.11 ms for key generation, 0.35 ms for Encryption and 3.42 ms for decryption. Notably, while key generation is relatively relevant (it is executed only once), the speed in the encryption procedure (that is executed for every dataset item) is way more relevant for scalability. For a large data size such as the one above, encryption can be done in 12 min in a modest machine.

6.2 Outsourcing Privacy Preserving Statistics

Consider the case where a large dataset is stored on an (untrusted) Cloud. The latter is used both to store and to perform computations on encrypted data on behalf of one (or more) Clients. More precisely we considered two scenarios. One where the Client acts both as Data Provider and Receiver and a three party scenario where these roles are played by different users/entities. Of course, a solution to the problem of computing secure statistics in these scenarios can be obtained via somewhat homomorphic encryption schemes supporting quadratic polynomials. labHE, however, achieves the same goal with unprecedented efficiency both in terms of computation costs and in terms of bandwidth consumption. In our experiments, we considered multidimensional datasets represented as $(n\times d)$ matrices $X=\{x_{i,j}\}$, where n are the dataset members and d the dimension (or number of variables). Univariate statistics such as Mean and Variance are computed column-wise (e.g., the mean of the j-th column is $\mu _j=\frac{1}{n}\sum _{i=1}^n x_{i,j}$), whereas bivariate correlation ones such as Covariance act over pairs of columns. In this setting, if we consider a dataset of over two million entries ($n=2^{20}\times d=2$) that are 32-bit integers, the solution based on the FV somewhat homomorphic encryption requires over 249 GB of storage at the Cloud whereas labHE(JL13) only 560 Mbytes. Moreover, for such large datasets the amount of memory required to perform homomorphic computations using FV placed it out of reach of the standard machines we used for benchmarking (scalability is bounded at around 30K elements for 16 GB of RAM) while labHE(JL13) scaled up easily to two million entries. When considering the more modest datasets (where FV could run) the cumulative time of computing a Covariance matrix on the encrypted dataset and decrypting its result is 32 min using FV and 37 s with labHE(JL13); computing and decrypting a Mean query takes about 9 s with FV and around 19 ms with labHE(JL13).

6.3 Privacy Preserving GAS

Genetic Association Studies (GAS) look for statistically relevant features across the human genome, singling out those that can be correlated to given traits. Typically such studies are carried by performing series of tests. Each test targets a particular trait and takes into consideration associated information that is encoded in specific positions of an individual’s genome, the so-called Single Nucleotide Polymorphisms (SNP). Each test computes a Genetic Risk Score: a weighted sum of the information collected for each SNP and the weights correspond to risk estimates computed for a reference population [23]. This SNP genotyping has already several applications, ranging from personalized medicine to forensics. Access to such tests is, for the most part, controlled by the health services of different countries, but a new trend of Direct-to-Consumer (DTC) genomic analysis is arising, where companies offer a multitude of association tests to the public. Privacy is obviously a paramount concern in such services.

In this paper we propose a system for a Secure Direct-to-Consumer GAS, based on our Multi-User Labeled Homomorphic Encryption. Its architecture is presented in Fig. 2 (the colors represent trust domains), and roughly works as follows. The Patient wishes to be tested by the GAS service and trusts a Certified Genotyping Institution (CGI) to analyse a biological sample s, extract SNP information $G_s$, correctly encrypt it under the Patient’s public key $\mathsf {pk}$ using mu-labHE, and then erase all of the SNP-related information.³ The GAS is trusted by the Patient to correctly encrypt the test parameters P and send them to the Cloud. Next, the Cloud can compute the Genetic Risk Score on the encrypted data, and send this (encrypted) result to the Patient.

Fig. 2.

Architecture of a Secure Direct-to-Consumer GAS.

The threat model considered in our solution assumes that both the GAS and the Cloud are honest-but-curious. The GAS is trusted to follow a set of rules of the protocol, but not trusted to learn the genetic data of the Patient—even if it colludes with the Cloud. The Cloud is trusted by the GAS not to reveal the encrypted test parameters to the Patient, and is trusted by the Client to correctly perform the computation (over encrypted data). Note that the Cloud is not trusted by the Client to learn genetic data, and it may also be assumed to collude with the GAS, which means that this trust model is compatible with the most likely scenario that the GAS owns or contracts the Cloud service itself, and uses it to provide a service to the Patient. Under this threat model, we argue that: i. the semantic security of our mu-labHE ensures that no information about the encrypted data is leaked, except for its length; and ii. context hiding ensures that even the Patient, with knowledge of his secret key, obtains no information about the (possibly proprietary) test parameters P provided by the GAS. Details follow.

Security Analysis.  The total number of SNPs that have been documented up to date in the human genome is in the range of 150M. However, only a very small fraction of those, under 100K, has been looked at from a clinical analysis point of view⁴ and, indeed, the number of medical conditions that have been scientifically related to a Genetic Risk Score is around 5000.⁵ Furthermore, specific association tests, e.g., for a medical condition, will focus on a very small number of SNPs ranging from 1 or 2, to at most a few hundred and a safe estimate is that, over all current association tests, each of them will on average look at 50 SNPs. This places the number of clinically relevant SNPs, at present, at around 30K. This is roughly the number of SNPs that one needs to look at in order to evaluate all the Genetic Risk Scores that have been associated with a medical condition. We assume that there is a predefined set $\mathcal {L}$ of all positions (loci) of relevant SNPs, which is public and known by all parties. This could be the union of all positions that the GAS may test in all of its analyses—if this is not sensitive information from the point of view of the GAS—or it may be a larger set of all positions of SNPs that are known to be clinically relevant by the scientific community. In the first case we would have $|\mathcal {L}|$ in the range of a few hundred, and in the second case we would have $|\mathcal {L}|$ in the range of the 30K, as things stand today [9, 19]. Under these assumptions, our solution guarantees that nothing is leaked about the genetic information of the Patient nor about the concrete parameters used by the GAS to perform its tests. Furthermore, if one sets $\mathcal {L}$ to include all clinically relevant SNPs, then no-one except the Patient and the medical center defining the tests will learn which traits are being tested—crucially this means that all access patterns over the stored genome data are kept private. Otherwise, it will be publicly known that the Patient was tested at positions relevant for a specific GAS.

Although this approach may seem wasteful of resources, this is essential to ensuring that the Cloud (or some external observer) can infer nothing from an encrypted version of $G_s$ and P, in addition to the public set $\mathcal {L}$ itself, under the assumption that the encryption scheme is semantically secure. Furthermore, as we will see in our experimental evaluation, the efficiency of our homomorphic encryption scheme works as an enabler for this level of security, as it permits performing computations in reasonable time.

Benchmarks.  Figure 3 shows the timing data we collected when evaluating our protocol on data sets of increasing sizes. The offline encryption and decryption times increase linearly with the number of SNPs, although the offline decryption time is under 90 ms even for 30000 SNPs, whereas the off-line encryption time gradually grows up to 45 s. The overall decryption time, even accounting for the preprocessing is very light: note that on-line decryption takes constant time in the range of 3 ms. Online encryption time, on the other hand is very fast, and can be done in under 24 ms even for 30000 SNPs. Finally, the homomorphic computation in the cloud, grows linearly with the number of points, and it is reasonably small, clearly in the range of practicality, and even using a single modest server and no parallelism. In our machine, the processing time was around 47 s for a risk analysis involving 30000 SNPs. We recall that this was the estimated worst case scenario for the union of SNPs corresponding to all GAS-relevant information known to today. The size of the encrypted data processed by the cloud is, in this case, 32 MByte, half of it produced by the Patient and half by the medical centre.

Fig. 3.

Timings for various algorithms in secure GAS protocol for increasing numbers of SNPs.

To evaluate the scalability of our solution we considered a Map-Reduce scenario where the multiplicative part of the weighted sum is split by multiple servers in the Cloud. In this way many partial sums can be computed in parallel and later combined to get the final result. Using this strategy, a GAS computation including over 1 million SNPs can be completed in roughly 3 min using 10 servers (excluding communication overhead). Using FV [13], as underlying building block for a risk analysis involving only 30K SNPs the size of encrypted data processed by the Cloud becomes, roughly, 14 GBytes, which is over 400 times more than the space required by our solution. For the same task, FV-based solutions turn out to be around 100 times slower than our solution. This comparison is for a modest number of SNPs since, for larger parameters, experiments became highly unstable and eventually infeasible due to too large memory requirements that surpassed the capabilities of our benchmarking platform.

7 Conclusions

We presented a new methodology for processing remotely outsourced data in a privacy preserving way via the notion of Labeled Homomorphic Encryption. We showed an efficient realization and implementation of this primitive that targets computations described by degree-2 polynomials, with applications to executing statistical functions on encrypted data. Our experiments confirmed the practicality of our solution showing that it outperforms solutions based on somewhat homomorphic encryption. Our current solutions achieve privacy against a honest-but-curious Cloud server. In order to achieve security against malicious servers, one can use verifiable computation protocols in a generic fashion, as explained in [14]. Unfortunately, applying this idea generically to our schemes does not yield an efficient solution. Informally this is because modeling algebraic operations over $\mathbb {Z}_N^{*}$ is expensive when using state-of-the-art VC protocols (such as [26]). Designing an ad-hoc verifiable computation mechanism for our schemes while preserving efficiency is therefore a promising future direction for this work.