1 Introduction

Arterial spin labelling is an MR imaging technique that offers quantitative, noninvasive measurements of blood flow in the brain and other organs of the body, and has great promise as a biomarker for several diseases [1]. Unfortunately, ASL has low SNR, making it necessary to acquire large amounts of data to achieve accurate perfusion measurements. Spatial regularisation can improve the effective SNR by accounting for the inherent spatial correlation in perfusion: nearby voxels are likely to have similar perfusion values. Single inversion time ASL is by far the most commonly used type of ASL, however spatial regularisation for it is mostly limited to Gaussian smoothing with an arbitrarily-chosen kernel size. This is problematic: it introduces an unnecessary extra parameter (the kernel size), it causes a loss of fine detail in the image (crucial within gray matter), and it fails to account for the tissues and signal model underpinning the data.

In this work, we propose a novel method for single inversion time spatial regularisation in which anatomical information from structural images is used in a data-driven, Bayesian approach. We use a hierarchical prior in conjunction with \(T_1\) parcellations, directly improving perfusion estimation in ASL data. This not only improves individual perfusion images, but also improves confidence in detection of group perfusion differences. We validate our method in a cohort of preterm-born adolescents and age-matched controls (N = 130), both by performing test-retest experiments and by showing our method is better at identifying inter-group differences. Our method does significantly better in both, showing its potential to improve processing in single inversion time ASL studies.

2 Methods

2.1 Arterial Spin Labelling

In ASL, blood is magnetically “tagged” by inversion pulse at the neck before delivery to the brain – by acquiring images with and without this tagging, one effectively measures the difference that the blood flow makes to the signal. By use of a standard ASL signal model [2], the measured difference images can be related to the underlying perfusion, f. That is, \(y = g(f) + e\), where y are the measured images, e is Gaussian noise of unknown magnitude, and g is given by

$$\begin{aligned} g(f) = \frac{2 \alpha SI_{PD}}{6000 \lambda } \frac{T_{1b} \left( 1 - \exp {\frac{-\tau }{T_{1b}}}\right) }{\exp {\frac{-PLD}{T_{1b}}}} f \end{aligned}$$
(1)

where \(\tau \) is the label duration, PLD is the post-label delay, \(SI_{PD}\) is the proton density image, and other symbols have standard meanings and values [1]. For 2D acquisitions, PLD is usually slice-dependent.

2.2 Spatial Regularisation

Because of the inherently low SNR of ASL, it is common to perform spatial regularisation on the data – relying upon the similarity of the perfusion in nearby voxels to inform the parameter estimation process, effectively boosting the SNR. Typically, this is done by smoothing with a Gaussian kernel [3], and leads to significant improvements in the quality of ASL images. Unfortunately, this approach requires the arbitrary user-defined choice of a smoothing parameter (the kernel standard deviation), with an inevitable trade-off between SNR boost and loss of fine detail. Moreover, this approach makes no account of the underlying tissue types and signal model, information which drastically improves the quality of parameter estimation in multiple inversion time ASL and other imaging modalities [3, 4]. Although there are more statistically principled methods [3], these are only applicable to multiple inversion time ASL, where the full kinetic curve information is available [3]. In practice, single inversion time ASL is far more commonly used, and is the recommended implementation of ASL [1], so Gaussian smoothing remains overwhelmingly the most common approach.

In this work, as well as comparing our method with voxelwise fitting (no spatial regularisation), we also compare it with Gaussian smoothing at a variety of kernel sizes, from \(\sigma =1\,\text {mm}\) to 4 mm. This represents the range of realistic smoothing widths: for ASL, which focuses on the cortex, 1 mm is a comparatively narrow kernel, having a relatively subtle effect; 4 mm is a comparatively wide kernel, significantly blurring fine details in the data.

2.3 Anatomy-Driven Modelling

Our method uses a hierarchical prior in which spatial correlation is introduced by modelling regions as containing voxels with similar values. Parameter inference incorporates this correlation, resulting in large-scale spatial smoothness to the extent supported by the data. To define the regions in this work, we use lobar parcellations derived from \(T_1\) images, although our method could use any parcellation. A related approach, albeit with manually defined regions of interest and a different statistical model, significantly improved parameter estimation in IVIM diffusion [4]. In our method, the ASL signal model is used, and regions are derived systematically from an automated parcellation rather than manually.

We begin from the data likelihood for a voxel, index i, with ASL measurements \(y_{i,:}\) where \(\mathcal {N}\) is a normal distribution and \(\mathcal {MVN}\) is a multivariate normal:

$$\begin{aligned} p(y_{i,:} | f_i, \sigma _n) = \prod _j \mathcal {N}(y_{i,j}; g(f_i), \sigma _n) = \mathcal {MVN}(y_{i,:} - g(f_i) \mathbbm {1}, \sigma _n^2\mathbbm {I}) \end{aligned}$$
(2)

As the noise standard deviation, \(\sigma _n\), is unknown, we marginalise over it: \(p(y_{i,:} | f_i) = \int _0^\infty p(y_{i,:} | f_i, \sigma _n) p(\sigma _n) d \sigma _n\). We use a conjugate inverse gamma prior, \(p(\sigma _n) = \mathcal {IG}(\sigma _n^2; \alpha , \beta )\), later intentionally setting \(\alpha ,\beta \rightarrow 0\) to make the prior noninformative. Reparameterising and combining these, where \(\mathcal {NIG}\) is normal-inverse-gamma and \(t_\nu \) is a multivariate t-distribution with \(\nu \) degrees of freedom:

$$\begin{aligned} p(y_{i,:} | f_i) = \int _0^\infty \mathcal {NIG}(y_{i,:} - g(f_i)\mathbbm {1}, \sigma _n^2 \mathbbm {I}, \alpha , \beta ) d\sigma _n^2 = t_{2\alpha }(y_{i,:} - g(f_i)\mathbbm {1}, \frac{\beta }{\alpha }) \end{aligned}$$
(3)

Next we introduce the hierarchical prior structure: we assume that each region (throughout this work a lobe of the cortex) contains several voxels with normally distributed perfusion values. The hyperparameters \(\mu \) and \(\sigma \) are unknown for this distribution, so we use a noninformative Jeffreys hyperprior to make them wholly data-driven: \(p(\mu ,\sigma ) = \frac{1}{\sigma ^3}\). Applying Bayes’ theorem, the joint posterior distribution for a region containing N voxels, \(p(f_{1:N}, \mu , \sigma | y_{1:N,:})\), is proportional to \(\prod _{i=1}^N \left\{ p(y_{i,:} | f_i) p(f_i | \mu , \sigma )\right\} p(\mu , \sigma )\).

We use a Monte Carlo Markov Chain approach to perform inference on the per-voxel perfusion, \(f_i\), as well as the per-region distribution hyperparameters, \(\mu \) and \(\sigma \), using Gibbs sampling. This is initialised with least squares estimates, and over 100,000 iterations (1,000 discarded for burn-in), yields robust estimates on a timescale of tens of minutes using a modern laptop.

2.4 Validation

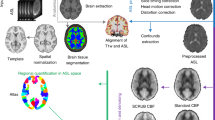
We use ASL images from 130 19-year-old subjects, 81 born extremely preterm (F/M = 48/33, <26 wks gestation) and 49 term-born peers (F/M = 31/18). Images were acquired on a 3T Phillips Achieva with 2D EPI pseudo-continuous ASL using 30 control-label pairs, PLD = 1800 ms + 41 ms/slice, \(\tau =1650\,\text {ms}\), \(3\times 3\times 5\,\text {mm}\). We also acquired \(SI_{PD}\) images and 3D \(T_1\)-weighted volumes at 1 mm isotropic resolution for segmentation and parcellation. Analysis is restricted to gray matter, masked by thresholding the segmentation at 0.8. We fit perfusion with the NiftyFit package [5] for voxelwise and Gaussian smoothing methods, and we use a MATLAB implementation of our method. We use a pre-existing tool to derive lobar parcellations [6]. Example images are shown in Fig. 1.

Fig. 1.
figure 1

Example images from term-born (top) and preterm-born (bottom). Left to right: \(T_1\)-weighted image, parcellation used to extract lobes, proton density (\(SI_{PD}\)), gray matter perfusion-weighted image (average of difference images).

Full size image

Because there is no ground truth data available, we perform test-retest experiments by splitting the difference images in half for each subject (first 15 difference images, second 15 difference images). For each subject the test-retest correlation, \(\rho \), is evaluated as the correlation between the estimated per-voxel f values in each half of the data, over all gray matter voxels. We also examine the perfusion maps to check that no method introduces obvious bias in the f estimates. If a regularisation method increases test-retest reproducibility without introducing bias, that method is likely providing more accurate estimates.

Subsequently, to assess how regularisation affects the analysis of perfusion data, we test for differences between groups after fitting the whole data set. We compare estimated perfusion between several groups: preterm-born versus term-born, male versus female, and subjects born via Caesarean section versus subjects delivered vaginally. We examine how regularisation affects the p value and confidence interval. When testing two methods on the same data, a decreased p value directly corresponds to a confidence interval suggesting a larger effect (centered further from zero). If p decreases on what is believed to be a genuine difference between groups, it suggests improved performance.

3 Results

3.1 Test-Retest Reproducibility

Figure 2 shows the distribution of per-subject test-retest correlation coefficients for each method. Our method has a significantly higher test-retest correlation than voxelwise fitting (voxelwise: \(\rho =0.57\), ours: \(\rho =0.73\); \(p={1.4\times 10^{-9}}\)) and any of the Gaussian kernels (\(p < 0.01\) for all, \(\rho =0.59\) to \(\rho =0.64\)). Figure 2 also shows the distribution of average gray matter perfusion values over all subjects, for each method. There are no significant differences in perfusion between any of the methods (\(p > 0.05\) for each pairwise t-test), suggesting no method introduces bias relative to voxelwise fitting. Conversely, there are significant differences in variance between our method and all other methods (\(p < 0.01\) for each pairwise F-test, our method has \(\sigma =10.2\,\text {ml/100\,g/min}\), other methods have \(\sigma =7.8\,\text {ml/100\,g/min}\) to \(\sigma =8.0\,\text {ml/100\,g/min}\)), and there are no significant differences in variance between any of the other methods.

Fig. 2.
figure 2

Left – distributions of test-retest correlation coefficients for each method. Right – distributions of average gray matter perfusion for each method.

Full size image

3.2 Qualitative Image Validation

Figure 3 shows a representative axial slice from a single subject, the perfusion estimates fitted using no spatial regularisation (voxelwise fitting), Gaussian smoothing with different kernel widths, and our method. All resulting perfusion maps are broadly similar, as would be expected – no method introduces noticeable bias in the image. As the kernel width is increased in Gaussian smoothing, the perfusion map becomes flatter, losing fine detail, especially at the largest kernel size (\(\sigma =4\,\text {mm}\)). In our method, conversely, fine spatial detail is preserved, although the parameter map is appreciably smoother than when no regularisation is applied. Figure 3 also shows how the choice of spatial regularisation affects the test-retest difference. Our method has smaller test-retest differences than Gaussian smoothing, as well as introducing less spatial correlation into the differences than the larger kernel sizes, particularly \(\sigma =4\,\text {mm}\).

Fig. 3.
figure 3

Example axial slice, for each regularisation method. The top row shows estimated perfusion, and the bottom row shows test-retest difference.

Full size image

3.3 Group Statistics

Figure 4 shows the average gray matter perfusion estimated by each method for each group: male/female, preterm/term, Caesarean/vaginal delivery. Figure 4 also shows the p value from a t-test for difference between the groups, for each method. Taking a threshold of \(p=0.05\), all methods agree on which groups have differences. There are significant differences between preterm males and females, with females having higher perfusion (Fig. 4a); and between term-born versus preterm-born, with preterm-born having lower perfusion (Fig. 4c). The latter result remains when the comparison is done for either sex.

Although the differences are significant under all methods, the confidence interval is centered further from zero (equivalently, more certain of an inter-group difference) for our method. For the perfusion difference between males and females, all preterm, the 95% confidence intervals are (all in \(\text {ml/100\,g/min}\)): voxelwise \({-7.9}/{1.1}\), 1 mm \({-7.6}/{1.2}\), 2–\(4\,\text {mm}\) \({-7.7}/{1.1}\), proposed \({-11.2}/{-1.4}\). Similarly, for preterm-born versus term-born, the intervals are: voxelwise 1.3/9.7, 1 mm 1.2/9.6, 2 mm 1.2/9.6, 3 mm 1.2/9.7, 4 mm 1.3/9.7, proposed 3.7/11.6.

Fig. 4.
figure 4

Distributions of gray matter perfusion for different groups of subjects under each regularisation method, with t-test p values for significant differences.

Full size image

4 Discussion and Conclusions

As shown in Fig. 2, our method significantly improves test-retest correlation coefficients over all 130 subjects. Moreover, the average gray matter perfusion value is not significantly different for any method, suggesting no method introduces bias. Our method does have larger variance in perfusion, which likely results from its capability to regularise the images without flattening them as in Fig. 3, and hence to more reliably detect extreme values which would otherwise be hidden by noise and misinterpreted as outlying values. These results are supported by Fig. 3, which shows example parameter maps and test-retest differences for each method. The perfusion maps are qualitatively similar to those estimated by voxelwise fitting with no regularisation, with smoothing levels visually similar to narrow kernel smoothing. Conversely, our method has visibly smaller test-retest differences than other regularisation techniques – this argues in favour of our method’s superiority to smoothing at any realistic kernel size.

The improved performance of our method, relative to Gaussian smoothing, is further supported by the analysis of group differences in Fig. 4. All methods agree on where there are significant differences between groups. Where there are differences, however, our method identifies these with a significantly lower p value: for example, in male versus female preterm-born subjects, \(p={6.7\times 10^{-4}}\) for our method versus \(p={0.020}\) for the best smoothing result. This shows in the confidence intervals, which are centered further from zero (more able to detect the difference) for the significant inter-group differences, as discussed in Sect. 3.3. The improvement in confidence intervals argues that our method improves perfusion analysis: it more reliably distinguishes differences for a given sample size. Figures 4b and d further support this interpretation: where there is no evidence of differences between groups’ perfusion, our method offers similar p values, showing sensitivity has not been increased at the cost of specificity.

Future work will extend the method to model partial volume effects, which have been given a principled treatment for multiple inversion time ASL [7] but remain challenging in single inversion time ASL [8], where partial volume modelling is not explicitly separated from spatial regularisation and existing methods make several strong assumptions concerning spatial correlation. Another promising avenue of future work is to explore the use of different regions in the hierarchical prior: currently lobar parcellations are used, but our method is not bound to any one parcellation. One could define regions based on any of the numerous parcellations derived from anatomy or watershed, according to what is most appropriate for the analysis. Given the heterogeneity of the cortex’s structure, it seems likely that more fine-grained regions could give even better results.

The novel Bayesian spatial regularisation approach presented here allows structural images to inform the analysis of perfusion data. It provides a principled, data-driven means of smoothing ASL data, removing the need for arbitrarily-set kernel parameters in existing techniques. Crucially, our method works on single inversion time ASL [1], meaning it is applicable to standard ASL implementations. It significantly improves test-retest reproducibility and statistical power for detecting group differences, which together are strong evidence of superiority to Gaussian smoothing. We believe this spatial regularisation technique could not only improve the quality of individual images, but could improve the statistical power of studies using ASL, allowing more reliable detection of perfusion differences with a smaller number of experimental subjects.