Keywords

1 Introduction

Nowadays the most suitable procedures for diagnosis in angiographic imaging are based on computed tomography (CT) and magnetic resonance (MR) (see [2]). The radiologist has full access to the 3D image volume and can perform 3D reconstructions. This provides not only a sophisticated visualization of the vascular tree, but also, some quantitative morphometric information about the diameters, cross-sectional areas, or volumes of vessel segments. However, before obtaining such measures, a segmentation step is required in order to extract the blood vessel segment of interest from the original set of slices.

There are several ways to perform full 3D segmentations of the aortic lumen and compute the centerline and the aorta cross-sections from these segmentations. In practice all these procedures require several time-consuming interactions with the user, especially if the aorta includes significant angulation in its morphology, which is the case when severe elongations are present. There are also some techniques which aim to extract directly the vessel centerline (see [9]). Most of these methods use local second-order differential features to compute the vessel centerline (see for instance [5, 6] or [8]). In the case of the aortic lumen, which has a large thickness, these methods based on local features do not provide an accurate estimation of the aorta centerline. In [10], the authors propose a method to track the centerline in the aortic lumen by fitting a local cylindrical structure of a fixed size to the aortic lumen using a pre-segmentation of the 3D image. The method is only checked in normal aortas, where large angulations are not present.

In this paper we present a new approach for aortic lumen tracking based on two main ideas: first, the contour of the aorta is approximated to an elliptical shape. Second, the tracking of the aortic lumen is performed by the optimization of the 3D orientation of the cross-sections of the aorta. The procedure starts by fixing a seed point inside the aortic lumen and the direction of scan (upward or downward). Then the "best" cross-sectional plane orientation of the aortic lumen that includes the seed point is obtained according to an energy optimization criterion which aims to minimize the area and eccentricity of the ellipse. To estimate the ellipse in each cross-sectional plane we use the method introduced in [1], based on the minimization of the energy

$$\begin{aligned} E_{1}(C,\mathcal {I},\sigma )=\frac{1}{|C|}\oint _{C }\nabla G_{\sigma }*\mathcal {I}(C(s))\cdot \bar{n} (s)ds, \end{aligned}$$
(1)

where \(\mathcal {I}\) is a 2D image, C represents the ellipse and \(G_{\sigma }\) is a Gaussian convolution kernel with standard deviation \(\sigma \). The above line integral measures the contrast of the convolved image along the ellipse and the local extrema of such energy are attained for ellipses fitting high-contrast contours. This energy is a simplification of the one introduced in [1], where some double integral terms are also included. Active contour models are a widely used technique in medical imaging. In [4], the authors present a general introduction to the applications of active contours to bioimage analysis. In [3] the authors propose a combination of contour and region based snake models in the context of muscle fiber image analysis. An energy similar to (1) has been proposed in [7] for parametric snakes.

The rest of the paper is organized as follows: In Sect. 2, we present the proposed energy-based method to track the aortic lumen geometry. In Sect. 3, we present some experiments and in Sect. 4, we present the main conclusions.

2 Energy Model to Compute the Orientation of the Cross-sectional Plane

Let \(I:\varOmega \subset R^3 \rightarrow R\) be a 3D image, \(\mathbf {c}=(c_x,c_y,c_z)\in R^3\), and \(\alpha ,\beta \in R\). We define the 2D image \(I_{\mathbf {c}}^{\alpha ,\beta }(x,y)\) as

$$\begin{aligned} I_{\mathbf {c}}^{\alpha ,\beta }(x,y)=I\left( \left( \begin{array} [c]{c} c_{x}\\ c_{y}\\ c_{z} \end{array} \right) +\left( \begin{array} [c]{ccc} \cos \alpha &{} 0 &{} \sin \alpha \\ -\sin \alpha \sin \beta &{} \cos \beta &{} \cos \alpha \sin \beta \\ -\cos \beta \sin \alpha &{} -\sin \beta &{} \cos \alpha \cos \beta \end{array} \right) \left( \begin{array} [c]{c} x\\ y\\ 0 \end{array} \right) \right) . \end{aligned}$$
(2)

\(I_{\mathbf {c}}^{\alpha ,\beta }(x,y)\) corresponds to the intersection of the 3D image I with the plane that contains the point \(\mathbf {c}\) and is orthogonal to \(\mathbf {u}=\left( \sin \alpha ,\cos \alpha \sin \beta ,\cos \alpha \cos \beta \right) \). For each \(\alpha ,\beta \), we denote by \(C_{\mathbf {c,}\sigma }^{\alpha ,\beta }\) the ellipse which optimizes energy \(E_1\) for the image \(I_{\mathbf {c}}^{\alpha ,\beta }(x,y)\). That is

$$\begin{aligned} C_{\mathbf {c,}\sigma }^{\alpha ,\beta }=\underset{C}{\underbrace{\arg \min }} E_{1}(C,I_{\mathbf {c}}^{\alpha ,\beta },\sigma ). \end{aligned}$$
(3)

Next, to estimate the best orientation of the cross-sectional plane, given by the angles \(\alpha \) and \(\beta \), we introduce the following new energy:

$$\begin{aligned} E(\alpha ,\beta ,\mathbf {c})=w_{1}E_{1}(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })+w_{2} \underset{E_{2}(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })}{\underbrace{\sqrt{Area(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })}}}+w_{3}\underset{E_{3} (C_{\mathbf {c,}\sigma }^{\alpha ,\beta } )}{\underbrace{Eccentricity(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })}}, \end{aligned}$$
(4)

where \(w_1,w_2,w_3\ge 0\). The above energy \(E(\alpha ,\beta ,\mathbf {c})\) is the balance of 3 terms: \(E_1(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })\), which measures the quality of the ellipse in the sense that it fits a high-contrast contour, \(E_2(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })\), which penalizes the fact that the ellipse has a large area, and \(E_3(C_{\mathbf {c,}\sigma }^{\alpha ,\beta })\), which penalizes that the ellipse shape is far from a circle. Roughly speaking, by minimizing energy \(E(\alpha ,\beta )\), we look for a cross-sectional plane where the associated ellipse fits a high contrast area, is as small (in area) as possible, and is as close to a circle as possible.

In order to set proper values for the weight parameters \(w_i\), we seek to balance the three terms of the energy. It must be noted that, in the CT images, \(E_1\) is proportional to intensity values of the image, close to several hundreds. \(E_2\) (square root of the area of the ellipse which fits the aorta cross-section) is a few tens of units approximately, and \(E_3\) (eccentricity) is in the range [0, 1). Because of that, in all the experiments performed, the following values have been used: \(w_1=0.1\), \(w_2=1\) and \(w_3=10\).

The method we propose to track the centerline, the cross-sectional planes and the ellipses can be divided into the following steps:

  1. 1.

    We perform a basic preprocessing of the 3D image I using 2 thresholds \(T_2>T_1\) by updating I in the following way

    $$\begin{aligned} I(x,y,z)=\left\{ \begin{array} [c]{ccl} I(x,y,z) &{} \text {if} &{}\quad I(x,y,z)\in [T_{1},T_{2}]\\ T_{1} &{} \text {if} &{}\quad I(x,y,z)<T_1\\ T_{2} &{} \text {if} &{}\quad I(x,y,z)>T_2 \end{array} \right. \end{aligned}$$
    (5)

    The interval \([T_1,T_2]\) corresponds to a broad range of image intensities that include both the lumen and its surrounding area. In practice, the interval \([T_1,T_2]\) is selected based on the HU (Hounsfield Units) of the original image, to exclude, in the vicinity of the aorta, dark areas due to the presence of air or bright spots due to calcifications.

  2. 2.

    We manually select a seed point inside the aortic lumen and a direction to track the aortic lumen geometry upward or downward. We can choose any slice where the aorta has an elliptical shape in the axial view. A slice at the level of the carina is a good reference to perform this task [10].

  3. 3.

    We compute the ellipse in the slice of the 3D image which contains the seed point using the technique proposed in [1]. As initial guess to obtain the ellipse, we use a circle of radius 10 pixels centered at the seed point. Given the usual size of the aorta in a CT image, this initial circle size is not too far from the actual ellipse location and the technique proposed in [1] is able to compute properly the ellipse from this initial circle. The center of the obtained ellipse will be the first centerline point \(\mathbf {c}^0\). From this ellipse, (using [1]) we compute the initial orientation \((\alpha _0,\beta _0)\) of the cross-sectional plane which passes through \(\mathbf {c}^0\) and whose orthogonal direction is given by

    $$\begin{aligned} \mathbf {u}_0=\pm \left( \sin \alpha _0,\cos \alpha _0 \sin \beta _0,\cos \alpha _0\cos \beta _0\right) . \end{aligned}$$
    (6)

    The sign of \(\mathbf {u}_0\) is initially fixed according to the initial choice of the tracking direction (upward or downward).

  4. 4.

    We start the following iterative procedure to track the centerline point \(\mathbf {c}^n\), the orientation of the cross-sectional plane \((\alpha _n,\beta _n)\) and the ellipse in each cross-section \(C_{\mathbf {c}^n,\sigma }^{\alpha _n,\beta _n}\).

    1. (a)

      We compute an initial estimation of \(\mathbf {c}^n\) as

      $$ \mathbf {c}^n= \mathbf {c}^{n-1}+h\cdot \mathbf {u}_{n-1}, $$

      where h is a discretization step (in the experiments we use \(h=1\))

    2. (b)

      We compute \(({\alpha _n,\beta _n})\) and \(C_{\mathbf {c}^n,\sigma }^{\alpha _n,\beta _n}\) by minimizing energy \(E(\alpha ,\beta ,\mathbf {c}^n)\) with respect to \(\alpha ,\beta \), that is

      $$\begin{aligned} (\alpha _n,\beta _n)=\underset{\alpha ,\beta }{\underbrace{\arg \min }}E(\alpha ,\beta ,\mathbf {c}^n). \end{aligned}$$
      (7)

      The minimization is performed by a Newton-Raphson-type algorithm using the previous values \(({\alpha _{n-1},\beta _{n-1}})\) as initial guess for \(({\alpha _n,\beta _n})\).

    3. (c)

      We update \(\mathbf {c}^n\) by applying the isometry defined in (2) to the center of the ellipse \(C_{\mathbf {c}^n,\sigma }^{\alpha _n,\beta _n}\).

    4. (d)

      We compute the orthogonal direction \(\mathbf {u}_n\) to the cross-sectional plane as

      $$\begin{aligned} \mathbf {u}_n=\pm \left( \sin \alpha _n,\cos \alpha _n \sin \beta _n,\cos \alpha _n\cos \beta _n\right) , \end{aligned}$$
      (8)

      where the sign of \(\mathbf {u}_n\) is fixed in such a way that \(\mathbf {u}_n \cdot \mathbf {u}_{n-1}>0\).

3 Experimental Results

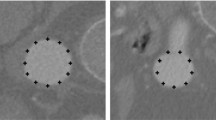
First we present an experiment using an aorta phantom built from a glass tube with a mixture of water and a radiographic contrast media inside, introduced in a CT scanner. The image size is \(512\times 512\times 273\) and the voxel size is \(0.703\times 0.703\times 0.620\,\mathrm{{mm}}^3\). Figure 1 shows the original phantom, a slice of the CT image of the phantom, a zoom of the first selected slice with the initial circle (white dots) and the first ellipse obtained using the proposed method (black dots), and a 3D representation of the whole set of computed ellipses depicted on each cross-sectional plane. In the video sequences CT_Phantom_Original.gif, CT_Phantom_Cross_Sections.gif (all videos presented are available as supplementary material), we show the CT image of the phantom, and an image built using all the cross-sections obtained using the proposed method. The external diameter of the phantom has been manually measured with a caliper in 292 different locations of the phantom structure and, in Table 1 we present a comparison of these diameter measurements with the ones obtained using the ellipses we compute in the aortic cross-sectional planes (we obtain 607 aorta cross-sections along the aortic lumen). We can observe that the results are very accurate, obtaining an average error for the minimum diameter of only 0.02 mm.

Fig. 1.
figure 1

From left to right: (a) the original phantom, (b) a slice of the CT image of the phantom, (c) zoom of the first selected slice including the initial circle (white dots) and the obtained ellipse (black dots), (d) 3D representation of the ellipses obtained in the aortic lumen cross-sections using the proposed method.

Full size image
Table 1. Comparison of the ellipse maximum and minimum diameters (given by the length of the major and minor axes of the ellipse) of the real phantom using a caliper and the ones obtained using the proposed method on the CT image of the phantom. N represents the number of samples to estimate the average diameters \(\overline{d_{\max }}\), \(\overline{d_{\min }}\) and their corresponding standard deviations \(\sigma (d_{\max })\), \(\sigma (d_{\min })\).
Full size table

Next we present an experiment using a CT image of a patient suffering from severe aortic elongations. The image size is \(512\times 512\times 600\) with a voxel size of \(0.703\times 0.703\times 0.620\,\mathrm{{mm}}^3\). This case is challenging because the aorta elongations cause angulations with high curvature foldings where the aorta shape deviates from its usual tubular structure. In Fig. 3a we show a 3D reconstruction of the aortic lumen computed and validated manually by a radiologist where we can observe such elongations. In the video CT_Aorta_Elongation_Original.gif we show the original CT image. In Fig. 2 we show some cross-sections obtained using the proposed method. We can observe that, due to the aorta angulations the ellipses in the cross-sections are sometimes far from a circular shape. In the video CT_Aorta_Elongation_Cross_Sections.gif, we show an image built using all the obtained cross-sections of the aortic lumen. In Fig. 3 we compare visually the segmentation obtained by the radiologist and the 3D representation of the ellipses we obtain in each aortic lumen cross-section. To compare the segmentation provided by the radiologist and the collection of 3D ellipses we obtain in a more quantitative way, we compute, for each ellipse, the average distance from the points on the ellipse contour to the set of contour points of the segmentation obtained by the radiologist. In Table 2 we show some basic statistics of such average distance. The results are quite accurate, which means that the ellipse contour points are close to the aorta contours obtained by the radiologist. We observe that the contour discretization introduces some error in the distance estimation between both sets because the contour obtained by the radiologist is given in integer voxel precision and the ellipse contour is given in floating aritmetic precision. On the other hand, when the aorta has ramifications, the ellipse points in such areas do not correspond to points on the contour of the aorta segmentation and this introduces errors in the average distance estimation.

Fig. 2.
figure 2

Cross-sections and ellipses (black dots) obtained using the proposed method for the CT image of a patient suffering from severe elongations. In the first image we also highlight (white dots) the circle used as initial approximation of the ellipse.

Full size image
Fig. 3.
figure 3

From left to right: (a) 3D reconstruction of the aortic lumen computed and validated manually by a radiologist, (b) 3D representation of the ellipses obtained in the aortic lumen cross-sections using the proposed method.

Full size image
Table 2. Basic statistics of the average distance (in mm) from the ellipse contour points in 3D to the contours of the 3D image segmentation obtained by a radiologist. \(N=730\) represents the number of ellipses used to compute the statistics. We use as statistics, the min value, the first quartile \(Q_1\), the median, the mean, the standard deviation \(\sigma \), the third quartile \(Q_3\) and the max value of the distances.
Full size table

Computational Cost

One important advantage of the proposed technique is that it works directly on the original image and no 3D image segmentation is required. The method works locally from the initial seed point in an incremental way and the tracking procedure produces results from the very beginning. For the experiment of the real CT image shown above, the average time computation (in an INTEL(R) Core(TM) i5-3210M CPU @ 2.50 GHz) for each cross-section is only 1.37 s. Moreover, there is a large room to speed up the algorithm using parallelization techniques, so that the proposed technique is able to attain real-time constraints.

4 Conclusions

In this paper we propose a fast incremental technique for tracking the shape of the aortic lumen in CT angiography images. The method uses a robust ellipse tracking technique and an energy minimization strategy to compute the orientation of the cross-sectional planes of the aortic lumen. The method does not require global 3D image pre-segmentation and works directly on the original image in a local way. The results of the experiments performed show that the proposed method is very accurate and can cope with challenging CT cases. In particular, the procedure has been successfully applied in the presence of large angulations, such as those arising due to the existence of severe elongations of the aorta. Another remarkable conclusion is that our approach can automatically provide morphological measures of the aorta, such as the diameter and length, that can be useful in the diagnosis and follow-up of aortic diseases.