Indifferentiability of Iterated Even-Mansour Ciphers with Non-idealized Key-Schedules: Five Rounds Are Necessary and Sufficient

Abstract

We prove that the 5-round iterated Even-Mansour (IEM) construction with a non-idealized key-schedule (such as the trivial key-schedule, where all round keys are equal) is indifferentiable from an ideal cipher. In a separate result, we also prove that five rounds are necessary by describing an attack against the corresponding 4-round construction. This closes the gap regarding the exact number of rounds for which the IEM construction with a non-idealized key-schedule is indifferentiable from an ideal cipher, which was previously only known to lie between four and twelve. Moreover, the security bound we achieve is comparable to (in fact, slightly better than) the previously established 12-round bound.

1 Introduction

Background. A large number of block ciphers are so-called key-alternating ciphers. Such block ciphers alternatively apply two types of transformations to the current state: the addition (usually bitwise) of a secret key and the application of a public permutation. In more detail, an r-round key-alternating cipher with message space $\{0,1\}^n$ is a transformation of the form

$$\begin{aligned} y=k_r\oplus P_r(k_{r-1}\oplus P_{r-1}(\cdots P_2(k_1\oplus P_1(k_0\oplus x))\cdots )), \end{aligned}$$

(1)

where $(k_0, \ldots , k_r)$ are n-bit round keys (usually derived from a master key k of size close to n), where $P_1, \ldots , P_r$ are fixed, key-independent permutations and where x and y are the plaintext and ciphertext, respectively. In particular, virtually all¹ SPNs (Substitution-Permutation Networks) have this form, including, e.g., the AES family.

A recent trend has been to analyze this class of block ciphers in the so-called Random Permutation Model (RPM), which models the permutations $P_1,\ldots ,P_r$ as oracles that the adversary can only query (from both sides) in a black-box way, each behaving as a perfectly random permutation. This approach allows to assert the nonexistence of generic attacks, i.e., attacks not exploiting the particular structure of “concrete” permutations endowed with short descriptions. This approach dates back to Even and Mansour [25] who studied the case $r=1$. For this reason, construction (1), once seen as a way to define a block cipher from an arbitrary tuple of permutations $\mathbf {P}=(P_1,\ldots ,P_r)$, is often called the iterated Even-Mansour (IEM) construction. The general case of $r\ge 2$ rounds was only considered more than 20 years later in a series of papers [11,12,13, 31, 37, 45], primarily focusing on the standard security notion for block ciphers, namely pseudorandomness, which requires that no computationally bounded adversary with (usually two-sided) black-box access to a permutation can distinguish whether it is interacting with the block cipher under a random key or a perfectly random permutation. Pseudorandomness of the IEM construction with independent round keys is by now well understood, the security bound increasing beyond the “birthday bound” (the original bound proved for the 1-round Even-Mansour construction [24, 25]) as the number of rounds increases [13, 31].

The Ideal Cipher Model. Although pseudorandomness has been the primary security requirement for a block cipher, in some cases this property is not enough to establish the security of higher-level cryptosystems using the block cipher. For example, the security of some real-world authenticated encryption protocols such as 3GPP confidentiality and integrity protocols f8 and f9 [33] rely on the stronger block cipher security notion of indistinguishability under related-key attacks [3, 7]. Problems also arise in the context of block-cipher based hash functions [36, 42] where the adversary can control both the message and the key of the block cipher, and hence can exploit “known-key” or “chosen-key” attacks [8, 35] in order to break the collision- or preimage-resistance of the hash function.

Hence, cryptographers have come to view a good block cipher as something close to an ideal cipher (IC), i.e., a family of $2^{\kappa }$ uniformly random and independent permutations, where $\kappa$ is the key-length of the block cipher. Perhaps not surprisingly, this view turned out to be very fruitful for proving the security of constructions based on a block cipher when the PRP assumption is not enough [4, 6, 10, 22, 28, 34, 41, 46], an approach often called the ideal cipher model (ICM). This ultimately remains a heuristic approach, as one can construct (artificial) schemes that are secure in the ICM but insecure for any concrete instantiation of the block cipher, similarly to the random oracle model [5, 9, 27]. On the other hand, a proof in the ideal cipher model is typically considered a good indication of security from the point of view of practice.

Indifferentiability. While an IC remains unachievable in the standard model for reasons stated above (and which boil down to basic considerations on the amount of entropy in the system), it remains an interesting problem to “build” ICs (secure in some provable sense) from other ideal primitives. This is precisely the approach taken by the indifferentiability framework, introduced by Maurer et al. [40] and popularized by Coron et al. [17]. Indifferentiability is a simulation-based framework that helps assess whether a construction of a target primitive A (e.g., a block cipher) from a lower-level ideal primitive B (e.g., for the IEM construction, a small number of random permutations $P_1,\ldots ,P_r$) is “structurally close” to the ideal version of A (e.g., an IC). Indifferentiability comes equipped with a composition theorem [40] which implies that a large class of protocols (see [21, 43] for restrictions) are provably secure in the ideal-B model if and only if they are provably secure in the ideal-A model.

We note that indifferentiability does not presuppose the presence of a private key; indeed, a number of indifferentiability proofs concern the construction of a keyless primitive (such as a hash function, compression function or permutation) from a lower-level primitive [1, 17, 32]. In the case of a block cipher, thus, the key is “just another input” to the construction.

Previous Results. Two papers have previously explored the indifferentiability of the IEM construction from an ideal cipher, modeling the underlying permutations as random permutations. Andreeva et al. [1] showed that the 5-round IEM construction with an idealized key-schedule (i.e., the function(s) mapping the master key onto the round key(s) are modeled as random oracles) is indifferentiable from an IC. Lampe and Seurin [38] showed that the 12-round IEM construction with the trivial key-schedule, i.e., in which all round keys are equal, is also indifferentiable from an IC. Moreover, both papers included impossibility results for the indifferentiability of the 3-round IEM construction with a trivial key-schedule, showing that at least four rounds must be necessary in that context. In both settings, the question of the exact number of rounds needed to make the IEM construction indifferentiable from an ideal cipher remained open.

Our Results. We improve both the positive and negative results for the indifferentiability of the IEM construction with the trivial (and more generally, non-idealized) key-schedule. Specifically, we show an attack on the 4-round IEM construction, and prove that the 5-round IEM construction is indifferentiable from an IC, in both cases for the trivial key-schedule.² Hence, our work resolves the question of the exact number of rounds needed for the IEM construction with a non-idealized key-schedule to achieve indifferentiability from an IC.

Our 4-round impossibility result improves on the afore-mentioned 3-round impossibility results [1, 38]. It can be seen as an extension of the attack against the 3-round IEM with the trivial key-schedule [38]. However, unlike this 3-round attack, our 4-round attack does not merely consist in finding a tuple of key/plaintext/ciphertext triples for the construction satisfying a so-called “evasive” relation (i.e., a relation which is hard to find with only black-box access to an ideal cipher, e.g., a triple (k, x, y) such that $x\oplus y=0$). Instead, it relies on relations on the “internal” variables of the construction (which makes the attack harder to analyze rigorously). We note that a simple “evasive-relation-finding” attack against four rounds had previously been excluded by Cogliati and Seurin [14] (in technical terms, they proved that the 4-round IEM construction is sequentially-indifferentiable from an IC, see the remark after Theorem 1 in Sect. 3) so the extra complexity of our 4-round attack is in a sense inevitable.

Our 5-round feasibility result can be seen as improving both the 5-round result for the IEM construction with idealized key-schedules [1] (albeit see the fine-grained metrics below) and on the 12-round feasibility result for the IEM construction with the trivial key-schedule [38]. Our simulator runs in time $O(q^5)$, makes $O(q^5)$ IC queries, and achieves security $2^{41}\cdot q^{12}/2^n$, where q is the number of distinguisher queries. By comparison, these metrics are respectively

$$ O(q^3),\,\, O(q^2),\,\, 2^{34} \cdot q^{10}/2^n $$

for the 5-round simulator of Andreeva et al. [1] with idealized key-schedule, and

$$ O(q^4),\,\, O(q^4),\,\, 2^{91}\cdot q^{12}/2^n $$

for the 12-round simulator of Lampe and Seurin [38]. Hence, as far as the security bound is concerned at least, we achieve a slight improvement over the previous (most directly comparable) work.

A Glimpse at the Simulator. Our 5-round simulator follows the traditional “chain detection/completion” paradigm, pioneered by Coron et al. [16, 18, 32] for proving indifferentiability of the Feistel construction, which has since been used for the IEM construction as well [1, 38]. However, it is, in a sense, conceptually simpler and more “systematic” than previous simulators for the IEM construction (something we pay for by a more complex “termination” proof). In a nutshell, our new 5-round simulator detects and completes any path of length 3, where a path is a sequence of adjacent permutation queries “chained” by the same key (and which might “wrap around” the ideal cipher). In contrast, the 12-round simulator of [38] used a much more parsimonious chain detection strategy (inherited from [16, 18, 32, 44]) which allowed a much simpler termination argument.

Once a tentative simulator has been determined, the indifferentiability proof usually entails two technical challenges: on the one hand, proving that the simulator works hard enough to ensure that it will never be trapped in an inconsistency, and on the other hand, proving that it does not work in more than polynomial time. Finding the right balance between these two requirements is at the heart of the design of a suitable simulator.

The proof that our new 5-round simulator remains consistent with the IC roughly follows the same ideas as in previous indifferentiability proofs. In short, since the simulator completes all paths of length 3, at the moment the distinguisher makes a permutation query, only incomplete paths of length at most two can exist. Hence any incomplete path has three “free” adjacent positions, two of which (the ones on the edge) will be sampled at random, while the middle one will be adapted to match the IC. The most delicate part consists in proving that no path of length 3 can appear “unexpectedly” and remain unnoticed by the simulator (which will therefore not complete it), except with negligible probability.

The more innovative part of our proof lies in the “termination argument”, i.e., in proving that the simulator is efficient and that the recursive chain detection/completion process does not “chain react” beyond a fixed polynomial bound. As in many previous termination arguments [16, 18, 23, 32, 44], we first observe that certain types of paths (namely those that wrap around the IC) are only ever detected and completed if the distinguisher made the corresponding IC query. Hence, assuming the distinguisher makes at most q queries, at most q such paths will be triggered and completed. In virtually all previous indifferentiability proofs, this fact easily allows to upper bound the size of permutation histories for all other “detect zones” used by the simulator, and hence to upper bound the total number of paths that will ever be detected and completed. (Indeed, all of the indifferentiability results in the afore-mentioned list actually have quite simple termination arguments!) But in the case of our 5-round simulator, this observation only allows us to upper bound the size of the middle permutation $P_3$, which by itself is not sufficient to upper bound the number of other detected paths. To push the argument further, we make some additional observations—essentially, that every triggered path that is not a “wraparound” path associated to some distinguisher query is uniquely (i.e., injectively) associated to one of: (i) a pair of $P_3$ and $P_1$ entries, where the $P_1$ entry was directly queried by the distinguisher, or (ii) symmetrically, a pair of $P_3$ and $P_5$ entries, where the $P_5$ entry was directly queried by the distinguisher, or (iii) a pair of $P_3$ entries. (In some sense, the crucial “trick” that allows to fall back on (iii) in all other cases is the observation that every query that is left over from a previous query cycle and that is not the direct result of a distinguisher query is in a completed path, and this completed path contains a query at $P_3$.) This suffices, because the distinguisher makes only q queries and because of the afore-mentioned bound on the size of $P_3$. In order to show that the association described above is truly injective, a structural property of $P_2$ and $P_4$ is needed, namely that the table maintaining answers of the simulator for $P_2$ (resp. $P_4$) never contains 4 distinct input/output pairs $(x^{(i)},y^{(i)})$, such that $\bigoplus _{1\le i\le 4}(x^{(i)}\oplus y^{(i)})=0$. Since some queries are “adapted” to fit the IC, proving this part ends up being a source of some tedium as well.

Related Work. Several papers have studied security properties of the IEM construction that are stronger than pseudorandomness yet weaker than indifferentiability, such as resistance to related-key [14, 26], known-key [2, 15], or chosen-key attacks [14, 29]. A recent preprint shows that the 3-round IEM construction with a (non-invertible) idealized key-schedule is indifferentiable from an IC [30]. This complements our work by settling the problem analogous to ours in the case of idealized key-schedules. In both cases, the main open question is whether the concrete indifferentiability bounds (which are typically poor) can be improved.

Organization. Preliminary definitions are given in Sect. 2. The attack against the 4-round IEM construction is given in Sect. 3. Our 5-round simulator is described in Sect. 4, while the indifferentiability proof is in Sect. 5.

2 Preliminaries

Throughout the paper, n will denote the block length of permutations $P_1,\ldots ,P_r$ of the IEM construction and will play the role of security parameter for asymptotic statements. Given a finite non-empty set S, we write $s\leftarrow _{\$}S$ to mean that an element is drawn uniformly at random from S and assigned to s.

A distinguisher is an oracle algorithm $\mathcal {D}$ with oracle access to a finite list of oracles $(\mathcal {O}_1,\mathcal {O}_2,\ldots )$ and that outputs a single bit b, which we denote $\mathcal {D}^{\mathcal {O}_1,\mathcal {O}_2,\ldots }=b$ or $\mathcal {D}[\mathcal {O}_1,\mathcal {O}_2,\ldots ]=b$.

A block cipher with key space $\{0,1\}^\kappa$ and message space $\{0,1\}^n$ is a mapping $E:\{0,1\}^\kappa \times \{0,1\}^n\rightarrow \{0,1\}^n$ such that for any key $k\in \{0,1\}^\kappa$, $x\mapsto E(k,x)$ is a permutation. An ideal cipher with block length n and key length $\kappa$ is a block cipher drawn uniformly at random from the set of all block ciphers with block length n and key length $\kappa$.

The IEM Construction. Fix integers $n,r\ge 1$. Let $\mathbf {f}=(f_0,\ldots ,f_r)$ be a $(r+1)$-tuple of functions from $\{0,1\}^n$ to $\{0,1\}^n$. The r-round iterated Even-Mansour construction $\mathrm {EM}[n,r,\mathbf {f}]$ specifies, from any r-tuple $\mathbf {P}=(P_1,\ldots ,P_r)$ of permutations of $\{0,1\}^n$, a block cipher with n-bit keys and n-bit messages, simply denoted $\mathrm {EM}^{\mathbf {P}}$ in all the following (parameters $[n,r,\mathbf {f}]$ will always be clear from the context), which maps a plaintext $x\in \{0,1\}^n$ and a key $k\in \{0,1\}^n$ to the ciphertext defined by

$$ \mathrm {EM}^{\mathbf {P}}(k,x)=f_r(k)\oplus P_r(f_{r-1}(k)\oplus P_{r-1}(\cdots P_2(f_1(k)\oplus P_1(f_0(k)\oplus x))\cdots )). $$

We say that the key-schedule is trivial when all $f_i$’s are the identity.

Note that the first and last key additions do not play any role for indifferentiability where the key is just a “public” input to the construction, much like the plaintext/ciphertext. What provides security are the random permutations, that remain secret for inputs that have not been queried by the attacker. So, we will focus on a slight variant of the trivial key-schedule where $f_0=f_r=0$ (see Fig. 1), but our results carry over to the trivial key-schedule (and more generally to any non-idealized key-schedule where the $f_i$’s are permutations on $\{0,1\}^n$).

Fig. 1.

The 5-round iterated Even-Mansour construction with independent permutations and identical round keys. The first and last round key additions are omitted since they do not play any role for the indifferentiability property.

Indifferentiability. We recall the standard definition of indifferentiability for the IEM construction.

Definition 1

The construction $\mathrm {EM}^{\mathbf P}$ with access to an r-tuple $\mathbf {P}= (P_1,\ldots ,P_r)$ of random permutations is $(t_\mathcal {S},q_\mathcal {S},\varepsilon )$ -indifferentiable from an ideal cipher $\mathrm {IC}$ if there exists a simulator $\mathcal {S}= \mathcal {S}(q)$ such that $\mathcal {S}$ runs in total time $t_\mathcal {S}$ and makes at most $q_\mathcal {S}$ queries to $\mathrm {IC}$, and such that

$$ \big | \Pr [D^{\mathrm {EM}^{\mathbf {P}}, \mathbf {P}} = 1] - \Pr [D^{\mathrm {IC}, \mathcal {S}^{\mathrm {IC}}} = 1] \big | \le \varepsilon $$

for every (information-theoretic) distinguisher D making at most q queries in total.

We say that the r-round IEM construction is indifferentiable from an ideal cipher if for any q polynomial in n, it is $(t_\mathcal {S},q_\mathcal {S},\varepsilon )$-indifferentiable from an ideal cipher with $t_\mathcal {S},q_\mathcal {S}$ polynomial in n and $\varepsilon$ negligible in n.

Remark 1

Definition 1 allows the simulator $\mathcal {S}$ to depend on the number of queries q. In fact, our simulator (cf. Figs. 4 and 5) does not depend on q, but is efficient only with high probability. In the full version of the paper [19], we discuss an optimized implementation of our simulator that, among others, uses knowledge of q to abort whenever its runtime exceeds the limit of a “good” execution, thus ensuring that it is efficient with probability 1.

3 Attack Against 4-Round Simulators

We describe an attack against the 4-round IEM construction, improving previous attacks against 3 rounds [1, 38]. Consider the distinguisher $\mathcal {D}$ whose pseudocode is given in Fig. 2 (see also Fig. 3 for an illustration of the attack). This distinguisher can query the permutations/simulator through the interface $\mathrm {Query}(i,\delta ,z)$, and the EM construction/ideal cipher through interfaces $\mathrm {Enc}(k,x)$ and $\mathrm {Dec}(k,y)$.

Fig. 2.

Pseudocode of the attack against the 4-round IEM construction.

Fig. 3.

Illustration of the attack against the 4-round IEM construction. The circled dots correspond to queries made by the distinguisher to the permutations/simulator.

We prove that $\mathcal {D}$ has advantage close to 1 / 2 against any simulator making a polynomial number of queries to the IC. More formally, we have the following result, whose proof can be found in the full version of the paper [19]:

Theorem 1

Let $\mathcal {S}$ be any simulator making at most $\sigma$ IC queries when interacting with $\mathcal {D}$. Then the advantage of $\mathcal {D}$ in distinguishing $(\mathrm {EM}^{\mathbf {P}},\mathbf {P})$ and $(\mathrm {IC},\mathcal {S}^{\mathrm {IC}})$ is at least

$$ \frac{1}{2} - \frac{4\sigma }{2^n} - \frac{7}{2^n}. $$

As an additional remark, say that a distinguisher is sequential [14, 39] if it first queries only its right interface (random permutations/simulator), and then only its left interface (IEM construction/ideal cipher), but not its right interface anymore. Many “natural” attacks against indifferentiability are sequential (in particular, the attack against 5-round Feistel of [18] and the attack against 3-round IEM of [38]), running in two phases: first, the distinguisher looks for input/output pairs satisfying some relation which is hard to satisfy for an ideal cipher (a so-called “evasive” relation) by querying the right interface; then, it checks consistency of these input/output pairs by querying the left interface (since the relation is hard to satisfy for an ideal cipher, any polynomially-bounded simulator will fail to consistently simulate the inner permutations in the ideal world). We note that the attack described in this section is not sequential. This does not come as a surprise since Cogliati and Seurin [14] showed that the 4-round IEM construction is sequentially indifferentiable from an IC, i.e., indifferentiable from an IC by any sequential distinguisher. Hence, our new attack yields a natural separation between (full) indifferentiability and sequential indifferentiability.

4 The 5-Round Simulator

We start with a high-level overview of how the simulator $\mathcal {S}$ works, deferring the formal description in pseudocode to Sect. 4.1. For each $i\in \{1,\ldots ,5\}$, the simulator maintains a pair of tables $P_i$ and $P_i^{-1}$ with $2^n$ entries containing either an n-bit value or a special symbol $\bot$, allowing the simulator to keep track of values that have already been assigned internally for the i-th permutation. Initially, these tables are empty, meaning that $P_i(x)=P_i^{-1}(y)=\bot$ for all $x,y\in \{0,1\}^n$. The simulator sets $P_i(x)\leftarrow y$, $P_i^{-1}(y)\leftarrow x$ to indicate that the i-th permutation maps x to y. The simulator never overwrites entries in $P_i$ or $P_i^{-1}$, and always keeps these two tables consistent, so that $P_i$ always encodes a “partial permutation” of $\{0,1\}^n$. We sometimes write $x\in P_i$ (resp. $y\in P_i^{-1}$) to mean that $P_i(x)\ne \bot$ (resp. $P_i^{-1}(y)\ne \bot$).

The simulator offers a single public interface $\mathrm {Query}(i,\delta ,z)$ allowing the distinguisher to request the value $P_i(z)$ when $\delta =+$ or $P_i^{-1}(z)$ when $\delta =-$ for $z\in \{0,1\}^n$. Upon reception of a query $(i,\delta ,z)$, the simulator checks whether $P_i^\delta (z)$ has already been defined, and returns the corresponding value if this is the case. Otherwise, it marks the query $(i,\delta ,z)$ as “pending” and starts a “chain detection/completion” mechanism, called a permutation query cycle in the following, in order to maintain consistency between its answers and the IC as we now explain. (We stress that some of the wording introduced here is informal and that all notions will be made rigorous in the next sections.)

We say that a triple $(i,x_i,y_i)$ is table-defined if $P_i(x_i)=y_i$ and $P_i^{-1}(y_i)=x_i$ (that is, the simulator internally decided that $x_i$ is mapped to $y_i$ by permutation $P_i$). Let us informally call a tuple of $j-i+1\ge 2$ table-defined permutation queries at adjacent positions $((i,x_i,y_i),\ldots ,(j,x_j,y_j))$ (indices taken mod 5) such that $x_{i+1}=y_i\oplus k$ if $i\ne 5$ and $x_{i+1}=\mathrm {IC}^{-1}(k,y_i)$ if $i=5$ a “k-path of length $j+i-1$” (hence, paths might “wrap around” the IC).

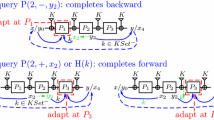
The very simple idea at the heart of the simulator is that, before answering any query of the distinguisher to some simulated permutation, it ensures that any path of length three (or more) has been preemptively extended to a “complete” path of length five $((1,x_1,y_1),\ldots ,(5,x_5,y_5))$ compatible with the ideal cipher (i.e., such that $\mathrm {IC}(k,x_1)=y_5$). For this, assume that at the moment the distinguisher makes a permutation query $(i,\delta ,z)$ which is not table-defined yet (otherwise the simulator just returns the existing answer), any path of length three is complete. This means that any existing incomplete path has length at most two. These length-2 paths will be called (table-defined³) 2chains in the main body of the proof, and will play a central role. For ease of the discussion to come, let us call the pair of adjacent positions $(i,i+1)$ of the table-defined queries constituting a 2chain the type of the 2chain. (Note that as any path, a 2chain can “wrap around”, i.e., consists of two table-defined queries $(5,x_5,y_5)$ and $(1,x_1,y_1)$ such that $\mathrm {IC}(k,x_1)=y_5$, so that possible types are (1, 2), (2, 3), (3, 4), (4, 5), and (5, 1).) Let us also call the direct input to permutation $P_{i+2}$ and the inverse input to permutation $P_{i-1}$ when extending the 2chain in the natural way the right endpoint and left endpoint of the 2chain, respectively.⁴

The “pending” permutation query $(i,\delta ,z)$ asked by the distinguisher might create new incomplete paths of length 3 (once answered by the simulator) when combined with adjacent 2chains, that is, 2chains at position $(i-2,i-1)$ for a direct query $(i,+,x_i)$ or 2chains at position $(i+1,i+2)$ for an inverse query $(i,-,y_i)$. Hence, just after having marked the initial query of the distinguisher as “pending”, the simulator immediately detects all 2chains that will form a length-3 path with this pending query, and marks these 2chains as “triggered”. Following the high-level principle of completing any length-3 path, any triggered 2chain should (by the end of the query cycle) be extended to a complete path.

To ease the discussion, let us slightly change the notation and assume that the query that initiates the query cycle is either a forward query $(i+2,+,x_{i+2})$ or an inverse query $(i-1,-,y_{i-1})$. In both cases, adjacent 2chains that might be triggered are of type $(i,i+1)$. For each such 2chain, the simulator computes the endpoint opposite the initial query, and marks it “pending” as well. Thus if the initiating query was $(i+2,+,x_{i+2})$, new pending queries of the form $(i-1,-,\cdot )$ are (possibly) created, while if the initiating query was $(i-1,-,y_{i-1})$, new pending queries of the form $(i+2,+,\cdot )$ are (possibly) created. For each of these new pending queries, the simulator recursively detects whether they form a length-3 path with other $(i,i+1)$-2chains, marks these 2chains as “triggered”, and so on. Hence, if the initiating query of the distinguisher was of the form $(i+2,+,\cdot )$ or $(i-1,-,\cdot )$, all “pending” queries will be of the form $(i+2,+,\cdot )$ or $(i-1,-,\cdot )$, and all triggered 2chains will be of type $(i,i+1)$. For this reason, we say that such a query cycle is of “type $(i,i+1)$”. Note that while this recursive process is taking place, the simulator does not assign any new values to the partial permutations $P_1, \ldots , P_5$—indeed, each pending query remains defined only “at one end” during this phase.

Once all 2chains that must eventually be completed have been detected as described above, the simulator starts the completion process. First, it randomly samples the missing endpoints of all “pending” queries. (Thus, a pending query of the form $(i+2, +, x_{i+2})$ will see a value of $y_{i+2}$ sampled; a pending query of the form $(i-1, -, y_{i-1})$ will see a value of $x_{i-1}$ sampled. The fact that each pending query really does have a missing endpoint to be sampled is argued in the proof.) Secondly, for each triggered 2chain, the simulator adapts the corresponding path by computing the corresponding input $x_{i+3}$ and output $y_{i+3}$ at position $i+3$ and “forcing” $P_{i+3}(x_{i+3})=y_{i+3}$. If an overwrite attempt occurs when trying to assign a value for some permutation, the simulator aborts. This completes the high-level description of the simulator’s behavior. The important characteristics of an $(i,i+1)$-query cycle are summarized in Table 1.

Table 1. The five types of $(i,i+1)$-query cycles of the simulator.

4.1 Pseudocode of the Simulator and Game Transitions

We now give the full pseudocode for the simulator, and by the same occasion describe the intermediate worlds that will be used in the indifferentiability proof. The distinguisher $\mathcal {D}$ has access to the public interface $\mathrm {Query}(i,\delta ,z)$, which in the ideal world is answered by the simulator, and to the ideal cipher/IEM construction interface, that we formally capture with two interfaces $\mathrm {Enc}(k,x)$ and $\mathrm {Dec}(k,y)$ for encryption and decryption respectively. We will refer to queries to any of these two interfaces as cipher queries, by opposition to permutation queries made to interface $\mathrm {Query}(\cdot ,\cdot ,\cdot )$. In the ideal world, cipher queries are answered by an ideal cipher $\mathrm {IC}$. We make the randomness of $\mathrm {IC}$ explicit through two random tapes $\mathsf {ic}$, $\mathsf {ic}^{-1}:\{0,1\}^n\times \{0,1\}^n\rightarrow \{0,1\}^n$ such that for any $k\in \{0,1\}^n$, $\mathsf {ic}(k,\cdot )$ is a uniformly random permutation and $\mathsf {ic}^{-1}(k,\cdot )$ is its inverse. Hence, in the ideal world, a query $\mathrm {Enc}(k,x)$, resp. $\mathrm {Dec}(k,y)$, is simply answered with $\mathsf {ic}(k,x)$, resp. $\mathsf {ic}^{-1}(k,y)$. The randomness used by the simulator for lazily sampling permutations $P_1,\ldots ,P_5$ when needed is also made explicit in the pseudocode through uniformly random permutations tapes $\mathbf {p}=(p_1,p_1^{-1},\ldots ,p_5,p_5^{-1})$ where $p_i:\{0,1\}^n\rightarrow \{0,1\}^n$ is a uniformly random permutation and $p_i^{-1}$ is its inverse. Hence, randomness in game $\mathsf {G}_1$ is fully captured by $\mathsf {ic}$ and $\mathbf {p}$.

Since we will use two intermediate games, the real world will be denoted $\mathsf {G}_4$. In this world, queries to $\mathrm {Query}(\cdot ,\cdot ,\cdot )$ are simply answered with the corresponding value stored in the random permutation tapes $\mathbf {p}$, while queries to $\mathrm {Enc}$ or $\mathrm {Dec}$ are answered by the IEM construction based on random permutations $\mathbf {p}$. Randomness in $\mathsf {G}_4$ is fully captured by $\mathbf {p}$.

Intermediate Games. The indifferentiability proof relies on two intermediate games $\mathsf {G}_2$ and $\mathsf {G}_3$. In game $\mathsf {G}_2$, following an approach of [32], the $\mathrm {Check}$ procedure used by the simulator (see Line 30 of Fig. 4) to detect new external chains is modified such that it does not make explicit queries to the ideal cipher; instead, it first checks to see if the entry exists in table T recording cipher queries and if not, returns false. In game $\mathsf {G}_3$, the ideal cipher is replaced with the 5-round IEM construction that uses the same random permutation tapes $\mathbf {p}$ as the simulator (and hence both the distinguisher and the simulator interact with the 5-round IEM construction instead of the IC).

Summing up, randomness is fully captured by $\mathsf {ic}$ and $\mathbf {p}$ in games $\mathsf {G}_1$ and $\mathsf {G}_2$, and by $\mathbf {p}$ in games $\mathsf {G}_3$ and $\mathsf {G}_4$ (since the ideal cipher is replaced by the IEM construction $\mathrm {EM}^{\mathbf {p}}$ when transitioning from $\mathsf {G}_2$ to $\mathsf {G}_3$).

Notes about the Pseudocode. The pseudocode for the public (i.e., accessible by the distinguisher) procedures $\mathrm {Query}$, $\mathrm {Enc}$, and $\mathrm {Dec}$ is given in Fig. 4, together with helper procedures that capture the changes from games $\mathsf {G}_1$ to $\mathsf {G}_4$. The pseudocode for procedures that are internal to the simulator is given in Fig. 5. Lines commented with “$\backslash \!\backslash \mathsf {G}_i$” apply only to game $\mathsf {G}_i$. In the pseudocode and more generally throughout this paper, the result of arithmetic on indices in $\{1,2,3,4,5\}$ is automatically wrapped into that range (e.g., $i+1 = 1$ if $i = 5$). For any table or tape $\mathcal {T}$ and $\delta \in \{+,-\}$, we let $\mathcal {T}^\delta$ be $\mathcal {T}$ if $\delta = +$ and be $\mathcal {T}^{-1}$ if $\delta = -$. Given a list L, $L\hookleftarrow x$ means that x is appended to L. If the simulator aborts (Line 86), we assume it returns a special symbol $\bot$ to the distinguisher.

Tables T and $T^{-1}$ are used to record the cipher queries that have been issued (by the distinguisher or the simulator). Note that tables $P_i$ and $P_i^{-1}$ are modified only by procedure Assign. The table entries are never overwritten, due to the check at Line 86.

Fig. 4.

Public procedures $\mathrm {Query}$, $\mathrm {Enc}$, and $\mathrm {Dec}$ for games $\mathsf {G}_1$-$\mathsf {G}_4$, and helper procedures $\mathrm {EM}$, $\mathrm {EM}^{-1}$, and $\mathrm {Check}$. This set of procedures captures all changes from game $\mathsf {G}_1$ to $\mathsf {G}_4$, namely: from game $\mathsf {G}_1$ to $\mathsf {G}_2$ only procedure $\mathrm {Check}$ is modified; from game $\mathsf {G}_2$ to $\mathsf {G}_3$, the only change is in procedures $\mathrm {Enc}$ and $\mathrm {Dec}$ where the ideal cipher is replaced by the IEM construction; and from game $\mathsf {G}_3$ to $\mathsf {G}_4$, only procedure $\mathrm {Query}$ is modified to return directly the value read in random permutation tables $\mathbf {p}$.

Fig. 5.

Private procedures used by the simulator.

5 Proof of Indifferentiability

5.1 Main Result and Proof Overview

Our main result is the following theorem which uses the simulator described in Sect. 4. We present an overview of the proof following the theorem statement.

Theorem 2

The 5-round iterated Even-Mansour construction $\mathrm{EM}^{\mathbf {P}}$ with random permutations $\mathbf {P}=(P_1,\ldots ,P_5)$ is $(t_S, q_S, \varepsilon )$-indifferentiable from an ideal cipher with $t_S = O(q^5)$, $q_S = O(q^5)$ and $\varepsilon = 2 \times 10^{12}q^{12} / 2^n$.

Moreover, the bounds hold even if the distinguisher is allowed to make q permutation queries in each position (i.e., it can call $\mathrm {Query}(i, *, *)$ q times for each $i \in \{1,2,3,4,5\}$) and make q cipher queries (i.e., $\mathrm {Enc}$ and $\mathrm {Dec}$ can be called q times in total).

Proof Structure. Our proof uses a sequence of games $\mathsf {G}_1$, $\mathsf {G}_2$, $\mathsf {G}_3$ and $\mathsf {G}_4$ as described in Sect. 4.1, with $\mathsf {G}_1$ being the simulated world and $\mathsf {G}_4$ being the real world.

Throughout the proof we will fix an arbitrary information-theoretic distinguisher $\mathcal {D}$ that can make a total of 6q queries: at most q cipher queries and at most q queries to Query$(i,\cdot ,\cdot )$ for each $i \in \{1, \ldots , 5\}$, as stipulated in Theorem 2. (Giving the distinguisher q queries at each position gives it more power while not significantly affecting the proof or the bounds, and the distinguisher’s extra power actually leads to better bounds at the final stages of the proof [20].⁵) We can assume without loss of generality that $\mathcal {D}$ is deterministic, as any distinguisher can be derandomized using the “optimal” random tape and achieve at least the same advantage.

Without loss of generality, we assume that $\mathcal {D}$ outputs 1 with higher probability in the simulated world $\mathsf {G}_1$ than in the real world $\mathsf {G}_4$. We define the advantage of $\mathcal {D}$ in distinguishing between $\mathsf {G}_i$ and $\mathsf {G}_j$ by

$$ \varDelta _\mathcal {D}(\mathsf {G}_i, \mathsf {G}_j) := \Pr _{\mathsf {G}_i}[\mathcal {D}^{\mathrm {Query},\mathrm {Enc},\mathrm {Dec}} = 1] - \Pr _{\mathsf {G}_j}[\mathcal {D}^{\mathrm {Query},\mathrm {Enc},\mathrm {Dec}} = 1]. $$

Our primary goal is to upper bound $\varDelta _\mathcal {D}(\mathsf {G}_1,\mathsf {G}_4)$ (in Theorem 20), while the secondary goals of upper bounding the simulator’s query complexity and running time will be obtained as corollaries along the way.

Our proof starts with discussions about the game $\mathsf {G}_2$, which is in some sense the “anchor point” of the first two game transitions. As usual, there are bad events that might cause the simulator to fail. We will prove that bad events are unlikely, and show properties of good executions in which bad events do not occur. The proof of efficiency of the simulator (in good executions of $\mathsf {G}_2$) is the most interesting part of this paper; the technical content is in Sect. 5.4, and a separate high-level overview of the argument is also included immediately below (see “Termination Argument”). During the proof of efficiency we also obtain upper bounds on the sizes of the tables and on the number of calls to each procedure, which will be a crucial component for the transition to $\mathsf {G}_4$ (see below).

For the $\mathsf {G}_1$-$\mathsf {G}_2$ transition (found in the full version [19]), note that the only difference between the two games is in $\mathrm {Check}$. If the simulator is efficient, the probability that the two executions diverge in a call to $\mathrm {Check}$ is negligible. Therefore, if an execution of $\mathsf {G}_2$ is good, it is identical to the $\mathsf {G}_1$-execution with the same random tapes except with negligible probability. In particular, this implies that an execution of $\mathsf {G}_1$ is efficient with high probability.

For the $\mathsf {G}_2$-$\mathsf {G}_3$ transition, we use a standard randomness mapping argument. We will map the randomness of good executions of $\mathsf {G}_2$ to the randomness of non-aborting executions of $\mathsf {G}_3$, so that the $\mathsf {G}_3$-executions with the mapped randomness are identical to the $\mathsf {G}_2$-executions with the preimage randomness. We will show that if the randomness of a $\mathsf {G}_3$-execution has a preimage, then the answers of the permutation queries output by the simulator must be compatible with the random permutation tapes. Thus the $\mathsf {G}_3$-execution is identical to the $\mathsf {G}_4$-execution with the same random tapes, where the permutation queries are answered by the corresponding entries of the random tapes. This enables a transition directly from $\mathsf {G}_2$ to $\mathsf {G}_4$ using the randomness mapping, which is a small novelty of our proof. The details of this transition can be found in the full version [19].

Termination Argument. Since the termination argument—i.e., the fact that our simulator does not run amok with excessive path completions, except with negligible probability—is one of the more novel aspects of our proof, we provide a separate high-level overview of this argument here.

To start with, observe that at the moment when an $(i, i+1)$-path is triggered, 3 queries on the path are either already in existence or already scheduled for future existence regardless of this event: the queries at position i and $i+1$ are already defined, while the pending query that triggers the path was already scheduled to become defined even before the path was triggered; hence, each triggered path only “accounts” for 2 new queries, positioned either at $i+2$, $i+3$ or at $i-1$, $i-2\,\, (= i + 3)$, depending on the position of the pending query.

A second observation is that...

• (1, 2)-2chains triggered by pending queries of the form $(5, -, \cdot )$, and

• (4, 5)-2chains triggered by pending queries of the form $(1, +, \cdot )$, and

• (5, 1)-2chains triggered by either pending queries of the form $(2, +, \cdot )$ or $(4, -, \cdot )$

...all involve a cipher query (equivalently, a call to Check, in $\mathsf {G}_2$) to check the trigger condition, and one can argue that this query must have been made by the distinguisher itself. (Because when the simulator makes a query to Enc/Dec that is not for the purpose of detecting paths, it is for the purpose of completing a path.) Hence, because the distinguisher only has q cipher queries, only q such path completions should occur in total. Moreover, these three types of path completions are exactly those that “account” for a new (previously unscheduled) query to be created at $P_3$. Hence, and because the only source of new queries are path completions and queries coming directly from the distinguisher, the size of $P_3$ never grows more than $q + q = 2q$, with high probability.

Of the remaining types of 2chain completions (i.e., those that do not involve the presence of a previously made “wraparound” cipher query), those that contribute a new entry to $P_2$ are the following:

• (3, 4)-2chains triggered by pending queries of the form $(5, +, \cdot )$

• (4, 5)-2chains triggered by pending queries of the form $(3, -, \cdot )$

We can observe that either type of chain completion involves values $y_3$, $x_4$, $y_4$, $x_5$ that are well-defined at the time the chain is detected. We will analyze both types of path completion simultaneously, but dividing into two cases according to whether (a) the distinguisher ever made the query Query$(5, +, x_5)$, or else received the value $x_5$ as an answer to a query of the form Query$(5, -, y_5)$, or (b) the query $P_5(x_5)$ is being defined/is already defined as the result of a path completion. (Crucially, (a) and (b) are the only two options for $x_5$.)

For (a), at most q such values of $x_5$ can ever exist, since the distinguisher makes at most q queries to Query$(5, \cdot , \cdot )$; moreover, there are at most 2q possibilities for $y_3$, as already noted; and we have the relation

$$\begin{aligned} y_3 \oplus x_5 = x_4 \oplus y_4 \end{aligned}$$

(2)

from the fact that $y_3$, $x_4$, $y_4$ and $x_5$ lie on a common path. One can show that, with high probability,

$$ x_4 \oplus y_4 \ne x_4' \oplus y_4' $$

for all $x_4$, $y_4$, $x_4'$, $y_4'$ such that $P_4(x_4) = y_4$, $P_4(x_4') = y_4'$ and such that $x_4 \ne x_4'$.⁶ Hence, with high probability (2) has at most a unique solution $x_4$, $y_4$ for each $y_3$, $x_5$, and scenario (a) accounts for at most $2q^2$ path completions (one for each possible left-hand side of (2)) of either type above.

For (b), there must exist a separate (table-defined) 2chain $(3, x_3', y_3')$, $(4, x_4', y_4')$ whose right endpoint is $x_5$. (This is the case if $x_5$ is part of a previously completed path, and is also the case if $(5, +, x_5)$ became a pending query during the current query cycle without being the initiating query.) The relation

$$ y_3' \oplus x_4' \oplus y_4' = y_3 \oplus x_4 \oplus y_4 $$

(both sides are equal to $x_5$) implies

$$\begin{aligned} y_3 \oplus y_3' = x_4 \oplus y_4 \oplus x_4' \oplus y_4' \end{aligned}$$

(3)

and, similarly to (a), one can show that (with high probability)

$$ x_4 \oplus y_4 \oplus x_4' \oplus y_4' \ne X_4 \oplus Y_4 \oplus X_4' \oplus Y_4' $$

for all table-defined queries $(4, x_4, y_4), \ldots , (4, X_4', Y_4')$ with $\{(x_4, y_4), (x_4', y_4')\} \ne \{(X_4, Y_4), (X_4', Y_4')\}$. Thus, we have (modulo the ordering of $(x_4, y_4)$ and $(x_4', y_4')$ ⁷) at most one solution to the RHS of (3) for each LHS; hence, scenario (b) accounts for at most $4q^2$ path completions⁸ of either type above, with high probability.

Combining these bounds, we find that $P_2$ never grows to size more than $2q + 2q^2 + 4q^2 = 6q^2 + 2q$ with high probability, where the term of 2q accounts for (the sum of) direct distinguisher queries to Query$(2,\cdot ,\cdot )$ and “wraparound” path completions involving a distinguisher cipher query. Symmetrically, one can show that $P_4$ also has size at most $6q^2 + 2q$, with high probability.

One can now easily conclude the termination argument; e.g., the number of (2, 3)- or (3, 4)-2chains that trigger path completions is each at most $2q \cdot (6q^2 + 2q)$ (the product of the maximum size of $P_3$ with the maximum size of $P_2$/$P_4$); or, e.g., the number of (1, 2)-2chains triggered by a pending query $(3,+,\cdot )$ is at most $2q \cdot (6q^2 + 2q)$ (the product of the maximum size of $P_3$ with the maximum size of $P_2$), and so forth.

5.2 Executions of $\mathsf {G}_2$: Definitions and Basic Properties

We start by introducing some notation and establishing properties of executions of $\mathsf {G}_2$. Then, we define a set of bad events that may occur in $\mathsf {G}_2$. An execution of $\mathsf {G}_2$ is good if none of these bad events occur. We will prove that in good executions of $\mathsf {G}_2$, the simulator does not abort and runs in polynomial time.

Queries and 2chains. The central notion for reasoning about the simulator is the notion of 2chain, that we develop below.

Definition 2

A permutation query is a triple $(i,\delta ,z)$ where $1 \le i \le 5$, $\delta \in \{+, -\}$ and $z \in \{0,1\}^n$. We call i the position of the query, $\delta$ the direction of the query, and the pair $(i,\delta )$ the type of the query.

Definition 3

A cipher query is a triple $(\delta ,k,z)$ where $\delta \in \{+, -\}$ and $k, z \in \{0, 1\}^n$. We call $\delta$ the direction and k the key of the cipher query.

Definition 4

A permutation query $(i,\delta ,z)$ is table-defined if $P_i^\delta (z) \ne \bot$, and table-undefined otherwise. Similarly, a cipher query $(\delta , k, z)$ is table-defined if $T^\delta (k,z) \ne \bot$, and table-undefined otherwise.

For permutation queries, we may omit i and $\delta$ when clear from the context and simply say that $x_i$, resp. $y_i$, is table-(un)defined to mean that $(i,+,x_i)$, resp. $(i,-,y_i)$, is table-(un)defined.

Note that if $(i,+,x_i)$ is table-defined and $P_i(x_i) = y_i$, then necessarily $(i,-,y_i)$ is also table-defined and $P_i^{-1}(y_i)=x_i$. Indeed, tables $P_i$ and $P_i^{-1}$ are only modified in procedure Assign, where existing entries are never overwritten due to the check at Line 86. Thus the two tables always encode a partial permutation and its inverse, i.e., $P_i(x_i) = y_i$ if and only if $P_i^{-1}(y_i) = x_i$. In fact, we will often say that a triple $(i,x_i,y_i)$ is table-defined as a shorthand to mean that both $(i,+,x_i)$ and $(i,-,y_i)$ are table-defined with $P_i(x_i)=y_i$, $P_i^{-1}(y_i)=x_i$.

Similarly, if a cipher query $(+,k,x)$ is table-defined and $T(k,x)=y$, then necessarily $(-,k,y)$ is table-defined and $T^{-1}(k,y)=x$. Indeed, these tables are only modified by calls to $\mathrm {Enc}/\mathrm {Dec}$, and always according to the IC tape $\mathsf {ic}$, hence these two tables always encode a partial cipher and its inverse, i.e., $T(k,x)=y$ if and only if $T^{-1}(k,y)=x$. Similarly, we will say that a triple (k, x, y) is table-defined as a shorthand to mean that both $(+,k,x)$ and $(-,k,y)$ are table-defined with $T(k,x)=y$, $T^{-1}(k,y)=x$.

Definition 5

(2chain). An inner 2chain is a tuple $(i,i+1,y_i,x_{i+1},k)$ such that $i\in \{1,2,3,4\}$, $y_i,x_{i+1}\in \{0,1\}^n$, and $k=y_i\oplus x_{i+1}$. A (5,1)-2chain is a tuple $(5,1,y_5,x_1,k)$ such that $y_5,x_1,k\in \{0,1\}^n$. An $(i,i+1)$-2chain refers either to an inner or a (5, 1)-2chain, and is generically denoted $(i,i+1,y_i,x_{i+1},k)$. We call $(i,i+1)$ the type of the 2chain.

Remark 2

Note that for a 2chain of type $(i,i+1)$ with $i\in \{1,2,3,4\}$, given $y_i$ and $x_{i+1}$, there is a unique key k such that $(i,i+1,y_i,x_{i+1},k)$ is a 2chain (hence k is “redundant” in the notation), while for a 2chain of type (5, 1), the key might be arbitrary. This convention allows to have a unified notation independently of the type of the 2chain. See also Remark 3 below.

Definition 6

An inner 2chain $(i,i+1,y_i,x_{i+1},k)$ is table-defined if both $(i,-,y_i)$ and $(i+1,+,x_{i+1})$ are table-defined permutation queries, and table-undefined otherwise. A (5,1)-2chain $(5,1,y_5,x_1,k)$ is table-defined if both $(5,-,y_5)$ and $(1,+,x_1)$ are table-defined permutation queries and if $T(k,x_1)=y_5$, and table-undefined otherwise.

Remark 3

Our definitions above ensure that whether a tuple $(i,i+1,y_i,x_{i+1},k)$ is a 2chain or not is independent of the state of tables $P_i/P_i^{-1}$ and $T/T^{-1}$. Only the fact that a 2chain is table-defined or not depends on these tables.

Definition 7

(endpoints). Let $C=(i,i+1,y_i,x_{i+1},k)$ be a table-defined 2chain. The right endpoint of C, denoted $r(C)$ is defined as

The left endpoint of C, denoted $\ell (C)$ is defined as

We say that an endpoint is dummy when it is equal to $\bot$, and non-dummy otherwise. Hence, only the right endpoint of a 2chain of type (4, 5) or the left endpoint of a 2chain of type (1, 2) can be dummy.

We sometimes identify the right and left (non-dummy) endpoints $r(C)$, $\ell (C)$ of an $(i,i+1)$-2chain C with the corresponding permutation queries $(i+2,+,r(C))$ and $(i-1,-,\ell (C))$. In particular, if we say that $r(C)$ or $\ell (C)$ is “table-defined” this implicitly means that the endpoint in question is non-dummy and that the corresponding permutation query is table-defined. More importantly—and more subtly!—when we say that one of the endpoints of C is “table-undefined” we also implicitly mean that it is non-dummy. (Hence, an endpoint is in exactly one of these three possible states: dummy, table-undefined, table-defined.)

Definition 8

A complete path (with key k) is a 5-tuple of table-defined permutation queries $((1,x_1,y_1),\ldots ,(5,x_5,y_5))$ such that

$$\begin{aligned} y_i \oplus x_{i+1} = k \text { for i = 1, 2, 3, 4 and } T(k, x_1) = y_5. \end{aligned}$$

(4)

The five table-defined queries $(i,x_i,y_i)$ and the five table-defined 2chains $(i,i+1,y_i,x_{i+1},k)$, $i\in \{1,\ldots ,5\}$, are said to belong to the (complete) path.

A 2chain C is also said to be complete if it belongs to some complete path. Note that such a 2chain is table-defined; also, its endpoints $r(C)$, $\ell (C)$ are (non-dummy and) table-defined.

Lemma 3

In any execution of $\mathsf {G}_2$, any 2chain belongs to at most one complete path.

Proof

This follows from the fact that, by definition, a 2chain stipulates a value of k, and from the fact that the tables $P_i/P_i^{-1}$ as well as $T(k,\cdot )/T^{-1}(k,\cdot )$ encode partial permutations.   $\square$

Query Cycles. When the distinguisher makes a permutations query $(i,\delta ,z)$ that is already table-defined, the simulator returns the answer immediately. The definition below introduces some vocabulary related to the simulator’s behavior when the distinguisher makes a permutation query that is table-undefined.

Definition 9

(query cycle). A query cycle is the period of execution between when the distinguisher issues a permutation query $(i_0,\delta _0,z_0)$ which is table-undefined and when the answer to this query is returned by the simulator. We call $(i_0,\delta _0,z_0)$ the initiating query of the query cycle.

A query cycle is called an $(i,i+1)$ -query cycle if the initiating query is of type $(i-1,-)$ or $(i+2,+)$ (see Lemma 4 (a) and Table 1).

The portion of the query cycle consisting of calls to $\mathrm {FindNewPaths}$ at Line 36 is called the detection phase of the query cycle; the portion of the query cycle consisting of calls to $\mathrm {ReadTape}$ at Line 37 and to $\mathrm {AdaptPath}$ at Line 38 is called the completion phase of the query cycle.

Definition 10

(cipher query cycle). A cipher query cycle is the period of execution between when the distinguisher issues a table-undefined cipher query $(\delta , k, z)$ and when the answer to this query is returned. We call $(\delta , k, z)$ the initiating query of the cipher query cycle.

Remark 4

Note that a “query cycle” as defined above is a “permutation query cycle” in the informal description in Sect. 4, and cipher query cycles are not a special case of query cycles. Both query cycles and cipher query cycles require the initiating query to be table-undefined, since otherwise the answer already exists in the tables and is directly returned.

Definition 11

(pending queries, triggered 2chains). During a query cycle, we say that a permutation query ($i,\delta ,z)$ is pending (or that z is pending when i and $\delta$ are clear from the context) if it is appended to list $\mathsf {Pending}$ at Line 35, 58, or 76. We say that a 2chain $C=(i,i+1,y_i,x_{i+1},k)$ is triggered if the simulator appends C to the list $\mathsf {Triggered}$ at Line 55 or 73.

We present a few lemmas below that give some basic properties of query cycles and will help understand the simulator’s behavior.

Lemma 4

During an $(i,i+1)$-query cycle whose initiating query was $(i_0,\delta _0,z_0)$, the following properties always hold:

• (a) Only 2chains of type $(i,i+1)$ are triggered.

• (b) Only permutations queries of type $(i-1,-)$, $(i+2,+)$ become pending.

• (c) Any 2chain that is triggered was table-defined at the beginning of the query cycle.

• (d) At the end of the detection phase, any pending query is either the initiating query, or the endpoint of a triggered 2chain.

• (e) If a 2chain C is triggered during the query cycle, and the simulator does not abort, then C is complete at the end of the query cycle.

Proof

The proof of (a) and (b) proceeds by inspection of the pseudocode: note that calls to $\mathrm {FindNewPaths}(i-1,-,\cdot )$ can only add 2chains of type $(i,i+1)$ to $\mathsf {Triggered}$ and permutations queries of type $(i+2,+)$ to $\mathsf {Pending}$, whereas calls to $\mathrm {FindNewPaths}(i+2,+,\cdot )$ can only add 2chains of type $(i,i+1)$ to $\mathsf {Triggered}$ and permutations queries of type $(i-1,-)$ to $\mathsf {Pending}$. Hence, if the initiating query is of type $(i-1,-)$ or $(i+2,+)$, only 2chains of type $(i,i+1)$ will ever be added to $\mathsf {Triggered}$, and only permutation queries of type $(i-1,-)$ or $(i+2,+)$ will ever be added to $\mathsf {Pending}$. The proof of (c) also follows easily from inspection of the pseudocode. The sole subtlety is to note that for a (5, 1)-query cycle (where calls to $\mathrm {FindNewPaths}$ are of the form $(2,+,\cdot )$ and $(4,-,\cdot )$), for a (5, 1)-2chain to be triggered one must obviously have $x_1\in P_1$ and $y_5\in P_5^{-1}$, but also $T(k,x_1)=y_5$ since otherwise the call to $\mathrm {Check}(k,x_1,y_5)$ would return false. The proof of (d) is also immediate, since for a permutation query to be added to $\mathsf {Pending}$, it must be either the initiating query, or computed at Line 56 or Line 74 as the endpoint of a triggered 2chain. Finally, the proof of (e) follows from the fact that, assuming the simulator does not abort, all values computed during the call to $\mathrm {AdaptPath}(C)$ form a complete path to which C belongs.

Lemma 5

In any execution of $\mathsf {G}_2$, the following properties hold:

• (a) During a (1, 2)-query cycle, tables $T/T^{-1}$ are only modified during the detection phase by calls to $\mathrm {Enc}(\cdot ,\cdot )$ resulting from calls to $\mathrm {Prev}(1,\cdot ,\cdot )$ at Line 56.

• (b) During a (2, 3)-query cycle, tables $T/T^{-1}$ are only modified during the completion phase by calls to $\mathrm {Enc}(\cdot ,\cdot )$ resulting from calls to $\mathrm {Prev}(1,\cdot ,\cdot )$ at Line 83.

• (c) During a (3, 4)-query cycle, tables $T/T^{-1}$ are only modified during the completion phase by calls to $\mathrm {Dec}(\cdot ,\cdot )$ resulting from calls to $\mathrm {Next}(5,\cdot ,\cdot )$ at Line 81.

• (d) During a (4, 5)-query cycle, tables $T/T^{-1}$ are only modified during the detection phase by calls to $\mathrm {Dec}(\cdot ,\cdot )$ resulting from calls to $\mathrm {Next}(5,\cdot ,\cdot )$ at Line 74.

• (e) During a (5, 1)-query cycle, tables $T/T^{-1}$ are not modified.

Proof

This follows by inspection of the pseudocode. The only non-trivial point concerns (1, 2)-, resp. (4, 5)-query cycles, since $\mathrm {Prev}(1,\cdot ,\cdot )$, resp. $\mathrm {Next}(5,\cdot ,\cdot )$ are also called during the completion phase, but they are always called with arguments $(x_1,k)$, resp. $(y_5,k)$ that were previously used during the detection phase, so that this cannot modify the tables $T/T^{-1}$.   $\square$

5.3 Bad Events

In order to define certain bad events that may happen during an execution of $\mathsf {G}_2$, we introduce the following definitions.

Definition 12

($\mathcal {H}$, $\mathcal {K}$ and $\mathcal {E}$). Consider a permutation query $(i_0,\delta _0,z_0)$ or a cipher query $(\delta _0,k_0,z_0)$ made by the distinguisher. The following sets are defined with respect to the state of tables when the query occurs. We define the “history” $\mathcal {H}$ as the multiset consisting of the following elements (each n-bit string may appear and be counted multiple times):

• for each table-defined permutation query $(i, x_i, y_i)$, $\mathcal {H}$ contains corresponding elements $x_i$, $y_i$ and $x_i \oplus y_i$.

• for each table-defined cipher query $(k, x_1, y_5)$, $\mathcal {H}$ contains corresponding elements k, $x_1$ and $y_5$.

We define $\mathcal {K}$ as the multiset of all keys of 2chains triggered in the current query cycle, and $\mathcal {E}$ as the multiset of non-dummy endpoints of all table-defined 2chain plus the value $z_0$ (the query issued by the distinguisher).

Remark 5

When referring to sets $\mathcal {H}$, $\mathcal {K}$ and $\mathcal {E}$ with respect to a query cycle, we mean with respect to its initiating permutation query (and the state of tables at the beginning of the query cycle). These sets are time-dependent, but they don’t change during a query cycle (in particular, the set of triggered 2chains do not depend on the queries that become table-defined during the query cycle). Also note that $\mathcal {K}$ only concerns 2chains triggered in the query cycle, while $\mathcal {E}$ concerns all 2chains that are table-defined at the beginning of the query cycle.

Definition 13

($\mathcal {P}$, $\mathcal {P}^*$, $\mathcal {A}$ and $\mathcal {C}$). Given a query cycle, let $\mathcal {P}$ be the multiset of random values read by ReadTape on tapes $(p_1,p_1^{-1},\ldots ,p_5,p_5^{-1})$ in the current query cycle, and $\mathcal {P}^*$ be the multiset of $x_i \oplus p_i(x_i)$ and $y_i \oplus p_i^{-1}(y_i)$ for each random value $p_i(x_i)$ or $p_i^{-1}(y_i)$ read from the tapes in the current query cycle.

Let $\mathcal {A}$ be the multiset of the values of $x_i \oplus y_i$ for each adapted query $(i, x_i, y_i)$ with $i \in \{2, 4\}$. Note that $\mathcal {A}$ is non-empty only for (4, 5)- and (1, 2)-query cycles.

Given a query cycle or a cipher query cycle, we denote $\mathcal {C}$ the multiset of random values read by $\mathrm {Enc}$ and $\mathrm {Dec}$ on tapes $\mathsf {ic}$ or $\mathsf {ic}^{-1}$.⁹

We define the operations $\cap$, $\cup$ and $\oplus$ of two multisets $\mathcal {S}_1, \mathcal {S}_2$ in the natural way: For each element e that appears $s_1$ and $s_2$ times ($s_1, s_2 \ge 0$) in $\mathcal {S}_1$ and $\mathcal {S}_2$ respectively, $\mathcal {S}_1 \cap \mathcal {S}_2$ contains $\min \{s_1, s_2\}$ copies of e and $\mathcal {S}_1 \cup \mathcal {S}_2$ contains $s_1 + s_2$ copies of e. To define $\mathcal {S}_1 \oplus \mathcal {S}_2$, we start from an empty multiset; for each pair of $e_1 \in \mathcal {S}_1$ and $e_2 \in \mathcal {S}_2$ that appear $s_1$ and $s_2$ times respectively ($s_1, s_2 \ge 1$), add $s_1 \cdot s_2$ copies of $e_1 \oplus e_2$ to the multiset.

Definition 14

Let $\mathcal {H}^{\oplus i}$ be the multiset of values equal to the exclusive-or of exactly i distinct elements in $\mathcal {H}$, and let . The multisets $\mathcal {K}^{\oplus i}$, $\mathcal {E}^{\oplus i}$, $\mathcal {P}^{\oplus i}$, $\mathcal {P}^{* \oplus i}$, $\mathcal {A}^{\oplus i}$ and $\mathcal {C}^{\oplus i}$ are defined similarly.¹⁰

We are now ready to define the afore-mentioned “bad events” on executions of $\mathsf {G}_2$.

Definition 15

BadPerm is the event that at least one of the following occurs in a query cycle:

• $\mathcal {P}^{\oplus i} \cap \mathcal {H}^{\oplus j} \ne \emptyset$ for $i \ge 1$ and $i + j \le 4$;

• $\mathcal {P}^{* \oplus i} \cap \mathcal {H}^{\oplus j} \ne \emptyset$ for $i \ge 1$ and $i + j \le 4$;

• $\mathcal {P}\cap \mathcal {E}\ne \emptyset$, $\mathcal {P}\cap (\mathcal {E}\oplus \mathcal {K}) \ne \emptyset$, $\mathcal {P}\cap (\mathcal {K}\oplus \mathcal {H}) \ne \emptyset$, $\mathcal {P}\cap (\mathcal {K}\oplus \mathcal {H}^{\oplus 2}) \ne \emptyset$;

• $\mathcal {P}^{\oplus 2} \cap \mathcal {K}^{\oplus 2} \ne \emptyset$ or $\mathcal {P}^{\oplus 2} \cap (\mathcal {H}\oplus \mathcal {K}) \ne \emptyset$;

• $\mathcal {P}^*\cap (\mathcal {H}\oplus \mathcal {E}) \ne \emptyset$.

Definition 16

BadAdapt is the event that in a (1, 2)- or (4, 5)-query cycle, $\mathcal {A}^{\oplus i} \cap \mathcal {H}^{\oplus j} \ne \emptyset$ for $i \ge 1$ and $i + j \le 4$.

Definition 17

BadIC is the event that in a query cycle or in a cipher query cycle, either $\mathcal {C}\cap (\mathcal {H}\cup \mathcal {E}) \ne \emptyset$ or $\mathcal {C}$ contains two equal entries.

Note that $\mathcal {P}^{\oplus i}$, $\mathcal {P}^{* \oplus i}$, $\mathcal {A}^{\oplus i}$ and $\mathcal {C}^{\oplus i}$ are random sets built from values read from tapes $(p_1,p_1^{-1},\ldots ,p_5,p_5^{-1})$ and $\mathsf {ic}/\mathsf {ic}^{-1}$ during the query cycle, while $\mathcal {H}^{\oplus i}$, $\mathcal {K}^{\oplus i}$ and $\mathcal {E}^{\oplus i}$ are fixed and determined by the states of the tables at the beginning of the query cycle.

Definition 18

(Good Executions). An execution of $\mathsf {G}_2$ is said to be good if none of BadPerm, BadAdapt and BadIC occurs in the execution.

The main result of this section is to prove that the simulator does not abort in good executions of $\mathsf {G}_2$. Due to space constraints, however, the proof of the following lemma is relegated to the full version [19].

Lemma 6

The simulator does not abort in a good execution of $\mathsf {G}_2$.

5.4 Efficiency of the Simulator

We analyze the running time of the simulator in a good execution of $\mathsf {G}_2$. A large part of this analysis consists of upper bounding the size of tables $T,T^{-1},P_i,P_i^{-1}$. Since $|T|=|T^{-1}|$ and $|P_i|=|P_i^{-1}|$ we state the results only for T and $P_i$.

Note that during a query cycle, any triggered 2chain C can be associated with the query that became pending just before C was triggered and, reciprocally, any pending query $(i,\delta ,z)$, except the initiating query, can be associated with the 2chain C that was triggered just before $(i,\delta ,z)$ became pending. We make these observations formal through the following definitions.

Definition 19

During a query cycle, we say that a 2chain C is triggered by query $(i,\delta ,z)$ if it is added to $\mathsf {Triggered}$ during a call to $\mathrm {FindNewPaths}(i,\delta ,z)$. We say C is an $(i,\delta )$-triggered 2chain if it is triggered by a query of type $(i,\delta )$.

By Lemma 4 (b), a triggered $(i,i+1)$-2chain is either $(i-1,-)$- or $(i+2,+)$-triggered. For brevity, we group 4 special types of triggered 2chains under a common name.

Definition 20

A (triggered) wrapping 2chain is either

• a (4, 5)-2chain that was $(1,+)$-triggered,

• a (1, 2)-2chain that was $(5,-)$-triggered,

• a (5, 1)-2chain that was either $(2,+)$- or $(4,-$)-triggered.

Note that wrapping 2chains are exactly those for which the simulator makes a call to procedure $\mathrm {Check}$ to decide whether to trigger the 2chain or not.

Definition 21

Consider a query cycle with initiating query $(i_0,\delta _0,z_0)$ and a permutation query $(i,\delta ,z)\ne (i_0,\delta _0,z_0)$ which becomes pending. We call the (unique) 2chain that was triggered just before $(i,\delta ,z)$ became pending the 2chain associated with $(i,\delta ,z)$.

Note that uniqueness of the 2chain associated with a non-initiating pending query follows easily from the checks at Lines 57 and 75.

The proof of the following lemma can be found in the full version [19]. The proof relies on the fact that, in a good execution, an $(i, i+1)$-2chain that is complete at the beginning of a query cycle cannot be triggered again in that cycle.

Lemma 7

Consider a good execution of $\mathsf {G}_2$, and assume that a complete path exists at the end of the execution. Then at most one of the five 2chains belonging to the complete path has been triggered during the execution.

Lemma 8

For $i\in \{1,\ldots ,5\}$, the number of table-defined permutation queries $(i,x_i,y_i)$ during an execution of $\mathsf {G}_2$ can never exceed the sum of the number of

• distinguisher’s calls to $\mathrm {Query}(i,\cdot ,\cdot )$,

• $(i+1,i+2)$-2chains that were $(i+3,+)$-triggered,

• $(i-2,i-1)$-2chains that were $(i-3,-)$-triggered,

• $(i+2,i+3)$-2chains that were either $(i+1,-)$- or $(i+4,+)$-triggered.

Proof

Entries are added to $P_i/P_i^{-1}$ either by a call to $\mathrm {ReadTape}$ during an $(i+1,i+2)$- or an $(i-2,i-1)$-query cycle or by a call to $\mathrm {AdaptPath}$ during an $(i+2,i+3)$-query cycle (see Table 1).

We first consider entries that were added by a call to $\mathrm {ReadTape}$ during an $(i+1,i+2)$- or an $(i-2,i-1)$-query cycle. The number of such table-defined queries cannot exceed the sum of the total number $N_{i,+}$ of queries of type $(i,+)$ that became pending during an $(i-2,i-1)$-query cycle and the total number $N_{i,-}$ of queries of type $(i,-)$ that became pending during an $(i+1,i+2)$-query cycle. $N_{i,+}$ cannot exceed the sum of the total number of initiating and non-initiating pending queries of type $(i,+)$ over all $(i-2,i-1)$-query cycles. The total number of initiating queries of type $(i,+)$ is at most the number of distinguisher’s calls to $\mathrm {Query}(i,+,\cdot )$, while the total number of non-initiating pending queries of type $(i,+)$ over all $(i-2,i-1)$-query cycles cannot exceed the total number of $(i-3,-)$-triggered 2chains (as a non-initiating pending query of type $(i,+)$ cannot be associated with an $(i,+)$-triggered $(i-2,i-1)$-2chain). Similarly, $N_{i,-}$ cannot exceed the sum of the total number of distinguisher’s call to $\mathrm {Query}(i,-,\cdot )$ and the total number of $(i-3,-)$-triggered $(i+1,i+2)$-2chains. All in all, we see that the total number of triples $(i,x_i,y_i)$ that became table-defined because of a call to $\mathrm {ReadTape}$ cannot exceed the sum of

• the number of distinguisher’s calls to $\mathrm {Query}(i,\cdot ,\cdot )$,

• the number of $(i+1,i+2)$-2chains that were $(i+3,+)$-triggered,

• the number of $(i-2,i-1)$-2chains that were $(i-3,-)$-triggered.

Consider now a triple $(i,x_i,y_i)$ which became table-defined during a call to $\mathrm {AdaptPath}$ in an $(i+2,i+3)$-query cycle. The total number of such triples cannot exceed the total number of $(i+2,i+3)$-2chains that are triggered over all $(i+2,i+3)$-query cycles (irrespective of whether they are $(i+1,-)$- or $(i+4,+)$-triggered). The result follows.   $\square$

The following lemma contains the standard “bootstrapping” argument introduced in [18]. The proof of the lemma can be found in the full version [19].

Lemma 9

In a good execution of $\mathsf {G}_2$, at most q wrapping 2chains are triggered in total.

Lemma 10

In a good execution of $\mathsf {G}_2$, one always has $|P_3| \le 2q$.

Proof

By Lemma 8, the number of table-defined permutation queries $(3,x_3,y_3)$ (and hence the size of $P_3$) cannot exceed the sum of

• the number of distinguisher’s calls to $\mathrm {Query}(3,\cdot ,\cdot )$,

• the number of (4, 5)-2chains that were $(1,+)$-triggered,

• the number of (1, 2)-2chains that were $(5,-)$-triggered,

• the number of (5, 1)-2chains that were either $(2,+)$- or $(4,-)$-triggered.

The number of entries of the first type is at most q by the assumption that the distinguisher makes at most q oracle queries to each permutation. Further note that any 2chain mentioned for the 3 other types are wrapping 2chains. Hence, by Lemma 9, there are at most q such entries in total, so that $|P_3|\le 2q$.   $\square$

Before proceeding further, we state the following properties of good executions which will be used in the proof of Lemma 13. These properties are proven in the full version [19].

Lemma 11

In a good execution of $\mathsf {G}_2$, for $i \in \{2, 4\}$, there do not exist two distinct table-defined queries $(i,x_i,y_i)$ and $(i,x'_i,y'_i)$ such that $x_i \oplus y_i = x'_i \oplus y'_i$.

Lemma 12

In a good execution of $\mathsf {G}_2$, for $i \in \{2, 4\}$ there never exist four distinct table-defined queries $(i,{x_{i}^{(j)}},{y_{i}^{(j)}})$ with $j = 1,2,3,4$ such that $\sum _{j=1}^4 ({x_{i}^{(j)}} \oplus {y_{i}^{(j)}}) = 0$.

Lemma 13

In a good execution of $\mathsf {G}_2$, the sum of the total numbers of $(3,-)$- and $(5,+)$-triggered 2chains, resp. of $(1,-)$- and $(3,+)$-triggered 2chains, is at most $6q^2-2q$.

Proof

Let C be a 2chain which is either $(3,-)$- or $(5,+)$-triggered during the execution. (The case of $(1,-)$- or $(3,+)$-triggered 2chains is similar by symmetry.) By Lemma 4 (e), C belongs to a complete path $((1,x_1,y_1),\ldots ,(5,x_5,y_5))$ at the end of the execution (since the simulator does not abort), and $C=(3,4,y_3,x_4,k)$ if it was $(5,+)$-triggered, whereas $C=(4,5,y_4,x_5,k)$ if it was $(3,-)$-triggered.

Note that when C was triggered, $(5,+,x_5)$ was necessarily table-defined or pending. If $C=(4,5,y_4,x_5,k)$ was $(3,-)$-triggered, $(5,+,x_5)$ must be table-defined. If $C=(3,4,y_3,x_4,k)$ was $(5,+)$-triggered, then it was necessarily during the call to $\mathrm {FindNewPaths}(5,+,x_5)$ which implies that $x_5$ was pending.

We now distinguish two cases depending on how $(5,+,x_5)$ became table-defined or pending. Assume first that this was because of a distinguisher’s call to $\mathrm {Query}(5,\cdot ,\cdot )$. There are at most q such calls, hence there are at most q possibilities for $x_5$. There are at most 2q possibilities for $y_3$ by Lemma 10. Moreover, for each possible pair $(y_3,x_5)$, there is at most one possibility for the table-defined query $(4,x_4,y_4)$ since otherwise this would contradict Lemma 11 (note that one must have $x_4\oplus y_4=y_3\oplus x_5$). Hence there are at most $2q^2$ possibilities in that case.

Assume now that $(5,+,x_5)$ was a non-initiating pending query in the same query cycle in which C was triggered, or became table-defined during a previous query cycle than the one where C was triggered and for which $(5,+,x_5)$ was neither the initiating query nor became table-defined during the $\mathrm {ReadTape}$ call for the initiating query. In all cases there exists a table-defined (3, 4)-2chain $C'=(3,4,y'_3,x'_4,k')$ distinct from $(3,4,y_3,x_4,k)$ such that $x_5=r(C')=y'_4\oplus x'_4\oplus y'_3$. Since we also have $x_5=y_4\oplus x_4\oplus y_3$, we obtain $x_4 \oplus y_4 \oplus x'_4 \oplus y'_4 = y_3 \oplus y'_3$. If $y_3 = y'_3$, by Lemma 11 we have $x_4 = x'_4$ and $C'=(3,4,y_3,x_4,k) = C$, contradicting our assumption. On the other hand, for a fixed (orderless) pair of $y_3 \ne y'_3$, the (orderless) pair of $(4,x_4,y_4)$ and $(4,x'_4,y'_4)$ is unique by Lemmas 11 and 12 (otherwise, one of the lemmas must be violated by the two pairs). There are at most $\left( {\begin{array}{c}2q\\ 2\end{array}}\right) = q(2q-1)$ choices of $y_3$ and $y'_3$; for each pair there is at most one (orderless) pair of $(4,x_4,y_4)$ and $(4,x'_4,y'_4)$, so there are 2 ways to combine the queries to form two 2chains. Moreover, $C'$ must either have been completed during a previous query cycle than the one where C is triggered, or must have been triggered before C in the same query cycle and have made $x_5$ pending (in which case C was triggered by $(5,+,x_5)$). Thus each way to combine $y_3$, $y'_3$, $(4,x_4,y_4)$ and $(4,x'_4,y'_4)$ to form two 2chains corresponds to at most one $(3,+)$- or $(5,-)$-triggered 2chain, so at most $4q^2 - 2q$ such 2chains are triggered. Combining both cases, the number of $(3,-)$- or $(5,+)$-triggered 2chains is at most $6q^2 - 2q$.

Lemma 14

In a good execution of $\mathsf {G}_2$, $|P_2| \le 6q^2$ and $|P_4| \le 6q^2$.

Proof

By Lemma 8, the number of table-defined queries $(2,x_2,y_2)$ (and hence the size of $P_2$) cannot exceed the sum of

• the number of distinguisher’s calls to $\mathrm {Query}(2,\cdot ,\cdot )$,

• the number of (3, 4)-2chains that were $(5,+)$-triggered,

• the number of (5, 1)-2chains that were $(4,-)$-triggered,

• the number of (4, 5)-2chains that were either $(3,-)$- or $(1,+)$-triggered.

There are at most q entries of the first type by the assumption that the distinguisher makes at most q oracle queries. Any 2chain mentioned for the other cases are either wrapping, $(3,-)$-triggered, or $(5,+)$-triggered 2chains. By Lemmas 9 and 13, there are at most $q+6q^2-2q$ entries of the three other types in total. Thus, we have $|P_2| \le q + q + 6q^2 - 2q = 6q^2$. Symmetrically, $|P_4| \le 6q^2$.   $\square$

Lemma 15

In a good execution of $\mathsf {G}_2$, at most $12q^3$ 2chains are triggered in total.

Proof

Since the simulator doesn’t abort in good executions by Lemma 6, any triggered 2chain belongs to a complete path at the end of the execution. By Lemma 7, at most one of the five 2chains belonging to a complete path is triggered in a good execution. Hence, there is a bijective mapping from the set of triggered 2chains to the set of complete paths existing at the end of the execution. Consider all (3, 4)-2chains which are table-defined at the end of the execution. Each such 2chain belongs to at most one complete path by Lemma 3. Hence, the number of complete paths at the end of the execution cannot exceed the number of table-defined (3, 4)-2chains, which by Lemmas 10 and 14 is at most $2q \cdot 6q^2 = 12q^3$.   $\square$

Lemma 16

In a good execution of $\mathsf {G}_2$, we have $|T| \le 12q^3 + q$.

Proof

Recall that the table T is used to maintain the cipher queries that have been issued. In $\mathsf {G}_2$, no new cipher query is issued in Check called in procedure Trigger. So the simulator issues a table-undefined cipher query only if the path containing the cipher query has been triggered. The number of triggered paths is at most $12q^3$, while the distinguisher issues at most q cipher queries. Thus the number of table-defined cipher queries is at most $12q^3 + q$.   $\square$

Lemma 17

In a good execution of $\mathsf {G}_2$, $|P_1| \le 12q^3 + q$ and $|P_5| \le 12q^3 + q$.

Proof

By Lemma 8, the number of table-defined queries $(1,x_1,y_1)$ (and hence the size of $P_1$) cannot exceed the sum of the number of distinguisher’s call to $\mathrm {Query}(1,\cdot ,\cdot )$, which is at most q, and the total number of triggered 2chains, which is at most $12q^3$ by Lemma 15. Therefore, the size of $|P_1|$ is at most $12q^3 + q$. The same reasoning applies to $|P_5|$.   $\square$

The proof of the following lemma can be found in the full version. It follows in a straightforward manner from the previous lemmas and by inspection of the pseudocode.

Lemma 18

In good executions of $\mathsf {G}_2$, the simulator runs in time $O(q^8)$ and uses $O(q^3)$ space.

Due to space limitations, we present the proofs of the remaining theorems in the full version [19].

5.5 Probability of Good Executions

Theorem 19

An execution of $\mathsf {G}_2$ is good with probability at least

$$ 1 - 4.2 \times 10^8 q^{12} / 2^n. $$

5.6 Indistinguishability of $\mathsf {G}_1$ and $\mathsf {G}_4$

Theorem 20

Any distinguisher with q queries cannot distinguish $\mathsf {G}_1$ from $\mathsf {G}_4$ with advantage more than $2 \times 10^{12}q^{12} / 2^n$.

6 Final Thoughts: 4 and 6 Rounds

We conclude the paper with some more remarks on 4- and 6-round simulators, as a means of providing some extra intuition on our work. The 6-round simulator outlined below is also interesting for reasons of its own, as it achieves significantly better security and efficiency than what we achieve in this paper at 5 rounds.

A Failed 4-Round Simulator. Naturally, any simulator for 4-round iterated Even-Mansour with a non-idealized key schedule can only fail (at least, as long as the distinguisher is allowed to be non-sequential) given the attack presented in Sect. 3. Nonetheless, it can be interesting to review where the indifferentiability proof breaks down if we attempt a straightforward “collapsation” of our 5-round simulator to 4 rounds.

Recall that our 5-round simulator completes chains of length 3. E.g., a forward query $P_3(x_3)$ will cause a chain to be completed for each previously established pair of queries $P_1(x_1) = y_1$, $P_2(x_2) = y_2$ such that $y_1 \oplus x_2 = y_2 \oplus x_3$, and in the course of completing such a chain a new query $P_5^{-1}(y_5)$ will be made and the chain will be adapted at $P_4$. As the $P_5^{-1}$-query may trigger several fresh chain completions of its own, the process recurses, “bouncing back” between chains triggered by $P_3(\cdot )$- and $P_5^{-1}(\cdot )$-queries. Finally, as described, the 5-round simulator actually waits for the recursive process of chain detections to stop before adapting all detected chains at $P_4$, with each detected chain ultimately being adapted at “its own” $P_4$-query.

Similarly, one can imagine a 4-round simulator that attempts to complete all paths of length 3 in the same recursive fashion, but that adapts paths slightly differently: because of the missing round, a path is not adapted by “plugging values in at both ends” of a table $P_i$, but rather by sampling two adjacent values $y_i$, $x_{i+1}$ non-independently such that $y_i \oplus x_{i+1} = k$ where k is the key for the path in question. In a nutshell, the problem with this approach is that because endpoints are shared between paths, simultaneous systems of equations can arise that have no solutions. (In turn, the existence of such unsolvable systems can be traced back to configurations in which “cycles of paths” arise. Such a counterexample can be reconstructed, e.g., from the attack of Sect. 3.)

A 6-Round Simulator. At the opposite, our 5-round simulator enjoys a rather straightforward adaption to 6 rounds. The 6-round version holds some interest because it has a (theoretically) simpler analysis as well as improved efficiency and security.

The basic idea for the 6-round simulator is to detect paths of length 3 as well, but due to the extra round some leeway is afforded, and not all paths need be detected.¹¹ Specifically, the 6-round simulator detects paths at positions 2–3–4, 3–4–5, 6–1–2 and 5–6–1. We shall refer to these position groups as detect zones. For example, a forward query $P_5(x_5)$ for which there exist two previous queries $P_3(x_3) = y_3$ and $P_4(x_4) = y_4$ such that $y_3 \oplus x_4 = y_4 \oplus x_5$ would trigger a path by virtue of the 3–4–5 detect zone. We refer to 2–3–4 and 3–4–5 as the middle detect zones and to 6–1–2 and 5–6–1 as the outer detect zones. One can observe that four distinct detect zones exist, each of which has two “trigger points”. (E.g., the 2–3–4 detect zone is triggered by queries $P_4(\cdot )$ and $P_2^{-1}(\cdot )$.) Structurally this makes the 6-round simulator very similar to the 8-round Feistel simulator of [20] (which was indeed an early source of inspiration for this work).

One can then observe that path completions triggered by either of the middle detect zones do not add queries to positions 3 and 4, while each path triggered by an outer detect zone will require a separate distinguisher query to set up. By a standard termination argument due to Seurin [44], this caps the number of paths completed by the simulator to $O(q^2)$ (the product of the size of $P_3$ and $P_4$), an improvement over the $O(q^3)$ bound from our 5-round simulator. Further, a refined analysis of bad events (some of which can be omitted for the 6-round simulator) pushes security all the way to $O(q^6/2^n)$, a substantial improvement over previous indifferentiability bounds. However, further details are deferred to the full version of this paper.