Keywords

Power supply requirements of consumers located on territories remote from central power supply are of great relevance today. This problem is associated with a range of acute environmental problems determined by considerable emissions resulting from traditional power generation facilities operation (thermal, nuclear, diesel power plants). Therefore, the problems of supplying population with alternative sources of energy are becoming increasingly important. Among the ways to solving this problem, the field of hydropower is considered, first and foremost.

The hydropower current state examination and analysis show that today more than two-third of the hydropower potential from the European Union and the Russian Federation territories is implemented with large HPPs. The extent of larger rivers hydropower potential (HP) exploration is not only determined by extensive hydraulic resources availability, but also the local landscape peculiarities. In particular, the former Soviet republics territories, as well as the eastern and southwestern zones in the Russian Federation are characterized by mountainous regions and, accordingly, high heads. Regarding the question of HP further exploration, one should point out that its unexplored part is constituted by smaller water bodies—plain rivers, various kinds of hydraulic facilities, and retaining/regulating waterworks characterized by low heads and flow low speeds in the channel.

At present, hydraulic units designing which intended for operation in conditions of exactly such sources, as well as the necessity of developing decentralized power supply that determined a return to the global trend to development of small hydropower. It is difficult, and quite probable, impossible to use large hydraulic units at a small rivers HP exploration; therefore, neither is it possible to apply well-elaborated methods of design of such hydraulic units hardly suitable for low-head hydraulic machines.

To solve engineering problems for creating efficient hydraulic machines, it is necessary:

  • to identify the heads and flow rates optimum combinations required for efficient operation of low-power energy generation equipment within a micro-hydraulic power plant;

  • to study the working process proceeding at operation of the same;

  • to perform energy characteristics analysis and optimize the geometry of hydraulic machines;

  • to select perfect design configurations for construction of micro-hydraulic power plants.

Today’s requirements to the quality of electric energy [1, p. 5] are satisfied the most conveniently if the hydraulic unit operates at the rotor high rotation frequency, which is a challenging task in low heads conditions. On the other hand, using low-frequency hydraulic turbine types requires development of efficient low-speed electric generators, or application of multiplicative configurations for their drive. Using multipliers, in its turn, results in a considerable increase in the equipment prime cost comparable to expenses on construction of an entire micro-hydraulic power plant; or (if cheaper multipliers are used) in lower reliability of the micro-hydropower plant and, accordingly, in a considerable rise in operating costs. Therefore, in the view of this paper’s authors, application of micro-hydraulic power plants multiplicative arrangements cannot be considered expedient [2, p. 116; 3, p. 10878]. That is why, to solve the problem, we need to develop technological solutions enabling to use a hydraulic machine with a high rotation frequency, or application of low-speed electric generators. In this context, it is proposed to choose the path of developing an efficient hydraulic machine capable to operate with a high rotation frequency of rotor in conditions of low flow heads. Such solution makes it possible to use the simplest, the most affordable, and reliable device—an asynchronous electric machine—as a generator. A review of the types of hydraulic machines and analysis of their operation in conditions of low heads and low flow rates have shown that axial (Kaplan) blade machines make the most suitable type. To reduce the power unit prime cost, to increase its efficiency and to simplify the design as far as possible, a task is considered for creating a hydraulic unit without guide vanes and with the application of a propeller impeller type.

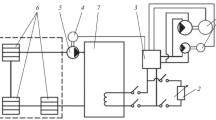
Selection of an energy-efficient design configuration of a micro-hydraulic power plant with Kaplan turbine provides for its being equipped with a device to ensure a sufficiently full conversion of geodetic head into dynamic head, i.e., a considerable increase of the static pressures drop on the hydraulic turbine. A siphon penstock may be used as such device (Fig. 1). Such arrangement enables to locate the hydraulic machine in the flow part of the penstock, with its completely immersed into the working fluid. As distinct from open-design configurations, such layout is protected from intense icing of the structure during the cold season. This enables to operate power units all the year round without losing operability and in much broader natural climatic zones. The problems of creating efficient power units in conditions of low heads force to enhance the power of micro-hydraulic power plants through increasing the plant hydraulic turbine characteristic dimensions of, which, however, cannot be considered an efficient solution. As a way out of the situation in place, it is suggested to use the principle of modularity of the design, which would enable to use a series of units installed in individual penstocks (the so-called modules) within a single hydraulic power plant. This will increase the power of the micro-hydraulic power plant by making it to have a number of hydraulic units, ensuring prolongation of initial capital investments, gradually “increasing” the power to the required level by staged commissioning of the micro-hydraulic power plant modules, and will make such plants more mobile. In order to analyze the efficiency of various design configurations, estimated studies for choosing the place for installation of a hydraulic turbine in the siphon penstock were performed. Analysis of the working process, energy efficiency. and positive suction head of prospective arrangements, presented in Fig. 2, has shown that the arrangements are very close in terms of the above parameters, provided that the energy efficiency factor, and the efficiency of the turbine (to be considered below) are identical. However, layout No. 6 has a clear advantage over all the others, first of all, in terms of operation: the hydraulic turbine impeller immersed into the working fluid makes much more convenient process of starting the micro-hydraulic power plant by brief running the hydraulic unit in the pumping mode for filling the flow part of the siphon penstock. This solution totally eliminates the need to use a complex vacuuming system. Moreover, a propeller hydraulic turbine arranged in the siphon penstock flow part enables to proceed from the pumping mode to the turbine mode (the electric energy generation mode) without the direction reversing of the shaft rotation. This simplifies the micro-hydraulic power plant operating and makes it less structurally complex. The advantages of layout No. 6 lead to considerable reduction of costs and the scope of construction work for creating the same and make it the most promising option for practical application. Therefore, further on, the attention will be mostly focused on its theoretical and experimental studies.

Fig. 1
figure 1

Design of micro-hydraulic power plant with a siphon penstock

Full size image
Fig. 2
figure 2

Arrangement possible options of hydropower unit in the flow part

Full size image

The energy efficiency of a hydraulic turbine in a penstock is assessed involving the use of equations for determination of its power, as well as the intensity of the working fluid flow in the penstock [4, p. 16] according to the designed arrangement as shown in Fig. 3.

Fig. 3
figure 3

Designed layout of the “hydraulic turbine—penstock” complex of micro-hydraulic power plant with a siphon penstock

Full size image

The intensity of the flow, i.e., the working fluid energy passing through the siphon penstock flow part without hydraulic machine can be presented as follows:

$$ N_{s.p.} = \rho gQ_{s.p.} H_{microHPP} , $$
(1)

where

\( H_{microHPP} = z_{US} - z_{DS} \) :

is static head, or gross head [5, p. 15] of the flow in Section 1-1,

\( z_{US} \,{\text{and}}\,z_{DS} \) :

are elevations of the upstream and downstream levels, respectively,

\( Q_{s.p} = F_{s.p.} v_{s.p.} \) :

is flow rate in the penstock without hydraulic machine,

\( F_{s.p.} \) :

is cross-sectional area of the siphon penstock flow part,

\( v_{s.p.} \) :

is flow rate in the penstock without hydraulic machine.

Below is the equation for power implemented on the hydraulic turbine:

$$ N_{ht} = \rho gQ_{ht} H_{theor}^{ht} , $$
(2)

where

\( H_{theor}^{ht} = H_{disp}^{ht} \eta_{hyd} \) :

is theoretical head usefully utilized by the hydraulic turbine (Section 3-3),

\( \eta_{hyd} \) :

is hydraulic efficiency of hydraulic turbine,

\( H_{disp}^{ht} = H_{microHPP} - h_{s.p.} \) :

is disposable head on the hydraulic turbine (Section 2-2),

\( Q_{ht} = Q_{s.p.} \) :

is flow rate through the hydraulic turbine.

To express the factor in relative units, it is necessary to find the ratio between Eqs. (2) and (1):

$$ \frac{{N_{ht} }}{{N_{s.p.} }} = \frac{{\rho gQ_{ht} H_{theor}^{ht} }}{{\rho gQ_{s.p.} H_{microHPP} }}; $$
(3)

With the equation reduced, we have the parameter \( K_{N} \):

$$ K_{N} = \left( {\frac{{v_{f.ht} }}{{v_{s.p.} }}} \right)\left( {\frac{{H_{theor}^{ht} }}{{H_{microHPP} }}} \right); $$
(4)

where \( v_{f.ht} \) is the rate of the flow passing through the hydraulic machine.

The hydraulic turbine located in the penstock creates a considerable hydraulic friction in the same, which results in additional flow energy losses. Therefore, it is necessary to determine losses. This can be done by one of two ways, expressing the losses through:

  1. 1.

    hydraulic loss factor \( \zeta_{ht} \) or

  2. 2.

    additional head losses \( h_{ht}^{II} \) through hydraulic efficiency of the hydraulic turbine,

where it is convenient to use mathematical expressions of these methods as related to the working fluid weight; in this case, these expressions will be as follows (respectively):

$$ h_{ht}^{I} = \zeta_{ht} \frac{{v_{f.ht}^{2} }}{2}; $$
(5)
$$ h_{ht}^{II} = gH_{theor}^{ht} \left( {1 - \eta_{hyd} } \right). $$
(6)

As applied to the “hydraulic turbine—penstock” arrangement under examination, the flow energy losses in the hydraulic turbine must be considered at calculation of the flow velocity in the siphon penstock accommodating a hydraulic turbine. With losses in the hydraulic turbine expressed as head losses (according to p. 2), the equation for the flow velocity will be as follows:

$$ v_{f.ht} = \varphi \sqrt {2g\left( {H_{ht} - H_{theor}^{ht} \left( {1 - \eta_{hyd} } \right)} \right)} ; $$
(7)

With consideration of \( H_{ht} = H_{microHPP} - H_{theor}^{ht} \) and with a head efficiency factor introduced as the ratio of theoretical head to working head

$$ K_{H} = \frac{{H_{theor}^{ht} }}{{H_{microHPP} }}, $$
(8)

the transformed equation will be expressed as Eq. (9):

$$ v_{f.ht} = \varphi \sqrt {2gH_{microHPP} \left( {1 - K_{H} \left( {2 - \eta_{hyd} } \right)} \right)} ; $$
(9)

Now, the ratio of equations for the velocity of flow through the hydraulic turbine (9) to the rate of flow in the water pipeline without the hydraulic machine would give a parameter of the ratio between the flow rates (10):

$$ \begin{aligned} \frac{{v_{f.ht} }}{{v_{s.p.} }} & = \frac{{\varphi \sqrt {2gH_{microHPP} \left( {1 - K_{H} \left( {2 - \eta_{hyd} } \right)} \right)} }}{{\varphi \sqrt {2gH_{microHPP} } }}; \\ \frac{{v_{f.ht} }}{{v_{s.p.} }} & = \sqrt {1 - K_{H} \left( {2 - \eta_{hyd} } \right)} . \\ \end{aligned} $$
(10)

Here Eq. (4) expressed with consideration of (10) gives energy efficiency factor \( K_{N} \) and is presented as follows (11):

$$ K_{N} = K_{H} \sqrt {1 - K_{H} \left( {2 - \eta_{hyd} } \right)} . $$
(11)

Similar considerations with disposable head (instead of theoretic head) enable to determine the value of the maximum energy efficiency factor unambiguously. Then the expression for \( K_{N} \) will be presented as

$$ K_{N} = K_{H} \sqrt {1 - K_{H} } , $$
(12)

here, unlike the Eq. (8) \( K_{N} \) is the ratio of the total head \( H_{t} \) to the static head \( H_{microHPP} \).

The parameter obtained, expressed in relative units, shows the share of usefully utilized energy of the flow by a hydraulic turbine located in a penstock. With this criterion, it is possible to undertake a quantitative comparison of energy efficiency of different micro-hydraulic power plant arrangements comprising a “hydraulic turbine—penstock” complex. Besides, to ensure operation of the micro-hydropower plant in favorable conditions, in terms of energy efficiency (i.e., with the optimum combinations of flow rate, head, and rotation frequency), it is necessary to address the problem of searching for the optimum value of head utilized by the hydraulic turbine usefully. To find its solution, it is important to analyze the behavior of the energy efficiency factor, which can be conveniently presented graphically. Power function \( K_{N} \) in (11) depends on two variables—head efficiency factor \( K_{H} \) and hydraulic efficiency of hydraulic machine \( \eta_{hyd} \).

Therefore, it would make sense to analyze the behavior of \( K_{N} \) for a series of values \( K_{H} \) in the range 0 ÷ 1 for a specific value of \( \eta_{hyd} \). Below are presented the results of calculation of function \( K_{N} = f\left( {K_{H} ,\eta_{hyd} } \right) \) with variation of the parameter \( K_{H} \) within the aforesaid range with an increment 0.1 for a series of hydraulic machines with different hydraulic efficiency in the range 0.5 ÷ 1 with the same increment. The graphic result of computations is presented in Fig. 4. With the graphic relationship plotted, it can be seen that energy efficiency factor \( K_{N} \) has a maximum—the optimum value of head efficiency factor \( K_{Hopt} \), which suggests that there exists an optimum value of the ratio \( \frac{{H_{theor}^{ht} }}{{H_{microHPP} }} \) (according to Eq. (8)), as regards energy efficiency for a particular hydraulic turbine. Parameter \( K_{N} \), according to (12), is the hydraulic efficiency function only \( K_{H} = f\left( {\eta_{hyd} } \right) \) and, as can be seen from the graphic relationship (Fig. 4), it demonstrates the maximum energy efficiency.

Fig. 4
figure 4

Graphical presentation of function \( K_{N} = f\left( {K_{H} ,\upeta_{\varGamma } } \right) \) for a series of \( \upeta_{hyd} \)

Full size image

Examination of function (11) for extremum enables to determine uniquely the optimum ratio of heads for a perfect hydraulic machine with hydraulic efficiency \( \eta_{hyd} = 1 \) located in a siphon penstock. It is worth noting that for such hydraulic turbine the value \( K_{N}^{max} { = 2/3} \cdot \sqrt {\left( { 1- 2 / 3} \right)} \approx 0.3849 \) is limiting and is similar to the Betz–Joukowski limit used in wind energy engineering [6, p. 15]. This conclusion demonstrates that micro-hydraulic power plant with the “hydraulic turbine—penstock” complex achieves energy efficiency maximum and it occurs if the turbine is designed for the total head is equal to two-third of the disposable head \( (H_{opt} = 2 / 3H_{microHPP} ) \).

Experimental studies of the microHPP design configuration with a siphon penstock were performed at NRU “MPEI” involving use a micro-hydropower plant mockup model mounted on an experimental bench (Fig. 5). Power engineering tests enabled to obtain a relation between the maximum power \( N_{ht}^{max} \) of hydraulic turbine and the shaft rotation frequency n (Fig. 6).

Fig. 5
figure 5

Micro-hydraulic power plant mockup model on NRU “MPEI” experimental bench

Full size image
Fig. 6
figure 6

Experimental relations N max  = f (n) and H HT  = f (n) at N max

Full size image

As can be seen from the curve, the hydraulic unit power would reach its maximum at rotation frequency n = 1000 rpm, which is the designed value.

As experimental researches were carried out at different disposable pressure drops on the hydraulic turbine, the results must be reduced to the head design value, i.e., to determine the reduced power \( N_{11} \) [7, p. 472]:

$$ N_{11} = N_{max} \cdot \frac{{H_{opt} }}{H} . $$
(13)

For realistic compliance assessment of obtained hydraulic unit experimental characteristics with designed characteristics, according to Eq. (13), the relation \( N_{11} \)  =  f (n) (Fig. 7) was made for the maximum values of measured power. As can be seen from the curve, \( N_{11}^{max} \) is obtained at n = 1000 rpm and is equal to 1500 W, which is precisely equal to designed characteristics of the hydraulic unit.

Fig. 7
figure 7

Experimental relation N 11  = f (n)

Full size image

Conclusion

The studies presented in the paper enabled to establish analytic relations of the energy useful utilization criterion, which does not only make possible to assess energy efficiency of the micro-hydraulic power plant hydraulic part, but also to take into account the correlation between its head and the working fluid flow rate, which determines the hydraulic turbine power ensuring its designed parameters optimization at early stages of design. Elaboration, analysis, and relevant estimates enabled to identify a structural configuration of micro-hydraulic power plant ensuring considerable costs reduction in construction of new and restoration of out-of-operation small hydraulic power plants, mostly, with a siphon penstock used.

The outlined new approaches to design small hydropower facilities make possible to engage the potential of small water bodies, which is currently virtually unused (less than 1%), while in some regions small hydropower could make the basis of the power supply system. The results of the research present efficient tools for micro-hydropower plants construction, which are characterized by small inundation of lands, which means exerting a lower load on the ecosystem. Moreover, such power plants require lower capital and operation expenses, contribute to creating conditions encouraging construction and restoration of small hydropower facilities in the Russian Federation and Europe, including introduction of obligations on top-priority connection of mini-hydraulic power plants to decentralized power supply grids, and simplification of obtaining permissions for small hydropower facilities construction [8, p. 4].

As a result of the studies indicate, a modular low-head micro-hydraulic power plant is a power supply efficient source of consumers located in decentralized areas and based on renewable sources of energy.