Lectures on Bridgeland Stability

Abstract

In these lecture notes we give an introduction to Bridgeland stability conditions on smooth complex projective varieties with a particular focus on the case of surfaces. This includes basic definitions of stability conditions on derived categories, basics on moduli spaces of stable objects and variation of stability. These notes originated from lecture series by the first author at the summer school Recent advances in algebraic and arithmetic geometry, Siena, Italy, August 24–28, 2015 and at the school Moduli of Curves, CIMAT, Guanajuato, Mexico, February 22–March 4, 2016.

Appendix: Background on Derived Categories

This section contains definition and important properties of the bounded derived category $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ for an abelian category $\mathcal{A}$. Most of the time the category $\mathcal{A}$ will be the category $\mathop{\mathrm{Coh}}\nolimits (X)$ of coherent sheaves on a smooth projective variety X. To simplify notation $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (X)$ will be written for $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathop{\mathrm{Coh}}\nolimits (X))$. Derived categories were introduced by Verdier in his thesis under the supervision of Grothendieck. The interested reader can find a detailed account of the theory in [49], the first two chapters of [61] or the original source [114].

Definition 1

• (1) A complex

  $$\displaystyle{\ldots \rightarrow A^{i-1} \rightarrow A^{i} \rightarrow A^{i+1} \rightarrow \ldots }$$

  is called bounded if A ⁱ = 0 for both i ≫ 0 and i ≪ 0.

• (2) The objects of the category $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ are bounded complexes over $\mathcal{A}$ and its morphisms are homomorphisms of complexes.

• (3) A morphism f: A → B in $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ is called a quasi isomorphism if the induced morphism of cohomology groups H ⁱ(A) → H ⁱ(B) is an isomorphism for all integers i.

The bounded derived category of $\mathcal{A}$ is the localization of $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ by quasi isomorphisms. The exact meaning of this is the next theorem.

Theorem 2 ([61, Theorem 2.10])

There is a category $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ together with a functor $Q:\mathop{ \mathrm{Kom}}\nolimits ^{b}(\mathcal{A}) \rightarrow \mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ satisfying two properties.

• (1) The morphism Q( f) is an isomorphism for any quasi-isomorphism f in the category $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ .

• (2) Any functor $F:\mathop{ \mathrm{Kom}}\nolimits ^{b}(\mathcal{A}) \rightarrow \mathcal{D}$ satisfying property (i) factors uniquely through Q, i.e., there is a unique (up to natural isomorphism) functor $G:\mathop{ \mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A}) \rightarrow \mathcal{D}$ such that F is naturally isomorphic to G ∘ Q.

In particular, Q identifies objects in $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ and $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$. By the definition of quasi isomorphisms we still have well defined cohomology groups H ⁱ(A) for any $A \in \mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$. The category $\mathcal{A}$ is equivalent to the full subcategory of $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ consisting of those objects $A \in \mathcal{A}$ that satisfy H ⁱ(A) = 0 for all i ≠ 0. In the next section we will learn that this is the simplest example of what is known as the heart of a bounded t-structure.

Notice, there is the automorphism $[1]:\mathop{ \mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A}) \rightarrow \mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$, where E[1] is defined by E[1]ⁱ = E ⁱ⁺¹. It simply changes the grading of a complex. Moreover, we define the shift functor [n] = [1]ⁿ for any integer n. The following lemma will be used to actually compute homomorphisms in the derived category.

Lemma 3 ([61, Proposition 2.56])

Let $\mathcal{A}$ be either an abelian category with enough injectives or $\mathop{\mathrm{Coh}}\nolimits (X)$ for a smooth projective variety X. For any $A,B \in \mathcal{A}$ and $i \in \mathbb{Z}$ we have the equality

$$\displaystyle{\mathop{\mathrm{Hom}}\nolimits _{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})}(A,B[i]) =\mathop{ \mathrm{Ext}}\nolimits ^{i}(A,B).}$$

In contrast to $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ the bounded derived category $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ is not abelian. This lead Verdier and Grothendieck to the notion of a triangulated category which will be explained in the next theorem.

Definition 4

For any morphism f: A → B in $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ the cone C( f) is defined by C( f)ⁱ = A ⁱ⁺¹ ⊕ B ⁱ. The differential is given by the matrix

$$\displaystyle{\left (\begin{array}{*{10}c} -d_{A}& 0 \\ f &d_{B} \end{array} \right ).}$$

The inclusion B ⁱ ↪ A ⁱ⁺¹ ⊕ B ⁱ leads to a morphism B → C( f) and the projection B ⁱ ⊕ A ⁱ⁺¹ ↠ A ⁱ⁺¹ leads to a morphism C( f) → A[1].

Definition 5

A sequence of maps F → E → G → F[1] in $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ is called a distinguished triangle if there is a morphism f: A → B in $\mathop{\mathrm{Kom}}\nolimits ^{b}(\mathcal{A})$ and a commutative diagram with vertical isomorphisms in $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ as follows

These distinguished triangles should be viewed as the analogue of exact sequences in an abelian category. If 0 → A → B → C → 0 is an exact sequence in $\mathcal{A}$, then A → B → C → A[1] is a distinguished triangle where the map C → A[1] is determined by the element in $\mathop{\mathrm{Hom}}\nolimits (C,A[1]) =\mathop{ \mathrm{Ext}}\nolimits ^{1}(C,A)$ that determines the extension B. The following properties of the derived category are essentially the defining properties of a triangulated category.

Theorem 6 ([49, Chap. IV])

• (1) Any morphism A → B in $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ can be completed to a distinguished triangle A → B → C → A[1].

• (2) A triangle A → B → C → A[1] is distinguished if and only if the induced triangle B → C → A[1] → B[1] is distinguished.

• (3) Assume we have two distinguished triangles with morphisms f and g making the diagram below commutative.

  

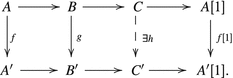
  Then we can find h: C → C′ making the whole diagram commutative.

• (4) Assume we have two morphisms A → B and B → C. Then together with (1) and (3) we can get a commutative diagram as follows where all rows and columns are distinguished triangles.

  

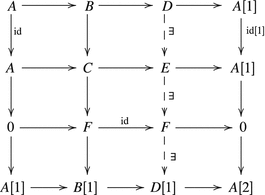
The key in property (4) is that the triangle D → E → F → D[1] is actually distinguished. Be aware that contrary to most definitions in category theory the morphism in (3) is not necessarily unique.

Exercise 7

Let A → B → C → A[1] be a distinguished triangle and $E \in \mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$ be an arbitrary object. Then there are long exact sequences

$$\displaystyle{\ldots \rightarrow \mathop{\mathrm{Hom}}\nolimits (E,C[-1]) \rightarrow \mathop{\mathrm{Hom}}\nolimits (E,A) \rightarrow \mathop{\mathrm{Hom}}\nolimits (E,B) \rightarrow \mathop{\mathrm{Hom}}\nolimits (E,C) \rightarrow \mathop{\mathrm{Hom}}\nolimits (E,A[1]) \rightarrow \ldots }$$

and

$$\displaystyle{\ldots \rightarrow \mathop{\mathrm{Hom}}\nolimits (A[-1],E) \rightarrow \mathop{\mathrm{Hom}}\nolimits (C,E) \rightarrow \mathop{\mathrm{Hom}}\nolimits (B,E) \rightarrow \mathop{\mathrm{Hom}}\nolimits (A,E) \rightarrow \mathop{\mathrm{Hom}}\nolimits (C[-1],E) \rightarrow \ldots }$$

Show the existence of one of the two long exact sequences (their proofs are almost the same).

Exercise 8

Let f: A → B be a morphism in $\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (\mathcal{A})$. Show that f is an isomorphism if and only if C = 0.

Exercise 9

Prove the corresponding statement to the Five Lemma for derived categories: Assume there is a commutative diagram between distinguished triangles

If two of the morphisms f, g, h are isomorphisms, so is the third one.

We will need the following technical statement in the main text.

Proposition 10 ([33, Proposition 5.4])

Let X be a smooth projective variety and $E \in \mathop{\mathrm{D}^{\mathrm{b}}}\nolimits (X)$ . If $\mathop{\mathrm{Ext}}\nolimits ^{i}(E, \mathbb{C}(x)) = 0$ for all x ∈ X and i < 0 or $i> s \in \mathbb{Z}$ . Then E is isomorphic to a complex F ^• of locally free sheaves such that F ⁱ = 0 for i > 0 and i < −s.

All triangles coming up in this article are distinguished. Therefore, we will simply drop the word distinguished from the notation.