Pipette Hunter: Patch-Clamp Pipette Detection

Abstract

Segmentation of objects with known geometries in an image is a wide research area. In this paper we show an energy minimization model to detect the tip of glass pipettes in microscopy images. The described model fits two rectangles with a common reference point to dark image regions, which are the sides of a pipette. The model is minimized using gradient descent. The low number of parameters result in a fast evolution and noise insensitivity. The algorithm is tested on label-free and fluorescent microscopy images. The error of the tip detection is only a few micrometers. Automatic pipette tip detection is a step forward to automate the patch-clamping process. The described method can be extended to 3 dimensions or other applications.

1 Introduction

Segmentation of objects with well defined geometries is a vital problem in image analysis. Several methods were proposed to detect lines, ellipses or rectangles to identify roads [6], trees [11], or houses [7], respectively using marked point processes. Another way is to compromise strict geometries and use variational methods. For example higher order active contours (HOAC) that can describe various objects with defined shape allowing slight variations of the boundaries. HOACs were successfully used to model circular objects [9] or complex road structures [12]. Recently a family of hybrid variational models was proposed [13, 14] that is capable of capturing circular and elliptical objects by minimizing only a few parameters. Here we present a variational method that extends the latter model to detect elongated straight object pairs that have a common reference point. We use this model to segment pipette tips under a microscope and automatically navigate these tips with micrometer precision for patch-clamping and measure properties of neuron cells.

Patch-clamping is a technique to study ion channels in cells. The technique was invented by Erwin Neher and Bert Sakmann in the early 1980s who received the Nobel Prize in Physiology or Medicine in 1991 for their work. Although the technique can be applied to a wide variety of cells, it is especially useful for measuring the electrophysiological properties of nerve cells (neurons).

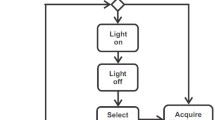
The schematic process of patch-clamping a single cell is the following. A glass pipette is pulled onto an electrode. The tip of the glass pipette is open, thus the measured signal originates only from the pipette tip, because the glass does not transfer electricity. The pipette is then pushed next to a cell. When a tight connection, called ‘gigaseal’ is formed between the cell and the pipette, the cell membrane is broken by vacuum or relatively high voltage pulses. This way the whole-cell patch-clamping configuration is established as illustrated in Fig. 1, the electric signal is passed to an amplifier and then it is ready to be recorded.

Fig. 1.

Schematic whole-cell patch-clamping.

The patch-clamping process has to be repeated manually for every target cell. Experienced biologists can usually do only 10–30 successful patch-clamping a day. The process is repetitive and monotonous, thus error prone as the researchers get fatigued. Recently, efforts have been made to automate the technique. In [3] authors used their automatic patch-clamp setup for in vivo applications. In [10] the authors extended the technique to a multi-electrode system using up to 12 pipettes. A MATLAB implementation of an automatic patch-clamp software is publicly available [2]. A detailed description of building an automatic patch-clamp setup can be found in [4]. In [1] automatic patch-clamping has been successfully used for cardiomyocytes. An issue of automatic patch-clamping is that glass pipettes has to be changed after every patch-clamping, limiting the throughput. In [5] the authors show a way to clean the pipettes which allows them to be used about 10 times. Patch-clamping is often used in tissue slices when there is an imaging modality to see the target cells and the pipette, unlike to in vivo applications. However, changing the pipettes introduces another problem. The pipettes are not perfectly identical and the tip can be slightly translated after the change. In [8] a method is proposed for automatic pipette tip detection using fluorescent channels. However, fluorescent materials can damage cell functions and are not always applicable. Recently, a method for pipette detection in label-free microscopy was proposed in combination with fluorescent cell detection in tissues [15]. The method is used in low magnification (4x) which provides sharp image of the pipette due to the relatively thick focus plane, even if it is tilted. The detection is based on finding intersecting lines using Hough transform, which calculates the lateral position of the tip. The z position is refined using a focus detection algorithm.

In this paper we propose a novel pipette tip detection algorithm using energy minimization. The method works for differential interference contrast (DIC) and oblique microscopy image stacks that contain optically sliced images of a pipette. These microscopy techniques provide dark image regions at the edge of the glass pipette. The method tries to fit two line segments with a common end point on the different projections of the image stack. The idea of fitting a primitive shape to the image is inspired by the Snakuscule [14] algorithm that segments circular objects. Besides the exact location of the tip’s endpoint in 3D, our detection algorithm determines the orientation and tilt angle as well. The algorithm can be extended to fluorescent pipette tip detection, after an edge detection preprocessing step.

2 Methods

Our tip detection method relies on the image formation of DIC (and similarly of oblique) microscopy. DIC is able to show very small optical path length differences of the objects. Diffraction, refraction, reflection and too high optical path length differences can cause effects that are not shown correctly by DIC. The light rays hit the sides of the pipette in a very flat angle, which results in strong effects of the mentioned principles. Due to these side-effects, the regions of pipette edges in the image will be dark, which is information about the position of the pipette. Our method relies on this observation. The pipette is usually not completely in focus in a single image, which is illustrated in Fig. 2a–b. We have developed a 2D model that works on a minimum intensity projection (MIP) of an image stack. The MIP image contains dark stripes in the position of the pipette edges as shown in Fig. 2c. We apply the proposed algorithm for all three possible projection directions to determine the exact position of the pipette tip.

Fig. 2.

Example images of a pipette. (a) The pipette tip is nearly in focus. (b) The z level is moved 20 micrometers up compared to (a). (c) Minimum intensity projection along the third dimension of the stack image.

2.1 The Pipette Hunter

The pipette capturing configuration is illustrated in Fig. 3. Let $\mathbf {i}$ and $\mathbf {j}$ define our standard basis at the image origin. The coordinates in the standard basis are denoted by $x^{1}$, $x^{2}$ and $I(x^{1},x^{2})$ is the image data. The main idea is to cover dark image regions (the edges of the pipette) with two wide rectangles given some constraints. The rectangles are aligned with two line segments that have a common end point, also called as pivot point. The pivot point is the reference point of the two rectangles. The line segments are called legs. The pivot point is given by its position vector $\mathbf {r}=x^{1}\mathbf {i}+x^{2}\mathbf {j}$. The rotation of the legs around the pivot point $\varphi ^{1}$, $\varphi ^{2}$ are measured from the $\mathbf {i}$ axis in the positive direction. The unit direction vectors of the legs are noted as $\mathbf {e}_{1},\mathbf {e}_{2}$ and their unit normals as $\mathbf {n}_{1},\mathbf {n}_{2}$ respectively. $\xi _{i1}$ and $\xi _{i2}$ are distances from the pivot point in the direction of $\mathbf {e}_{i}$ that define the placement along the leg and the length of a rectangle ($i\in \{1,2\}$, $\xi _{i2}>\xi _{i1}\ge 0$). $\eta _{i1}$ and $\eta _{i2}$ are distances in the normal directions that define the perpendicular placement and the thickness of a rectangle ($i\in \{1,2\}$, $\eta _{i2}>\eta _{i1}$). Note, that $\eta$ values can be given such that the rectangles are not symmetric to the legs, which will allow fine tuning of the pivot point later in the algorithm. The model has 4 degrees-of-freedom (DOF), 2 for the coordinates of $\mathbf {r}$ and 1-1 for $\varphi ^{1}$ and $\varphi ^{2}$.

Fig. 3.

The pipette hunter.

2.2 The Associated Extreme-Value Problem

The points of the rectangles $\mathbf {p}_{i}$, $i\in \{1,2\}$ can be decomposed either in the directions of the standard basis vectors or in the directions defined by their respective legs such that

$$\begin{aligned} \mathbf {p}_{i}&=\mathbf {r}+\xi _{i}\mathbf {e}_{i}+\eta _{i}\mathbf {n}_{i}\nonumber \\&=\left[ x^{1}+\xi _{i}\left( \cos \varphi ^{i}\right) -\eta _{i}\left( \sin \varphi ^{i}\right) \right] \mathbf {i}+\left[ x^{2}+\xi _{i}\left( \sin \varphi ^{i}\right) +\eta _{i}\left( \cos \varphi ^{i}\right) \right] \mathbf {j}\\&=\left[ x^{1}\left( \cos \varphi ^{i}\right) +x^{2}\left( \sin \varphi ^{i}\right) +\xi _{i}\right] \mathbf {e}_{i}+\left[ -x^{1}\left( \sin \varphi ^{i}\right) +x^{2}\left( \cos \varphi ^{i}\right) +\eta _{i}\right] \mathbf {n}_{i},\nonumber \end{aligned}$$

(1)

where $\xi _{i}$ and $\eta _{i}$ are the local coordinates w.r.t. the pivot point. The area of the two rectangles can be simply given as:

$$\begin{aligned} A=\sum _{i=1}^{2}\left( \xi _{i2}-\xi _{i1}\right) \left( \eta _{i2}-\eta _{i1}\right) . \end{aligned}$$

(2)

We define the energy of the described system as the sum of the energies of the individual legs $E=\sum _{i=1}^{2}E_{i}$:

$$\begin{aligned} E\left( x^{1},x^{2},\varphi ^{1},\varphi ^{2}\right) \doteq \sum _{i=1}^{2}\frac{1}{A}\mathop {\int }\limits _{\eta _{i}=\eta _{i1}}^{\eta _{i2}}\mathop {\int }\limits _{\xi _{i}=\xi _{i1}}^{\xi _{i2}}f(\xi _{i},\eta _{i})I\left( \mathbf {p}_{i}\right) d\xi _{i}d\eta _{i}, \end{aligned}$$

(3)

where f is an appropriately chosen function representing any filter that rotates with the legs. Note that upper indices indicate variables on which the energy depends and are not powers. The easiest way to understand the energy function is to consider f to be identical to 1. In this case the energy is low when the mean image intensity under the rectangles defined by the Pipette Hunter is low. The components of the energy gradient w.r.t. the coordinates of the pivot point are:

$$\begin{aligned} \frac{\partial E}{\partial x^{1}}&=\frac{\partial E}{\partial \mathbf {r}}\cdot \mathbf {i}\nonumber \\ \frac{\partial E}{\partial x^{2}}&=\frac{\partial E}{\partial \mathbf {r}}\cdot \mathbf {j}, \end{aligned}$$

(4)

where $\frac{\partial E}{\partial \mathbf {r}}\cdot \mathbf {b}$ is the scalar (dot) product of the gradient vector $\frac{\partial E}{\partial \mathbf {r}}\equiv E\nabla$ with one of the standard basis vectors $\mathbf {b}\in \left\{ \mathbf {i},\mathbf {j}\right\}$. The gradient vector itself is a sum of two vectors (i.e. the coordinates of the pivot point dependent on the energies of both legs), each of them can be decomposed in the directions of its own leg, such that the integration boundaries become constants:

$$\begin{aligned} \frac{\partial E}{\partial \mathbf {r}}&=\sum _{i=1}^{2}\left[ \left( \frac{\partial E_{i}}{\partial \mathbf {r}}\cdot \mathbf {e}_{i}\right) \mathbf {e}_{i}+\left( \frac{\partial E_{i}}{\partial \mathbf {r}}\cdot \mathbf {n}_{i}\right) \mathbf {n}_{i}\right] . \end{aligned}$$

(5)

The energy gradient w.r.t. the rotations $\varphi ^{1}$ and $\varphi ^{2}$ are:

$$\begin{aligned} \frac{\partial E}{\partial \varphi ^{i}}&=\sum _{j=1}^{2}\frac{1}{A}\mathop {\int }\limits _{\eta _{j}=\eta _{j1}}^{\eta _{j2}}\mathop {\int }\limits _{\xi _{j}=\xi _{j1}}^{\xi _{j2}}f\left( \xi _{j},\eta _{j}\right) I\nabla \left( \mathbf {p}_{j}\right) \cdot \frac{\partial \mathbf {p}_{j}}{\partial \varphi ^{i}}d\xi _{j}d\eta _{j}. \end{aligned}$$

(6)

From Eq. (1), the derivatives of the position vector $\mathbf {p}_{j}$ are:

$$\begin{aligned} \frac{\partial \mathbf {p}_{j}}{\partial \varphi ^{i}}&=\delta _{ij}\left\{ \xi _{j}\left[ -\left( \sin \varphi ^{i}\right) \mathbf {i}+\left( \cos \varphi ^{i}\right) \mathbf {j}\right] +\eta _{j}\left[ -\left( \cos \varphi ^{i}\right) \mathbf {i}-\left( \sin \varphi ^{i}\right) \mathbf {j}\right] \right\} \nonumber \\&=\delta _{ij}\left( \xi _{j}\mathbf {n}_{i}-\eta _{j}\mathbf {e}_{i}\right) . \end{aligned}$$

(7)

where $\delta _{ij}$ is the Kronecker delta function, indicating that (unlike the pivot coordinates) the rotations of the legs contribute to the system energy independently.

Using Eqs. (4–7) and (a) the following identities $\mathbf {i\cdot e}_{i}=\cos \varphi ^{i}$, $\mathbf {i\cdot n}_{i}=-\sin \varphi ^{i}$, $\mathbf {j\cdot e}_{i}=\sin \varphi ^{i}$, $\mathbf {j\cdot n}_{i}=\cos \varphi ^{i}$, (b) the definitions of the directional derivatives $I_{\xi _{_{i}}}=I\nabla \cdot \mathbf {e}_{i}$, $I_{\eta _{_{i}}}=I\nabla \cdot \mathbf {n}_{i}$, the complete system is written as:

$$\begin{aligned} \frac{\partial E}{\partial x^{1}}&=\frac{1}{A}\sum _{i=1}^{2}\mathop {\int }\limits _{\eta _{i1}}^{\eta _{i2}}\mathop {\int }\limits _{\xi _{i1}}^{\xi _{i2}}f\left( \xi _{i},\eta _{i}\right) \left[ \cos \varphi ^{i}I_{\xi _{i}}\left( \mathbf {p}_{i}\right) -\sin \varphi ^{i}I_{\eta _{i}}\left( \mathbf {p}_{i}\right) \right] d\xi _{i}d\eta _{i}\nonumber \\ \frac{\partial E}{\partial x^{2}}&=\frac{1}{A}\sum _{i=1}^{2}\mathop {\int }\limits _{\eta _{i1}}^{\eta _{i2}}\mathop {\int }\limits _{\xi _{i1}}^{\xi _{i2}}f\left( \xi _{i},\eta _{i}\right) \left[ \sin \varphi ^{i}I_{\xi _{i}}\left( \mathbf {p}_{i}\right) +\cos \varphi ^{i}I_{\eta _{i}}\left( \mathbf {p}_{i}\right) \right] d\xi _{i}d\eta _{i}\\ \frac{\partial E}{\partial \varphi ^{i}}&=\frac{1}{A}\mathop {\int }\limits _{\eta _{i1}}^{\eta _{i2}}\mathop {\int }\limits _{\xi _{i1}}^{\xi _{i2}}f\left( \xi _{i},\eta _{i}\right) \left[ \xi _{i}I_{\eta _{i}}\left( \mathbf {p}_{i}\right) -\eta _{i}I_{\xi _{i}}\left( \mathbf {p}_{i}\right) \right] d\xi _{i}d\eta _{i},\quad i=1,2.\nonumber \end{aligned}$$

(8)

2.3 Simplification

Consider the simple case when no filter function is used: $f\left( \xi _{i},\eta _{i}\right) \equiv 1$. Then the calculations will be limited to the boundaries of the rectangles. By using filters, the calculations can be expanded to the internal regions of the rectangles. Our simplified model uses no filter function. Let the primed $\xi '$, $\eta '$ variables note the variables measured from the origin of the standard basis in the directions of the respective local systems $\mathbf {e}_{i}$, $\mathbf {n}_{i}$, i.e. $\left( \xi _{i}',\eta _{i}'\right) =\left( \mathbf {e}_{i}\cdot \mathbf {r}+\xi _{i},\,\mathbf {n}_{i}\cdot \mathbf {r}+\eta _{i}\right)$. Note that the primed variables $\xi '$, $\eta '$ differ from their unprimed counterparts only by a displacement, hence $d\xi =d\xi '$, $d\eta =d\eta '$. The gradient components of the energy w.r.t. the pivot point (i.e. the first two lines of the extreme value Eqs. (8)) become single integrals:

$$\begin{aligned} \frac{\partial E}{\partial x^{1}}&=\frac{1}{A}\sum _{i=1}^{2}\left( \cos \varphi ^{i}\mathop {\int }\limits _{\eta _{i}=\eta _{i1}}^{\eta _{i2}}I\left( \xi _{i2}',\eta _{i}'\right) -I\left( \xi _{i1}',\eta _{i}'\right) d\eta _{i}\right. \nonumber \\&\quad \quad \quad \left. -\sin \varphi ^{i}\mathop {\int }\limits _{\xi _{i}=\xi _{i1}}^{\xi _{i2}}I\left( \xi _{i}',\eta _{i2}'\right) -I\left( \xi _{i}',\eta _{i1}'\right) d\xi _{i}\right) \nonumber \\ \frac{\partial E}{\partial x^{2}}&=\frac{1}{A}\sum _{i=1}^{2}\left( \sin \varphi ^{i}\mathop {\int }\limits _{\eta _{i}=\eta _{i1}}^{\eta _{i2}}I\left( \xi _{i2}',\eta _{i}'\right) -I\left( \xi _{i1}',\eta _{i}'\right) d\eta _{i}\right. \\&\quad \quad \quad \left. +\cos \varphi ^{i}\mathop {\int }\limits _{\xi _{i}=\xi _{i1}}^{\xi _{i2}}I\left( \xi _{i}',\eta _{i2}'\right) -I\left( \xi _{i}',\eta _{i1}'\right) d\xi _{i}\right) .\nonumber \end{aligned}$$

(9)

Note, that the integrands are the differences of the image intensity values on the regions’ opposite boundaries (that is, the opposite edges of the rectangles).

Similarly, the gradient components of the energy w.r.t. the angles $\varphi ^{1}$, $\varphi ^{2}$ (the third line of the extreme value Eqs. (8)) become:

$$\begin{aligned} \frac{\partial E}{\partial \varphi ^{1}}&=\frac{1}{A}\left( \mathop {\int }\limits _{\xi _{1}=\xi _{11}}^{\xi _{12}}\xi _{1}\left[ I\left( \xi _{1}',\eta _{12}'\right) -I\left( \xi _{1}',\eta _{11}'\right) \right] d\xi _{1}\right. \nonumber \\&\quad \quad \;\left. -\mathop {\int }\limits _{\eta _{1}=\eta _{11}}^{\eta _{12}}\eta _{1}\left[ I\left( \xi _{12}',\eta _{1}'\right) -I\left( \xi _{11}',\eta _{1}'\right) \right] d\eta _{1}\right) \nonumber \\ \frac{\partial E}{\partial \varphi ^{2}}&=\frac{1}{A}\left( \mathop {\int }\limits _{\xi _{2}=\xi _{21}}^{\xi _{22}}\xi _{2}\left[ I\left( \xi _{2}',\eta _{22}'\right) -I\left( \xi _{2}',\eta _{21}'\right) \right] d\xi _{2}\right. \\&\quad \quad \;\left. -\mathop {\int }\limits _{\eta _{2}=\eta _{21}}^{\eta _{22}}\eta _{2}\left[ I\left( \xi _{22}',\eta _{2}'\right) -I\left( \xi _{21}',\eta _{2}'\right) \right] d\eta _{2}\right) .\nonumber \end{aligned}$$

(10)

Note that unlike in the case of the pivot equations, the integrands (of the single integrals) are the weighted differences of the image intensity values on the regions’ opposite boundaries (that is, the opposite edges of the rectangles).

2.4 Solving the Equations

One way to minimize the energy $E\left( q^{i}\right)$ of a system that depends on general variables $q^{i}$, $i=1,2,...n$ is to find the stationary solution for the gradient descent evolution equation: $\frac{\partial q^{i}}{\partial \tau }=-\frac{\partial E}{\partial q^{i}}$, where $\tau$ is the ‘artificial’ time, and at the stationary point $\frac{\partial q^{i}}{\partial \tau }=0$ (hence $\frac{\partial E}{\partial q^{i}}=0$).

In our case, the dimensions of the pivot point Eqs. (9) and the rotation angle Eqs. (10) are different. The first two is expressed in length units, while the second two is in radians. Thus we perform a normalization. The complete system, using the local coordinate system, consists of four coupled differential equations:

$$\begin{aligned} \frac{\partial x^{1}}{\partial \tau }&=-\frac{\partial E}{\partial x^{1}}\nonumber \\ \frac{\partial x^{2}}{\partial \tau }&=-\frac{\partial E}{\partial x^{1}}\nonumber \\ \frac{\partial \varphi ^{1}}{\partial \tau }&=-\frac{2}{\left( \xi _{11}+\xi _{12}\right) }\frac{\partial E}{\partial \varphi ^{1}} \\ \frac{\partial \varphi ^{2}}{\partial \tau }&=-\frac{2}{\left( \xi _{21}+\xi _{22}\right) }\frac{\partial E}{\partial \varphi ^{2}}.\nonumber \end{aligned}$$

(11)

The quantities on the right hand side are defined in (9) and (10).

2.5 Properties and Notes

The Pipette Hunter is neutral (does nothing) in a homogeneous environment. Weak ‘external forces’ (constants to Eq. (11)) may be added to avoid freezing in these regions.

In the simplified case, the integrals are calculated only on the edges of the rectangle shaped region, hence only the image intensity distribution at the boundary is taken into account. The intensity function can freely vary inside. This is not always acceptable. To impose some regularity requirements inside the rectangles, an appropriate filter function can be applied, hence the general equations in (8) need to be used. Minimizing the most significant Fourier coefficients of the intensity function (i.e. using a combination of the Fourier basis functions as a filter) allows minor variance inside the rectangles.

3 Results

We have implemented (11) in MATLAB. If some part of the legs are outside the image boundaries, we use the median value of the image for calculations, which is usually very close to the background intensity. For $\xi _{i1}$ we use 0, and for the length of the legs ($\xi _{i2} - \xi _{i1}$) we use half of the longer side of the image. We find this value to work well when the pipette covers about half of the image (it can be the shorter side as well) or even goes over it.

The $\eta$ values should be chosen such that if a rectangle is fit on a pipette edge, its sides that are aligned to $\mathbf {e}_i$ lie on the opposite sides of the dark region. For our tests we have empirically set 15 pixels for both $\eta$ values which satisfied the above requirement, and thus the sides are symmetric to the corresponding leg. Note, that the distance between the sides ($\eta _{i1} + \eta _{i2}$) becomes 30 pixels. If this distance is too short, the algorithm is not able to fit the model on dark regions. Similarly, if the distance is too high, the result can be inaccurate.

Fig. 4.

Images captured during the runtime of the algorithm. Red dashed lines are the starting position of the legs, which is kept in all the images for comparison. White dashed lines are the current state of the legs. (a) During the first phase, both the introduced force and the image intensities pull the legs towards the dark regions. (b) End of the first phase. (c) In the second phase the pivot point is also updated. The legs are moved and rotated to cover darker image regions. (d) The result of the detection.

We start multiple instances of the Pipette Hunter mechanism in swarm to cover the whole image, which is not possible by using only 2 legs. A simple swarm setup is to place a few mechanisms with different rotations on grid points over the image. This number can be minimized to keep the runtime low. As we require the pipette to be around or over the center of the image and set the length of the legs to be half of the longer side of the image, putting mechanisms to the sides and the center of the image will be enough to find the pipette region with at least one instance. Note, that this is a specific case and the search can fail if the requirements are not satisfied. In the general case where no assumption is made on the pipette’s position, the runtime can be much higher as it depends on the number of instances in the swarm. Furthermore, we use a 2-phase run of the algorithm. In the first phase, we only update the angles and apply a force that pulls the two legs towards each other. The phase ends if the angles’ changes are small or the legs get closer to each other than 0.1 rad. This allows the initialization of an instance with high angle difference (even $\pi / 2$ rad or more). In the second phase we turn off the pulling force, update the pivot point as well and keep the restriction that does not let the legs get too close to each other. A few iterations of the algorithm on an example image using one mechanism is shown in Fig. 4.

3.1 Comparisons

To compare the detection of the Pipette Hunter to a reliable solution, we have manually determined the pipette tip positions in 31 stack images. Figure 5 contains images where the pipette orientation and the starting points of the algorithm differs. The average absolute difference between the algorithm’s result and the hand-picked focus points is 3.53 ± 2.47 $\upmu \mathrm{{m}}$, which is 32.97 ± 23.10 pixels and the image size was 1388 by 1040 pixels. This error is acceptable in automatic patch-clamping. A cell’s diameter is 10–20 $\upmu \mathrm{m}$. If the pipette tip is aimed at the cell’s centroid, given the above error it will still reliably hit the cell. Furthermore, our results are better than the value reported in [8] for final tip-target distance in in vitro experiments, which was 12.06 ± 4.30 $\upmu$m.

Fig. 5.

Example configurations and results.

We have developed a simple baseline algorithm which can be compared to our method. The baseline model also searches for dark image regions. The model works if the pipette orientation is 0 rad. First, the algorithm searches for minimum point-pairs in the y direction in every slice, then fits two lines on them. The intersection of the two lines will be considered as the pipette tip. The algorithm has a linear runtime, but poor in quality. The baseline model often over-detects the pipette tip, which is illustrated in Fig. 6 and compared to the proposed model. On 15 appropriate image stacks (where the pipette orientation is 0 rad.) the mean absolute difference to the hand-picked solutions is 17.92 ± 9.49 $\upmu$m (167.52 ± 88.68 pixels).

Fig. 6.

Comparison to the baseline algorithm (left) on the same image stack.

Fig. 7.

Example fluorescent images and the detection result. (a) Images of a fluorescent pipette in different z-levels and the projected fluorescent image. (b) The projected image filtered with the Sobel operator. (c) Result of the pipette detection algorithm.

3.2 Application on Fluorescent Images

Patch-clamping is sometimes performed in two-photon (fluorescent) imaging mode. The proposed pipette detection method can be applied on fluorescent images after applying an edge detection filter (e.g. Sobel detector in our case) and inverting the image. The edges of the pipette will be dark regions. Figure 7 shows the algorithm applied on a fluorescent image after the discussed preprocessing steps. Because the dark regions are narrow, we used smaller $\eta$ values and longer legs.

4 Discussion

In this paper an energy minimization framework has been proposed for patch-clamp pipette detection. The method works on minimum intensity projection of DIC images. The main idea is to fit rectangles on dark image regions that are the sides of the pipette. The algorithm can be applied in automated patch-clamping, where the pipette has to be changed often and slight changes in the pipette’s length and shape can be detected in a robust way. The result includes the pipettes orientation and tilt angle as well. The steps of the algorithm are presented on example images. The results are compared to hand-picked pipette tip positions and to a baseline algorithm. After a preprocessing step, the approach can also be applied to fluorescent images. Further work includes extension to 3D, which will work on stack images and directly return an (x,y,z) point, both on DIC and fluorescent images. We believe our method can be extended to other applications, e.g. road intersection detection, neuron network segmentation and more.