Abstract
Abstract In these notes we give an introduction to representation theory of simple finite-dimensional Lie superalgebras. We concentrate on so called basic superalgebras. Those are superalgebras which have even reductive part and admit an invariant form. We start with structure theory of basic superalgebras emphasizing abstract properties of roots and then proceed to representations, trying to demonstrate the variety of methods: Harish-Chandra homomorphism, support variety, translation functors, Borel-Weil-Bott theory and localization.
Notes
- 1.
A grading
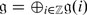 is compatible if
is compatible if 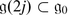 and
and 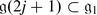 .
. - 2.
This assumption is not essential and can be dropped. It is here only for convenience of notations.
References
J. Brundan, Kazhdan-Lusztig polynomials and character formulae for the Lie superalgebra gl(m | n). J. Am. Math. Soc. 16(1), 185–231 (2003)
J. Brundan, C. Stroppel, Highest weight categories arising from Khovanov’s diagram algebra IV: the general linear supergroup. J. Eur. Math. Soc. 14(2), 373–419 (2012)
C. Carmeli, L. Caston, R. Fioresi, Mathematical Foundations of Supersymmetry. EMS Series of Lectures in Mathematics (EMS, Zurich, 2011)
S.J. Cheng, W. Wang, Dualities and Representations of Lie Superalgebras. Graduate Studies in Mathematics, vol. 144 (American Mathematical Society, Providence, RI, 2012)
S.J. Cheng, J.H. Kwon, Kac-Wakimoto character formula for ortho-symplectic Lie superalgebras (2017). arxiv:1406.6739
S.J. Cheng, N. Lam, W. Wang, Super duality for general linear Lie superalgebras and applications. Proc. Symposia Pure Math. Am. Math. Soc. 86, 113–136 (2012)
K. Coulembier, V. Serganova, Homological invariants in category O for the general linear superalgebra. Trans. Am. Math. Soc. (2017)
E. Dan-Cohen, I. Penkov, V. Serganova, A Koszul category of representations of finitary Lie algebras. Adv. Math. 289, 250–278 (2016)
P. Deligne, Catégories tannakiennes. The Grothendieck Festschrift (Birkhauser, Boston, 1990), pp. 111–195
J. Dixmier, Enveloping Algebras (Akademie-Verlag, Berlin, 1977)
M. Duflo, V. Serganova, On associated variety for Lie superalgebras (2005). arXiv: math/0507198
P. Gabriel, Indecomposable Representations II. Symposia Mathematica, vol. XI (Academic, London, 1973), pp. 81–104
J. Germoni, Representations indecomposables des algebres de Lie speciales lineaires. These de l’universite de Strasbourg (1997)
J. Germoni, Indecomposable representations of osp(3, 2), D(2, 1, a) and G 2, in Colloquium in Homology and Representation Theory, vol. 65, Bol. Acad. Nac. Cienc, Cordoba (2000), pp. 147–163
M. Gorelik, Strongly typical representations of the basic classical Lie superalgebras. J. Am. Math. Soc. 15(1), 167–184 (2002)
M. Gorelik, The Kac construction of the centre of
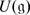 for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)
for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)C. Gruson, Sur l’ideal du cone autocommutant des super algebres de Lie basiques classiques et etranges. Ann. Inst. Fourier (Grenoble) 50(3), 807–831 (2000)
C. Gruson, Cohomologie des modules de dimension finie sur la super algebre
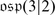 . J. Algebra 259, 581–598 (2003)
. J. Algebra 259, 581–598 (2003)C. Gruson, V. Serganova, Cohomology of generalized supergrassmannians and character formulae for basic classical Lie superalgebras. Proc. Lond. Math. Soc. (3) 101(3), 852–892 (2010)
C. Gruson, V. Serganova, Bernstein-Gelfand-Gelfand reciprocity and indecomposable projective modules for classical algebraic supergroups. Mosc. Math. J. 13(2), 281–313 (2013)
T. Heidersdorf, R. Wassauer, Cohomological tensor functors on representations of the general linear supergroup (2014). arXiv:1406.0321
V.G. Kac, Lie superalgebras. Adv. Math. 26, 8–96 (1977)
V.G. Kac, Representations of classical Lie superalgebras. Differential Geometrical Methods in Mathematical Physics, II. Proceedings of the Conference, University of Bonn, Bonn, 1977. Lecture Notes in Mathematics, vol. 676 (Springer, Berlin, 1978), pp. 597–626
V.G. Kac, Laplace operators of infinite-dimensional Lie algebras and theta functions. Proc. Nat. Acad. Sci. U. S. A. 81(2), 645–647 (1984). Phys. Sci.
V.G. Kac, M. Wakimoto, Integrable highest weight modules over affine superalgebras and number theory, in Lie Theory and Geometry. Progress in Mathematics, vol. 123 (Birkhäuser Boston, Boston, MA, 1994), pp. 415–456
M. Kontsevich, Defomation quantization of Poisson manifold. Lett. Math. Phys. 66(3), 157–216 (2003)
B. Kostant, Graded Manifolds, Graded Lie Theory, and Prequantization. Lecture Notes in Mathematics, vol. 570 (Springer, Berlin, 1977), pp. 177–306
J.L. Koszul, Graded manifolds and graded Lie algebras. International Meeting on Geometry and Physics (Bologna), Pitagora (1982), pp. 71–84
L. Martirosyan, The representation theory of the exceptional Lie superalgebras F(4) and G(3). J. Algebra 419, 167–222 (2014)
A. Masuoka, A. Zubkov, Quotient sheaves of algebraic supergroups are superschemes. J. Algebra 348, 135–170 (2011)
A. Masuoka, Harish-Chandra pairs for algebraic affine supergroup schemes over an arbitrary field. Transform. Groups 17(4), 1085–1121 (2012)
I. Musson, Lie Superalgebras and Enveloping Algebras. Graduate Studies in Mathematics, vol. 131 (American Mathematical Society, Providence, RI, 2012)
I. Musson, V. Serganova, Combinatorics of character formulas for the Lie superalgebra gl(m, n). Transform. Groups 16(2), 555–578 (2011)
A.L. Onishchik, E.B. Vinberg, Lie Groups and Algebraic Groups (Springer, Berlin, 1980)
I. Penkov, Borel-Weil-Bott theory for classical Lie supergroups. Translated in J. Soviet Math. 51(1), 2108–2140 (1990) [Russian]
I. Penkov, Characters of strongly generic irreducible Lie superalgebra representations. Internat. J. Math. 9(3), 331–366 (1998)
I. Penkov, K. Styrkas, Tensor representations of infinite-dimensional root-reductive Lie algebras, in Developments and Trends in Infinite-Dimensional Lie Theory, Progress in Mathematics, vol. 288 (Birkhäuser, Basel, 2011), pp. 127–150
S. Sam, A. Snowden, Stability patterns in representation theory. arXiv:1302.5859
V. Serganova, On generalized root systems. Commun. Algebra 24 (13), 4281–4299 (1996)
V. Serganova, Kazhdan-Lusztig polynomials and character formula for the Lie superalgebra gl(m | n). Selecta Math. (N.S.) 2(4), 607–651 (1996)
V. Serganova, A reduction method for atypical representations of classical Lie superalgebras. Adv. Math. 180, 248–274 (2003)
V. Serganova, On the superdimension of an irreducible representation of a basic classical Lie superalgebra, in Supersymmetry in Mathematics and Physics. Lecture Notes in Mathematics, vol. 2027 (Springer, Heidelberg, 2011), pp. 253–273
V. Serganova, Classical Lie superalgebras at infinity, in Advances in Lie Superalgebras. Springer INdAM Series, vol. 7 (Springer, Berlin, 2014), pp. 181–201
A. Sergeev, The tensor algebra of the tautological representation as a module over the Lie super-algebras gl(n, m) and Q(n). Mat. Sb. 123, 422–430 (1984) [in Russian]
A. Sergeev, The invariant polynomials on simple Lie superalgebras. Represent. Theory 3, 250–280 (1999)
E. Vishnyakova, On complex Lie supergroups and split homogeneous supermanifolds. Transform. Groups 16(1), 265–285 (2011)
Y.M. Zou, Categories of finite-dimensional weight modules over type I classical Lie superalgebras. J. Algebra 180, 459–482 (1996)
Acknowledgements
I thank the organizers of the workshop in Pisa for giving me the opportunity to give this minicourse and Rita Fioresi for writing the lecture notes. I thank the referee for pointing out numerous missprints in the first version of the paper. I also acknowledge partial support of NSF grant DMS-1303301.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Serganova, V. (2017). Representations of Lie Superalgebras. In: Callegaro, F., Carnovale, G., Caselli, F., De Concini, C., De Sole, A. (eds) Perspectives in Lie Theory. Springer INdAM Series, vol 19. Springer, Cham. https://doi.org/10.1007/978-3-319-58971-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-58971-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58970-1
Online ISBN: 978-3-319-58971-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


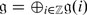 is compatible if
is compatible if 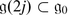 and
and 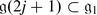 .
.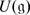 for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)
for Lie superalgebras. J. Nonlinear Math. Phys. 11(3), 325–349 (2004)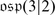 . J. Algebra 259, 581–598 (2003)
. J. Algebra 259, 581–598 (2003)