Keywords

1 Introduction

A tokamak is an experimental device whose purpose is to confine a plasma (ionized gas) in a magnetic field so as to control the nuclear fusion of atoms of low mass (deuterium, tritium,..) and to produce energy. The magnetic field has two components (see Fig. 1):

  • a toroidal field created by toroidal field coils, that is necessary for the stability of the plasma,

  • a poloidal field in the section of the torus created by poloidal field coils and by the plasma itself.

The plasma current is obtained by induction from currents in these poloidal field coils. The tokamak thus appears as a transformer whose plasma is the secondary. The currents in the external coils play another role, that of creating and controlling the equilibrium of the plasma. The goal of this paper is to provide a model for the evolution in time of the equilibrium of the plasma and to derive control methods in order to optimize a typical scenario of a discharge of the plasma in a tokamak.

Fig. 1.
figure 1

Schematic representation of a tokamak

Full size image

There are two approaches for simulating a plasma made of electrons and ions:

  • the microscopic approach based on kinetic equations (Vlasov, Boltzmann, Fokker-Planck) that are 6D (3D in space and 3D in terms of the velocity) and 1D in time.

  • the macroscopic approach based on magnetohydrodynamics (MHD) equations that are obtained by taking moments of the kinetic equations, and which are 3D in space and 1D in time. The validity of the MHD equations is clearly more restrictive than the one of the kinetic equations. We will present in Sect. 2 the way in which the MHD equations are obtained from the kinetic ones.

At the slow resistive diffusion time-scale, the plasma is in equilibrium at each instant (the kinetic pressure force balances at each point the Lorentz force due to the magnetic field) and hence the plasma follows the so-called quasi-static evolution of the equilibrium. The resistive diffusion in the external passive structures surrounding the plasma and the equations of the circuits of the poloidal field system enable to follow in time this quasi-static evolution. An axisymmetric hypothesis enables to reduce the problem to a 2D p.d.e. formulation, with the Grad-Shafranov equation for the equilibrium of the plasma. The plasma boundary is a free boundary, which is a particular poloidal flux line. It is either the outermost closed flux line inside the limiter, which prevents the plasma from touching the vacuum vessel, or a separatrix (with a hyperbolic X-point), as they are in presence of a poloidal divertor. This equilibrium model will be presented in Sect. 3 of the paper.

In order to solve numerically the set of equations for the poloidal flux, it is necessary to derive the weak formulation of this system and then a finite element method, coupled to Newton iterations for the treatment of the non-linearities, enables to solve the evolution of the equilibrium configuration in a tokamak. This is presented in Sect. 4 of this paper.

A typical discharge in a tokamak is made of several phases: ramp-up of total plasma current, plateau phase (stationary phase), ramp-down. The plasma shape can also move from a small circular plasma (at the beginning of the discharge) to a large elongated one with an X-point. The goal of this work is to determine, thanks to optimal control theory of systems governed by partial differential equations [1], the voltages applied to the poloidal field circuits that achieve at best the desired scenario, by minimizing a certain cost-function which represents the sum of the distance to the desired plasma and of the energetic cost of the electrical system. The introduction of an appropriate lagrangian taking as constraints the equilibrium system of the previous sections and the determination of the corresponding adjoint state enable the computation of the gradient of the cost-function in terms of the adjoint state. The minimization of this cost-function is performed thanks to a SQP (Sequential Quadratic Programming) method. An interesting test-case, solved by using these techniques, will be presented for the ITER (International Thermonuclear Experimental Reactor) tokamak. This is presented in Sect. 5 of this paper. This method has the purpose to replace the empirical methods used commonly to compute the pre-programmed voltages that enable to go from one snapshot to another one. This method can of course be extended to other type of optimization of the scenarios just by modifying the cost-function and the control variables (consumption of flux, desired profile of plasma current density,..).

2 The Magnetohydrodynamic Equations

A plasma is a ionized gas composed of ions and electrons. The kinetic equations describe the plasma thanks to a distribution function \(f_\alpha (\mathbf{x}, \mathbf{v},t)\) (with \(\alpha =e\) for electrons and \(\alpha =i\) for ions) where \(\mathbf{x}\) is the point position and \(\mathbf{v}\) the particles velocity. For a collisional plasma the kinetic equations are based on the Fokker-Planck equation

$$\begin{aligned} \frac{\partial f_\alpha }{\partial t}+ (\mathbf{v}.\nabla _\mathbf{x})f_\alpha +\frac{\mathbf{F}_\alpha }{m_\alpha }.\nabla _\mathbf{v} f_\alpha =C_\alpha , \end{aligned}$$
(1)

where \(m_\alpha \) is the mass of the particles, \(\mathbf{F}_\alpha \) the force applied to these particles and \(C_\alpha \) the term due to collisions between particles. This microscopic approach requires the resolution of a partial differential equations in 6 dimensions (space and velocity) plus the time dimension. This is extremely difficult from a computational point of view. Therefore from this equation one derives a macroscopic representation based on the fluid equations in the following way. Let us define the density of particles by

$$\begin{aligned} n_\alpha ({\varvec{x}},t)=\int f_\alpha ({\varvec{x}},{\varvec{w}},t)d{\varvec{w}}, \end{aligned}$$

the fluid velocity by

$$\begin{aligned} {\varvec{u}}_\alpha ({\varvec{x}},t)=\frac{1}{n_\alpha }\int f_\alpha ({\varvec{x}},{\varvec{w}},t){\varvec{w}}d{\varvec{w}}, \end{aligned}$$

and the pressure tensor

$$\begin{aligned} P_\alpha ({\varvec{x}},t)=m_\alpha \int f_\alpha ({\varvec{x}},{\varvec{w}},t)({\varvec{w}}-{\varvec{u}}_\alpha )({\varvec{w}}-{\varvec{u}}_\alpha )d{\varvec{w}}, \end{aligned}$$

which under the isotropic assumption becomes

$$\begin{aligned} p_\alpha ({\varvec{x}},t)=\frac{m_\alpha }{3}\int f_\alpha ({\varvec{x}},{\varvec{w}},t)({\varvec{w}}-{\varvec{u}}_\alpha )^2d{\varvec{w}}. \end{aligned}$$

Multiplying Eq. (1) by a test function \(\phi ({\varvec{w}})\) and integrating over the space of velocities leads to the fluid equations. The first moment (corresponding to \(\phi =1\)) gives the equation for the density of particles:

$$\begin{aligned} \frac{\partial n_\alpha }{\partial t}+\nabla .\int f_\alpha {\varvec{w}}d{\varvec{w}}-\frac{1}{m_\alpha }\int \frac{\partial {\varvec{F}}_\alpha }{\partial {\varvec{w}}}f_\alpha d{\varvec{w}}=0. \end{aligned}$$

Since for electromagnetic forces \(\displaystyle {\frac{\partial {\varvec{F}}_\alpha }{\partial {\varvec{w}}}=0}\), and since collisions do not change the number of particles one obtains:

$$\begin{aligned} \frac{\partial n_\alpha }{\partial t}+\nabla .(n_\alpha {\varvec{u}}_\alpha )=0. \end{aligned}$$

The second moment is obtained by taking \(\phi =m_\alpha {\varvec{w}}\) which leads to the momentum equation

$$\begin{aligned} m_\alpha \frac{\partial }{\partial t} (n_\alpha {\varvec{u}}_\alpha )+m_\alpha \nabla _x.\int f_\alpha {\varvec{w}}{\varvec{w}}d{\varvec{w}}-\int \nabla _{\varvec{w}}.({\varvec{F}}_\alpha .{\varvec{w}})f_\alpha d{\varvec{w}}=\int m_\alpha {\varvec{w}}C_\alpha d{\varvec{w}}, \end{aligned}$$

where we have set \(\displaystyle {{\varvec{w}}=({\varvec{w}}-{\varvec{u}}_\alpha )+{\varvec{u}}_\alpha }\). Using the equation for conservation of the density one gets

$$\begin{aligned} m_\alpha n_\alpha (\frac{\partial {\varvec{u}}_\alpha }{\partial t}+{\varvec{u}}_\alpha .\nabla {\varvec{u}}_\alpha )=-\nabla .P_\alpha +n_\alpha \overline{{\varvec{F}}_\alpha } +\mathbf{R_\alpha }, \end{aligned}$$

whith \(\overline{{\varvec{F}}_\alpha } = Ze ({\varvec{E}}+{\varvec{u}}_\alpha \times {\varvec{B}})\) where Ze is the charge of particles and \(\mathbf{R_\alpha }\) is the change rate of the momentum due to collisions.

The third moment gives the energy equation which needs to be complemented with closing relations on the heat flux. These latter come from a transport model. The single fluid magnetohydrodynamic equations are derived by defining the mass density

$$\begin{aligned} m n= & {} m_en_e+m_i n_i \\= & {} m_e Z{n_i}+m_in_i \approx m_i n_i \end{aligned}$$

the velocity of the fluid

$$\begin{aligned} {\varvec{u}}=\frac{m_e n_e {\varvec{u}}_e + m_i n_i {\varvec{u}}_i}{\rho }\approx {\varvec{u}}_i, \end{aligned}$$

the current density

$$\begin{aligned} {\varvec{j}}= & {} -e n_e {\varvec{u}}_e + Ze n_i{\varvec{u}}_i, \\= & {} e n_e ({\varvec{u}}_i - {\varvec{u}}_e), \end{aligned}$$

and the scalar pressure

$$\begin{aligned} p=n_e k T_e + n_i k T_i, \end{aligned}$$

where k is the Boltzmann constant. The Maxwell equations need to be added since we are in the presence of a magnetic field \({\varvec{B}}\) and of an electric field \({\varvec{E}}\). Finally the resistive MHD equations for a single fluid [2] read:

(2)

where n denotes the density of the particles, m their mass, \({\varvec{u}}\) their mean velocity, p their pressure, T their temperature, Q the heat flux, \(\eta \) the resistivity tensor, s and \(s'\) the source terms and k the Boltzmann constant.

3 Equilibrium of a Plasma in a Tokamak

In order to simplify system (2) some characteristic time constants of the plasma need to be defined. The Alfven time constant \(\tau _A\) is

$$\begin{aligned} \tau _A=\frac{a(\mu _0mn)^{1/2}}{B_0}, \end{aligned}$$

where a is the minor radius of the plasma and \({\varvec{B}}_0\) is the toroidal magnetic field. It is of the order of a microsecond for present tokamaks.

The diffusion time constant of the particle density n is

$$\begin{aligned} \tau _n=\frac{a^2}{D}, \end{aligned}$$

where D is the particle diffusion coefficient. Likewise, the time constants for diffusion of heat of the electrons and of the ions are

$$\begin{aligned} \tau _e=\frac{n_ea^2}{K_e}, \end{aligned}$$
$$\begin{aligned} \tau _i=\frac{n_ia^2}{K_i}, \end{aligned}$$

where \(n_e\), \(n_i\) are the density of electrons and ions, respectively, and \(K_e\), \(K_i\) are their thermal conductivities. These constants \(\tau _n\), \(\tau _e\), \(\tau _i\) are of the order of a millisecond on tokamaks currently operating.

Finally, the resistive time constant for the diffusion of the current density and magnetic field in the plasma is given by

$$\begin{aligned} \tau _r=\frac{\mu _0 a^2}{\eta }, \end{aligned}$$

and is of the order of a second.

If a global time constant for plasma diffusion is defined by

$$\begin{aligned} \tau _p=\inf (\tau _n,\tau _e,\tau _i,\tau _r), \end{aligned}$$

we note that

$$\begin{aligned} \tau _A\ll \tau _p. \end{aligned}$$

On the diffusion time-scale \(\tau _p\) the term (\(\frac{\partial u}{\partial t}+{\varvec{u}}\nabla {\varvec{u}}\)) is small compared with \(\nabla p \) (see [3, 4]) and the equilibrium equation

$$\begin{aligned} \nabla p={\varvec{j}}\times {\varvec{B}}\end{aligned}$$
(3)

is thus satisfied at every instant in the plasma.

Consequently the equations which govern the equilibrium of a plasma in the presence of a magnetic field in a tokamak are on the one hand Maxwell’s equations satisfied in the whole of space (including the plasma):

$$\begin{aligned} \left\{ \begin{array}{lll} \nabla \cdot {\varvec{B}}&{}=&{} 0, \\ \nabla \times (\displaystyle \frac{{\varvec{B}}}{\mu }) &{}=&{} {\varvec{j}}, \end{array} \right. \end{aligned}$$
(4)

and on the other hand the equilibrium Eq. (3) for the plasma itself.

Equation (3) means that the plasma is in equilibrium when the force \(\nabla p\) due the kinetic pressure p is equal to the Lorentz force of the magnetic pressure \({\varvec{j}}\times {\varvec{B}}\). We deduce immediately from (3) that

$$\begin{aligned} {\varvec{B}}\cdot \nabla p = 0, \end{aligned}$$
(5)

and

$$\begin{aligned} {\varvec{j}}\cdot \nabla p = 0. \end{aligned}$$
(6)

Thus for a plasma in equilibrium the field lines and the current lines lie on isobaric surfaces (\(p=const.\)); these surfaces, generated by the field lines, are called magnetic surfaces. In order for them to remain within a bounded volume of space it is necessary that they have a toroidal topology. These surfaces form a family of nested tori. The innermost torus degenerates into a curve which is called the magnetic axis.

In a cylindrical coordinate system \((r,\phi ,z)\) (where \(r=0\) is the major axis of the torus) the hypothesis of axial symmetry consists in assuming that the magnetic field \({\varvec{B}}\) is independent of the toroidal angle \(\phi \). The magnetic field can be decomposed as \({\varvec{B}}={\varvec{B}}_p +{\varvec{B}}_{\phi }\), where \({\varvec{B}}_p=(B_r,B_z)\) is the poloidal component and \({\varvec{B}}_{\phi }\) is the toroidal component. From Eq. (4) one can define the poloidal flux \(\psi (r,z)\) such that

$$\begin{aligned} \left\{ \begin{array}{lll} B_r &{}=&{}-\displaystyle \frac{1}{r}\frac{\partial \psi }{\partial z}, \\ B_z &{}= &{} \displaystyle \frac{1}{r}\frac{\partial \psi }{\partial r}. \end{array} \right. \end{aligned}$$
(7)

Concerning the toroidal component \({\varvec{B}}_{\phi }\) we define f by

$$\begin{aligned} {\varvec{B}}_{\phi }=\frac{f}{r}{\varvec{e}}_{\phi }, \end{aligned}$$
(8)

where \({\varvec{e}}_{\phi }\) is the unit vector in the toroidal direction, and f is the diamagnetic function. The magnetic field can be written as:

$$\begin{aligned} \left\{ \begin{array}{lll} {\varvec{B}}&{}=&{}{\varvec{B}}_p+{\varvec{B}}_{\phi }, \\ {\varvec{B}}_p &{}=&{}\displaystyle \frac{1}{r}[\nabla \psi \times {\varvec{e}}_{\phi }], \\ {\varvec{B}}_{\phi } &{}= &{} \displaystyle \frac{f}{r} {\varvec{e}}_{\phi }. \end{array} \right. \end{aligned}$$
(9)

According to (9), in an axisymmetric configuration the magnetic surfaces are generated by the rotation of the flux lines \(\psi =const.\) around the axis \(r=0\) of the torus.

From (9) and the second relation of (4) we obtain the following expression for \({\varvec{j}}\):

$$\begin{aligned} \left\{ \begin{array}{lll} {\varvec{j}}&{}=&{}{\varvec{j}}_p+{\varvec{j}}_{\phi },\\ {\varvec{j}}_p &{}=&{}\displaystyle \frac{1}{r}[\nabla (\frac{f}{\mu }) \times {\varvec{e}}_{\phi }], \\ {\varvec{j}}_{\phi } &{}= &{} (-\varDelta ^* \psi ) {\varvec{e}}_{\phi } , \end{array} \right. \end{aligned}$$
(10)

where \({\varvec{j}}_p\) and \({\varvec{j}}_{\phi }\) are the poloidal and toroidal components respectively of \({\varvec{j}}\), and the operator \(\varDelta ^*\) is defined by

$$\begin{aligned} \varDelta ^* \cdot = \partial _r\left( \frac{1}{\mu r} \partial _r \cdot \right) + \partial _z\left( \frac{1}{\mu r} \partial _z \cdot \right) =\nabla \left( \frac{1}{\mu r} \nabla \cdot \right) . \end{aligned}$$
(11)

Expressions (9) and (10) for \({\varvec{B}}\) and \({\varvec{j}}\) are valid in the whole of space since they involve only Maxwell’s equations and the hypothesis of axisymmetry. Hence they can be reduced to one equation given in 2 space dimensions in the poloidal plane \((r,z) \in \varOmega _{\infty }=(0,\infty ) \times (-\infty ,\infty )\) for the poloidal flux \(\psi \):

$$\begin{aligned} - \varDelta ^* \psi = j_\phi . \end{aligned}$$
(12)
Fig. 2.
figure 2

Schematic representation of the poloidal plane of a tokamak. \(\varOmega _{\mathrm p}\) is the plasma domain, \(\varOmega _{\mathrm L}\) is the limiter domain accessible to the plasma, \(\varOmega _{\mathrm c_{i}}\) represent poloidal field coils, \(\varOmega _{\mathrm {ps}}\) the passive structures and \(\varOmega _{\mathrm {Fe}}\) the ferromagnetic structures.

Full size image
Fig. 3.
figure 3

Example of a plasma whose boundary is defined by the contact with limiter (left) or by the presence of an X-point (right).

Full size image

The toroidal component of the current density \(j_\phi \) is zero everywhere outside the plasma domain, the poloidal field coils and the passive structures. The different sub-domains of the poloidal plane of a tokamak (see Fig. 2) as well as the corresponding expression for \(j_\phi \) are described below:

  • \(\varOmega _{\mathrm L}\) is the domain accessible to the plasma. Its boundary is the limiter \(\partial \varOmega _{\mathrm L}\).

  • \(\varOmega _{\mathrm p}\) is the plasma domain where relation (5) implies that \(\nabla p\) and \(\nabla \psi \) are co-linear, and therefore p is constant on each magnetic surface. This can be denoted by

    $$\begin{aligned} p=p(\psi ). \end{aligned}$$
    (13)

    Relation (6) combined with the expression (10) implies that \(\nabla f\) and \(\nabla p\) are co-linear, and therefore f is likewise constant on each magnetic surface

    $$\begin{aligned} f=f(\psi ). \end{aligned}$$
    (14)

    The equilibrium relation (3) combined with the expression (9) and (10) for B and j implies that:

    $$\begin{aligned} \nabla p = - \displaystyle \frac{\varDelta ^* \psi }{r} \nabla \psi - \frac{f}{\mu _0 r^2} \nabla f, \end{aligned}$$
    (15)

    which leads to the so-called Grad-Shafranov equilibrium equation:

    $$\begin{aligned} -\varDelta ^* \psi = r p'(\psi ) + \frac{1}{\mu _0 r}(ff')(\psi ). \end{aligned}$$
    (16)

    Here \(\mu \) is equal to the magnetic permeability \(\mu _0\) of the vacuum and \(\varDelta ^*\) is a linear elliptic operator. From (10) it is clear that right-hand side of (16) represents the toroidal component of the plasma current density. It involves functions \(p(\psi )\) and \(f(\psi )\) which are not directly measured inside the plasma. The plasma domain is unknown, \(\varOmega _{\mathrm p}=\varOmega _{\mathrm p}(\psi )\), and this is a free boundary problem. This domain is defined by its boundary which is the largest closed \(\psi \) iso-contour contained within the limiter \(\varOmega _{\mathrm L}\). The plasma can either be limited if this iso-contour is tangent to the limiter \(\partial \varOmega _{\mathrm L}\) (see Fig. 3, left) or defined by the presence of a saddle-point also called X-point (see Fig. 3, right). In the later configuration which is obtained in presence of a divertor, the plasma does not touch any physical component and the performances and the confinement of the plasma are improved (see [5]).

  • \(\varOmega _{\mathrm {Fe}}\) represents the ferromagnetic structures. They do not carry any current, \(j_\phi = 0\) but the magnetic permeability \(\mu \) is not constant and depends on the magnetic field:

    $$\begin{aligned} \mu = \mu _\mathrm {Fe}(\frac{|\nabla \psi |^2}{r^2}). \end{aligned}$$
    (17)

  • Domains \(\varOmega _{\mathrm c_{i}}\) represent the poloidal field coils carrying currents. If we consider that the voltages \(V_i\) applied to these coils are given, using Faraday and Ohm laws the current density can be written as

    $$\begin{aligned} j_\phi =\displaystyle \frac{n_i V_i}{R_i |\varOmega _{\mathrm c_{i}}|} - \frac{2\pi n_i^2}{R_i |\varOmega _{\mathrm c_{i}}|^2} \int _{\varOmega _{C_i}} \dot{\psi } ds, \end{aligned}$$
    (18)

    where \(n_i\) is the number of windings in the coil, \(|\varOmega _{\mathrm c_{i}}|\) its section area, \(R_i\) its resistance and \(\dot{\psi }\) is the time derivative of \(\psi \),

  • \(\varOmega _{\mathrm {ps}}\) represents passive structures where the current density can be written as

    $$\begin{aligned} j_\phi =- \displaystyle \frac{\sigma }{r}\dot{\psi }, \end{aligned}$$
    (19)

    where \(\sigma \) is the conductivity.

In summary we are seeking for the poloidal flux \(\psi (t)\) that is a solution of (12) with \(j_\phi \) given by (16), (18) and (19) and verifies boundary conditions

$$\begin{aligned} \psi (0,z)=0\quad \mathrm {and}\quad \lim \limits _{\Vert (r,z)\Vert \rightarrow +\infty } \psi (r,z)= 0. \end{aligned}$$

4 Weak Formulation and Discretization

We chose a semi-circle \(\varGamma \) of radius \(\rho _\varGamma \) surrounding the iron domain \(\varOmega _{\mathrm {Fe}}\), the coil domains \(\varOmega _{\mathrm c_{i}}\) and the passive structures domain \(\varOmega _{\mathrm {ps}}\). The truncated domain, we use for our computations, is the domain \(\varOmega \) having the boundary \(\partial \varOmega = \varGamma \cup \varGamma _{0}\), where \(\varGamma _{0}:=\{(0,z),\, z_{min}\le z \le z_{max}\}\). The weak formulation for \(\psi (t)\) uses the following Sobolev space:

$$\begin{aligned} H:= \left\{ \psi : \varOmega \rightarrow \mathbb R, \Vert \psi \Vert< \infty , \Vert \frac{|\nabla \psi |}{r}\Vert < \infty , \, \psi _{|\varGamma _0} = 0 \right\} \cap C^0(\overline{\varOmega }), \end{aligned}$$

with

$$ \Vert \psi \Vert ^2 = \int _{\varOmega } \psi ^2 \, r\, dr dz. $$

It reads as: Given \(\mathbf V(t) = \{V_i(t)\}_{i=1}^N\) find \(\psi (t) \in H \) such that for all \(\xi \in H\)

$$\begin{aligned} \mathsf {A}(\psi (t),\xi ) - \,\mathsf {J}_{\mathrm p}(\psi (t),\xi ) + \mathsf {j}^{\mathrm {ps}}(\dot{\psi }(t),\xi ) + \mathsf {j}^{\mathrm {c}}(\dot{\psi }(t),\xi ) + \mathsf {c}(\psi (t),\xi ) = \mathsf {\ell }(\mathbf V(t),\xi ), \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{aligned} \mathsf {A}(\psi ,\xi )&:= \int _{\varOmega } \frac{1}{\mu (\psi ) r} \nabla \psi \cdot \nabla \xi \, dr dz, \\ \mathsf {J}_{\mathrm p}(\psi ,\xi )&:= \int _{\varOmega _{\mathrm p}(\psi )} \left( r S_{p'}(\psi _{\mathrm N}) + \frac{1}{\mu _0 r} S_{ff'}(\psi _{\mathrm N}) \right) \xi \, dr dz,\\ \mathsf {\ell }(\mathbf V(t),\xi )&:= \sum _{i=1}^N \frac{n_i}{R_i|\varOmega _{\mathrm c_{i}}|} V_i(t) \int _{\varOmega _{\mathrm c_{i}}} \xi \, dr dz, \\ \mathsf {j}^{\mathrm {ps}}(\psi ,\xi )&:= \int _{\varOmega _{\mathrm {ps}}} \frac{\sigma }{r} \psi \xi \, dr dz,\\ \mathsf {j}^{\mathrm c}(\psi ,\xi )&:= \sum _{i=1}^{N_i} \frac{ 2 \pi n_i^2}{R_i |\varOmega _{\mathrm c_{i}}|^2} \int _{\varOmega _{\mathrm c_{i}}} \psi \, dr dz \int _{\varOmega _{\mathrm c_{i}}} \xi \, dr dz, \\ \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} \mathsf {c}(\psi ,\xi )&:= \frac{1}{\mu _0}\int _\varGamma \psi (\mathbf {P}_1) N(\mathbf {P}_1) \xi (\mathbf {P}_1) dS_1 \nonumber \\&+ \frac{1}{2 \mu _0}\int _\varGamma \int _\varGamma (\psi (\mathbf {P}_1)-\psi (\mathbf {P}_2)) M(\mathbf {P}_1,\mathbf {P}_2) (\xi (\mathbf {P}_1)-\xi (\mathbf {P}_2)) dS_1 dS_2, \end{aligned}$$
(22)

with

$$\begin{aligned} \begin{array}{ll} M(\mathbf {P}_1,\mathbf {P}_2) &{} = \frac{k_{\mathbf {P}_1,\mathbf {P}_2}}{2 \pi (r_1 r_2)^\frac{3}{2}} \left( \frac{2-k_{\mathbf {P}_1,\mathbf {P}_2}^2}{2-2k_{\mathbf {P}_1,\mathbf {P}_2}^2} E(k_{\mathbf {P}_1,\mathbf {P}_2})-K(k_{\mathbf {P}_1,\mathbf {P}_2})\right) , \\ N(\mathbf {P}_1) &{} = \frac{1}{r_1}\left( \frac{1}{\delta _+}+\frac{1}{\delta _-} -\frac{1}{\rho _\varGamma }\right) \text { and } \delta _\pm = \sqrt{r_1^2 + ( \rho _\varGamma \pm z_1 )^2}. \end{array} \end{aligned}$$

where \(\mathbf {P}_i = (r_i,z_i)\) and K and E the complete elliptic integrals of first and second kind, respectively and

$$\begin{aligned} k_{\mathbf {P}_j,\mathbf {P}_k} = \sqrt{\frac{4 r_j r_k}{(r_j+r_k)^2 + (z_j-z_k)^2}}. \end{aligned}$$

The bilinear form \(\mathsf {c}: H \times H\rightarrow \mathbb R\) is accounting for the boundary conditions at infinity [6]. We refer to [7, Chap. 2.4] for the details of the derivation. The bilinear form \(\mathsf {c}(\cdot ,\cdot )\) follows basically from the so-called uncoupling procedure in [8] for the usual coupling of boundary integral and finite element methods. As we focus here on the equilibrium problem the two functions \(p'\) and \(f\,f'\) have to be supplied as data, called \(S_{p'}\) and \(S_{ff'}\) in the definition of \(\mathsf {J}_{\mathrm p}(\psi ,\xi )\). While the domain of \(p'\) and \(f\,f'\) depends on the poloidal flux itself, it is more practical to supply those profiles \(S_{p'}\) and \(S_{ff'}\) as functions of the normalized poloidal flux \(\psi _\mathrm {N}(r,z)\):

$$\begin{aligned} \psi _\mathrm {N}(r,z) = \frac{\psi (r,z) - \psi _{\mathrm {ax}}(\psi )}{\psi _{\mathrm {bd}}(\psi ) - \psi _{\mathrm {ax}}(\psi )}, \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{aligned} \psi _{\mathrm {ax}}(\psi )&:=\psi (r_{\mathrm {ax}}(\psi ),z_{\mathrm {ax}}(\psi )), \\ \psi _{\mathrm {bnd}}(\psi )&:= \psi (r_{\mathrm {bd}}(\psi ),z_{\mathrm {bd}}(\psi )) \end{aligned} \end{aligned}$$
(24)

with \((r_{\mathrm {ax}}(\psi ),z_{\mathrm {ax}}(\psi ))\) the magnetic axis, where \(\psi \) has its global maximum in \(\varOmega _{\mathrm L}\) and \((r_{\mathrm {bnd}}(\psi ),z_{\mathrm {bnd}}(\psi ))\) the coordinates of the point that determines the plasma boundary. The point \((r_{\mathrm {bnd}},z_{\mathrm {bnd}})\) is either an X-point of \(\psi \) or the contact point with the limiter \(\partial \varOmega _{\mathrm L}\). \(S_{p'}\) and \(S_{ff'}\), have, independently of \(\psi \), a fixed domain [0, 1] and are usually given as (piecewise) polynomial functions. Another frequent a priori model is

$$\begin{aligned} \begin{array}{lll} S_{p'}(\psi _{\mathrm N})&= \displaystyle \lambda \frac{\beta }{r_0} (1-\psi _{\mathrm {N}}^\alpha )^\gamma \,,\quad S_{ff'}(\psi _{\mathrm N})&= \lambda (1-\beta )\mu _0 r_0(1-\psi _{\mathrm {N}}^\alpha )^\gamma \end{array} \end{aligned}$$
(25)

with \(r_0\) the major radius of the vacuum chamber and \(\alpha ,\beta ,\gamma \in {\mathbb R}\) given parameters. We refer to [9] for a physical interpretation of these parameters. The parameter \(\beta \) is related to the poloidal beta, whereas \(\alpha \) and \(\gamma \) describe the peakage of the current profile and \(\lambda \) is a normalization factor.

Numerical Methods. It is straightforward to combine Galerkin methods in space and time-stepping schemes to get approximation schemes for solving (20) numerically. For the choice of the spatial discretization, the fine details of realistic tokamak sections (see Fig. 4) give here favor to finite element spaces based on triangular meshes. Since for many years now the piecewise affine approximations are the standard choice for the stationary free-boundary equilibrium problems [7, 10, 11], we stay also here with linear Lagrangian finite elements for the discretization in space. Higher order methods are likewise implementable.

Fig. 4.
figure 4

The different subdomains of the geometry of the tokamak WEST (left) and ITER (right) and triangulations that resolve the geometric details.

Full size image

In order to prohibit numerical instablities it is advisable to use implicit time-stepping methods such as implicit Euler, which leads to non-linear finite-dimensional problems. The Newton-type methods for solving such non-linear problems can be based on the Gâteaux derivative

$$\begin{aligned} D_{\psi } \mathsf {A}(\psi ,\xi )(\tilde{\psi }) = \int _{\varOmega } \frac{1}{\mu (\psi ) r} \nabla&\tilde{\psi }\cdot \nabla \xi \, dr dz \\&-2 \int _{\varOmega _{\mathrm {Fe}}} \frac{\mu _{\mathrm {Fe}}'(\frac{|\nabla \psi |^2}{r^{2}})}{\mu _{\mathrm {Fe}}^2(\frac{|\nabla \psi |^2}{r^{2}}) r^3} (\nabla \tilde{\psi }\cdot \nabla \psi ) (\nabla \psi \cdot \nabla \xi ) \, dr dz \end{aligned}$$

of \(\mathsf {A}(\psi ,\xi )\) and the Gâteaux derivative

$$\begin{aligned} \begin{aligned} D_{\psi }\mathsf {J}_{\mathrm p}(\psi , \xi )(\widetilde{\psi })=&\int _{\varOmega _{\mathrm p}(\psi )} \frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi ))}{\partial \psi _{\mathrm N}}\frac{\partial \psi _{\mathrm N}(\psi )}{\partial \psi } \widetilde{\psi }\, \xi \, dr dz \\&- \int _{\varGamma _{\mathrm p}(\psi )} j_{\mathrm p}(r,1) |\nabla \psi |^{-1} (\widetilde{\psi }-\widetilde{\psi }(r_{\mathrm {bd}}(\psi ),z_{\mathrm {bd}}(\psi ))) \xi \, d\varGamma \\&+ \int _{\varOmega _{\mathrm p}(\psi )} \frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi )) }{\partial \psi _{\mathrm N}} \frac{\partial \psi _\mathrm {N}(\psi )}{\partial \psi _{\mathrm {ax}}} \widetilde{\psi }(r_{\mathrm {ax}}(\psi ),z_{\mathrm {ax}}(\psi )) \xi \, dr dz \\&+ \int _{\varOmega _{\mathrm p}(\psi )}\frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi ))}{\partial \psi _{\mathrm N}}\frac{\partial \psi _\mathrm {N}(\psi )}{\partial \psi _{\mathrm {bd}}} \widetilde{\psi }(r_{\mathrm {bd}}(\psi ),z_{\mathrm {bd}}(\psi )) \xi \, dr dz \end{aligned} \end{aligned}$$
(26)

of \(\mathsf {J}_{\mathrm p}(\psi ,\xi )\), where \(\varGamma _{\mathrm p}\) is the plasma boundary \( \partial \varOmega _{\mathrm p}\) and

$$\begin{aligned} j_{\mathrm p}(r,\psi _{\mathrm N}(\psi )) =r S_{p'}(\psi _{\mathrm N}(\psi )) + \frac{1}{\mu _0 r} S_{ff'}(\psi _{\mathrm N}(\psi )). \end{aligned}$$
(27)

The derivation of the linearization \( D_{\psi }\mathsf {J}_{\mathrm p}(\psi , \xi )(\widetilde{\psi })\) requires to assume that \(\nabla \psi \ne 0 \) on \(\partial \varOmega _{\mathrm p}\) and involves shape calculus [12, 13] and the non-trivial derivatives:

$$\begin{aligned} D_{\psi } \psi _{\mathrm {ax}}(\psi )(\tilde{\psi }) = \tilde{\psi }(r_{\mathrm {ax}}(\psi ),z_{\mathrm {ax}}(\psi )) \text { and } D_{\psi } \psi _{\mathrm {bd}}(\psi )(\tilde{\psi }) = \tilde{\psi }(r_{\mathrm {bd}}(\psi ), z_{\mathrm {bd}}(\psi )). \end{aligned}$$

Clearly, \(\nabla \psi \ne 0 \) on \(\partial \varOmega _{\mathrm p}\) will not be true for the nowadays important X-point equilibria. Nevertheless this theoretical difficulty is not very essential for practical computations. In [14] it is pointed out that accurate Newton methods for discretized versions of the weak formulation (20) need to use accurate derivatives for the discretized non-linear operator, which is not necessarily equal to the discretization of the analytical derivatives. Here, the discretization and linearization of \(\mathsf {J}_{\mathrm p}(\psi , \xi )\) needs special attention due to the \(\psi \)-dependent domain of integration. We refer to [14, Sect. 3.2] and [14, Sect. 3.3] for the technical details.

5 The Optimal Control Problem

We intend to determine the voltages \(V_i(t)\) applied to the poloidal field circuits so that the plasma boundary \(\varGamma _\mathrm {p}\) fit to a desired boundary \(\varGamma _\mathrm {desi}\) during the whole discharge while minimizing a certain energetic cost.

Let \(\varGamma _{\mathrm {desi}}(t) \subset \varOmega _{\mathrm L}\) denote the evolution of a closed line, contained in the domain \(\varOmega _{\mathrm L}\) that is either smooth and touches the limiter at one point or has at least one corner. The former case prescribes a desired plasma boundary that touches the limiter. The latter case aims at a plasma with X-point that is entirely in the interior of \(\varOmega _{\mathrm L}\). Further let \((r_{\mathrm {desi}}(t),z_{\mathrm {desi}}(t)) \in \varGamma _{\mathrm {desi}}(t)\) and \((r_{1}(t),z_{1}(t)),\dots ,(r_{N_{\mathrm {desi}}}(t),z_{N_{\mathrm {desi}}}(t))\in \varGamma _{\mathrm {desi}}(t)\) be \(N_{\mathrm {desi}}+1\) points on that line. We define a quadratic functional \(K(\psi )\) that evaluates to zero if \(\varGamma _{\mathrm {desi}}(t)\) is an \(\psi (t)\)-isoline, i.e. if \(\psi (t)\) is constant on \(\varGamma _{\mathrm {desi}}(t)\):

$$\begin{aligned} K(\psi ,t):=\frac{1}{2} \left( \sum _{i=1}^{N_{\mathrm {desi}}} \big (\psi (r_i(t),z_i(t))-\psi (r_{\mathrm {desi}}(t),z_{ \mathrm { desi } }(t))\big )^2 \right) . \end{aligned}$$
(28)

Another functional, that will serve as regularization, is

$$\begin{aligned} R(\mathbf V(t)):=\sum _{i=1}^N \frac{w_i}{2} \mathbf V^2_i \end{aligned}$$
(29)

with regularization weights \(w_i\ge 0\). The regularization functional penalizes the strength of the voltages \(V_i\) and represents the energetic cost in the coil system.

We consider the following minimization problem:

$$\begin{aligned} \min _{\psi (t),\mathbf V(t)} \int _0^T K(\psi (t),t)+R( \mathbf V(t)) \, dt \end{aligned}$$
(30)

subject to

$$ \mathsf {A}(\psi (t),\xi ) - \,\mathsf {J}_{\mathrm p}(\psi (t),\xi ) + \mathsf {j}^{\mathrm {ps}}(\dot{\psi }(t),\xi )+ \mathsf {j}^{\mathrm {c}}(\dot{\psi }(t),\xi ) + \mathsf {c}(\psi (t),\xi ) = \mathsf {\ell }(\mathbf V(t),\xi ) \quad \forall \xi \in H. $$

This minimization problem for transient axisymmetric equilibria extends the minimization problems for static axisysmmetric equilibria introduced in [15, Chap. II]. Hence, theoretical assertions for (30) such as the first order necessary conditions for optimality follow by similar arguments as those in [15, p. 80–84].

The Lagrangian for the optimization problem (30) with Lagrange multiplier \(\phi \) is:

$$\begin{aligned} \begin{aligned} \mathcal L(\psi (t),\mathbf V(t),\phi (t)) =&\int _0^T K(\psi (t),t) + R(\mathbf V(t)) \, dt \\&- \int _0^T \mathsf {A}(\psi (t),\phi (t)) - \,\mathsf {J}_{\mathrm p}(\psi (t),\phi (t)) + \mathsf {c}(\psi (t),\phi (t)) dt \\&- \int _0^T\mathsf {j}^{\mathrm {ps}}(\dot{\psi }(t),\phi (t)) + \mathsf {j}^{\mathrm {c}}(\dot{\psi }(t),\phi (t)) - \mathsf {\ell }(\mathbf V(t),\phi (t)) dt. \end{aligned} \end{aligned}$$

We can state the first order necessary conditions for optimality under the following three assumptions in the limiter case:

  1. 1.

    \(\sup _{\varOmega _{\mathrm L}} \psi \) is attained at one and only one point \(\mathbf M_0 = (r_\mathrm {bd},z_\mathrm {bd})\).

  2. 2.

    \(\sup _{\varOmega _{\mathrm p}} \psi \) is attained at one and only one point \(\mathbf M_1\), which is an interior point of \(\varOmega _{\mathrm p}\) and \(\mathbf M_1 = (r_\mathrm {ax},z_\mathrm {ax})\). \(\psi \) is of class \(C^2\) in a neighbourhood of \(\mathbf M_1\) and the point \(\mathbf M_1\) is a non-degenerated elliptic point.

  3. 3.

    \(\nabla \psi \) vanishes nowhere on \(\partial \varOmega _{\mathrm p}\).

Equivalent necessary conditions can be obtained in the X-point case.

Then necessary conditions for \((\psi (t),\mathbf V(t),\phi (t))\) to be a saddle point of \(\mathcal L\) are obtained, after integrating by parts in time the Lagrangian:

  • \(\psi (t)\) and \(\mathbf V(t)\) are solution of the direct problem (20)

  • \(\psi (t)\) and \(\phi (t)\) are solution of the adjoint problem

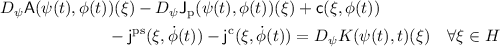    (31)

    with \(\phi (T) = 0\) and

    $$\begin{aligned} D_\psi K(\psi ,t)(\xi ) = \sum _{i=1}^{N_{\mathrm {desi}}} \big (\psi (r_i(t),z_i(t))&-\psi (r_{\mathrm {desi}}(t),z_{ \mathrm { desi } }(t))\big ) \cdot \\&\big (\xi (r_i(t),z_i(t))-\xi (r_{\mathrm {desi}}(t),z_{ \mathrm { desi } }(t))\big ). \end{aligned}$$

  • \(\mathbf V(t)\) and \(\phi (t)\) are solution to

    $$\begin{aligned} {w_i} V_i(t) + \frac{n_i}{R_i|\varOmega _{\mathrm c_{i}}|} \int _{\varOmega _{\mathrm c_{i}}} \phi (t) \, dr dz =0\,, \quad 1 \le i \le N. \end{aligned}$$
    (32)

The adjoint problem has the following strong formulation:

$$\begin{aligned} -\varDelta ^* \phi (t) +&1_{\varOmega _{\mathrm {Fe}}} \nabla \cdot \left( 2 \frac{\mu _{\mathrm {Fe}}'(\frac{|\nabla \psi |^2}{r^{2}})}{\mu _{\mathrm {Fe}}^2(\frac{|\nabla \psi |^2}{r^{2}}) r^3} (\nabla \phi (t)\cdot \nabla \psi ) \nabla \psi \right) \\&- 1_{\varOmega _{\mathrm p}(\psi )} \frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi ))}{\partial \psi _{\mathrm N}}\frac{\partial \psi _{\mathrm N}(\psi )}{\partial \psi } \phi (t) \\&- \delta _\mathrm {bd} \int _{\varGamma _{\mathrm p}(\psi )} \frac{j_{\mathrm p}(r,1)}{|\nabla \psi |} \phi (t) \, d\varGamma + (\delta _{\varGamma _\mathrm {p}}, \frac{j_{\mathrm p}(r,1)}{|\nabla \psi |} \phi (t))\\&- \delta _\mathrm {ax} \int _{\varOmega _{\mathrm p}(\psi )} \frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi )) }{\partial \psi _{\mathrm N}} \frac{\partial \psi _\mathrm {N}(\psi )}{\partial \psi _{\mathrm {ax}}} \phi (t) \, dr dz \\&- \delta _\mathrm {bd} \int _{\varOmega _{\mathrm p}(\psi )} \frac{\partial j_{\mathrm p} (r,\psi _{\mathrm N}(\psi ))}{\partial \psi _{\mathrm N}}\frac{\partial \psi _\mathrm {N}(\psi )}{\partial \psi _{\mathrm {bd}}} \phi (t) \, dr dz \\&- 1_{\varOmega _{\mathrm {ps}}} \frac{\sigma }{r} \dot{\phi }(t) - \sum _{i=1}^{N_i} 1_{\varOmega _{\mathrm c_{i}}} \frac{ 2 \pi n_i^2}{R_i |\varOmega _{\mathrm c_{i}}|^2} \int _{\varOmega _{\mathrm c_{i}}} \dot{\phi }\, dr dz \\& = \left( \sum _{i=1}^{N_{\mathrm {desi}}} \big (\psi (r_i(t),z_i(t),t)-\psi (r_{\mathrm {desi}}(t),z_{ \mathrm { desi } }(t),t)\big ) \right) \left( \delta _{(r_i,z_i)}-\delta _{(r_{\mathrm {desi}},z_{ \mathrm { desi } })}\right) \end{aligned}$$

with \(\phi (T)=0\), where \(\delta _\mathrm {ax}\) and \(\delta _\mathrm {bd}\) are the Dirac masses at the points \((r_\mathrm {ax},r_\mathrm {ax})\) and \((r_\mathrm {bd},r_\mathrm {bd})\), respectively. \(\delta _{\varGamma _{\mathrm {p}}}\) is the Dirac mass of \(\varGamma _\mathrm {p}\) with

$$ (\delta _{\varGamma _\mathrm {p}}, \frac{j_{\mathrm p}(r,1)}{|\nabla \psi |} \phi (t) \xi ) = \int _{\varGamma _\mathrm {p}} \frac{j_{\mathrm p}(r,1)}{|\nabla \psi |} \phi (t) \xi \, d\varGamma . $$

Equation (32) is the Euler equation for the minimization of (30). Equations (20), (31) and (32) constitute the optimality system for problem (30).

Numerical Methods. The discretization of our minimization problem (30) builds on the space-time discretization for (20) that we outlined in the previous section. Next, the discrete minimization problem can be recast as the following constrained optimization problem

$$\begin{aligned} \begin{aligned} \min _{\mathbf u, \mathbf y} J(\mathbf y,\mathbf u)&\quad \text {s.t.}\quad \mathbf B(\mathbf y) =\mathbf F(\mathbf u), \end{aligned} \end{aligned}$$
(33)

where \(\mathbf y\) and \(\mathbf u\) are the so-called state and control variables. In our setting \(\mathbf y\) will be the variable that describes the plasma and \(\mathbf u\) will be the externally applied voltages. We think of \(\mathbf y\) as the vector of degrees of freedoms describing the space and time evolution of the poloidal flux \(\psi \), and \(\mathbf B(\mathbf y)\) and \(\mathbf F(\mathbf u)\) are the discretizations of the non-linear operators in the variational formulation (20). Sequential Quadratic Programming (SQP) is one of the most effective methods for non-linear constrained optimization with significant non-linearities in the constraints [16, Chap. 18]. SQP methods find a numerical solution by generating iteration steps that minimize quadratic cost functions subject to linear constraints. The Lagrange function formalism in combination with Newton-type iterations is one approach to derive the SQP-methods: the Lagrangian for (33) is

$$\begin{aligned} L(\mathbf y,\mathbf u,\mathbf p) = J(\mathbf y, \mathbf u) + \langle \mathbf p, \mathbf B(\mathbf y) - \mathbf F(\mathbf u) \rangle , \end{aligned}$$
(34)

and the solution of (33) is a stationary point of this Lagrangian:

$$\begin{aligned} \begin{array}{rcl} D_\mathbf yJ(\mathbf y,\mathbf u) + D_\mathbf y\mathbf B^T(\mathbf y) \mathbf p&{}\,=\,&{} 0, \\ D_\mathbf uJ(\mathbf y,\mathbf u) - D_\mathbf u\mathbf F^T(\mathbf u) \mathbf p&{}\,=\,&{} 0, \\ \mathbf B(\mathbf y) - \mathbf F(\mathbf u) &{}\,=\,&{}0. \end{array} \end{aligned}$$
(35)

A Newton-type method for solving (35) are iterations of the type

$$\begin{aligned} \begin{pmatrix} \mathbf H_{\mathbf y,\mathbf y}^k &{} \mathbf H_{\mathbf y,\mathbf u}^k &{} D_\mathbf y\mathbf B^T(\mathbf y^k) \\ \mathbf H_{\mathbf u,\mathbf y}^k &{} \mathbf H_{\mathbf u,\mathbf u}^k &{} -D_\mathbf u\mathbf F^T(\mathbf u^k) \\ D_\mathbf y\mathbf B(\mathbf y^k) &{} -D_\mathbf u\mathbf F(\mathbf u^k) &{} 0 \end{pmatrix}&\begin{pmatrix} \mathbf y^{k+1}-\mathbf y^k \\ \mathbf u^{k+1}-\mathbf u^k \\ \mathbf p^{k+1}-\mathbf p^k \end{pmatrix} \nonumber \\&= - \begin{pmatrix} D_\mathbf yJ(\mathbf y^k,\mathbf u^k) + D_\mathbf y\mathbf B^T(\mathbf y^k) \mathbf p^k \\ D_\mathbf uJ(\mathbf y^k,\mathbf u^k) - D_\mathbf u\mathbf F^T(\mathbf u^k) \mathbf p^k \\ \mathbf B(\mathbf y^k) - \mathbf F(\mathbf u^k) \end{pmatrix} \end{aligned}$$
(36)

with

$$ \begin{pmatrix} \mathbf H_{\mathbf y,\mathbf y}^k &{} \mathbf H_{\mathbf y,\mathbf u}^k \\ \mathbf H_{\mathbf u,\mathbf y}^k &{} \mathbf H_{\mathbf u,\mathbf u}^k \end{pmatrix} = \begin{pmatrix} D_{\mathbf y,\mathbf y} L(\mathbf y^k,\mathbf u^k,\mathbf p^k) &{} D_{\mathbf y,\mathbf u} L(\mathbf y^k,\mathbf u^k,\mathbf p^k)\\ D_{\mathbf u,\mathbf y} L(\mathbf y^k,\mathbf u^k,\mathbf p^k) &{} D_{\mathbf u,\mathbf u} L(\mathbf y^k,\mathbf u^k,\mathbf p^k) \\ \end{pmatrix}. $$

If the linear systems in (36) become too large, we are pursuing the null space approach to arrive at the SQP formulation with the reduced Hessian for the increment \(\varDelta \mathbf u^k := \mathbf u^{k+1}-\mathbf u^k\):

$$\begin{aligned} \mathbf M( \mathbf y^k, \mathbf u^k) \varDelta \mathbf u^k = - \mathbf h( \mathbf y^k, \mathbf u^k), \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{aligned} \mathbf M( \mathbf y^k, \mathbf u^k) :=&\begin{pmatrix} D_\mathbf u\mathbf F^T (\mathbf u^k) D_\mathbf y\mathbf B^{-T}(\mathbf y^k)&Id \end{pmatrix} \begin{pmatrix} \mathbf H_{\mathbf y,\mathbf y}^k &{} \mathbf H_{\mathbf y,\mathbf u}^k \\ \mathbf H_{\mathbf u,\mathbf y}^k &{} \mathbf H_{\mathbf u,\mathbf u}^k \end{pmatrix} \begin{pmatrix} D_\mathbf y\mathbf B^{-1} (\mathbf y^k) D_\mathbf u\mathbf F(\mathbf u^k) \\ Id \end{pmatrix} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mathbf h( \mathbf y^k, \mathbf u^k) : =&D_\mathbf uJ(\mathbf y^k,\mathbf u^k) + D_{ \mathbf u} \mathbf F^T( \mathbf u^k) \lambda ^k \\&- \left( D_{ \mathbf u} \mathbf F^T( \mathbf u^k) D_{ \mathbf y} \mathbf B^{-T}( \mathbf y^k) \mathbf H_{\mathbf y,\mathbf y}^k + \mathbf H_{\mathbf u,\mathbf y}^k\right) D_{ \mathbf y} \mathbf B^{-1}( \mathbf y^k) \mathbf r( \mathbf y^k, \mathbf u^k)) \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \lambda ^k :=&D_{ \mathbf y} \mathbf B^{-T}(\mathbf y^k) D_\mathbf yJ(\mathbf y^k,\mathbf u^k) \,,&&\mathbf r( \mathbf y^k, \mathbf u^k) :=&\mathbf B( \mathbf y^k) - \mathbf F( \mathbf u^k). \end{aligned} \end{aligned}$$

We are using iterative methods, e.g. the conjugate gradient methods, to solve (37). Since in our case the number of control variables will be small we can expect convergence within very few iterations. Within each iteration step of the iterative method, we still have to solve the two linear systems corresponding to \(D_\mathbf y\mathbf B(\mathbf y^k)\) and \(D_\mathbf y\mathbf B^T(\mathbf y^k)\). Alternatively, if we have sufficient memory to store \(\mathbf M(\cdot ,\cdot )\), we can compute \(\mathbf M(\cdot ,\cdot )\) explicitly. Clearly, we never compute neither \(D_\mathbf y\mathbf B^{-1}(\mathbf y^k)\) nor \(D_\mathbf y\mathbf B^{-T}(\mathbf y^k)\) explicitly.

Once we know \(\varDelta \mathbf u^k\) we can compute \( \mathbf y^{k+1}\) and \( \mathbf p^{k+1}\) by:

$$\begin{aligned} \begin{aligned} \mathbf y^{k+1}-\mathbf y^{k}&= D_{ \mathbf y} \mathbf B^{-1}( \mathbf y^k) D_{ \mathbf u} \mathbf F( \mathbf u^k) \varDelta \mathbf u^k - \mathbf r( \mathbf u^k, \mathbf y^k), \\ \mathbf p^{k+1} + \lambda ^k&= - D_{ \mathbf y} \mathbf B^{-T}( \mathbf y^k) (\mathbf H_{\mathbf y,\mathbf y}^k (\mathbf y^{k+1}-\mathbf y^{k})+ \mathbf H_{\mathbf y,\mathbf u}^k (\mathbf u^{k+1}-\mathbf u^{k})). \end{aligned} \end{aligned}$$

We would like to highlight that the SQP-method relies on proper derivatives of the non-linear operators \(\mathbf B\) and \(\mathbf F\). In our case \(\mathbf F\) is affine, hence the derivative of \(\mathbf B\) remains the most difficult part. On the other hand these are exactly the same terms that appear in the Newton iterations for the direct problem (20) and we can reuse the methodology presented at the end of Sect. 4. For practical purposes we do neglect all involved second order derivatives of \(\mathbf B\).

It is very instrumental to compare the expression involved in the reduced formulation (37) of SQP to the gradient and the Hessian of the reduced cost function, that would appear when using algorithms for unconstrained optimization problems.

Fig. 5.
figure 5

The optimal voltages.

Full size image
Fig. 6.
figure 6

Optimal control for a ramp-up scenario: the plasma boundary (green) follows the prescribed boundary (black points), snapshots at \(t=0,2,6,10,20,30,40,45,50,54,58,60\,s\) (from left to right, top to down). (Color figure online)

Full size image

Let \(\widehat{J}(\mathbf u):= J(\mathbf y(\mathbf u),\mathbf u)\), with \(\mathbf B(\mathbf y(\mathbf u)) = \mathbf F(\mathbf u)\) be the reduced cost function, then we have the following expressions for gradient

$$\begin{aligned} D_\mathbf u\widehat{J}(\mathbf u) = D_\mathbf uJ(\mathbf y,\mathbf u) + D_{ \mathbf u} \mathbf F^T( \mathbf u), \lambda \end{aligned}$$

and Hessian

$$\begin{aligned} \begin{aligned} D_{\mathbf u,\mathbf u} \widehat{J}(\mathbf u) =&\mathbf Z^T \begin{pmatrix} D_{\mathbf y,\mathbf y} J(\mathbf y,\mathbf u) &{} D_{\mathbf y,\mathbf u} J(\mathbf y,\mathbf u) \\ D_{\mathbf u,\mathbf y} J(\mathbf y,\mathbf u) &{} D_{\mathbf u,\mathbf u} J(\mathbf y,\mathbf u) \\ \end{pmatrix} \mathbf Z\\&+ \mathbf Z^T \begin{pmatrix} - D_\mathbf y(D_\mathbf y\mathbf B^T(\mathbf y) \lambda ) &{}0 \\ 0&{} D_{\mathbf u} (D_\mathbf u\mathbf F^T(\mathbf u) \lambda ) \\ \end{pmatrix} \mathbf Z\end{aligned} \end{aligned}$$

with

$$\begin{aligned} \lambda = D_{ \mathbf y} \mathbf B^{-T}(\mathbf y) D_\mathbf yJ(\mathbf y,\mathbf u) \quad \text {and} \quad \mathbf Z= \begin{pmatrix} D_\mathbf y\mathbf B^{-1}(\mathbf y) D_\mathbf u\mathbf F(\mathbf u) \\ Id \end{pmatrix} \end{aligned}$$

Hence, the reduced gradient \(\mathbf h( \mathbf y^k, \mathbf u^k)\) is not the gradient of the reduced cost function, unless the state and control variable \(\mathbf y^k\) and \( \mathbf u^k\) verify the equation of state \(\mathbf B( \mathbf y^k) = \mathbf F( \mathbf u^k)\).

Preliminary Example. Finally, we would like to show first results for a so-called ramp-up scenario in an ITER-like tokamak, where the plasma evolves from a small circular to a large elongated plasma. The optimal coil voltages are depicted in Fig. 5. Then, if we use those as data to solve the direct problem we verify that the plasma boundary follows indeed the prescribed trajectory (see Fig. 6).

Conclusion. The study and the optimization of scenarios is more and more important for the realization of objectives in magnetic confinement controlled fusion and will certainly be crucial for the ITER project. The first results presented in this paper are very encouraging and are the starting point of the development of new tools devoted to the preparation of scenarios of the future devices.