Keywords

1 Introduction

The correct understanding of brain activity has been attracting significant relevance in the development of systems of assistance in the neuroscience field. In the last decade several works have been developed in order to improve the mapping and accurate detection of neural activity inside the brain in different scenarios [1, 4, 8]. The brain activity has been modeled by currents, more precisely by current dipoles that fit the neuronal potentials being generated within the brain cortex. Electroencephalography (EEG) has proved to be an effective method for capturing the electric brain activity. The EEG data has the property of a high temporal resolution but low spatial resolution [1, 4, 8].

Since there are few orders of difference between the number of possible brain sources with the number of electrodes, the problem of source reconstruction becomes ill-posed [1]. Due the ill-posed nature of the problem, some spatial and temporal priors should be included in order to find a unique solution. Methods that are used to solve the inverse problem are categorized in two approaches [6]. The first approach known as parametric methods, assume few dipoles inside the brain with unknown position and orientation, then, a non-linear problem is solved in order to estimate these parameters. The second approach of non-parametric methods, assume several dipoles within the brain volume, with fixed positions and orientations. A linear problem is solved in order to find the amplitudes and orientations of these assumed sources from the EEG data [4]. There is still a wide open field in which the EEG data could be effectively used for brain source reconstruction. Since the Minimum norm Estimate (MNE) and Low Resolution Tomography (LORETA) were proposed, some variations to these methods have been used for addressing this problem [5, 10]. From the non-parametric methods, a Bayesian framework could be used to deduce most of the methods based on regularization approaches of the inverse problem. In [8], a technical note for solving the source reconstruction problem from M/EEG data within a Bayesian framework is presented [8].

The objective when source reconstruction from EEG data is addressed is to reduce the localization error. The original LORETA and MNE approaches show a considerable high error localization of the sources [1]. Some variations of LORETA have tried to address the low resolution with some spatial and temporal transforms of the data and the prior covariance definition. Standardized LORETA (sLORETA) and standardized weighted LORETA (swLORETA) methods give lower error localization of the sources. Standardized LORETA (sLORETA) [11] proposes the use of a initialization of the current density estimate, given by MMN solution and then standardized values of the current density are inferred [11]. The sLORETA algorithm proves to reduce the localization dipole error results compared to LORETA. The swLORETA proposed in [9], uses a Single Value Decomposition (SVD) of the leadfield matrix in order to improve the spatial resolution. Some unsolved issues of this approach are related to the capability of the SVD linear relationships to modeling the noise adequately.

In this work, we propose the use of kernel functions in order to enhance and model the temporal relationships in the EEG data. This enhancement could derive in a considerable improvement in the source reconstruction results within the LORETA framework. A Gaussian kernel is applied over the EEG data, projecting it to another dimension in which a selection of the most relevant temporal modes within the data could be performed. This reduced data then is the input for the sLORETA and swLORETA methods to obtain the results of the source reconstruction. Different metrics of source localization are computed to compare the proposed method against the classic LORETA framework. The Dipole localization error (DLE), the euclidean distance (ED) and the dipole dispersion (DD) shows a considerable improvement of the proposed method in the source reconstruction problem.

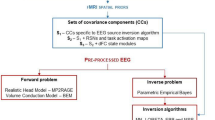
2 Materials and Methods

Description of the data used to develop this work is included in this section. A theoretical background of LORETA as the non-parametric method selected for source reconstruction is also presented. Finally the description of the metrics employed and the experimental setup are depicted. The Statistical Parametric Mapping (SPM) [3] is used in the 12.1 version, and is combined into Matlab 2014a. The data for source reconstruction analysis corresponds to generated synthetic EEG data. The SPM implementation for LORETA is used in order to compare and validate the results obtained from the proposed methodology.

2.1 Inverse Problem

The source reconstruction problem from M/EEG data could be formulated as follows:

$$\begin{aligned} \varPhi = \mathbf {KJ}, \end{aligned}$$
(1)

where \(\varPhi \in \mathbb {R}^{N\times s}\) is the set of observations from the N electrodes in s time samples, \(\hat{J} \in \mathbb {R}^{N\times M}\) is known as the current density in M possible sources inside the brain and \(K \in \mathbb {R}^{N\times M}\) is a gain matrix known as the Leadfield matrix [10]. For solving the inverse problem, the forward problem should be solved first in order to establish the relationships between the neural activity and how it maps into the set of M/EEG sensors [7].

2.2 LORETA

The solution of the inverse problem proposed in [10] sacrifices spatial resolution by assuming smoothness in the solution space. The functional that has to be minimized is presented in Eq. (2);

$$\begin{aligned} \mathop {\min }\limits _j {\left\| {BW\hat{J}} \right\| ^2}, \end{aligned}$$
(2)

where W is the diagonal matrix with elements \(w_{ii} = \left\| {K_i} \right\| \) and \(B_{3M\times 3M}\) is the Laplacian operator that ensures smoothness in the solution [10]. The solution for the estimated current density is obtained following Eq. (3);

$$\begin{aligned} \hat{J}=T\varPhi , \end{aligned}$$
(3)

with \(T = (W B^T B W)^{-1} K^T (K(W B^T B W)^{-1}K^T)^{\dag }\) and \(\dag \) denotes the Moore-Penrose inverse operator. Furthermore, swLORETA proposes a variation of the sLORETA method which includes a initialization of the current density from the Minimum Norm solution (MN) \(\hat{J}_{MN}\) and the use of a regularization parameter \(\alpha \) in the functional to be minimized, see Eq. (4). The swLORETA algorithm incorporates a SVD over the leadfield matrix in order to compensate the variations of the sensor sensitivity to currents at different depths [2, 9]. The SVD over \(\mathbf {K}\) is performed on the three columns corresponding to each dipole source location l in the three primary axes as \(K_l=U_i \varSigma _i V^T_i\). From these singular values, the current source density covariance matrix is constructed as Eq. (5).

$$\begin{aligned} F = \left\| {\varPhi -KJ} \right\| ^2 + \alpha \left\| J\right\| ^2 \end{aligned}$$
(4)
$$\begin{aligned} \left[ S^{1/2}_{\hat{J}} \right] = S^{-1/2} \otimes I_{3\times 3}, \end{aligned}$$
(5)

with \(I_{3\times 3}\) is the identity matrix, \(\otimes \) is the Kronecker product and \(S \in \mathbb {R}^{M\times M}\) a diagonal matrix with \(S_l\) elements being the maximum sensitivity at voxel l [2]. Furthermore, works like [1, 8] have proposed the use of a pre-processing stage. This pre-processing is related to the computing of the discrete cosine transform (DCT) over the EEG data. The DCT allows a filtering in the frequency domain before computing the SVD over the data. This approach of the DCT computing is performed within the kTE approach.

2.3 Kernel Temporal Enhancement

In order to improve the swLORETA method, we propose the use of a Gaussian kernel function to perform a temporal mapping of the data obtained from the sensors \(\varPhi \) (and after the DCT is computed).

$$\begin{aligned} \hat{\varPhi } = exp \left( - \frac{\left\| {\varPhi ^T - \varPhi } \right\| ^2}{2 \sigma ^2}\right) , \end{aligned}$$
(6)

obtaining a transformed input space \(\hat{\varPhi }\). From this transformed input space the first \(N_r\) eigenvalues with higher magnitude are selected to form the new input space from the corresponding eigenvectors as \(\hat{V} \in \mathbb {R}^{s\times N_r}\). The kernel parameter \(\sigma \) works as a noise filter, depending on a selected value, the transformation to the new input space will consider more or less noise. The threshold for the selection of the number \(N_r\) of temporal modes is set as the \(95\%\) of the normalized magnitude of the sum of all the eigenvalues. Then using the mapped input space, the covariance matrix \(S \in \mathbb {R}^{s \times s}\) is computed as a tensorial product between the linear and a Gaussian kernel relationships in the projected space, with \(\mathbb {K}_{\hat{\varPhi }_{cc'}} = exp(- \left\| \hat{\varPhi }_c V - \hat{\varPhi }_c' V \right\| / 2 \sigma _{\hat{\varPhi }}^2)\).

$$\begin{aligned} \mathbf {S} =\hat{\varPhi }V(\hat{\varPhi }V)^T \otimes \mathbb {K}_{\varPhi }. \end{aligned}$$
(7)

2.4 Reconstruction Error Metrics

For the validation of the results, some metrics that measure the correct source reconstruction are implemented. The Dipole Localization Error (DLE) measures the difference between the position of the simulated dipole \(\hat{V_o}\) against the position of the estimated dipole \(\hat{V_e}\), see Eq. (8). Another metric that measures the error in the source reconstruction is the Euclidean distance (ED) between the simulated and estimated dipole locations, see Eq. (9). Finally, The percent relative error is computed for the variance of the potential in the 1% source points surrounding the simulated dipole location. This gives us a measure of the dipole dispersion (DD), see Eq. (10).

$$\begin{aligned} DLE = \Vert \hat{V}_o - \hat{V}_e \Vert \end{aligned}$$
(8)
$$\begin{aligned} E_p = \sqrt{\left( V_{o_x}-V_{r_x} \right) ^2 + \left( V_{o_y}-V_{r_y} \right) ^2 + \left( V_{o_z}-V_{r_z} \right) ^2} \end{aligned}$$
(9)
$$\begin{aligned} DD = \frac{\left| Var(E(\hat{V}_o)_{0.1}) - Var(E(\hat{V}_o)_{0.1}) \right| }{Var(E(\hat{V}_o)_{0.1})} *100\% \end{aligned}$$
(10)

2.5 Experimental Setup

A set of \(M = 8196\) dipoles correspond to the discretization of the head volume and the sources that are simulated could take any of this M possible locations. The input data correspond of synthetic EEG signals with \(N = 128\) electrodes and \(s = 250\) time samples. The EEG signals are simulated with random locations of the source at different depths across the head volume. An analysis of different values of the SNR in the EEG data is performed. Signals with levels of 3dB, 5dB, 7dB, 10dB and 20dB are generated. From the LORETA framework, four scenarios of the method and pre-processing stages are analyzed. First, an swLORETA with spatial-SVD of the leadfield, temporal-SVD and linear covariance matrix calculation of the current density, with tag LORLL. Second, swLORETA with spatial-SVD of the leadfield, temporal-SVD and the Gaussian kernel covariance computation of the current density with tag LORLG. Finally, third and four scenario corresponde to swLORETA+kTE with spatial-SVD of the leadfield and kTE enhancement (with the DCT included) with linear covariance of the current density for LORGL and Gaussian kernel covariance of the current density for LORGG. For the kTE the kernel parameter \(\sigma \) in Eq. (6) is selected as factors of 1 times the value of the median of the kernelized input space. Finally, 20 EEG signals are generated for each SNR scenario in order to asses the statistical significance of each method following the error metrics computation.

3 Results

Figure 1 shows the reconstruction of the brain source for one random dipole. As can be seen form the figure the different combinations of preprocessing shows similar graphically results, due to this quantification of the dipole localization error is needed. Table 1 presents the DLE related to the different experiments for the three proposed SNR levels.

Table 1. Quantified results of source reconstruction, Dipole Localization Error (DLE), norm l1 distance error (ED) and Percent relative error/dipole dispersion (DD)
Full size table

In Table 1, it can be seen that the methods involving kTE, show less DLE compared with the other strategies for different SNR, with 7.13 being the lowest mean value for 10dB SNR. Also, it can be seen how for the lower values of SNR the strategies of LORGL and LORGG obtained lower mean value of the DLE in comparison with the other two strategies. From the second metric of error from Eq. (9), it can be seen a similar behavior compared to the DLE. For the lower values of SNR the kTE method proves to achieve lower mean errors across the 10 repetitions of the experiment. The lower mean level is 12.35 obtained for the 10dB signals. The last metric computed in this analysis is the percent relative error between the variance of the 1% points (from the whole head model) surrounding the dipole location in the original data, see Eq. (10).

The results presented in Table 1 for the DD metric, show that in the analysis of this metric, the proposed method of kTE improves the accuracy in the detection of the brain source. It can be seen that for all the SNR levels, the kTE method proves to reduce considerably the error in the source dispersion in comparison to the methods without kTE. In this particular metric the lower result is presented for the SNR of 20dB with a mean percent relative error of 70.82%. Some of the results in Table 1 are presented as box diagrams in Fig. 1(d), (e) and (f). A graphical analysis of these figures allows to compare the behavior of the three metrics for different experiments. While the DLE and ED metrics shows an improved mean value for the kTE methods against the classical methods, the DD shows an important improvement in the cases were kTE was used.

Fig. 1.
figure 1

Source reconstruction from EEG data for a simulated dipole. (a) presents the original source, (b) presents the results for reconstruction using the methods without kTE and figure (d) shows the reconstruction when kTE is used as was proposed in the experimental setup, (d, e and f) are Box diagram for the DLE, ED and DD of some source reconstruction experiments

Full size image

4 Discussion and Conclusions

An analysis of the results presented in the Sect. 3, allows us to determine that an improvement on the source recognition within the LORETA framework could be performed. In this case, the results when the kTE+LORETA method was employed shows less error on the localization than the classical LORETA methods. As higher as the influence of noise is, the kTE proves to model and remove the noise interference of the signals in the process of source reconstruction. This shows that the kernel function maps adequately the original data within a space where there are less influence of noise. The three metrics proposed to compare the methods shows lower mean levels of DLE, ED and DD when the kTE is employed. Even there is no statistical difference in DLE and ED metrics, since the standard deviation of the results is higher in the kTE case, the DD metric shows high difference for all the SNR levels. The results presented by the DD metric show a considerable improvement of the low resolution exhibited by LORETA. The results presented in this work allow us to conclude that an improvement with a pre-processing stage for EEG source reconstruction is possible. The mapping of the data using a kernel function as the kTE propose, allows to filter the noise of the data and improves the source localization results. Some improvements could be studied for this method, as the process of selection of the kernel parameters and the temporal modes to be included from the kernelized input space.