Hot Tiles: A Heat Diffusion Based Descriptor for Automatic Tile Panel Assembly

Abstract

We revisit the problem of forming a coherent image by assembling independent pieces, also known as the jigsaw puzzle. Namely, we are interested in assembling tile panels, a relevant task for art historians, currently facing many disassembled panels. Existing jigsaw solving algorithms rely strongly on texture alignment to locally decide if two pieces belong together and build the complete jigsaw from local decisions. However, pieces in tile panels are handmade, independently painted, with poorly aligned patterns. In this scenario, existing algorithms suffer from severe degradation. We here introduce a new heat diffusion based affinity measure to mitigate the misalignment between two abutting pieces. We also introduce a global optimization approach to minimize the impact of wrong local decisions. We present experiments on Portuguese tile panels, where our affinity measure performs considerably better that state of the art and we can assemble large parts of a panel.

1 Introduction

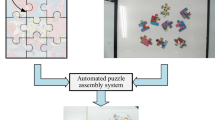
We are interested in providing automatic tools to address a problem of great relevance for art historians: the assembly of tile panels (Fig. 1).

Tile panel assembly is an instance of jigsaw puzzle assembly. In jigsaw, an image, often photographs of natural scenery, is split into several pieces. The objective is then to, without knowing the position nor orientation of each individual piece, recover the initial image.

Fig. 1.

Unsorted tiles at the Portuguese Tile’s Museum.

However, there are two main differences between tiles and jigsaw puzzles:

• 1. Tiles have poor texture: they often feature only two colors: white and blue.

• 2. Tiles have poor alignment between adjacent pieces: they are hand painted and individually baked

These two differences have a very strong impact on how we decide each piece position on the final panel. Namely, several algorithms [3, 7, 11] for jigsaw assembly rely strongly on texture alignment to locally decide if two pieces should be side by side and build the complete jigsaw from these local decisions. In this sense, the alignment between textures acts as an oracle that (almost) always guesses if any two pieces belong together in a given orientation or not. With the local responses from an oracle, knowing the jigsaw shape and the position of an initial piece we can solve the puzzle using a simple algorithm:

The most recent algorithm, introduced by Paikin et al. [11], uses a very similar approach, identifying abutting pairs of pieces with a confidence of $\sim$95 $\%$ using a dedicated affinity measure. These pairs are then used to ground the puzzle assembly. However, the affinity measure relies strongly on the existence of texture, and as we show in this paper, has only a $45\,\%$ accuracy when evaluated in tile panels. Thus, the problem of assembling tiles is considerably more difficult than the problem of assembling jigsaw puzzles from texture rich photographs.

In this work, we introduce a new affinity measure based on diffusion processes, that performs better than state of the art on our tile’s dataset. The affinity leverages on existing diffusion based descriptors [2] that represent not only a pixel, but also its neighborhood, and thus is more robust to misalignments, achieving a performance of 0.55 $\%$ in tile panels (Fig. 2).

Fig. 2.

Tile assembly: find the correct position and orientation of a set of pieces, or tiles, originally unsorted, so that they form a coherent image, or panel.

Notwithstanding the improvement we achieved, the affinity measure performance is still bellow the one obtained by the state of the art algorithms in jigsaw puzzles from photographs. Thus it cannot be used to replace the local oracle and we have to move to global affinity criteria to assemble tile panels. I.e., we propose to maximize the sum of the affinity over all abutting sides on the final panel reconstruction. To avoid the exhaustive search associated with such global function, we formulate the tile selection as a graph edge selection, which we then solve using a linear relaxation. To recover a solution in the binary space, we use Monte Carlo projection and show that, while we do not guarantee that we achieve global optimal, we can recover large parts of the complete panel, even with a modest number of trials.

Thus, the current paper innovates by introducing:

• a tile panel dataset¹

• a pairwise affinity measure that accounts for misalignments and poor texture;

• an algorithm for solving puzzles that uses a global affinity as criteria.

2 Dataset

In this work we introduce the seven 5$\,\times \,$5 tile panels represented in Fig. 3. All panels are painted in white and blue. All free parameters in the affinity measure were estimated using as subset of Panel 1 tiles.

3 Related Work

Our objective is to reconstruct a tile panel, without knowing a-priori information besides the panel final shape. Namely, we have no information on the tiles’ position nor orientation. This is an instance of a broader class of problems - the jigsaw puzzle assembly. Other instances have different constraints, e.g., there may be more a-priori information the pieces’ orientation may be known a-priori, or we may not have all the pieces in the puzzles. The type of puzzles influences how the puzzles are assembled, i.e., they influence the implementation of Algorithm 1 or other assembly approach. However, common to most approaches is the definition of the similarity between adjacent pieces, that acts as an oracle in those approaches but is very unreliable in tile panels. We here compare our affinity measure with previously propose ones, and discuss how the existing algorithms would fit the panel reconstruction problem.

Fig. 3.

Dataset of tile panels

3.1 Affinity Measure

As far as we are aware, all affinity measures between adjacent pieces compare color values, or similar functions, at a very shallow distance from the abutting boundary: no more that two rows/columns of pixels parallel to the boundary are used. Similar functions to the pixel color were based on the color gradient in the direction perpendicular to the abutting boundary.

Gallagher et al. [7] introduced a local affinity measure, linked to the difference in the gradient at the abutting edges of two adjacent pieces. Cho et al. [4] used directly the pixel color and Paikin et al. [11] compares not the color, but what the color should be based on the color gradient in the region perpendicular to the boundary.

The existing measures have showed very good results on current datasets created from photographs. In particular, Paikin showed very good results in finding best buddies (${>}95\,\%$), as we show in Table 1. Best buddies correspond to pairs of pieces that are simultaneously the most affine to one another, and thus should have higher accuracy, but lower recall, than just nearest neighbors. Several assembly algorithms, e.g., [11, 12], leverage on the identification of best buddies to assemble the whole puzzle.

The same table shows the results on the tile dataset, highlighting the need to define more relevant affinity measures to model the similarity between tiles. We note that, while we have obtained better results, we still have lower performances than those reported on photograph based datasets.

Table 1. Best buddies performance

3.2 Assembly

The first attempts to automatically solve jigsaw puzzles have been proposed by Freeman and Garder in 1964 [6]. In the last 15 years it has received renew attention, leading to an increase in the size of puzzles solved. However, most algorithms correspond to elaborated versions of Algorithm 1.

For example, Gallagher et al. [7] represents the puzzle as a graph, where edges connect abutting sides and carry a weight associated with the affinity of the two sides. Initially the algorithm considers edges connecting all possible combinations between all pieces, and then trims edges by finding a Minimum Spanning Tree (MST) [9], so that the final edges correspond to the abutting edges in the assembled jigsaw. The main difficulty with this approach is that the jigsaw shape has to be verified and corrected during iterations of MST. We also use a graph representation, but we introduce the jigsaw shape on the graph construction, namely on the definition of neighboring positions. Thus can use a global criteria.

Sholomon et al. [13] proposed an automatic jigsaw puzzle solver using genetic algorithm. In each iteration they generated hundreds of possible solutions, merging two “parent” to an improved “child” solution. It is performed by detecting, extracting and combining assembled puzzle segments.

Pomeranz et al. [12] and Paikin et al. [11] introduced approaches that rely heavily in finding pairs of pieces that had a very high probability of being together. They obtain such pairs by searching for best buddies. Furthermore, Paikin et al. [11] takes a step forward by solving puzzles where pieces are in unknown orientations or are altogether missing. In their approach, Paikin et al. avoid the complexity introduced by focusing on local decision and improving affinity measures. In our work, we also account for unknown orientations, but still aim at a global criteria for deciding on tiles positions.

There are several approaches [1, 4, 10] that look into the optimization of affinity between adjacent pieces using global criteria. However, all these approaches assume that the pieces orientation is known and thus do not extent naturally to unknown orientations.

Andaló et al. [1] presented a global formulation for jigsaw problems, Puzzle Solving by Quadratic Programming (PSQP). Cho et al. [4] presented a graphical model based on the patch transform to solve the jigsaw puzzle assuming some sort of previous knowledge. The authors propose an algorithm that minimizes a probability function via loopy belief propagation. Both formulations assume a one to one correspondence between pieces and positions in the puzzle. This assumption does not hold when we need to consider different orientations for each piece.

In our work, we model the solution as a global optimization problem, as in [1], but we extend the set of available pieces so that each tile in each orientation is counted as a different tile, while not being necessarily in the final panel. As in [4], we can also easily incorporate previous knowledge by changing the affinity of some tiles depending on their position in the panel.

Recent work has also been introduced using neural networks, [10], which solve small puzzles, by unsupervised learning images structures in a manner similar to [5]. This approach radically differs from previous ones as it does not depend on the similarity between points in two adjacent tiles. Instead it depends on the overall structure of shapes in our environment. However, it again cannot handle problems where the pieces orientation is unknown.

4 Heat Based Affinity Measure

To address the problem of poor texture or limited descriptive patterns, we introduce a new diffusion based affinity measure that can represent not only compatibility between pixels across the abutting boundary, but also of their neighborhood, providing some level of resilience to misalignment. Furthermore, we also aim at enhancing the pattern information by looking the alignment between regions of color transition in the boundary direction.

Diffusion based descriptors are often used to represent 3D shapes, but it was also showed that they can represent color and textures. In this work, we follow [2] and consider a diffusion process where color influences the rate of diffusion, leading to a color dependent, but misalignment resilient, affinity measure. We illustrate what we mean by color dependent diffusion with the three examples in Fig. 4 where we simulate the diffusion of a heat source over a tile. In the first example, corresponding to the first row, we consider only the tile shape. In the second example, second row, we consider a source at a lighter part of the tile and, at the third example, we consider a source at a darker part. The source is showed in red in the first column of Fig. 4 and in the subsequent columns (b $\sim$ f) we show the temperature increasing around the source following more or less a concentric shape. While this general effect is the same over the three examples, the temperature at each point changes between examples as the different colors propagate heat at different rates. It is of especial interest to our problem the fact that the rate at which the heat propagates in the neighborhood affects the temperature evolution at the source itself. Also, the relation between color and diffusion rate can be defined by a map that minimizes the affinity between incorrect pairings.

In the following we describe how to simulate heat diffusion over surfaces, which the familiar reader may jump. Then we show how we estimate the affinity used to compute the results presented in Table 1, including how we define the map between color and diffusion rate, and how we introduce the alignment at the color transitions into the overall affinity

4.1 Heat Diffusion on Color Surfaces

Heat diffusion is an umbrella term for the dynamic process that affects some quantity, we here refer to as temperature, described by a function $f(\bar{x},t): \mathbb R^n \times \mathbb R^+\rightarrow \mathbb R$ whose evolution in time is described by:

$$\begin{aligned} \nabla ^2 f(\bar{x}, t)= c(\bar{x})\partial _t f(\bar{x}, t), \end{aligned}$$

(1)

where $\bar{x}=[x_1,...,x_n]$ is a position vector, $\nabla ^2 f(\bar{x},t)$ is the Laplacian of function f and $c(\bar{x})$ is the heat conductivity at any given point.

The diffusion over tiles’ surface is a discrete version of the above equation. In this case $f(\bar{x},t)$ becomes a vector $\bar{f}(t) \in \mathbb R^N$ whose entry $[\bar{f}(t)]_i$ is the temperature at some pixel $v_i$ in the surface and the conductivity is represented by a vector $\bar{c}\in \mathbb R^N$ with a vector corresponding to the color at each pixel. In this work, we discretize the Laplacian operator using a distance based representation of L, where L is a weighted graph Laplacian where the weight of each edge is the inverse of its length:

$$\begin{aligned}&L \bar{f}(t) = \left( D-W\right) \bar{f}(t), \quad [W]_{v_i,v_j}=\left\{ \begin{array}{c c} 1/\Vert \bar{x}_{v_i}-\bar{x}_{v_j} \Vert ^2, &{} \quad \text {iff}\quad e_l=(v_j,v_i) \in E\\ 0, &{}\quad \text {otherwise} \end{array} \right. , \end{aligned}$$

(2)

and where D is a diagonal matrix with entries $D_{ii}=\sum _{j=1}^N [W]_{ij}$.

The equation allows to estimate a temperature at any time instant t given an initial temperature. In our work, and others previously [8], we consider a single source placed at some pixel s. In this case, the temperature can be written as

$$\begin{aligned} \bar{f}(t)= \sum _{i=1}^N \bar{\phi }_i^T \bar{f}(0) \exp (-\lambda _i t) [\bar{c}]_s \end{aligned}$$

(3)

Fig. 4.

Impact of color on diffusion. The first row corresponds to a diffusion process where all the points are equal. The second and third correspond to diffusion process where the rate depends on color. The red dot corresponds to the heat source on both cases. (Color figure online)

where $\lambda _i$ and $\bar{\phi }_i$ are the solution to the generalized eigenvalue problem $L\bar{\phi }_i = C \bar{\phi }_i \lambda _i$. Here C is a diagonal matrix whose entry $C_{l,l}$ is a scalar $c_l$ representing the color of pixel l. To move from RGB values to scalars, we use a map function $\gamma : \mathbb R^3 \rightarrow \mathbb R$, which we define shortly.

The temperature at each point will then depend both on the shape of the surface, in this case the rectangle formed by the two abutting tiles and in the color of both pieces. As the shape of the pieces is the same for all pairs, we remove this dependency. With that in mind, we first find the solution $\bar{f}_{\text {shape}}(t)$ corresponding to the upper row in Fig. 4, i.e., we solve Eq. 3 using the same L and the same initial condition but with $\bar{c}=\bar{1}$.

By dividing the solution with color $\bar{f} (t)$ by the solution at $\bar{f}_{\text {shape}} (t)$ we obtain a vector $\bar{g} (t):[\bar{g} (t)]_i=[\bar{f}(t)]_i/[\bar{f}_{\text {shape}}(t)]_i$ that depends on the color and on the neighborhood, but is not affected by shape.

4.2 Affinity Measure

As heat diffusion depends on the neighborhood of each point, it should be similar across points in two abutting sides. We access the affinity between two tiles by first placing the two side by side, as showed in Fig. 5(a), and then consider multiple sources $s_l$, at each side of the boundary, as showed in Fig. 5(b). For each source individually, we estimate $[\bar{g}(t')]_{s_l}$ at a fixed time instant $t'$. Finally, Fig. 5(c), shows how much $\bar{g}$ changes across the boundary in the two cases. In this last graphic, we note that positive values correspond to higher temperatures in the left tile, associated with darker colors in this region.

We note that the vector $\bar{g}^i$, containing all the temperature of all the ordered sources at tile i, changes smoothly for neighboring sources, even under large changes in the tile’s color. It is this smoothness that provides more resilient to misalignment than existing affinity measures. We thus compare the temperature for points in the same row/column, across boundaries: $\bar{\varDelta }^{1,2}: \bar{g}^{1}(t)-\bar{g}^{2}(t)$. The affinity corresponds to the sum of the squares of $\bar{\varDelta }$.

Fig. 5.

Computing affinity between two abutting tiles. The top images corresponds to a correct pair, while the second correspond to an incorrect pair.

We note that, as with other affinity measures for jigsaw puzzles, $\bar{\varDelta }^{1,2} \ne \bar{\varDelta }^{2,1}$, as when we switch tiles positions, the connecting sides are no longer the same. In the remaining of the paper, we always assume that $\varDelta ^{1,2}$ corresponds to the affinity between tile 1 and 2, when 1 is on the left side of 2 on a fixed orientation. By reasons that will be clear in Sect. 5, we consider all possible orientations of each physical tile as different tiles.

The overall process to compute the affinity measure between tiles $p_i$ and $p_j$, when $p_i$ is in the left side of $p_j$, is summarized in Algorithm 2.

4.3 Scalar Representation of Color

To use the above affinity definition, we need a map $\gamma : \mathbb R^3 \rightarrow \mathbb R$ between color and diffusion rate. We define such a map as the projection of each pixel color value $\mathcal I_{pixel}$ on an unit norm vector $\bar{\xi }\in \mathbb R^{+3}$. Such definition ensures that the map $\gamma$ (i) has a lower positive bound, i.e., that all generalized eigenvalues are positive and that $\bar{f} (t)$ converges, and that (ii) has an bound making the problem feasible.

Fig. 6.

Impact of different maps on the affinity measure.

We parameterize such vector as: $\bar{\xi }=[\cos (\theta ); \sin (\theta )\sin (\phi ); \sin (\theta )\cos (\phi )]$, for all $\theta ,\phi \in [0,\pi /2]$. Using several correct and incorrect pairs of puzzle 1 from the dataset, we searched for the parameters $\theta$ and $\phi$ that best minimized the distance between corrects and maximized the distance between incorrect.

Figure 6 shows that the distance function is convex on the chosen parameterization. Furthermore, it also shows that the minimum is close, but not equal, to the vector [0; 0; 1], which corresponds to a small deviation of the blue color. While we could have used convex optimization tools to further improve our estimation, we opted to use the minimum over this sparse sampling to avoid over-fitting to the small dataset of pairs we used to estimate the best distance.

4.4 Gradient Alignment

We want to align color transitions that occur in the boundary direction, so that Fig. 7(a) is less penalized than Fig. 7(b), as in the later there is match a between two distinctive patterns.

Fig. 7.

Gradient alignment.

Thus we introduce a second affinity measure that matches the gradient parallel to the boundary in both tiles, as illustrated in Fig. 7(c and d). For each pair of pieces, the affinity depends on the norm of the vector with the difference between the two gradients.

We combine the two affinities by means of a coefficient $\alpha$ so that $\mathcal A_{affinity}=\mathcal A_{heat} + \alpha \mathcal A_{align}$. Using panel 1 we found that $\alpha =0.11$ provided the best relation between precision and recall in best buddies.

5 Linear Programming for Tiling Reconstruction

As previously stated, we follow Gallagher [7] and represent the jigsaw problem as an edge selection problem in a graph. However, nodes in our graph representation correspond to all possible orientations of each tile at each position. Thus, for a panel with M tiles, the graph has $M^2\times 4$ nodes. Edges in the graph connect the nodes at abutting positions in the panel leading to $(M\times 4)^2$ for each pair of positions in the panel. The complete set of edges in a panel with $M_x \times M_y=M$ tiles positions is $\left[ (M_x-1)M_y +(M_y-1)M_x\right] \times 16 M^2$. Figure 8 shows and example of all possible nodes and edges for a puzzle $2 \times 2$. In Fig. 8(a) we represent all possible orientations of the four pieces. Each position in the panel will have associated a set of nodes corresponding to these orientations. The nodes in two abutting positions will be connected by edges, as showed in Fig. 8(b). The complete set of edges and nodes is represented in Fig. 8(c).

Each edge has an associated weight given by the affinity of the two sides of the tiles that it connects. Our objective is to select a single edge between abutting positions so that the global affinity is high. However, the set of edges must respect some global constraints that ensure that the puzzle is feasible, e.g., that all the edges connecting to a given position are associated with the same node.

The edge selection problem associated with these global constraints can be written as binary linear program, but is still an NP-Hard problem. While we can solve it for small problems, it does not escalate well with the size of the puzzle. As an example, a $4\times 4$ puzzle can take up to 2 h to solve. To allow scalability, we relax the problem to a linear program. To recover an integer solution from the relaxed problem, we introduce a Monte Carlo projection.

5.1 Binary Optimization Problem

To write the edge selection problem as an optimization problem, we represent any set of selected edges as vector $\bar{\tau }\in \{0,1\}^{16 \times M^2}$, such that $[\bar{\tau }]_i=1$ if we select edge i and $[\bar{\tau }]_i=0$ otherwise. Thus we want to optimize the function $y(\bar{\tau })=\bar{q}^T \bar{\tau }$, where $[\bar{q}]_{i}$ is the affinity between the two nodes connected by edge i.

Fig. 8.

Modeling a jigsaw puzzle structure as a graph.

We ensure a solution of the optimization problem corresponding to a feasible puzzle by introducing constraints in $\tau$. We can divide such constraints in four families:

The first is that between two abutting positions, we select one, and only one edge:

$$\begin{aligned} \bar{\tau }^T \mathbbm {1}^{\text {edge}}_{\mathcal E}=1, \quad \forall \mathcal E =1,...,(2M-M_x-M_y) \end{aligned}$$

(4)

where $\mathbbm {1}^{\text {tile}}_{\mathcal E}$ is an indicator vector, where $[\mathbbm {1}^{\text {tile}}_{\mathcal E}]_i=1$ if and only if the edge i is associated with the abutting tiles at position $\mathcal E$ in the panel and zero otherwise.

The second is that each tile should be chosen once, and can be expressed as:

$$\begin{aligned} \sum _{\mathcal P=1}^M\bar{\tau }^T \mathbbm {1}^{\text {tile}_{p,\mathcal P}}=w_{\mathcal P}, \quad \forall p=1,...,M \end{aligned}$$

(5)

where $[\mathbbm {1}^{\text {tile}}_{p,\mathcal P}]_i=1$ if and only if the edge i connects with tile p at the panel position $\mathcal P$, and $w_{\mathcal P}$ is the number of abutting positions to $\mathcal P$, e.g., for a corner the weight is 2.

The third is that edges connecting to a given position have to connect to the same node:

$$\begin{aligned} \bar{\tau }^T \left( w_{\mathcal P} \mathbbm {1}^{\varOmega }_{\omega ,\mathcal P}-[\mathbbm {1}^{\varOmega }_{\omega ,\mathcal P}]_t \right) = 0 \quad \forall \omega \in \varOmega \quad \mathcal P=1,...,M \quad t \in \mathcal E_{\omega , \mathcal P} \end{aligned}$$

(6)

where $[\mathbbm {1}^{\varOmega }_{\omega ,\mathcal P}]_i=1$ if and only if the edge i connects with a node $\omega \in \varOmega$, corresponding to some physical tile at a given orientation, at position $\mathcal P$ and zero otherwise. Furthermore, $\mathcal E_{\omega , \mathcal P}$ is the set of edges connecting to node $\omega$ in $\mathcal P$.

The forth removes symmetries resulting from the the puzzle structure, and is fundamental to avoid degenerate cases. The symmetries can be removed by considering that there is a tile with a single orientation. For example for $p=1$, instead of considering the whole set $\varOmega$, we must consider only a single orientation regardless of its position in the panel:

$$\begin{aligned} \bar{\tau }^T \mathbbm {1}^{\varOmega }_{\tilde{\omega }^{1},\mathcal P} = 0 \quad \forall \tilde{\omega }^{1}=1,...,3 M \quad \mathcal P=1,...,M \quad t \in \mathcal E_{\omega , \mathcal P} \end{aligned}$$

(7)

where $\tilde{\omega }^{1}$ corresponds to all possible orientations except 1.

Thus, we can formulate the jigsaw puzzle as the integer optimization problem:

$$\begin{aligned} \tau ^* = \arg \max _x\quad&\bar{q}^T \bar{\tau }\end{aligned}$$

(8)

$$\begin{aligned} \text {s.t.} A \bar{\tau }&=\bar{b} \quad [\bar{\tau }]_i\in \{0,1\} \end{aligned}$$

(9)

where A is a matrix with entries $[A]_{i,j}\in \mathbb N$ sparse matrix with $(2M-M_x-M_y) + M + 4M^2$ rows and $16 \times M^2\times (2M-M_x-M_y)$ columns. Each row of A corresponds to an indicator vectors $\mathbbm {1}$ from the above constraints. Finally $\bar{b}$ also has integer entries$[\bar{b}]_i\in N$.

Any prior information that we want to introduce in the solution, can be added directly by introducing more rows in A and $\bar{b}$.

5.2 Linear Relaxation

When we relax the above problem, we end up with a program whose solving time depends linearly on the total number of edges. The relaxed version of the above problem corresponds simply to replace Eq. 9 by $[\bar{\tau }]_i\in [0,1]$.

To recover an integer solution from the relaxed one, we use Monte Carlo projections. We first compute a relaxed version of the algorithm. Then, for each edge position $\mathcal E$, we associate the solution of the relaxed version to probability distributions on possible edges between tiles. We uniformly at random pick an edge position and, for that position, randomly select a connecting edge using the distribution. We then add the selected edge as a constraint to the linear optimization program and resolve it again. We iterate between sampling edges and solving the linear program until convergence, which often occurs after few iterations. After assigning an edge to each position, we have a binary solution, from which we can reconstruct a puzzle. However, we have no idea of how far we are from the minimum. We thus restart the projection several times, and look into the solutions with lower cost for the one that is able to better reconstruct tile panels.

Algorithm 3 summarizes the main steps of our algorithm for solving the relaxed version of our optimization formulation.

Fig. 9.

Best reconstructions, where polygons highlight correctly assembled parts

6 Results

Using the full binary solution, we were able to reconstruct a 4$\,\times \,$4 subpanel of Panel 1 from Fig. 3, provided that we used as an a-priori information that the first and second piece were connected at the top left corner.

For the full version of all the panels, without a-priori information and with the Monte Carlo projection, we cannot reconstruct the panels completely. However, we could recover large parts of each panel.

In Fig. 9 we present the best solutions, among the best 15 with highest affinity obtained from 100 independent Monte Carlo trials. And, to illustrate the difficulty of the dataset, we present in Table 2 the best buddies precision for each panel.

Table 2. Affinity precision on each panel

7 Conclusions

In this paper we introduced a variation to the known jigsaw problem, where the affinity between pieces is not reliable. We have introduced a new dataset of tile panels, which correspond to jigsaws with very little texture and severe misalignment. We introduced a novel affinity measure, which showed considerably better results than previous state of the art on this particular dataset. Finally, we have introduced a global approach for assembling jigsaw puzzles.

While the affinity precision is still too small and we cannot correctly assemble whole panels without a small external help, when looking at the final assembled panels it is clear that many pairings resulting from our algorithm are still visually convincing, at least locally. We note that this is particularly true in panels 4 and 5, which also have small affinity precisions. This highlights the difficulty of automatically reconstruct puzzles with little texture. On the other hand, the proposed approach can be used interactively by an art historian in the reconstruction of the complete panel.

We note that the results here presented were obtained using only 100 Monte Carlo trials for the projections, which took one day of computing using an Intel Core i7-5500u, with no parallelization and the Gurobi optimization package. As each trial is independent from all previous ones, in future work we expect to be able to further explore and improve on these results.