Parametric Model Discrimination for Heavily Censored Survival Data

Abstract

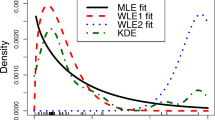
Abstract Simultaneous discrimination among various parametric lifetime models is an important step in the parametric analysis of survival data. We consider a plot of the skewness versus the coefficient of variation for the purpose of discriminating among parametric survival models. We extend the method of Cox and Oakes (1984, Analysis of Survival Data, Chapman & Hall/CRC)from complete to censored data by developing an algorithm based on a competing risks model and kernel function estimation. A by-product of this algorithm is a non-parametric survival function estimate.

Originally published in IEEE Transaction on Reliability, Volume 57, Number 2 in 2008, this paper makes extensive use of APPL from programming new ad hoc distributions to making new algorithms. Even the figures are produced by APPL. Of particular interest is the creation of the new procedure CalcNetHaz for calculating the net hazard function of the time to failure. Also APPL’s Mixture command allows one to generate kernals from many distributions, so that non-parametric analyses are possible with the Cox and Oakes charts. Also in the appendix is an excellent example of a simulation using APPL code embedded in other Maple procedures. Also of interest is the instantiation of particular Weibull distributions and so forth in Figure 14.10, made possible with APPL coding.

Appendices

Appendix 1

This appendix contains the APPL code to create the Cox and Oakes’ graph shown in Figure 14.1.

> unassign(’kappa’):

> lambda := 1:

> X := GammaRV(lambda, kappa):

> c := CoefOfVar(X):

> s := Skewness(X):

> GammaPlot := plot([c, s, kappa = 0.5 .. 999], labels = ["cv",

>              " skew"]):

> unassign(’kappa’):

> lambda := 1:

> X := WeibullRV(lambda, kappa):

> c := CoefOfVar(X):

> s := Skewness(X):

> WeibullPlot := plot([c, s, kappa = 0.7 .. 50.7]):

> unassign(’kappa’):

> lambda := 1:

> Y := LogNormalRV(lambda, kappa):

> c := CoefOfVar(Y):

> s := Skewness(Y):

> LogNormalPlot := plot([c, s, kappa = 0.01 .. 0.775]):

> unassign(’kappa’):

> lambda := 1:

> Y := LogLogisticRV(lambda, kappa):

> c := CoefOfVar(Y):

> s := Skewness(Y):

> LogLogisticPlot := plot([c, s, kappa = 4.3 .. 200.5]):

> cnsrgrp := plot([[0.5849304, 0.5531863]], style = point,

>                 symbol = box):

> cnsrgrp15 := plot([[0.6883908, 0.760566]], style = point,

>                 symbol = cross):

> cnsrgrp20 := plot([[0.7633863, 0.8009897]], style = point,

>                 symbol = diamond):

> with(plots):

> lll := textplot([0.17, 3.3, "log-logistic"], ’align =

>        {ABOVE, RIGHT}’):

> lnl := textplot([0.59, 3.3, "log-normal"], ’align =

>        {ABOVE, RIGHT}’):

> wbl := textplot([1.2, 3.3, "Weibull"], ’align =

>        {ABOVE, RIGHT}’):

> gml := textplot([1.3, 2.44, "gamma"], ’align =

>        {ABOVE, RIGHT}’):

> plots[display]({lll, lnl, wbl, gml, GammaPlot, WeibullPlot,

>        LogNormalPlot, LogLogisticPlot, cnsrgrp, cnsrgrp15,

>        cnsrgrp20}, scaling = unconstrained);

Appendix 2

Computational Issues. With our kernel density estimates being mixtures of large numbers of random variables, it became clear that even small data sets could result in piecewise functions with an unmanageable number of segments. To assist in the computation of these functions, we turned to APPL. In addition, APPL allows for the creation and combination of all types of standard random variables (uniform, normal, triangular, Weibull, etc.)—the very random variables we use in our kernel functions. The flexibility of APPL will allow for the efficient manipulation of many random variables.

Despite APPL’s comprehensive random variable handling ability, the equation at the core of our analysis, Eq. (14.1) has not been implemented. This necessitated our devising an algorithm (using the APPL language as a platform) that could perform the implementation of Eq. (14.1) for random variables defined in a piecewise manner. The Maple function CalcNetHaz calculates $h_{Y _{j}}(t)$ for crude lifetimes defined in a piecewise manner. It must be passed the APPL PDF for the numerator $f_{X_{j}}(t)$, a mixture of APPL survival functions for the denominator, and the numerator’s π _j values. The procedure CalcNetHaz returns the hazard function of the time to failure using Eq. (14.1). The code used to check for

• the correct number of arguments,

• the correct format for the PDF of the numerator and mixture of survivor functions in the denominator,

• the correct type (continuous) of random variables X ₁, X ₂, …, X _k ,

• the numerator given as a PDF and the denominator as a SF,

• 0 < π _j  < 1,

is suppressed for brevity. Since the kernel estimate for the failure and censoring distributions may be defined in a piecewise fashion (e.g., for a uniform or triangular kernel), the procedure accommodates piecewise distributions.

> CalcNetHaz := proc(num :: list(list), denom :: list(list),

>      NumPI :: float)

>   local retval, nsegn, i, j:

>   retval := []:

>   nsegn := nops(num[2]):

>   i := 1:

>   for j from 2 by 1 to nsegn do

>     while denom[2][i] < num[2][j] do

>       retval := [op(retval), unapply(simplify(

>                (NumPI * num[1][j - 1])

>                / denom[1][i])(x), x)]:

>       i := i + 1:

>     end do:

>   end do:

>   return([retval, denom[2], ["Continuous", "HF"]]):

> end:

The first two arguments to CalcNetHaz are lists of three lists, the last argument, π _j , is a scalar. The first list in the first parameter’s three lists is of the numerator’s n − 1 PDFs. These correspond to the n breakpoints in the numerator. The first list in the second parameter’s three lists is of the denominator’s m − 1 PDFs. These correspond to the m breakpoints in the denominator. These breakpoints are found in the second of the three lists. The third list contains the strings "Continuous" and either "PDF" or "SF" to denote the type of distribution representation. For each of the segments, the algorithm calculates a hazard function for the current segment based on Eq. (14.1). The algorithm assumes that the denominator is a mixture distribution involving the term in the numerator. This assumption can be made because in Eq. (14.1), since $S_{X_{j}}$ in the denominator is derived from $f_{X_{j}}$ in the numerator (or vice-versa) and results in denominator segment breaks that are a superset of those in the numerator. After looping through each of the segments, the algorithm returns the list of hazard functions along with the segment breaks of the denominator.

Appendix 3

This appendix contains the Monte Carlo simulation code in APPL necessary to conduct the experiments described in Section 14.5.

> n := 1000:

> kappa := 5:

> for i from 1 to 80 do

>   r := 0:

>   X1 := [ ]:

>   X2 := [ ]:

>   for k from 1 to n do

>     f := -log(UniformVariate()) ^ (1 / kappa):

>     c := -log(UniformVariate()) ^ (1 / kappa):

>     if f < c then

>       r := r + 1:

>       X2 := [op(X2), f]:

>     else

>       X1 := [op(X1), c]:

>     end if:

>   end do:

>   if r < n and r > 0 then

>     dists := [ ]:

>     weights := [ ]:

>     R := describe[quartile[3]](X1) - describe[quartile[1]](X1):

>     h := 0.79 * R * (n - r) ^ (-0.2):

>     for j from 1 to n - r do

>       weights := [op(weights), 1 / (n - r)]:

>       if h > sort(X1)[1] then

>         fd := fopen("mapsim2", APPEND):

>         fprintf(fd, "The following line was padded:

>                 h=%g min=%g\n", h, sort(X1)[1]):

>         fclose(fd):

>         h := sort(X1)[1]:

>       end if:

>       dists := [op(dists), UniformRV(X1[j] - h, X1[j] + h)]:

>     od:

>     f_X1 := Mixture(weights, dists):

>     dists := [ ]:

>     weights := [ ]:

>     R := describe[quartile[3]](X2) - describe[quartile[1]](X2):

>     h := 0.79 * R * (r ^ (-0.2)):

>     for j from 1 to r do

>       weights := [op(weights), 1 / r]:

>       if h > sort(X2)[1] then

>         fd := fopen("mapsim2", APPEND):

>         fprintf(fd, "The following line was padded: h=%g

>                 min=%g\n", h, sort(X2)[1]):

>         fclose(fd):

>         h := sort(X2)[1]:

>       end if:

>       dists := [op(dists), UniformRV(X2[j] - h, X2[j] + h)]:

>     od:

>     f_X2 := Mixture(weights, dists):

>     f_X12 := Mixture([(n - r) / n, r / n], [f_X1, f_X2]):

>     h_Y2 := CalcNetHaz(f_X2, SF(f_X12), evalf(r / n)):

>     f_Y2 := PDF(h_Y2):

>     mu := Mean(f_Y2):

>     ExpValueXSqrd := ExpectedValue(f_Y2, x -> x ^ 2):

>     sigma := sqrt(ExpValueXSqrd - mu ^ 2):

>     Term1 := ExpectedValue(f_Y2, x -> x ^ 3):

>     Term2 := 3 * mu * ExpValueXSqrd:

>     Term3 := 2 * mu ^ 3:

>     skew := (Term1 - Term2 + Term3) / sigma ^ 3:

>     cov := sigma / mu:

>     fd := fopen("mapsim2", APPEND):

>     fprintf(fd, "[[%g, %g]], \n", Re(cov), Re(skew)):

>     fclose(fd):

>   elif r = n then

>     skew := describe[skewness](X2):

>     cov := describe[coefficientofvariation](X2):

>     fd := fopen("mapsim4", APPEND):

>     fprintf(fd, "[[%g, %g]], \n", Re(cov), Re(skew)):

>     fclose(fd):

>   end if:

> end do: