Abstract
Branching bisimilarity and branching bisimilarity with explicit divergences are typically used in process algebras with silent steps when relating implementations to specifications. When an implementation fails to conform to its specification, i.e., when both are not related by branching bisimilarity [with explicit divergence], pinpointing the root causes can be challenging. In this paper, we provide characterisations of branching bisimilarity [with explicit divergence] as games between \(\textsc {Spoiler}\) and \(\textsc {Duplicator}\), offering an operational understanding of both relations. Moreover, we show how such games can be used to assist in diagnosing non-conformance between implementation and specification.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Abstraction is a powerful, fundamental concept in process theories. It facilitates reasoning about the conformance between implementations and specifications of a (software) system, described by a transition system. Essentially, it allows one to ignore (i.e., abstract from) implementation details that are unimportant from the viewpoint of the specification. While there is a wealth of behavioural equivalences (and preorders), each treating abstraction in slightly different manners, there are a few prototypical equivalences that have been incorporated in contemporary tool sets that implement verification technology for (dis)proving the correctness of software systems. These equivalences include branching bisimulation [19] and branching bisimulation with explicit divergence [18], which are both used in tool sets such as CADP [5], \(\mu \)CRL [2], and mCRL2 [4].
From a practical perspective, branching bisimulation and branching bisimulation with explicit divergence have pleasant properties. For instance, both relations are essentially compositional, permitting one to stepwise replace subcomponents in a specification with their implementations. Moreover, both types of branching bisimulation can be computed efficiently in \(\mathcal {O}(n\cdot m)\), where n is the number of states in a transition system and m is the number of transitions [8]. A recently published algorithm improves this to \(\mathcal {O}(m \log {n})\) [9].
The key idea behind both kinds of branching bisimulation is that they abstract from ‘internal’ events (events that are invisible to the outside observer of a system) while, at the same time, they remain sensitive to the branching structure of the transition system. This means that these relations preserve both the essential, externally visible, computations and the potential future computations of all states. At the same time, this can make it difficult to explain why a particular pair of states is not branching bisimilar, as one must somehow capture the loss of potential future computations in the presence of internal actions. While (theoretical) tools such as distinguishing formulae can help to understand why two states are distinguishable, these are not very accessible and, to date, the idea of integrating such formulae in tool sets seems not to have caught on.
We address the above concern by providing game-based views on branching bisimulation and branching bisimulation with explicit divergence. More specifically, we show that both branching bisimulation and branching bisimulation with explicit divergence can be characterised by Ehrenfeucht-Fraïssé games [17]. This provides an alternative point of view on the traditional coinductive definitions of branching bisimulation and branching bisimulation with explicit divergence. Moreover, we argue, using some examples, how such games can be used to give an operational explanation of the inequivalence of states following the ideas in [15], thereby remaining closer to the realm of transition systems.
Related Work. Providing explanations of the inequivalence of states for a given equivalence relation has a long tradition, going back to at least Hennessy and Milner’s seminal 1980 work [10] on the use of modal logics for characterising behavioural equivalences. Modal characterisations (and by extension, distinguishing formulae) for branching bisimulation appeared first in [11] and for branching bisimulation with explicit divergence in [18]. An alternative line of research has led to game-based characterisations of behavioural equivalences. For instance, in [16], Stirling provides a game-based definition of Milner and Park’s strong bisimulation [13]. More recently, Yin et al. describe a branching bisimulation game in the context of normed process algebra [20], but their game uses moves that consist of sequences of silent steps, rather than single steps. As argued convincingly by Namjoshi [12], local reasoning using single steps often leads to simpler arguments. A game-based characterisation of divergence-blind stuttering bisimulation (a relation for Kripke structures that in essence is the same as branching bisimulation), provided by Bulychev et al. in [3] comes closer to our work for branching bisimulation. However, their game-based definition is sound only for transition systems that are essentially free of divergences, so that in order to deal with transition systems containing divergences they need an additional step that precomputes and eliminates these divergences. Such a preprocessing step is a bit artificial, and makes it hard to present the user with proper diagnostics. As far as we are aware, ours is the first work that tightly integrates dealing with divergences in a game-based characterisation of a behavioural equivalence.
Structure of the Paper. Section 2 introduces the necessary preliminaries. In Sect. 3, we present our game-based definitions of branching bisimulation and branching bisimulation with explicit divergence and prove these coincide with their traditional, coinductive definitions. We illustrate their application in Sect. 4, while Sect. 5 shows how our results can be easily extended to the case of branching simulation. We conclude in Sect. 6.
2 Preliminaries
In this paper we are concerned with relations on labelled transition systems that include both observable transitions, and internal transitions labelled by the special action \(\tau \).
Definition 1
A Labelled Transition System (LTS) is a structure \(L = \langle S,A,\rightarrow \rangle \) where:
-
S is a set of states,
-
A is a set of actions containing a special action \(\tau \),
-
\({\rightarrow } \subseteq S \times A \times S\) is the transition relation.
As usual, we write \(s \xrightarrow {{a}} t\) to stand for \((s,a,t) \in \rightarrow \). The reflexive-transitive closure of the \(\xrightarrow {{\tau }}\) relation is denoted by \(\twoheadrightarrow \). Given a relation \(R \subseteq S \times S\) on states, we simply write \(s\mathrel {R} t\) to represent \((s,t) \in R\). We say that s is a divergent state if there is an infinite sequence \(s \xrightarrow {{\tau }} s_1 \xrightarrow {{\tau }} s_2 \cdots \).
Branching bisimulation was introduced by van Glabbeek and Weijland in [19].
Definition 2
([19]). A symmetric relation \(R \subseteq S \times S\) is said to be a branching bisimulation whenever for all \(s \mathrel {R} t\), if \(s \xrightarrow {{a}} s'\), then there exist states \(t', t''\) such that \(t \twoheadrightarrow t''\), with \(s\mathrel {R}t''\) and \(s'\mathrel {R}t'\); and either \(t'' \xrightarrow {{a}} t'\), or both \(a = \tau \) and \(t' = t''\). We write  and say that s and t are branching bisimilar, iff there is a branching bisimulation R such that \(s \mathrel {R} t\). Typically we simply write
and say that s and t are branching bisimilar, iff there is a branching bisimulation R such that \(s \mathrel {R} t\). Typically we simply write  to denote branching bisimilarity.
to denote branching bisimilarity.
Van Glabbeek et al. investigated branching bisimulations with explicit divergence in [18]. We here use one of their (many) equivalent characterisations:
Definition 3
([18, ConditionD2]). A symmetric relation \(R \subseteq S \times S\) is called a branching bisimulation with explicit divergence if and only if R is a branching bisimulation and for all \(s \mathrel {R} t\), if there is an infinite sequence \(s \xrightarrow {{\tau }} s_1 \xrightarrow {{\tau }} s_2 \cdots \), then there is a state \(t'\) such that \(t \xrightarrow {{\tau }} t'\) and for some k, \(s_k \mathrel {R} t'\). We write  iff there is a branching bisimulation with explicit divergence R such that \(s \mathrel {R} t\).
iff there is a branching bisimulation with explicit divergence R such that \(s \mathrel {R} t\).
Both kinds of branching bisimulations are equivalence relations.
Theorem 1
([1, 18]). Both  and
and  are equivalence relations. Moreover they are the largest branching bisimulation and branching bisimulation with explicit divergence, respectively.
are equivalence relations. Moreover they are the largest branching bisimulation and branching bisimulation with explicit divergence, respectively.
Both branching bisimulation relations and branching bisimulation with explicit divergence relations have the stuttering property [18, Corollary 4.4]. This will be useful in several of the proofs in this paper.
Definition 4
([18]). A relation R has the stuttering property if, whenever \(t_0 \xrightarrow {{\tau }} t_1 \cdots \xrightarrow {{\tau }} t_k\) with \(s \mathrel {R} t_0\) and \(s \mathrel {R} t_k\), then \(s \mathrel {R} t_i\), for all \(i \le k\).
3 Branching Bisimulation Games
The games we consider in this section are instances of two-player infinite-duration games with \(\omega \)-regular winning conditions, played on game arenas that can be represented by graphs. In these games each vertex is assigned to one of two players, here called \(\textsc {Spoiler}\) and \(\textsc {Duplicator}\). The players move a token over the vertices as follows. The player that ‘owns’ the vertex where the token is pushes it to an adjacent vertex, and this continues as long as possible, possibly forever. The winner of the play is decided from the resulting sequence of vertices visited by the token, depending on the predetermined winning criterion. We say that a player can win from a given vertex if she has a strategy such that any play with the token initially at that vertex will be won by her. The games that we consider here are memoryless and determined: every vertex is won by (exactly) one player, and the winning player has a positional winning strategy, so that she can decide her winning moves based only on the vertex where the token currently resides, without inspecting the previous moves of the play. These winning strategies can be efficiently computed while solving the game. We refer to [7] for a more in-depth treatment of the underlying theory.
3.1 The Branching Bisimulation Games
We start by presenting our game-based characterisation of branching bisimilarity. This will be extended to capture branching bisimulation with explicit divergence in Sect. 3.2.
Definition 5
A branching bisimulation (bb) game on an LTS L is played by players \(\textsc {Spoiler}\) and \(\textsc {Duplicator}\) on an arena of \(\textsc {Spoiler}\)-owned configurations \([\,(s,t),c,r\,]\) and \(\textsc {Duplicator}\)-owned configurations \(\langle \, (s,t),c,r\,\rangle \), where \(((s,t),c,r) \in \textit{Position}\times \textit{Challenge}\times \textit{Reward}\). Here \(\textit{Position}= S \times S\) is the set of positions, \(\textit{Challenge}= (A \times S) \cup \{ \dagger \}\) is the set of pending challenges, and \(\textit{Reward}= \{ *, \checkmark \}\) the set of rewards. By convention, we write \(((s,t),c,r)\) if we do not care about the owner of the configuration.
-
\(\textsc {Spoiler}\) moves from a configuration \([\,(s_0,s_1),c,r\,]\) by:
-
1.
selecting \(s_0 \xrightarrow {{a}} s_0'\) and moving to \(\langle \, (s_0,s_1),(a,s_0'),*\,\rangle \) if \(c = (a,s_0')\) or \(c = \dagger \), and to \(\langle \, (s_0,s_1),(a,s_0'),\checkmark \,\rangle \), otherwise; or
-
2.
picking some \(s_1 \xrightarrow {{a}} s_1'\) and moving to \(\langle \, (s_1,s_0),(a,s_1'),\checkmark \,\rangle \).
-
1.
-
\(\textsc {Duplicator}\) responds from a configuration \(\langle \, (s_0,s_1),c,r\,\rangle \) by:
-
1.
not moving if \(c=(\tau ,s_0')\) and propose configuration \([\,(s_0',s_1),\dagger ,\checkmark \,]\), or,
-
2.
if \(c = (a,s_0')\), moving \(s_1 \xrightarrow {{a}} s_1'\) if available and continue in configuration \([\,(s_0',s_1'), \dagger ,\checkmark \,]\), or
-
3.
if \(c \ne \dagger \), moving \(s_1 \xrightarrow {{\tau }} s_1'\) if possible and continue in configuration \([\,(s_0,s_1'), c,*\,]\).
-
1.
\(\textsc {Duplicator}\) wins a finite play starting in a configuration \(((s,t),c,r)\) if \(\textsc {Spoiler}\) gets stuck, and she wins an infinite play if the play yields infinitely many \(\checkmark \) rewards. All other plays are won by \(\textsc {Spoiler}\). We say that a configuration is won by a player when she has a strategy that wins all plays starting in it. Full plays of the game start in a configuration \([\,(s,t),\dagger ,*\,]\); we say that \(\textsc {Duplicator}\) wins the bb game for a position (s, t), if the configuration \([\,(s,t),\dagger ,*\,]\) is won by it; in this case, we write \(s \equiv _bt\). Otherwise, we say that \(\textsc {Spoiler}\) wins that game.
Note that by definition both players strictly alternate their moves along plays.
Remark 1
Our branching bisimulation game definition resembles the divergence-blind stuttering bisimulation (dbsb) game definition [3] of Bulychev et al. Apart from the different computational models, there are two fundamental differences: we maintain \(\textsc {Spoiler}\) ’s pending challenges and \(\textsc {Duplicator}\) ’s earned rewards, whereas the dbsb game does not, and our winning condition for \(\textsc {Duplicator}\) requires an infinite number of \(\checkmark \) rewards on infinite plays, whereas the dbsb game only requires \(\textsc {Duplicator}\) not to get stuck. However, both games are equivalent when played on LTSs in which there are no divergences. Instead, there are transition systems with divergent states that show that, unlike our bb game, the rules of [3] fail to capture branching bisimulation, see Example 1.
Let us explain how our game works intuitively: by keeping track of pending challenges and earned rewards, we can distinguish between \(\textsc {Duplicator}\) ‘facilitating’ progress (when choosing her first or second option) and \(\textsc {Duplicator}\) procrastinating (when choosing her third option) when facing challenges presented by \(\textsc {Spoiler}\). Procrastination is penalised by a \(*\) reward, but progress is rewarded by a \(\checkmark \) reward. On her account, \(\textsc {Spoiler}\) can either maintain a previously presented challenge, or change it if the challenge is still not totally solved by \(\textsc {Duplicator}\). In the latter case, \(\textsc {Spoiler}\) is penalised by rewarding \(\textsc {Duplicator}\) with a \(\checkmark \). This notion of pending challenge will be essential when extending the game so that it coincides with branching bisimulation with explicit divergence, as we will do in the next section. Omitting the concepts of pending challenges and earned rewards is what prevented extending the dbsb game to properly deal with divergent transition systems, and to (divergence sensitive) stuttering equivalence, in [3].
Before we prove that our bb game coincides with the classical co-inductive definition of branching bisimulation, we illustrate our game definition and a few of the subtleties we discussed above.
Example 1
Consider the LTS depicted in Fig. 1. Observe that \(s_0\) and \(t_0\) are branching bisimilar. Suppose \(\textsc {Spoiler}\) tries (in vain) to disprove that \(s_0\) and \(t_0\) are branching bisimilar and challenges \(\textsc {Duplicator}\) by playing \(s_0 \xrightarrow {{a}} c_1\). \(\textsc {Duplicator}\) may respond with an infinite sequence of \(\tau \)-steps, moving between \(t_0\) and \(t_1\), so long as \(\textsc {Spoiler}\) sticks to her challenge. In this way she would win the play following the rules in [3], but such procrastinating behaviour of \(\textsc {Duplicator}\) is not rewarded in our game. Instead, \(\textsc {Duplicator}\) has to eventually move to \(c_1\), matching the challenge, if she wants to win the play.
Now suppose \(\textsc {Spoiler}\) tries to disprove (again in vain) that \(s_0\) and \(t_0\) are branching bisimilar, and challenges \(\textsc {Duplicator}\) by playing \(t_0 \xrightarrow {{\tau }} t_1\). The only response for \(\textsc {Duplicator}\) is not to move at all, which completes the pending challenge, turning it into \(\dagger \), thus generating the new configuration \([\,(s_0,t_1), \dagger ,\checkmark \,]\). \(\textsc {Spoiler}\) may then challenge \(\textsc {Duplicator}\) by playing \(t_1 \xrightarrow {{\tau }} t_0\), and \(\textsc {Duplicator}\) can again respond by not moving. The infinite play that is produced is winning for \(\textsc {Duplicator}\), even if an infinite sequence of \(\tau \)-steps proving the divergence of \(t_0\) has been matched by \(\textsc {Duplicator}\) by staying totally idle, since \(\textsc {Duplicator}\) got infinitely many \(\checkmark \)s. Of course, things will be different when divergences will be taken into account in Sect. 3.2, since \(t_0\) is divergent, whereas \(s_0\) is not.
Before proving our first main theorem stating that two states are branching bisimilar just whenever \(\textsc {Duplicator}\) wins the associated game, we present two auxiliary results relating the winning configurations for this player.
Proposition 1
Configurations \([\,(s,t),c,*\,]\) and \([\,(s,t),c,\checkmark \,]\) are both won by the same player. Likewise, configurations \(\langle \, (s,t),c,*\,\rangle \) and \(\langle \, (s,t),c,\checkmark \,\rangle \) are both won by the same player.
Proof
This follows immediately from the Büchi winning condition: any player that wins some suffix of an infinite play also wins the infinite play itself. Furthermore, note that neither \(\textsc {Spoiler}\) nor \(\textsc {Duplicator}\) can get stuck playing a game by changing a reward from \(*\) to \(\checkmark \) or vice versa. \(\square \)
Definition 6
We say that a configuration \(((s,t),c,r)\) is consistent when either \(c=\dagger \), or \(c = (a,s')\) for some \(a,s'\) such that \(s \xrightarrow {{a}} s'\) in the given LTS.
Proposition 2
If \(\textsc {Duplicator}\) wins a consistent configuration \([\,(s,t),c,r\,]\), then \(\textsc {Duplicator}\) wins all consistent configurations \([\,(s,t),c',r'\,]\).
Proof
Let \([\,(s,t),c,r\,]\) be a \(\textsc {Spoiler}\)-owned consistent configuration that is won by \(\textsc {Duplicator}\). Towards a contradiction, assume \(\textsc {Spoiler}\) wins some consistent configuration \([\,(s,t),c',r'\,]\). Suppose \(\textsc {Spoiler}\) ’s winning strategy involves playing to configuration \(\langle \, (s,t),c'',r''\,\rangle \). Then from \([\,(s,t),c,r\,]\), \(\textsc {Spoiler}\) can force play to configuration \(\langle \, (s,t),c'',*\,\rangle \) or \(\langle \, (s,t),c'',\checkmark \,\rangle \): if \(c = \dagger \), then she can simply choose challenge \(c''\) while, if \(c = (a,s')\), she can change her challenge to \(c''\). But this leads to a contradiction: by Proposition 1, both configurations are won by \(\textsc {Spoiler}\), once \(\langle \, (s,t),c'',r''\,\rangle \) is won by \(\textsc {Spoiler}\). So \(\textsc {Duplicator}\) wins any \(\textsc {Spoiler}\)-owned consistent configuration \([\,(s,t),c',r'\,]\). \(\square \)
We next prove that the bb game captures branching bisimilarity. We split the proof obligations and prove both implications separately. First, we show that branching bisimilar states induce positions that are won by \(\textsc {Duplicator}\) in the bb game.
Lemma 1
If  then \(s \equiv _bt\).
then \(s \equiv _bt\).
Proof
We have to design a winning strategy for \(\textsc {Duplicator}\) for the game that starts in \([\,(s,t), \dagger ,*\,]\). We will call the consistent configurations \(((s',t'),c,r)\) corresponding to a position \((s',t')\), with  , good configurations (for player \(\textsc {Duplicator}\)). Let us first see that whenever \(\textsc {Spoiler}\) makes a move from a good configuration \([\,(s',t'),c',r'\,]\), then \(\textsc {Duplicator}\) can reply with a move to another good configuration. We distinguish cases according to the move selected by \(\textsc {Spoiler}\).
, good configurations (for player \(\textsc {Duplicator}\)). Let us first see that whenever \(\textsc {Spoiler}\) makes a move from a good configuration \([\,(s',t'),c',r'\,]\), then \(\textsc {Duplicator}\) can reply with a move to another good configuration. We distinguish cases according to the move selected by \(\textsc {Spoiler}\).
Assume \(\textsc {Spoiler}\) plays according to her first option and chooses a transition \(s' \xrightarrow {{a}} s''\). We distinguish cases depending on the nature of the executed action:
-
1.
if \(a = \tau \) and
 , then \(\textsc {Duplicator}\) can play choosing her first option getting the configuration \([\,(s'',t'),\dagger ,\checkmark \,]\), which clearly is good for her.
, then \(\textsc {Duplicator}\) can play choosing her first option getting the configuration \([\,(s'',t'),\dagger ,\checkmark \,]\), which clearly is good for her. -
2.
if \(a \not = \tau \) or
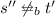 , then there exist states \(t_k',t''\) such that \(t' \twoheadrightarrow t_k'\),
, then there exist states \(t_k',t''\) such that \(t' \twoheadrightarrow t_k'\), 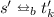 ,
, 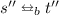 and \(t_k' \xrightarrow {{a}} t''\). Next we consider the length of the sequence of transitions that generates \(t' \twoheadrightarrow t_k'\). If this length is zero, then \(\textsc {Duplicator}\) can directly use her second option selecting the transition \(t' \xrightarrow {{a}} t''\) that generates \([\,(s'',t''), \dagger ,\checkmark \,]\), which is clearly good for her. If instead the sequence is not empty, then she can select the first transition \(t' \xrightarrow {{\tau }} t_1'\) of this sequence, and applying the stuttering property we have
and \(t_k' \xrightarrow {{a}} t''\). Next we consider the length of the sequence of transitions that generates \(t' \twoheadrightarrow t_k'\). If this length is zero, then \(\textsc {Duplicator}\) can directly use her second option selecting the transition \(t' \xrightarrow {{a}} t''\) that generates \([\,(s'',t''), \dagger ,\checkmark \,]\), which is clearly good for her. If instead the sequence is not empty, then she can select the first transition \(t' \xrightarrow {{\tau }} t_1'\) of this sequence, and applying the stuttering property we have  . Therefore, when \(\textsc {Duplicator}\) moves according to her third option, this produces configuration \([\,(s',t_1'), (a,s''),*\,]\), which is also good.
. Therefore, when \(\textsc {Duplicator}\) moves according to her third option, this produces configuration \([\,(s',t_1'), (a,s''),*\,]\), which is also good.
If \(\textsc {Spoiler}\) plays her second option, then the strategy \(\textsc {Duplicator}\) uses is the same that she would have used if \(\textsc {Spoiler}\) had played her first option from configuration \([\,(t',s'),c',r'\,]\).
When playing in this way, \(\textsc {Duplicator}\) will never get stuck, so that next it suffices to argue that she can select her moves as above in such a way that the generated play will contain an infinite number of \(\checkmark \) rewards. It is clear that the contrary could only happen if (1) \(\textsc {Spoiler}\) sticks to some fixed challenge \((a,s'')\) forever, as changing challenges is penalised with a \(\checkmark \); and (2) \(\textsc {Duplicator}\) replies generating a divergent sequence, i.e. choosing her third option, never earning a \(\checkmark \). But \(\textsc {Duplicator}\) can simply avoid generating such a sequence if the first time that the challenge is presented to her she selects any sequence \(t' \twoheadrightarrow t_k'\) as stated above, and then she plays by executing one by one the transitions in it, finally concluding by executing \(t_k' \xrightarrow {{a}} t''\), that will produce a new \(\checkmark \), thus generating the desired play with infinitely many \(\checkmark \) challenges. \(\square \)
Lemma 2
The relation \(\equiv _b\) is a branching bisimulation.
Proof
First, observe that \(\equiv _b\) is obviously symmetric, since starting from configuration \([\,(s,t),\dagger ,*\,]\), \(\textsc {Spoiler}\) can propose exactly the same challenges as when starting from \([\,(t,s),\dagger ,*\,]\), and the infinite suffixes of the resulting plays will therefore be identical, leading to the same winners.
Pick arbitrary s, t such that \(s \equiv _bt\) and assume \(s \xrightarrow {{a}} s'\). Let us see that \(\equiv _b\) meets the transfer condition. Since \(\textsc {Duplicator}\) has a winning strategy from \([\,(s,t),\dagger ,*\,]\), she has a winning move when \(\textsc {Spoiler}\) proposes the move \(s \xrightarrow {{a}} s'\) and configuration \(\langle \, (s,t),(a,s'),*\,\rangle \). We distinguish cases based on \(\textsc {Duplicator}\) ’s response in this winning strategy:
-
\(\textsc {Duplicator}\) replies according to her first option, by not making a move, producing the configuration \([\,(s', t), \dagger ,\checkmark \,]\). Then we have \(s' \equiv _bt\), and the transfer condition can be satisfied by choosing \(t'' = t' = t\).
-
\(\textsc {Duplicator}\) replies following her second option, thus selecting \(t \xrightarrow {{a}} t'\) to continue from the configuration \([\,(s', t'), \dagger ,\checkmark \,]\). This means that \(s' \equiv _bt'\), so that the transfer condition is satisfied by taking \(t'' = t\), since obviously \(s \equiv _bt''\) and \(s' \equiv _bt'\).
-
\(\textsc {Duplicator}\) replies following her third option, thus selecting \(t \xrightarrow {{\tau }} t_1'\) to continue from configuration \([\,(s, t_1'), (a, s'),*\,]\). This configuration is again won by \(\textsc {Duplicator}\), and then applying Proposition 2 we also have \(s \equiv _bt_1'\). Now, \(\textsc {Spoiler}\) could maintain the challenge \((a, s')\), and then the procedure can be repeated with \(\textsc {Duplicator}\) responding with her third move, until she can eventually play the second move, in order to get the reward that she eventually must be able to get, since she is playing a winning strategy. This final move by \(\textsc {Duplicator}\) will correspond to a transition \(t_k' \xrightarrow {{a}} t'\), and will produce the configuration \([\,(s', t'), \dagger ,\checkmark \,]\). Moreover, we had \(s \equiv _bt_k'\), so that taking \(t'' = t_k'\) the transfer condition is again satisfied.
So R is a branching bisimulation relation. \(\square \)
From the above lemmata, the following theorem follows immediately.
Theorem 2
We have  .
.
3.2 The Branching Bisimulation with Explicit Divergence Games
The results in the previous section demonstrate that maintaining pending challenges and earned rewards in the game play, and properly dealing with these in the winning condition, leads to an equivalence relation on states that coincides with branching bisimulation. It does not yet give rise to an equivalence that is sensitive to divergences. In fact, in Example 1 we already saw a pair of states \(s_0\) and \(t_0\) for which we have  , and therefore \(s_0 \equiv _bt_0\), while instead
, and therefore \(s_0 \equiv _bt_0\), while instead  .
.
As we argued in the previous section, by including challenges and rewards, our winning condition is able to reject plays in which \(\textsc {Duplicator}\) procrastinates forever. This addresses a part of the divergence problem: \(\textsc {Duplicator}\) cannot try to ‘prove’ two states equivalent modulo branching bisimulation simply by diverging when \(\textsc {Spoiler}\) does not ask for a divergence. However, \(\textsc {Duplicator}\) is still capable of matching a challenge of \(\textsc {Spoiler}\) that consists of a divergence by not diverging. Capturing explicit divergences can therefore only be achieved by clearly indicating when \(\textsc {Duplicator}\) replied to an internal move with another one, instead of just remaining idle. In the game definition we present below, we essentially do so by rewarding \(\textsc {Duplicator}\) in a new way only whenever she just properly responded with a matching move. Note that the changes required are subtle: assigning rewards differently would probably lead to different relations.
Definition 7
A branching bisimulation with explicit divergence (bbed) game on an LTS L is played by players \(\textsc {Spoiler}\) and \(\textsc {Duplicator}\) on an arena of \(\textsc {Spoiler}\)-owned configurations \([\,(s,t),c,r\,]\) and \(\textsc {Duplicator}\)-owned configurations \(\langle \, (s,t),c,r\,\rangle \), where \(((s,t),c,r) \in \textit{Position}\times \textit{Challenge}\times \textit{Reward}\). Here \(\textit{Position}= S \times S\) is the set of positions, \(\textit{Challenge}= (A \times S) \cup \{ \dagger \}\) is the set of pending challenges, and \(\textit{Reward}= \{ *, \checkmark \}\) the set of rewards. We again use the convention to write \(((s,t),c,r)\) if we do not care about the owner of the configuration.
-
\(\textsc {Spoiler}\) moves from a configuration \([\,(s_0,s_1),c,r\,]\) by:
-
1.
selecting \(s_0 \xrightarrow {{a}} s_0'\) and moving to \(\langle \, (s_0,s_1),(a,s_0'),*\,\rangle \) if \(c = (a,s_0')\) or \(c = \dagger \), and \(\langle \, (s_0,s_1),(a,s_0'),\checkmark \,\rangle \) otherwise; or
-
2.
picking some \(s_1 \xrightarrow {{a}} s_1'\) and moving to \(\langle \, (s_1,s_0),(a,s_1'),\checkmark \,\rangle \).
-
1.
-
\(\textsc {Duplicator}\) responds from a configuration \(\langle \, (s_0,s_1),c,r\,\rangle \) by:
-
1.
not moving if \(c=(\tau ,s_0')\) and propose configuration \([\,(s_0',s_1),\dagger ,*\,]\), or,
-
2.
if \(c = (a,s_0')\), moving \(s_1 \xrightarrow {{a}} s_1'\) if available and continue in configuration \([\,(s_0',s_1'), \dagger ,\checkmark \,]\), or
-
3.
if \(c \ne \dagger \), moving \(s_1 \xrightarrow {{\tau }} s_1'\) if possible and continue in configuration \([\,(s_0,s_1'), c,*\,]\).
-
1.
\(\textsc {Duplicator}\) wins a finite play starting in a configuration \(((s,t),c,r)\) if \(\textsc {Spoiler}\) gets stuck, and she wins an infinite play if the play yields infinitely many \(\checkmark \) rewards. All other plays are won by \(\textsc {Spoiler}\). We say that a configuration is won by a player when she has a strategy that wins all plays starting in it. Full plays of the game start in a configuration \([\,(s,t),\dagger ,*\,]\); we say that \(\textsc {Duplicator}\) wins the bbed game for a position (s, t), if the configuration \([\,(s,t),\dagger ,*\,]\) is won by it; in this case, we write \(s \equiv _b^{ed}t\). Otherwise, we say that \(\textsc {Spoiler}\) wins that game.
In order to understand how the new game works, note first that it is a (quite subtle!) refinement of the bb game. To be exact, only the first option in the description of \(\textsc {Duplicator}\) ’s moves is changed, simply turning the previously obtain reward \(\checkmark \) into \(*\), thus reducing the set of plays that are won by this player. As a consequence, any play \(\textsc {Duplicator}\) wins in the bbed game is also won by her in the bb game. Moreover, the original bb game can be recovered from the bbed game by weakening the winning condition of the latter as follows: an infinite play is won by \(\textsc {Duplicator}\) if the play yields infinitely many \(\checkmark \) rewards or \(\dagger \) challenges.
In contrast to the bb game, \(\textsc {Duplicator}\) now only earns a \(\checkmark \) reward when she fully satisfies a pending challenge (choosing her second option): she is now punished for choosing to not move (i.e. whenever she chooses her first option). As a result, whenever \(\textsc {Duplicator}\) is confronted with an infinite sequence of \(\tau \)-challenges produced by \(\textsc {Spoiler}\), effectively creating a divergent computation, \(\textsc {Duplicator}\) can no longer win such a play by choosing to stay put. Instead, \(\textsc {Duplicator}\) will need to collect a \(\checkmark \) mark from time to time, so that in the end she will be able to exhibit an infinite number of such marks.
Example 2
Reconsider the LTS in Fig. 1. In Example 1, we argued that \(\textsc {Spoiler}\) was not able to win the bb game starting in position \((s_0,t_0)\). Now reconsider \(\textsc {Spoiler}\) ’s strategy to challenge \(\textsc {Duplicator}\), by playing \(t_0 \xrightarrow {{\tau }} t_1\) in the bbed game. As before, \(\textsc {Duplicator}\) ’s only option is not to move. However, by not moving, \(\textsc {Duplicator}\) discharges \(\textsc {Spoiler}\) ’s (local) challenge, but she does not earn any \(\checkmark \) reward. Clearly, \(\textsc {Spoiler}\) can then challenge \(\textsc {Duplicator}\) by playing \(t_1 \xrightarrow {{\tau }} t_0\) in the bbed game, thereby forcing \(\textsc {Duplicator}\) to engage in an infinite play in which she earns no \(\checkmark \) reward, thus losing the game.
The above example suggests that, indeed, the reconsideration of challenges and rewards leads to a game in which \(\textsc {Spoiler}\) can explicitly check divergences. We next prove that the relation induced by the bbed game exactly captures branching bisimilarity with explicit divergence. We split the proof obligations into three separate lemmata.
Lemma 3
If  then \(s \equiv _b^{ed}t\).
then \(s \equiv _b^{ed}t\).
Proof
We again need to design the winning strategy for \(\textsc {Duplicator}\) for the bbed game that starts in \([\,(s,t), \dagger ,*\,]\). Since  implies
implies  , she could use the strategy defined in the proof of Lemma 1 to win the corresponding bb game. However, if we do not change anything in this strategy, it could be the case that \(\textsc {Spoiler}\) now wins the bbed game, since the strategy does not take divergences into account. Let us see which changes are needed to guarantee that \(\textsc {Duplicator}\) will also win the bbed game.
, she could use the strategy defined in the proof of Lemma 1 to win the corresponding bb game. However, if we do not change anything in this strategy, it could be the case that \(\textsc {Spoiler}\) now wins the bbed game, since the strategy does not take divergences into account. Let us see which changes are needed to guarantee that \(\textsc {Duplicator}\) will also win the bbed game.
First, note that all the positions along any play consistent with that winning strategy for \(\textsc {Duplicator}\) contain two  equivalent states, as we proved in Lemma 2. Second, observe that we start from a configuration \([\,(s,t), \dagger ,*\,]\) containing two
equivalent states, as we proved in Lemma 2. Second, observe that we start from a configuration \([\,(s,t), \dagger ,*\,]\) containing two  equivalent states, and in order to be able to repeat our arguments after any move of \(\textsc {Duplicator}\), we need to preserve that relation, and not just
equivalent states, and in order to be able to repeat our arguments after any move of \(\textsc {Duplicator}\), we need to preserve that relation, and not just  , as in the proof of Lemma 1.
, as in the proof of Lemma 1.
Concerning this new requirement, note that \(\textsc {Duplicator}\) ’s winning strategy designed to prove that lemma was based on  , but it is easy to see that now we can base it on
, but it is easy to see that now we can base it on  , so that the new winning strategy will preserve
, so that the new winning strategy will preserve  along the plays of that game that are consistent with that strategy.
along the plays of that game that are consistent with that strategy.
If we apply this strategy to the bbed game, the only case in which player \(\textsc {Duplicator}\) loses the game is that in which she is generating infinitely many \(\dagger \) challenges, but only finitely many \(\checkmark \) rewards. In particular, there would be some suffix of a play in which \(\textsc {Duplicator}\) generates infinitely many \(\dagger \) challenges, and earns no \(\checkmark \) reward. Next we consider that suffix as a full play and make a few observations about the moves played by both players along it:
-
\(\textsc {Spoiler}\) never plays her second move;
-
\(\textsc {Duplicator}\) never plays her second move;
-
\(\textsc {Duplicator}\) never plays her third move,
since in the first two cases, \(\textsc {Duplicator}\) would immediately earn a \(\checkmark \) reward, while in the third case, \(\textsc {Duplicator}\) will, by definition of the strategy used in the proof of Lemma 1, eventually earn a \(\checkmark \) reward after a finite sequence of \(\tau \)-moves.
Since \(\textsc {Duplicator}\) is always playing her first move, all challenges involved in the infinite suffix concern \(\tau \) actions; moreover, all rewards on this suffix are \(*\) rewards. Now observe that this infinite sequence of \(\tau \) successors of \(s_0\) consists of states that are all  -related to the state \(t_0\) \(\textsc {Duplicator}\) chooses to stay put in. But then, by definition of
-related to the state \(t_0\) \(\textsc {Duplicator}\) chooses to stay put in. But then, by definition of  , there must be some transition \(t_0 \xrightarrow {{\tau }} t'\) such that for some k,
, there must be some transition \(t_0 \xrightarrow {{\tau }} t'\) such that for some k,  , and then \(\textsc {Duplicator}\) can reply playing \(t_0 \xrightarrow {{\tau }} t_1\), instead of choosing her first option, thus collecting the needed \(\checkmark \) reward, and the play will continue from \([\,(s_k,t'), \dagger ,\checkmark \,]\).
, and then \(\textsc {Duplicator}\) can reply playing \(t_0 \xrightarrow {{\tau }} t_1\), instead of choosing her first option, thus collecting the needed \(\checkmark \) reward, and the play will continue from \([\,(s_k,t'), \dagger ,\checkmark \,]\).
Then, we will change the choice selected by \(\textsc {Duplicator}\) whenever the situation above appears, and in this way we get a revised strategy that will allow her to win the bbed game that starts in \([\,(s,t), \dagger ,*\,]\), thus proving \(s \equiv _b^{ed}t\). \(\square \)
Lemma 4
The relation \( \equiv _b^{ed}\) is a branching bisimulation.
Proof
As stated above, the bbed game is a refinement of the bb game: any configuration that is won in the bbed game is also won in the bb game. Hence, we can repeat the reasoning in the proof of Lemma 2 substituting the \(\checkmark \) reward by a \(*\) reward whenever \(\textsc {Duplicator}\) resorts to choosing her first option, to obtain the proof that \( \equiv _b^{ed}\) is a branching bisimulation. \(\square \)
The lemma below confirms that the relation induced by a bbed game is indeed sensitive to divergences.
Lemma 5
Let \(s \equiv _b^{ed}t\), and assume that we have a divergent sequence \(s = s_0 \xrightarrow {{\tau }} s_1 \xrightarrow {{\tau }} s_2 \xrightarrow {{\tau }} \cdots \). Then \(t \xrightarrow {{\tau }} t'\) for some \(t'\) such that for some k, \(s_k \equiv _b^{ed}t'\).
Proof
Let us suppose that for all \(t \xrightarrow {{\tau }} t'\), and for all k, we have \(s_k \not \equiv _b^{ed}t'\). Consider \(\textsc {Spoiler}\) ’s strategy that starts the game from \([\,(s_0,t),\dagger ,*\,]\) by making the move \(s_0 \xrightarrow {{\tau }} s_1\). Then \(\textsc {Duplicator}\) cannot reply moving to a \(\tau \)-successor of t, so that she has to play choosing her first option, which produces the configuration \([\,(s_i,t),\dagger ,*\,]\). Next \(\textsc {Spoiler}\) will play each of the moves \(s_i \xrightarrow {{\tau }} s_{i+1}\) in a row, and in all the cases \(\textsc {Duplicator}\) needs to stay idle, producing the configurations \([\,(s_i,t),\dagger ,*\,]\), that generate an infinite play without \(\checkmark \) rewards. Hence, \(\textsc {Spoiler}\) ’s strategy is winning for this bbed game, which contradicts the assumption that \(s \equiv _b^{ed}t\). \(\square \)
Theorem 3
We have  .
.
Proof
The inclusion  follows from Lemma 3. For the reverse, observe that \(\equiv _b^{ed}\) is a branching bisimulation with explicit divergence relation, since by Lemma 4 it is a branching bisimulation, that also fulfils the added obligation concerning divergences, as proved by Lemma 5. \(\square \)
follows from Lemma 3. For the reverse, observe that \(\equiv _b^{ed}\) is a branching bisimulation with explicit divergence relation, since by Lemma 4 it is a branching bisimulation, that also fulfils the added obligation concerning divergences, as proved by Lemma 5. \(\square \)
4 Some Small Applications
4.1 A Simple Application
The game-based definitions of branching bisimulation and branching bisimulation with explicit divergence provide an alternative, more dynamic view, on the standard coinductive definitions of these relations. A major benefit of any game-based characterisation of an equivalence relation is that it lends itself to explain, in a natural way, why two states in an LTS are not equivalent, when that is the case. Such an explanation is drawn directly from \(\textsc {Spoiler}\) ’s winning strategy in the branching bisimulation game. We illustrate this by showing how one can prove that an abstraction of a communication protocol over unreliable channels differs from a simple one-place buffer.
Example 3
Consider two LTSs below. The leftmost LTS models the abstraction of an implementation of a simple communication protocol for exchanging two types of messages (\(d_1\) and \(d_2\)), using a system of acknowledgements to cater for the unreliability introduced by a lossy/corrupting channel between sending and receiving parties. The LTS depicted below on the right models a simple specification of a one-place buffer for exchanging these two types of messages.

These LTSs are not branching bisimilar with explicit divergence. Since both are branching bisimilar, the difference between them must be in the lack of divergence in the specification. This is captured by \(\textsc {Spoiler}\) ’s winning strategy when playing the bbed game starting on \([\,(A,0),\dagger ,*\,]\), \(\textsc {Spoiler}\) can play against the designer of the implementation in a way similar to that in [15], allowing the designer to better understand the mistake. Such a play could proceed as is shown below:

Likewise, one can check that states B and 2 are not branching bisimilar with explicit divergence.
An alternative to illustrating the inequivalence between two states is through the use of a distinguishing formula. However, in many cases the nature of these formulae is rather ‘descriptive’ and requires a thorough understanding of modal logics, in order to understand its meaning. Instead, the game-based approach stays closer to the operational nature of LTSs. Moreover, the distinguishing formulae can become rather unwieldy, easily spanning several lines for states that are inequivalent for non-trivial reasons. The complexity of this approach is already illustrated by the following example, taken from [11].

Our game-based approach to distinguishing states 0 and A (in this case also under plain branching bisimulation equivalence) would start by \(\textsc {Spoiler}\) challenging by moving \(0 \xrightarrow {{a}} 1\), to which \(\textsc {Duplicator}\) can only respond by moving \(A \xrightarrow {{\tau }} B\). Now, continuing from \([\,(0, B), (a, 1),*\,]\) \(\textsc {Spoiler}\) plays her second option and challenges \(\textsc {Duplicator}\) to mimic move \(0 \xrightarrow {{b}} 4\), something that \(\textsc {Duplicator}\) cannot match.
The distinguishing formula given in [11] is \(\lnot ( (\textit{tt}\langle b \rangle \textit{tt}) \langle a \rangle \textit{tt})\), which holds at state A, but not at state 0. It explains that states 0 and A are inequivalent because state 0 may “engage in an a-step, while in all intermediate states (state 0 in this case) a b-step is available” [11], whereas this is not true of state A.
4.2 A More Elaborate Application
We illustrate how one can prove/argue interactively that the Alternating Bit Protocol with two messages differs (modulo branching bisimulation with explicit divergence) from a simple one-place buffer.
Example 4
Reconsider the one-place buffer for exchanging two different types of messages (\(d_1\) and \(d_2\)), as specified in Example 3. Suppose one tries to implement this one-place buffer using the Alternating Bit Protocol (see Fig. 2), only to find out that states A and 0 are not branching bisimilar with explicit divergences. In this case, \(\textsc {Spoiler}\) ’s winning strategy can be used to ‘play’ against the designer of the implementation in a way similar to that of [15], allowing the designer to better understand the reason why this implementation is not satisfactory. By solving the automatically generated game we obtain the following winning strategy for player \(\textsc {Spoiler}\), that proceeds as follows:

In a similar vein, one can check also that states B and 9 are not branching bisimilar with explicit divergence.
5 Branching Simulation Games
In this paper we have considered branching bisimulation [with explicit divergence]. Both relations are equivalence relations. When checking an implementation relation, sometimes it is desirable to drop this symmetry requirement, and use simulation relations, rather than bisimulation relations.
Whereas branching similarity has been studied before, see, e.g. [6], we are not aware of an exact simulation variant of branching bisimulation with explicit divergence, although the notion of divergence preserving branching simulation defined in [14] comes quite close.
A branching simulation game can be obtained from Definition 5 by disallowing \(\textsc {Spoiler}\) to choose her second option. The proof of the fact that the resulting preorder coincides with branching similarity proceeds along the same lines of that of Theorem 2. If we reconsider the example we took from [11] in Sect. 4.1, we note that state 0 is not branching simulated by state A, which can be proved following the same arguments as used in that section. Instead, state A is branching simulated by state 0, as the last can copy any move from the former, eventually arriving at states that are trivially equivalent.
A game characterisation of branching simulation equivalence can equally straightforwardly be obtained from our definitions, by only allowing \(\textsc {Spoiler}\) to choose her second option for her moves during the first round of the game, and disallowing this option in any subsequent rounds. Of course, the corresponding simulation equivalence relation that one obtains in this way is coarser than the corresponding bisimulation: \(\textsc {Spoiler}\) has a much bigger power if she can switch the board at any round. Similarly, from Definition 7 we could obtain games for branching simulation with explicit divergence and the corresponding simulation equivalence by restricting \(\textsc {Spoiler}\) ’s options.
6 Discussion & Future Work
In this paper we introduced game-theoretic definitions of branching bisimulation [with explicit divergence]. Compared to previous work, no transitive closure of \(\tau \)-transitions is needed in the game definition, so that we obtain a much more “local” assessment when two states are declared to be not equivalent. Additionally, divergence is dealt with as a first-class citizen: no precomputation of divergences, and subsequent modification of the game, is needed. The combination of these aspects leads to a game characterisation that enables diagnostics that apply directly to the original labelled transition systems.
Future Work. We have experimented with a prototype of the game-theoretic definitions of branching bisimulation (also with explicit divergence); we intend to make a proper implementation available in the mCRL2 tool set [4]. We leave further evaluating the effectiveness of the counterexamples described in this paper to future work. Furthermore, it can be investigated whether our approach of dealing with internal transitions extends to other behavioural equivalences, such as weak (bi)simulation.
References
Basten, T.: Branching bisimilarity is an equivalence indeed!. Inform. Process. Lett. 58(3), 141–147 (1996)
Blom, S., Fokkink, W.J., Groote, J.F., van Langevelde, I., Lisser, B., van de Pol, J.: mgrCRL: a toolset for analysing algebraic specifications. In: Berry, G., Comon, H., Finkel, A. (eds.) CAV 2001. LNCS, vol. 2102, pp. 250–254. Springer, Heidelberg (2001)
Bulychev, P.E., Konnov, I.V., Zakharov, V.A.: Computing (bi)simulation relations preserving CTL*-X for ordinary and fair Kripke structures. Inst. Syst. Program. Russ. Acad. Sci. Math. Meth. Algorithm 12, 59–76 (2007)
Cranen, S., Groote, J.F., Keiren, J.J.A., Stappers, F.P.M., de Vink, E.P., Wesselink, W., Willemse, T.A.C.: An overview of the mCRL2 toolset and its recent advances. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013 (ETAPS 2013). LNCS, vol. 7795, pp. 199–213. Springer, Heidelberg (2013)
Garavel, H., Lang, F., Mateescu, R., Serwe, W.: CADP 2011: a toolbox for the construction and analysis of distributed processes. Int. J. Softw. Tools Technol. Transf. 15(2), 89–107 (2013)
Gerth, R., Kuiper, R., Peled, D., Penczek, W.: A partial order approach to branching time logic model checking. Inform. Comput. 150(2), 132–152 (1999)
Grädel, E., Thomas, W., Wilke, T. (eds.): Automata Logics, and Infinite Games. LNCS, vol. 2500. Springer, Heidelberg (2002)
Groote, J.F., Vaandrager, F.W.: An efficient algorithm for branching and stuttering equivalence. In: Paterson, M.S. (ed.) Automata, Languages and Programming. LNCS, vol. 443, pp. 626–638. Springer, Heidelberg (1990)
Groote, J.F., Wijs, A.: An O(m log n) algorithm for stuttering equivalence and branching bisimulation. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 607–624. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49674-9_40
Hennessy, M., Milner, R.: On observing nondeterminism and concurrency. In: de Bakker, J., van Leeuwen, J. (eds.) Automata, Languages and Programming. LNCS, vol. 85, pp. 299–309. Springer, Heidelberg (1980)
Korver, H.: Computing distinguishing formulas for branching bisimulation. In: Larsen, K.G., Skou, A. (eds.) CAV 1991. LNCS, vol. 575, pp. 13–23. Springer, Heidelberg (1992)
Namjoshi, K.S.: A simple characterization of stuttering bisimulation. In: Ramesh, S., Sivakumar, G. (eds.) FST TCS 1997. LNCS, vol. 1346, pp. 284–296. Springer, Heidelberg (1997)
Park, D.: Concurrency and automata on infinite sequences. In: Deussen, P. (ed.) Theoretical Computer Science. LNCS, vol. 104, pp. 167–183. Springer, Heidelberg (1981)
Reniers, M.A., Schoren, R., Willemse, T.A.C.: Results on embeddings between state-based and event-based systems. Comput. J. 57(1), 73–92 (2014)
Stevens, P., Stirling, C.: Practical model-checking using games. In: Steffen, B. (ed.) TACAS 1998. LNCS, vol. 1384, pp. 85–101. Springer, Heidelberg (1998)
Stirling, C.: Modal and temporal logics for processes. In: Moller, F., Birtwistle, G. (eds.) Structure versus Automata. LNCS, vol. 1043, pp. 149–237. Springer, Heidelberg (1996)
Thomas, W.: On the Ehrenfeucht-Fraïssé game in theoretical computer science. In: Gaudel, M.-C., Jouannaud, J.-P. (eds.) TAPSOFT’93: Theory and Practice of Software Development. LNCS, vol. 668, pp. 559–568. Springer, Heidelberg (1993)
van Glabbeek, R.J., Luttik, S.P., Trçka, N.: Branching bisimilarity with explicit divergence. Fundam. Inform. 93(4), 371–392 (2009)
van Glabbeek, R.J., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. J. ACM 43(3), 555–600 (1996)
Yin, Q., Fu, Y., He, C., Huang, M., Tao, X.: Branching bisimilarity checking for PRS. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014, Part II. LNCS, vol. 8573, pp. 363–374. Springer, Heidelberg (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
de Frutos Escrig, D., Keiren, J.J.A., Willemse, T.A.C. (2016). Branching Bisimulation Games. In: Albert, E., Lanese, I. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2016. Lecture Notes in Computer Science(), vol 9688. Springer, Cham. https://doi.org/10.1007/978-3-319-39570-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-39570-8_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39569-2
Online ISBN: 978-3-319-39570-8
eBook Packages: Computer ScienceComputer Science (R0)






 , then
, then 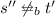 , then there exist states
, then there exist states 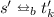 ,
, 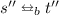 and
and  . Therefore, when
. Therefore, when 