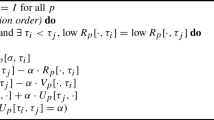Homology Computation During an Incremental Construction Process

Abstract

Controlling the construction of geometric objects is important for several Geometric Modeling applications. Homology (groups and generators) may be useful for this control. For such incremental construction processes, it is interesting to incrementally compute the homology, i.e. to deduce the homological information at step s of the construction from the homological information computed at step $s-1$. We here study the application of effective homology results [13] for such incremental computations.

1 Introduction

Geometric Modeling deals with the representation and the construction of geometric objects. For instance, many representations and related construction operations have been conceived for CAD/CAM applications; since a modeled geometric object can be manufactured, it is necessary to control its construction, in order to detect any problem as soon as possible. According to the application, homology (i.e. homology groups and/or the correspondence between their generators and chains of cells of the object at each step of its construction) may be useful for controlling the construction.

Many works in Geometric Modeling deal with subdivided geometric objects, i.e. objects partitioned into cells of different dimensions, and many methods have been proposed for computing the homology of subdivided objects, e.g. based upon the Smith Normal Form of incidence matrices [1]. Such methods make it possible to compute the homology at each step of the construction of a geometric object; but the whole homological information has to be computed at each step, without taking advantage of the information known at the previous step. So, it seems interesting for such a process to incrementally compute the homology, i.e. to deduce the homology of the object at step s from the homology of the object at step $s-1$, according to the operation which is applied. Such incremental computation can be done by applying results of effective homology [13].

Although some aspects are close to the work described in [6], the approach here focuses on the application of construction operations and the related complexities. Since only the structure of an object has to be taken into account in order to compute its homology, it will be assumed that it is represented by a semi-simplicial set or a cellular combinatorial structure (incidence graph or combinatorial map). In the simplicial (resp. cellular) case, two basic operations (and the inverse operations) are studied¹: cone and identification (resp. extension and identification), which make it possible to construct any semi-simplicial set (resp. any cellular combinatorial structure). At each step, some “homological information” is maintained in order to reduce the complexity of the homology computation. This “homological information” depends on the (subset of) combinatorial structure which is taken into account: for semi-simplicial sets and a subclass of cellular combinatorial structures, a “homological information” related to connected components is maintained; but it is necessary to maintain a “homological information” associated with cells and connected components for cellular combinatorial structures in general. More precision can be found in [3].

Notations. A chain complex $(C, \partial )$ can be associated with a semi-simplicial set or a cellular combinatorial structure S, in such a way that there is a strong correspondence between them (for instance, a generator of the chain complex is associated with any simplex, and the boundary operator is deduced from the face operators). Chain complex (H, 0) (or equivalently H) denotes the homology of S. The complexity of a chain complex, or a combinatorial structure, is related to the number of generators and the “cost” of the face or boundary operators (in terms of generators): for instance, the complexity of a n-dimensional semi-simplicial set (or its associated chain complex) is $\sum _{i=0}^n k_i c_i + \sum _{i=1}^n (i+1) k_i d_{i-1}$, where $k_i$ is the number of i-simplices, $c_i$ (resp. $d_i$) is the complexity of the representation of a i-simplex (resp. of a i-simplex in the boundary of a $(i+1)$-simplex).

2 Effective Homology Bases

This section is mainly based on the course notes of J. Rubio and F. Sergeraert [13] (see also [5]).

A reduction $\rho = ((C,\partial ),(C^S,\partial ^{\scriptscriptstyle S}), h, f, g)$ is a 5-tuple where (1) $(C,\partial )$ and $(C^S,\partial ^{\scriptscriptstyle S})$ are chain-complexes; (2) $f : (C,\partial ) \rightarrow (C^S,\partial ^{\scriptscriptstyle S})$ and $g: (C^S,\partial ^{\scriptscriptstyle S}) \rightarrow (C,\partial )$ are chain-complex morphisms; (3) $h: (C,\partial ) \rightarrow (C,\partial )$ is a graded module morphism of degree $+1$. They satisfy²: (4) $g f = id_{C^S}$; (5) $f g + h\partial +\partial h = id_{C}$; (6) $h f = g h = h h = 0$. Reduction $\rho$ will be sometimes symbolized by $(C,\partial )\mathop {\Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow }\limits ^{\rho } (C^S, \partial ^{\scriptscriptstyle S})$. The homologies of $(C,\partial )$ and $(C^S,\partial ^{\scriptscriptstyle S})$ are isomorphic, and the complexity of $(C^S,\partial ^{\scriptscriptstyle S})$ is lower than that of $(C,\partial )$; so, the homology of $(C,\partial )$ is computed with a better complexity starting from $(C^S,\partial ^{\scriptscriptstyle S})$. Several methods are based on (composition of) elementary reductions³ in order to simplify a chain complex before computing its homology [9, 11].

A homological equivalence $\Upsilon$ is a pair of reductions $(C,\partial ) \mathop {\Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow }\limits ^{\rho } (C^{B},\partial ^{\scriptscriptstyle B}) \mathop {\Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow }\limits ^{\rho ^{\scriptscriptstyle S}} (C^{S},\partial ^{\scriptscriptstyle S})$. This notion makes it possible to associate a “small” chain complex $(C^{S},\partial ^{\scriptscriptstyle S})$ with another chain complex $(C,\partial )$, through a “bigger” one $(C^{B},\partial ^{\scriptscriptstyle B})$, even when no reduction $(C,\partial ) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (C^S, \partial ^{\scriptscriptstyle S})$ exists.

An effective short exact sequence $((C^0,\partial ^{\scriptscriptstyle 0}), (C^1,\partial ^{\scriptscriptstyle 1}), (C^2,\partial ^{\scriptscriptstyle 2}), i, j, r, s)$ is a diagram:

where (1) $(C^0,\partial ^{\scriptscriptstyle 0})$, $(C^1,\partial ^{\scriptscriptstyle 1})$, $(C^2,\partial ^{\scriptscriptstyle 2})$ are chain complexes; (2) i,j are chain complex morphisms; (3) r,s are graded module morphisms. They satisfy (4) $ir = id_{C^0}$; (5) $ri+js=id_{C^1}$; (6) $sj=id_{C^2}$. This notion is a key one for optimizing the homology computation at each step of an incremental construction process; indeed, if an effective short exact sequence can be associated with the applied operation, the following SES theorem can be applied (only the subparts of the theorem which are useful here are provided: cf. [13] page 71).

Theorem 1

(SES Theorem). Let $((C^0,\partial ^{\scriptscriptstyle 0}), (C^1,\partial ^{\scriptscriptstyle 1}), (C^2,\partial ^{\scriptscriptstyle 2}), i, j, r, s)$ be a short exact sequence. Then, given two homological equivalences $\Upsilon ^0 : (C^0,\partial ^0) {\Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow }$ $(C^{B0},\partial ^{\scriptscriptstyle B0}) {\Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow } (C^{S0},\partial ^{\scriptscriptstyle S0})$ and $\Upsilon ^1 : (C^1,\partial ^1) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (C^{B1},\partial ^{\scriptscriptstyle B1}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (C^{S1},\partial ^{\scriptscriptstyle S1})$ (resp. $\Upsilon ^2 : (C^2,\partial ^{\scriptscriptstyle 2}) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (C^{B2},\partial ^{\scriptscriptstyle B2}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (C^{S2},\partial ^{\scriptscriptstyle S2})$), it is possible to deduce from i, j, r, s, $\Upsilon ^0$ and $\Upsilon ^1$ (resp. $\Upsilon ^2$) a homological equivalence $\Upsilon ^2 : (C^2,\partial ^{\scriptscriptstyle 2}) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (C^{B2},\partial ^{\scriptscriptstyle B2}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (C^{S2},\partial ^{\scriptscriptstyle S2})$ (resp. $\Upsilon ^1 : (C^1,\partial ^1) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (C^{B1},\partial ^{\scriptscriptstyle B1}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (C^{S1},\partial ^{\scriptscriptstyle S1})$).

If the applied operation “corresponds” to a short exact sequence, and if the operands of the operation are associated with homological equivalences, it is possible to deduce a homological equivalence, and thus a (homologically equivalent) “small” complex, for the result of the operation, providing a better complexity for the final homology computation⁴. Of course, it is also necessary to check the complexity of the application of the SES theorem in order to check that the whole computation is better than, say, a computation based upon the computation of the Smith Normal Form of the incidence matrices.

3 Application to Simplicial Structures

The SES theorem has been applied in order to reduce the cost of the homology computation [14]. For instance, Boltcheva et al. [5] applied it for the conception of the Mayer-Vietoris (MV) algorithm, which computes the homological information of abstract simplicial complexes from the homological information of sub-complexes and their intersections. This algorithm has been applied for the Manifold-Connected decomposition of abstract simplicial complexes [6]. The basic idea is the following: let B and C be sub-complexes of A, such that $A = B \cup C$, and $\Upsilon _{B \cap C}$, $\Upsilon _B$ and $\Upsilon _C$ are homological equivalences associated with $B \cap C$, B and C; a short exact sequence $((B \cap C), (B \oplus C), A = (B \cup C), i, j, r, s)$ can be defined⁵, and a homological equivalence associated with A can be computed by applying the SES theorem.

More basic operations are studied here: cone and identification (cf. [3] for more precisions). Cone(A), the cone of A, consists in adding a new 0-simplex v to A, and, for each i-simplex $\sigma$, in adding a $(i+1)$-simplex incident to $\sigma$ and v. Obviously, a homological equivalence $\Upsilon : (Cone(A)) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (Cone(A)) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (X)$ can be defined, where X contains only one 0-dimensional generator (the homology of a cone is trivial), and $\Upsilon$ can be computed in linear time according to the size of A.

The basic identification operation $Ident(A,\sigma ,\tau )$ consists, given two i-simplices $\sigma$ and $\tau$ having the same boundary, in replacing them by a new simplex $\mu$ such that the boundary (resp. the star) of $\mu$ is the boundary of $\sigma$ (resp. the union of the stars of $\sigma$ and $\tau$). This operation can be easily generalized in order to identify any two i-simplices, and more generally subsets of simplices.

Assume a homological equivalence $\Upsilon : (A) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (A^{B}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (A^{S})$ is associated with A. Given a set of simplices $A^0$ which have to be identified, a chain complex $(A^0)$ can be computed, in which each i-dimensional generator corresponds to a basic identification of i-simplices (i.e. if k i-simplices are identified into one i-simplex, there are $(k-1)$ corresponding i-generators in $(A^0)$). The boundary operator of $(A^0)$ is deduced from the face operators of the simplices of $A^0$. So, a homological equivalence $\Upsilon ^0: (A^0) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (A^{0}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (A^{0})$ can be computed in linear time according to the size of $A^0$ (the size takes into account the simplices of $A^0$ and their face operators). A better homological equivalence $\Upsilon '^0: (A^0) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (A^{0}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (A'^{0})$ may be deduced by applying a method for simplifying $(A^0)$, i.e. which computes a reduction $(A^0) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (A'^0)$.

Let $Ident(A,A^0)$ be the result of the identification of the simplices of $A^0$ in A. It is possible to compute a short exact sequence $Q = ((A^0), (A), (Ident(A,A^0)),$ i, j, r, s) in linear time according to the size of A. Thus, by applying the SES theorem, it is possible to compute a homological equivalence $\Upsilon ^I: (Ident(A,A^0))$ $\Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (I^{B}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (I^{S})$ (cf. Fig. 1). Once again, a better homological equivalence $\Upsilon '^I: (Ident(A,A^0)) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow (I^{B}) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (I'^{S})$ may be deduced by applying a method for simplifying $(I^S)$, i.e. which computes a reduction $(I^S) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow (I'^S)$. Then, the homology of $Ident(A,A^0)$ can be computed from $(I'^S)$.

As said before, the homological equivalence $\Upsilon ^0$ can be computed in linear time according to the size of $A^0$, and the short exact sequence Q can be computed in linear time according to the size of A. The generators of $(I^B)$ (resp. $(I^S)$) are the generators of $(A^0)$ and of $(A^B)$ (resp. $(A'^0)$ and $(A^S)$; this explains why it is interesting to reduce $(A^0)$ into $(A'^0)$). It is not possible to give a precise evaluation of the complexity related to the computation of the boundary operators of $(I^B)$ and $(I^S)$, and of the mappings of $\Upsilon ^I$, since this complexity depends on $\Upsilon$, and thus depends also on the operations previously applied for constructing A. But the complexity can be evaluated for certain cases: for instance, when A is constructed by applying identifications, the whole computation is linear; moreover, if $(I^B)$ (resp. $I^S$) is deduced by modifying $(A^B)$ (resp. $(A^S)$), the computation is sub-linear; and the complexity of the whole construction (i.e. related to all computations for all steps) is linear according to the size of the initial object. In the general case, the complexity of the computation is clearly related to the size of the parts of the object which are identified, i.e. $(A^0)$.

An informal argument for the interest of the approach is the fact that, for many construction processes, local operations are applied at each construction step; since the complexity is related to the modified parts, it is interesting to modify a previously known homological information rather than to compute it from scratch. Other precisions are given in Section 3 and Appendix 6.7 in [3]. In particular, note that the SES theorem applies for the inverse operation of the identification.

Fig. 1.

Incremental computation of homological equivalences

At last, note that these results generalize in some sense the results described in [5, 6], since the identification operation is a more basic operation than the gluing of connected components. In other words, gluing connected components can be achieved by identifying parts of their boundaries; but the identification operation can also be applied to subsets of simplices belonging to the same connected component.

4 Application to Cellular Structures

The previous results directly apply to other structures, as cubical [8] and simploidal [12] structures (as for simplices, the homology of any cube or simploid is trivial; moreover, classical results apply for the cartesian product, which corresponds in some way to the cone for simplicial objects). They can also be applied to cellular combinatorial structures as incidence graphs⁶ [10] and combinatorial maps [7]. An incidence graph is represented in Fig. 2; results in [3] are obtained for combinatorial maps, which generalize incidence graphs in order to take multi-incidence into account⁷, and these results directly apply to incidence graphs.

Any cellular combinatorial structure can be constructed by applying two basic operations: extension and identification. Given a connected n-dimensional structure, in which the dimension of all main cells is n, the extension consists in adding a new $(n+1)$-cell incident to all n-cells. For instance, this operation applied to the incidence graph in Fig. 2 adds a volume incident to faces $f_1$ and $f_2$, the resulting “corresponding object” is a 3-ball. The identification operation consists in “merging” two cells having the same boundary; as for the simplicial case, this operation can be generalized in order to identify subsets of cells (this is constrained by the fact that two cells can be identified if they are isomorphic: for instance, it is not possible to identify a triangle and a square).

Fig. 2.

A 2-sphere, subdivided into 2 faces, 2 edges and 2 vertices, together with its simplicial equivalent and the corresponding incidence graph.

In the general case, it is not possible to associate a “cellular” chain complex (A) with any cellular combinatorial structure A, i.e. a chain complex in which any generator corresponds to a cell, and such that the homology of (A) is the homology of A. It is thus not possible to directly apply the results obtained in the simplicial case to cellular combinatorial structures. Indeed, cellular combinatorial structures exist, in which cells cannot be associated with balls. For instance, applying the extension operation to an incidence graph which corresponds to a subdivided torus or a Klein bottle does not produce a 3-ball. Moreover, any $(n+1)$-cell can be defined as the result of the application of the extension operation to a n-dimensional cellular combinatorial structure; but we do not know how to decide in the general case whether a (simplicial or cellular) combinatorial structure corresponds to a n-sphere. So, we do not know how to decide in the general case whether a combinatorial cell corresponds to a ball.

But it is always possible to associate a simplicial equivalent S(A) with any cellular combinatorial structure A; so, it is always possible to associate a “simplicial” chain complex (S(A)) with any cellular combinatorial structure A, i.e. a chain complex in which any generator corresponds to a simplex of S(A), and such that the homology of (S(A)) is the homology of A. So, the results presented in Sect. 3 can be directly applied, by maintaining at each step of the construction of A its simplicial chain complex (S(A)). The problem here is the complexity of the approach, since it is possible that many simplices in S(A) are associated with one cell in A. So, more efficient approaches have been investigated.

4.1 A Subclass of Cellular Combinatorial Structures

A subset of cellular combinatorial structures has been defined in [2] (cf. also [4]): each structure A of this subclass satisfies properties so that the cellular chain complex (A) is homologically equivalent to the simplicial chain complex (S(A)). So, the results presented in Sect. 3 can be directly applied to the structures of this subclass, associated with their corresponding cellular chain complexes, but it is necessary to check at each construction step whether the properties of the subclass are still satisfied (this control can be done easily without significative cost, due to the definition itself of the properties).

4.2 The General Case

The properties characterizing this subclass are sufficient but not necessary to ensure the equivalence between (A) and (S(A)). Moreover, it may be useful for some constructions to ignore these properties, even if only temporarily. It can thus be useful to handle A and (S(A)), even if it is less efficient than to handle A and (A). Even in this case, it is possible to optimize the computations. Indeed, the interior of each cell c in A corresponds to a subset of simplices in S(A); a homological equivalence $\Upsilon ^c$ can be associated with the interior of c when it is created, and it is possible to maintain $\Upsilon ^c$ during the construction process in order to optimize the homology computation.

More precisely, assume a homological equivalence is associated with the interior of any cell and with any connected component. Assume c is created by an extension operation applied to a connected component C of A. This operation corresponds in S(A) to a cone operation applied to S(C), where the vertex v of the cone symbolizes cell c (in fact, the interior of c corresponds to the subset incident to v, so the structure of the interior of c is very close to the structure of S(C), since c corresponds to a cone on S(C)). Each cell of C remains unchanged, so its homological equivalence is unchanged; the homological equivalence associated with the connected component after operation is trivially defined, since the resulting connected component is a cone; the homological equivalence associated with c can be easily deduced from the homological equivalence associated with C by applying the perturbation lemmas (cf. [13] pages 48–49). All computations can be performed in linear time according to the size of S(C). Note that, at last, some reduction process may be applied to the small chain complex of $\Upsilon ^c$.

Let $Ident(A,A^0)$ be the result of the identification of cells of a subset $A^0$ in A. Let c be a cell of $Ident(A,A^0)$: either c does not result from the identification of cells, and its homological equivalence $\Upsilon ^c$ is not modified; either it results from the identification of isomorphic cells, and $\Upsilon ^c$ is simply a homological equivalence associated with one of these identified cells (all these homological equivalences are homologically equivalent, since the cells are isomorphic): so, nothing is really computed.

The homological equivalence associated with $S(Ident(A,A^0))$ is computed in the following way. A homological equivalence $\Upsilon ^1_{A^0}$ is computed as the direct sum of homological equivalences corresponding to the identified cells; more precisely (and as for the simplicial case), if k isomorphic i-cells $\{c_j\}_{j \in [1,k]}$ are identified into one cell, there are in $\Upsilon ^1_{A^0}$ $k-1$ copies of $\Upsilon ^{c_j}$, for some $j \in [1,k]$ (for instance, j may be chosen according to the complexity of $\Upsilon ^{c_j}$). It is now possible to deduce from $\Upsilon ^1_{A^0}$ a homological equivalence $\Upsilon ^2_{A^0}$ by “linking” the homological equivalences corresponding to cells accordingly to the boundary relations between cells in A; this can be done by applying the perturbation lemmas (cf. [13] pages 48–49), and the complexity is linear according to the size of $\Upsilon ^1_{A^0}$ and n, where n is the highest dimension of a cell in $A^0$. Then, a reduction process can be applied to the small complex of $\Upsilon ^2_{A^0}$, producing $\Upsilon ^0: C(A^0) \Leftarrow \!\!\!\!\Leftarrow \!\!\!\!\Leftarrow C^B(A^0) \Rightarrow \!\!\!\!\Rightarrow \!\!\!\!\Rightarrow C^S(A^0)$.

Moreover, a short exact sequence $Q = (C(A^0), (S(A)), (S(Ident(A,A^0))),$ i, j, r, s) can be computed in linear time according to the size of S(A) (as for the simplicial case, the complexity of the computation of the “interesting” information is sub-linear). The SES theorem can then be applied in order to deduce a homological equivalence $\Upsilon ^I$ associated with $Ident(A,A^0)$; as for the simplicial case, a reduction process can be applied to the small complex of $\Upsilon ^I$, and a “better” homological equivalence $\Upsilon '^I$ can be deduced.

As for the simplicial case in Sect. 3, similar remarks about the complexity of the process can be done (the main difference with the simplicial case is the complexity of the computation of $\Upsilon ^0$, which depends also on the dimension of the identified cells). At last, note that a similar process can also be applied for the inverse of the identification operation.