Pricing Shared-Loss Hedge Fund Fee Structures

Abstract

The asset management business is driven by fee structures. In the context of hedge funds, fees have usually been a hybrid combination of two different types, which has coined a well-known business term of “2 and 20”. As an attempt to provide better alignment with their investors, in a new context of low interest rates and lukewarm performance, a new type of fund fees has been introduced in the last few years that offers a more symmetric payment structure, which we will refer to as shared loss. In this framework, in return for receiving performance fees, the fund manager provides some downside protection against losses to the investors. We show that the position values of the investor and the hedge fund manager can be formulated as portfolios of options, and discuss issues regarding pricing and fairness of the fee rates, and incentives for both investors and hedge fund managers. In particular, we will be able to show that, from a present value perspective, these fee structures can be set up as being favorable either to the hedge fund manager or to the investor. The paper is based on an arbitrage-free pricing framework. However, if one is to take into account the value to the business that investor capital brings to a fund, which is not part of our framework, it is possible to create a situation where both investors as well as asset managers win.

This research was supported in part by the Natural Sciences and Engineering Research Council of Canada.

1 Introduction

Hedge Funds are pooled investment vehicles overseen by a management company. They generally aim at absolute return portfolios and their success is usually linked to market inefficiencies, such as instrument mispricing, misguided market consensus or, in general terms, the manager’s intelligence to anticipate market moves. The nature of these investments is that they exploit investment opportunities that are rare. This is a characteristic that they share with private equity investments, but they share with the mutual fund industry the fact that they often trade in liquid, marketable securities. Fund sizes are more in line with private equity investing than with the mammoth mutual fund industry. Their compensation structure, because of their limited access to opportunity, is also more in line with the private equity universe, and usually consists in a fixed, asset-based fee, and a variable, performance fee base. Because of market conditions that have been in place over the last several years, in particular the low interest rate environment, coupled with the lukewarm performance of the hedge fund sector in the recent years, investors have become increasingly more sensitive to fee structures. The traditional 2&20 fee structure, consisting of a flat fee of 2 % of assets under management together with a performance fee of 20 % of net profits is considered unfair on the basis of the asymmetry: the management company will always earn a fee, whereas the investor is only guaranteed to pay that fee. The advent of the 40-ACT funds¹ has, in particular, dispensed with the performance fee base in favor of a fixed management fee, which is more in line with the mutual fund industry than with the hedge fund industry. This compensation model essentially rewards funds for becoming asset gatherers instead of the alpha-seeking business the hedge fund was set out to be. In this paper we will examine, from a quantitative perspective, a suite of symmetric performance fee structures which are gaining traction with more sophisticated investors, known as first-loss (or shared-loss) fee structures. In this new framework, in return for receiving performance fees, the fund manager provides some downside protection against losses to the investors.

The issue of the incentives created by hedge fund fees bears much similarity to issues surrounding the structure of executive compensation. At first glance, the optionality inherent in both would seem to incentivize greater risk taking. However, the reality is more subtle. Carpenter [2] studies the case of executive compensation, when the manager cannot hedge options provided as compensation by trading the underlying. In certain conditions, a utility-maximizing manager may choose to reduce rather than increase the volatility of the underlying firm. Ross [9] gives necessary and sufficient conditions for a fee schedule to make a utility-maximizing manager more or less risk-averse. Hodder and Jackwerth [6] consider the effects of hedge fund fee incentives on a risk manager with power utility, and also in the presence of a liquidation barrier. They find that over a one-year horizon, risk-taking varies dramatically with fund value, but that this effect is moderated over longer time horizons. Kouwenberg and Ziemba [7] consider loss-averse hedge fund managers and find that higher incentive fees lead to riskier fund management strategies. However, this effect is reduced if a significant portion of the manager’s own money is invested in the fund. They further provide empirical evidence showing that hedge funds with incentive fees have significantly lower mean returns (net of fees), and find a positive correlation between fee levels and downside risk. They find that risk is increasing with respect to the performance fee if the manager’s objective function is based on cumulative prospect theory, rather than utility, and provide empirical evidence. Recent work on the analysis of hedge fund fee structures includes that of Goetzmann et al. [3], who value a fee structure with a highwater mark provision, using a PDE approach with a fixed investment portfolio, Panageas and Westerfield [8], who consider the portfolio selection decision of maximizing the present value of fees for a risk-neutral manager over an infinite horizon, and Guasoni and Obłój [4], who extend this work to managers with risk-averse power utility. Closest to the current work is He and Kou [5], who analyze shared-loss fee structures for hedge funds by looking at the portfolio selection decision of a hedge fund manager whose preferences are modeled using cumulative prospect theory. The problem is considered in the presence of a manager investing in the fund, and with a predetermined liquidation barrier. Analytical solutions of the portfolio selection problem are provided, and the result (cumulative prospect theory) for both the investor and the manager is examined. It is found that depending on the parameter values, either a traditional fee structure or a first-loss fee structure may result in a riskier investment strategy. While for some parameter values, the first-loss structure improves the utility of both the investor and the hedge fund manager, they find that for typical values, the manager is better off, while the investor is worse off. In this paper, we investigate the shared-loss fee structures from the perspective of risk-neutral valuation, with no further assumptions about investor preferences, while He and Kou [5] solve the stochastic control problem (under the real-world measure) corresponding to the manager maximizing the utility function from cumulative prospect theory, and also evaluate the investor’s payoff using the same type of criterion.

The paper is organized as follows. First, we will review the traditional fee structures in some detail. Next, we will introduce the notion and mechanics of the first-loss structures, and a framework for a fee pricing based on the theory of option price valuation. After that, we will introduce the concept of net fee, a number that will allow us to determine whether the investor or the management company is the net winner in a given fee agreement. Finally, we will present a set of computational examples that will display the net fee as a function of the agreement and market variables.

2 Hedge Fund Fees

The hedge fund manager charges two types of fees to the fund investors:

• A fixed management fee, usually ranging from 1 % to 2 % of net asset values.

• A performance fee, most commonly equal to 20 % of net profits obtained by the fund.

In this paper we assume a single investor and a single share issued by the fund. The extension to the case of multiple investors and multiple shares is straightforward. Although fees are paid according to a determined schedule (usually monthly or quarterly for management fees and annual for performance fees), we will assume a single payment at the end of a fixed term T.

The fund value evolution and fee payment mechanics are denoted as follows: the initial fund supplied by the investor is $X_0$. The hedge fund manager then invests fund assets to create future gross values $X_t$, for $t>0$. The gross fund value $X_t$ is split between the investor’s worth $I_t$ (the net asset value) and the manager’s fee $M_t$:

$$ X_t=I_t+M_t. $$

At time 0, $X_0=I_0$ and $M_0=0$.

There are countless variations to this basic framework, including hurdles, clawbacks, etc. (for more details on first-loss arrangements see Banzaca [1]). We will ignore those and assume the commonly used version of a management fee equal to $m\cdot X_0$ (m represents a fixed percentage of the initial investment by the investor), and a performance fee of

$$ \alpha \cdot \left( X_T-(1+m)X_0)\right) _+, $$

payable only when it is positive, and equal to zero when it is negative. Hence,

$$\begin{aligned} \begin{aligned} M_T&=m\cdot X_0 + \alpha \cdot \left( X_T-(1+m)X_0)_+\right) \\ \end{aligned} \end{aligned}$$

(1)

In other words, while the management fee is a fixed future liability to the investor, the performance fee is a contingent claim on the part of the manager. As a consequence, we will be pricing the management fee simply as a fixed guaranteed fee with a predetermined future cash value, and we will be valuing the performance fee as the value of a certain call option. In our setting, we will assume normally distributed log-returns for the invested assets $X_t$, which allows us to value the performance fee in the Black–Scholes framework. It is worth mentioning that hedge funds managers can speculate on volatility, credit risks, etc. and in contrast to the traditional money managers, they can go long and short. The diversity in investment styles and the different levels of gross and net exposure that they can employ could result in leptokurtic (non-normal) properties in their returns, which is revealed through frequent large negative returns to the left of the return distribution. Generalization of the current framework to models that account for non-normality of the hedge fund returns, for example by employing generalized autoregressive conditional heteroskedasticity (GARCH) models, could be a subject for future research.

3 The First-Loss Model

Calpers announced in 2014 that they were exiting hedge fund investments WSJ [10]. While not the main stated reason for their decision, one they mentioned was high fees payable to their hedge fund managers, something that has caught the attention of investors worldwide in the contemporary context of a widely accepted notion that hedge fund fees nowadays are too high. Certain hedge funds are reacting to this shifting balance of power between the sell-side and the buy-side of the investment business with the creation of innovative fee structures which still reward the intellectual capital of the hedge fund manager and allow for business growth but at the same time offer the investor a more symmetric compensation structure.

An example of a first-loss structure is the following:

• The investor provides an investment of $100M to a fund.

• The fund manager will absorb the first-loss up to 10 % of the initial investment.

• The investor pays a management fee of 1 % to the manager, and performance fee of 50 %.

In our paper we will present a quantitative comparison of the fees payable to the manager and the risk-neutral valuation of the guarantee offered to the investor. We want to note, for the sake of completeness, that there are many other qualitative considerations which are relevant when analyzing both the fee structure as well as the business value offered to a management company by the investor, which are not the objective of this paper. In fact, hedge fund start-ups have become more difficult in recent times, increasing value to any investor action that allows a hedge fund business to succeed. That value is linked to a wide variety of fund characteristics, including the size of assets under management (AUM), the track record, or historical performance, and the reputation of its investor base, among others.

In addition to the initial investment $X_0$, the management fee m and the performance fee $\alpha$, payable at a fixed time horizon T, we will now also consider a deposit amount c, as a percentage of the initial investment $X_0$, which the manager will provide as a guarantee for losses. Our objective is to analyze the relationship between all four variables to determine whether the investor, or the manager, is the net winner of value-add from a risk-neutral valuation perspective.

4 An Option Pricing Framework

The fund value $X_t$ is split between the investors $I_t$ and the manager $M_t$, where, $X_t=I_t+M_t.$ In the following sub-sections we derive the payoff function of each player separately, and then price the positions accordingly.

4.1 Payoff to the Investor

The payoff to the investor at the terminal time T is:

$$ I_T= {{\left\{ \begin{array}{ll} X_T - mX_0 - \alpha (X_T - m X_0 - X_0) &{} \hbox {when} \; X_T - m X_0\ge X_0 \\ X_0 &{} \hbox {when}\; (1-c)X_0\le X_T - m X_0\le X_0 \\ X_T+(c-m)X_0 &{} \hbox {when}\; X_T - m X_0\le (1 - c) X_0 \\ \end{array}\right. }} $$

or, writing the payoff in a more compact form:

$$ { \begin{matrix} I_T=&{}X_T-mX_0 &{}\hbox {(pays a management fee)} \\ &{}-\alpha (X_T - m X_0 - X_0)_+ &{}\hbox {(pays a performance fee)} \\ &{}+(X_0-X_T + m X_0)_+-((1-c)X_0-X_T + m X_0)_+ &{}\hbox {(receives a guarantee)} \\ \end{matrix} }$$

Thus, we see that the position of the investor is equivalent to the following portfolio:

• A position in the hedge fund assets, with initial investment $X_{0}$, less management fee, that is, $X_{0} - m X_0$.

• A short position in $\alpha$ call options on the hedge fund assets, with strike price $X_0 + m X_0$ (the performance fee, or performance call option, given to the hedge fund manager).

• A long position in a put option on the fund assets, with the strike price $X_0 + m X_0$ (the insurance put option).

• A short position in a put option on the fund assets, with strike price $(1-c)X_{0} + m X_0$ (yielding a cap on the insurance payment).

4.2 Payoff to the Manager

The payoff to the manager is $M_T = X_T - I_T$. In other words, the payoff to the hedge fund manager results from the manager having the opposite position in all of the options of the investor. More explicitly,

$$ { \begin{matrix} M_T=&{}mX_0 &{}\hbox {(receives a management fee)} \\ &{}+\alpha (X_T - m X_0 - X_0)_+ &{}\hbox {(receives a performance fee)} \\ &{}-(X_0-X_T + m X_0)_++((1-c)X_0-X_T + m X_0)_+ &{}\hbox {(provides a guarantee)} \\ \end{matrix} }$$

which implies that the hedge fund manager has a portfolio of options consisting of:

• A constant position in the fixed management fee of $m X_{0}$.

• A long position in $\alpha$ call options on the hedge fund assets, with strike price $X_0 + m X_0$.

• A short position in a put option on the fund assets, with the strike price $X_0 + m X_0$.

• A long position in a put option on the fund assets, with strike price $(1-c)X_{0} + m X_0$.

Note that net income to the management company is now no longer guaranteed to be positive. In addition, since the options trades constitute a zero-sum game (the positions of the manager and the investor are opposite each other), the sum of the investor payoff and the manager payoff is equal to $X_T$.

4.3 Valuation: Pricing Fees as Derivatives

In this section, we will value the positions of the investor and the hedge fund manager using a simple Black–Scholes model for the underlying fund value process. In particular, we employ risk-neutral valuation, and assume that under the risk-neutral probabilities, the fund value process satisfies the stochastic differential equation:

$$\begin{aligned} dX_t=rX_t\,dt\;+\;\sigma \,X_t\,dW_t, \end{aligned}$$

(2)

with solution:

$$\begin{aligned} X_{t} = X_{0} \exp \left( (r-\tfrac{\sigma ^{2}}{2})t + \sigma W_{t}\right) \end{aligned}$$

(3)

where $W_{t}$ is a standard Brownian motion, and r and $\sigma$ are positive constants, giving the continuously compounded risk-free interest rate and the volatility of the hedge fund assets respectively. It should be noted that the Black–Scholes framework is applicable to our context as the underlying, that is the fund value, can be dynamically traded. Moreover, in a managed account context, even the liquidity of the fund can be made to match the liquidity of the underlying traded securities.

The Black–Scholes formula can be used to derive the price of the investor’s position under the Black–Scholes model:

$$\begin{aligned} V_{I}(0)= & {} X_{0} - e^{-r T} m X_0 - \alpha C(X_0,T,X_0 + m X_0,r,\sigma ) \nonumber \\&+ P(X_0,T,X_0 + m X_0,r,\sigma )-P(X_0,T,(1-c)X_0 + m X_0,r,\sigma ) \end{aligned}$$

(4)

where $C(X,T,K,r,\sigma )$ is the Black–Scholes price of a call option on a non-dividend paying asset with current value of the underlying X, time to expiration T, strike price K, risk-free interest rate r and volatility $\sigma$, and $P(X,T,K,r,\sigma )$ is the Black–Scholes put option price with the same parameters as arguments.

5 Consequences of the Derivative Pricing Framework

5.1 Graphical Analysis

To compare and contrast the traditional and shared-loss fee structures, in our base case we take the investment horizon to be one month, that is $T = 1/12$, the performance fee $\alpha = 50\,\%$, the manager deposit $c = 10\,\%$, the risk-free interest rate $r = 2\,\%$, the volatility $\sigma =15\,\%$, and the initial investment $X_0 = \$1$. For simplicity and without loss of generality we assume a zero management fee for our base case.

With our base case parameters, the total value of the investor’s payoff is 1.0073, and the value of the manager’s payoff is $-0.0073$. Notice that the value of the investor’s payoff is greater than the initial investment of 1. In contrast, the price of the traditional investor payoff (without the insurance part of the payoff—i.e. removing both put options) is 0.9909, and the value of the manager’s payoff in this instance is 0.0091.

5.1.1 Payoff Functions of the Investor and the Manager

The payoff functions of the investor under the shared-loss and the traditional fee structures are given in Fig. 1. The payoff to the hedge fund manager using the aforementioned benchmark values and under the shared-loss fee structure is also depicted in Fig. 2 along with the traditional payoff structure with only the performance fee $\alpha (X_{T}-X_{0})_+$. Observe that since the options trades constitute a zero-sum game (the positions of the manager and the investor are opposite each other), the sum of the investor payoff and the manager payoff is equal to $X_{T}$.

Fig. 1

Payoff for the hedge fund investor

Fig. 2

Payoff for the hedge fund manager

Fig. 3

Fair performance fee versus volatility

Fig. 4

Fair performance fee versus normalized (by deposit) volatility

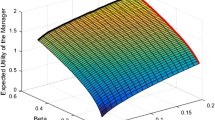
Figure 3 illustrates the ‘fair performance fee’, where investor gets a payoff with present value equal to his initial cash injection, $X_0$, given volatility and manager’s deposit levels, i.e. we set $V_I(0) = X_0$. The fair performance fee can be easily obtained from Eq. (4) as,

$$\begin{aligned} \alpha _{\text{ fair }} = \frac{- e^{-r T} m X_0 + P(X_0,T,X_0 + m X_0,r,\sigma ) - P(X_0,T,(1-c)X_0 + m X_0,r,\sigma )}{C(X_0,T,X_0 + m X_0,r,\sigma )} \end{aligned}$$

Interested reader can derive explicit, well-known expressions for the sensitivities of the $\alpha _{\text {fair}}$ relative to different parameters in terms of the Greeks and Vega of the involving options. As can be seen from the figure, for small values of volatility, the fair performance fee is indifferent to the levels of manager’s deposit; however, as volatility increases, a higher level of deposit by the manager translates into a higher performance fee paid by the investor to make the deal a fair one. In Fig. 4, we normalize the volatility on the horizontal axis by the manager’s deposit defined as a percentage of the initial investment $X_0$. For a given level of deposit, the higher the volatility of the underlying investment, the higher the probability that the loss incurred by the manager exceeds the deposit. In other words, the probability that the manager exercises the put option offered by the investor increases, which results in a reversal in the fair performance fee for higher levels of volatility. This is clearly illustrated in Fig. 4 where volatility and deposit are combined in a single scaling variable, that is, volatility/deposit, where the deposit is expressed as a percentage of the initial investment $X_0$. The corresponding maximum value for the fair performance fee increases with the size of the deposit; that’s because for higher deposits, the manager will have to lose more and more before the investor starts bearing the residual loss, therefore his compensation should be higher accordingly. Note that the x-axis in Figs. 3 and 4 is incorporating the annual volatility of the fund assets; however, the performance fee is crystallized on a monthly basis which suggests a comparison between the deposit level and monthly volatility, as opposed to annual volatility. Since returns are assumed to follow a normal distribution in our Black–Scholes framework, one can explicitly calculate the probability of the returns falling into a certain interval, in particular, with about 68 % probability, the return falls within 1 standard deviation of the mean. This explains why the curves for various deposits reach a maximum roughly around the same level of (annual) volatility/deposit ratio, in the [1, 2] interval.

5.2 Sensitivity Analysis

In this section, we perform a sensitivity analysis of the prices of the investor’s and manager’s payouts, as a function of the different model parameters.

Fig. 5

Value of the investor’s position versus volatility $\sigma$

5.2.1 Volatility ($\sigma$)

Figure 5 shows the value of the investor’s position as a function of the volatility parameter $\sigma$, as $\sigma$ ranges from $5\,\%$ to $60\,\%$.

We see that the position is initially an increasing function of the volatility, owing to the increasing value of the investor’s put option as a function of $\sigma$. However, as the volatility becomes very large, the value of the investor’s position starts to decline as the hedge fund’s call option, as well as its put option, become more valuable. The maximum value for the investor occurs at a volatility around $\sigma =32.5\,\%$. Observe however, that the value is relatively insensitive to the level of $\sigma$, with a minimum value of 1.0016, and a maximum value of 1.0118.

5.2.2 Manager Deposit (c)

We varied the manager deposit between $1\,\%$ and $25\,\%$, while holding all other parameters at their base case values. The results of the sensitivity analysis are shown in Fig. 6.

Fig. 6

Value of the investor’s position versus manager’s deposit c

As would be expected, the value of the investor’s position is an increasing function of the manager’s deposit. The value of the position is equal to one (break-even point, or ‘fair fee point’) at around $c=0.0233$. Any deposit level less than $c=0.0233$ puts the investor at a disadvantage, and the investor is indifferent to deposit levels higher than $10\,\%$.

5.2.3 Maturity Date (T)

The dependence on the time to maturity is of interest specially when adapting the results of this paper to realistic situations. As we mentioned earlier, our mathematical assumption is that fees will be paid at a fixed time in the future. In practice, fees are payable according to calendars agreed between the investors and the manager. In the graphs that follow, we address this by varying the expiration date T from 1 day to 1 year. The results are shown in Fig. 7.

Fig. 7

Value of the investor’s position versus the expiration date T

Initially, the value of the position is increasing in T, but eventually, it begins to decrease in T, as the options given to the hedge fund manager become more valuable. The maximum value of the investor’s position occurs at T around one quarter of a year ($T\sim 0.22$).

6 Conclusion

The exchange of business value between the manager and the investor is always a complex one: beyond fees paid, there are intangibles the investor gives the manager. An asset management business is valued taking into account many factors, such as track records, years in business, assets under management, the reputation of its investors, and of course fees. In this paper we focus on first-loss fee structures, which are bringing novel points of attention between investors and hedge fund managers in the historical discussions on fair compensation. We focus only on the fee payable by the investor and the guarantee offered by the manager, which is the main novelty in this set up. The main challenge in this new paradigm is to evaluate the value of the guarantee offered by the hedge fund manager in relation to the fee paid by the investor. In this paper, we developed a mathematical approach to compare the two features of guarantee and performance fee from an option pricing perspective. The framework is flexible and can be used for different specific investment settings and can account for slight variations from one fund to another. Our salient leitmotif is: fee agreements must be structured to be attractive to managers so they are willing to participate, and at the same time provide a cushion against losses to the investor. A significant contribution, that sheds light on the road-map and paves the way for deeper investigations, is to see, and more importantly formulate, the underlying fee structure from the lens of option valuation. By employing a risk-neutral framework and options pricing theory, one is able to not only price, but also analyze the sensitivity of the value of the investor’s and manager’s positions in reference to a set of influential parameters.