Tracking a Human Fast and Reliably Against Occlusion and Human-Crossing

Abstract

Tracking a human using the computer vision techniques is essential in the automatic surveillance task. Not only its accuracy and speed but also how it deals with occlusion and human-crossing are the challenges for a reliable tracking framework. Among many, Kernelized Correlation Filter (KCF) has become a state-of-the-art tracker partly because of its high speed, although its performance in dealing diverse situations requires some improvement. We present a new tracking method whereby the reliability is greatly enhanced while maintaining its speed by integrating a Kalman filter with the KCF. The tracker works as follow. After the KCF estimates target’s position based on the prediction by the Kalman filter, then the estimated value is given to the updating step of the Kalman filter. During the KCF learning phase, the kernel model is updated using the correct state. Evaluation result using the standard tracking databases suggests that the present tracker outperforms the standard KCF, MOSSE and MIL trackers, respectively. In particular, it is the only tracker that can deal very well with the occlusion and human-crossing tasks, which are the crucial requirements for the high-end surveillance.

1 Introduction

Human tracking has played an important role in the automatic surveillance system [15]. Currently, surveillance [7, 13] is contributing vital roles not only in the research but also in the market. Visual tracking is the process of estimating the trajectory of an object in the image plane as it moves around in the scene. According to [15], tracking objects can be complex due to its accuracy and speed as well as how it deals with occlusion and human-crossing cases. Numerous approaches for object tracking have been proposed. Among them, Kernelized Correlation Filter [5, 6] has been a state-of-the-art tracker partly because of its high speed and simple implement with only a few lines of code. It is the third performing tracker among many in term of accuracy [10]. And yet, its performance in dealing such occlusion requires some improvement for robust tracking.

In general, a Kalman filter estimates the state of a linear system where state is supposed to be distributed by a Gaussian [2, 8, 12, 15]. It is known that the Kalman filter successfully tracks objects even in the case of occlusion if the assumed type of motion is correctly modeled [2]. This assumption is very strict and it is only suitable for tracking very small objects [15].

Combination of Kalman filter with the kernel method has also been proposed based upon the mean-shift tracking [9, 11, 17, 18]. The mean-shift tracker eliminates the brute force search in the standard template matching and shortens the computation time although it requires that a portion of the objects should be inside a circular region during the initialization stage [15].

In this paper we present a new tracking method whereby the reliability is greatly enhanced while the speed is also maintained by combining a Kalman filter with the KCF. Once KCF estimates a target position based on the prediction by the Kalman filter, the estimated value becomes the observation in updating the object’s state. During the KCF learning phase, the correct state of the Kalman filter is utilized to update the kernel model. However, when the tracker meets an occlusion, the Kalman filter omits observation values from KCF and adjusts the state based on the previous state. Experimental results show that the present tracker outperforms the standard KCF, MOSSE (Minimum Output Sum of Squared Error) [1] and MIL (Multiple Instance Learning) trackers [16], respectively. In particular, it is the only tracker that can deal very well with occlusion and human-crossing task, which are critical requirements for the high-end surveillance task.

The rest of the paper is organized as follows. In Sects. 2 and 3, we review the Kernelized Correlation Filter and Kalman Filter, respectively. In Sect. 4, we describe our proposed tracker in detail. In Sect. 5, we present experimental results. Finally, Sect. 6 summarizes this paper.

2 Kernelized Correlation Filters

2.1 Circulant Matrices

KCF trains a linear classifier using both a base sample, i.e. a positive example, and several virtual samples, which serve as the negative examples, obtained by translating it. Here, a cyclic shift operator is utilized in modeling this translation. Because of the cyclic property [4], the signal x becomes identical after $n^{th}$ shifts, and the full set of shifted signals is

$$\begin{aligned} \left\{ P^{u}x | u=0, ..., n-1 \right\} \end{aligned}$$

(1)

with P is the permutation matrix [5] and n is the number of translation step.

Element of Eq. (1) is a row of a circulant matrix X

$$\begin{aligned} X = C(x) = \begin{bmatrix} x_{1}&x_{2}&x_{3}&...&x_{n} \\ x_{n}&x_{1}&x_{2}&...&x_{n-1}\\ x_{n-1}&x_{n}&x_{1}&...&x_{n-2}\\ .&.&.&.&. \\ .&.&.&.&.\\ .&.&.&.&. \\ x_{2}&x_{3}&x_{4}&...&x_{1} \end{bmatrix} \end{aligned}$$

(2)

Since all circulant matrices are made diagonal by the discrete Fourier transform (DFT) [4], X can be expressed as

$$\begin{aligned} X = F diag(\hat{x})F^{H} \end{aligned}$$

(3)

where F is Discrete Fourier transform (DFT) matrix, and $\hat{x}$ is the DFT of the generating vector.

Equation 3 expresses the eigendecomposition of a general circulant matrix and why KCF is fast when it is implemented.

2.2 Fast Kernel Regression

The kernel matrix K (n x n) stores the dot-products between all pairs of samples

$$\begin{aligned} K_{ij} = \kappa (x_{i}, x_{j}) = \varphi ^{T} (x_{i}) \varphi (x_{i}) \end{aligned}$$

(4)

with high-dimensional space $\varphi (.)$.

The following kernels satisfy the condition to claim that K is circulant [6]:

• Radial Basic Function kernels –e.g., Gaussian.

• Dot-product kernels –e.g., linear, polynomial.

• Additive kernels –e.g., intersection, $\chi ^{2}$ and Hellinger kernels.

• Exponentiated additive kernels.

Therefore, the kernelized version of Ridge Regression is possible to diagonalize

$$\begin{aligned} \hat{\alpha }^{*} = \frac{\hat{y}^{*}}{\hat{k}^{xx} + \lambda } \end{aligned}$$

(5)

where $K = C(k^{xx})$ is kernel matrix.

Learning phase utilizes Eq. (5) to update the model for next frame.

2.3 Fast Detection

Several candidate patches, z, that can be modeled by cyclic shifts are evaluated by the regression function f(z). To compute efficiently, detection phase diagonalizes regression function

$$\begin{aligned} \hat{f}(z) = \hat{k}^{xz} \odot \hat{\alpha } \end{aligned}$$

(6)

where $k^{xz}$ is a kernel correlation of x and z.

During detecting phase, Eq. (6) predicts where is the center of target within the given frame with a learned coefficients $\alpha$.

2.4 Fast Kernel Correlation

The kernel correlation of two arbitrary vectors, x and x’, is the vector $k^{xx'}$ with elements

$$\begin{aligned} k_{i}^{xx'} = \kappa (x', P^{i-1}x) = \varphi ^{T}(x')\varphi (P^{i-1}x) \end{aligned}$$

(7)

Kernel correlation consists of computing the kernel for all relative shifts of two input vectors. This quadratic complexity can be resolved efficiently by diagonalization with DFT.

Depending on the kernel value being unchanged by unitary transformations, such as the DFT, we can use fast kernel correlation for such kernels: dot-product and radial basic function.

Firstly, with dot-product, we have

$$\begin{aligned} k_{i}^{xx'} = g(F^{-1}(\hat{x}^{*} \odot \hat{x'} )) \end{aligned}$$

(8)

where $F^{-1}$ is inverse of DFT. In particular, for a polynomial kernel

$$\begin{aligned} k_{i}^{xx'} = (F^{-1}(\hat{x}^{*} \odot \hat{x'} ) + a)^{b} \end{aligned}$$

(9)

Secondly, for radial basic function

$$\begin{aligned} k_{i}^{xx'} = h(\left\| x \right\| ^2 + \left\| x' \right\| ^2 - 2F^{-1}(\hat{x}^{*} \odot \hat{x'} )) \end{aligned}$$

(10)

As a particularly, useful special case, a Gaussian kernel

$$\begin{aligned} k_{i}^{xx'} = exp(-\frac{1}{\sigma ^2}(\left\| x \right\| ^2 + \left\| x' \right\| ^2 - 2F^{-1}(\hat{x}^{*} \odot \hat{x'} ))) \end{aligned}$$

(11)

[6] proposed simple Matlab code, with a Gaussian kernel, that can run very fast.

3 Kalman Filter

By assuming the system noise has Gaussian distribution, Kalman filter utilizes the linear dynamical systems to resolve the linear optimal filtering problem. More specifically, $x_{n}$ is a discrete time system with state at time n. In the next time step $n+1$, the state is

$$\begin{aligned} x_{n+1} = F_{n+1,n}x_{n} + w_{n+1} \end{aligned}$$

(12)

where $F_{n+1,n}$ is the transition matrix from state $x_n$ to $x_{n+1}$, and $w_{n+1}$ is white Gaussian noise with zero mean and covariance matrix $Q_{n+1}$.

While the measurement vector $z_{n+1}$ is given by

$$\begin{aligned} z_{n+1} = H_{n+1}x_{n+1} + v_{n+1} \end{aligned}$$

(13)

where $H_{n+1}$ is the measurement matrix and $v_{n+1}$ is white Gaussian noise with zero mean and covariance matrix $R_{n+1}$, that is independent of noise $w_{n+1}$. The system gets measurement value for each step then estimates the correct state based on the minimum mean-square error of Eq. (13). The solution is a recursive procedure [2, 8] as illustrated in Algorithm 1.

4 The Proposed Method

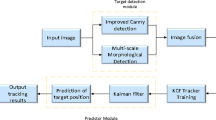
We propose a new tracker that improves the KCF tracker by correcting target’s position with Kalman filter. It is known that KCF often makes failed prediction for the case of occlusion and human crossing simply because the object is disappear. Moreover, performance of the KCF tracker is often deteriorated for rotation, illumination variation, motion blur and etc. We thought that Kalman filter can improve these limitations. In fact, after the KCF estimates target’s position based on the prediction by the Kalman filter, and the estimated value is given to the updating step of the Kalman filter. During the KCF learning phase, our tracker uses the correct state to update the kernel model.

First, the fast detection would acquire the peak value $f_{max}(k)$ at (x(k), y(k)) according to formula [6] in the current frame. Then, Kalman filter uses this position to adjust the system state to correct the position by using Algorithm 1. After several frames of progress, when Kalman filter is stable, it can correct the position of the target in the current frame. Then, during the KCF’s learning phase, it is able to extract the target’s feature successfully for the forthcoming frames.

Secondly, in order to resolve the occlusion as well as human crossing cases, we propose a novel approach. When the peak value is less than threshold T, it is assumed that this is the occlusion case. In other words, KCF would predict the incorrect position in that frame, and we could not use it as a measurement value of Kalman filter. During such case, our tracker will use the target’s position based on the prediction step by Algorithm 1, and only this step will run. Figure 1 and Algorithm 2 describe it in detail.

Fig. 1.

Flowchart of our tracker, which basically combines KCF and Kalman filter.

5 Experiments

5.1 Implementation Details

The present tracker is implemented using Matlab library. The pipeline for the tracker is illustrated in Algorithm 2. Some heuristics are used for threshold value T and Kalman filter. For instance, the sampling rate, acceleration magnitude, process noise, and measurement noise are given as 1 frame/s, 0.2, 0.5, and 1.0, respectively. Performance of our tracker is compared against KCF, MIL and MOSSE trackers. All trackers are implemented using Matlab on Windows 7 running on a computer having an i7 CPU with 16 GB RAM.

5.2 Evaluation

Tracking Dataset. To evaluate the performance, we use 38 video sequences, which are taken from the standard tracking benchmark dataset [3, 14]¹. These videos consist of different challenges for tracking such as illumination variation, rotation, scale, motion blur, occlusion, and human crossing. Performance of the present tracker is compared with those of KCF, MOSSE, and MIL tracker, respectively, by implementing all trackers within the same computer.

Results. The precision curve and the frame rate (fps) are evaluated for each tracker [6, 14]. In this metrics, the ratio of successfully tracked frame is assessed by a set of thresholds within the precision plot. By setting the threshold at 20, we compute the average precision and fps as well as the standard deviation as shown in Table 1. The mean precisions of MIL, MOSSE, KCF, KCF on HOG and our tracker are 41.3, 55.3, 67.9, 90.7 and 96.7 %, respectively. Figure 2 shows the performance curves of five trackers by varying the threshold, suggesting that the present tracker is the best among them. Regarding to the speed, the mean fps of the KCF on HOG case is 148 and the present one runs at 138 fps. Both can run in the real-time applications.

Table 1. Average precision and fps of 5 trackers

Fig. 2.

Comparing the trackers’ performance for full datasets.

Table 2. Average precision of 5 trackers with different categories and datasets (%)

To analyze the detail characteristics, the dataset is divided into six categories: illumination variation, rotation, scale, motion blur, occlusion, and human-crossing. The mean precision for each tracker is obtained for each category as shown in Table 2. Figure 3 shows six graphs. As you can see, the present tracker shows great improvement compared with the KCF on HOG tracker, particularly in the categories of the occlusion and human-crossing cases. This result suggests that Kalman filter plays an important role in making a directional decision when the object drifts into occlusion or other object such as human.

Fig. 3.

Comparing the trackers’ performance for sequence attribute.

Further Analysis for the Human Crossing Case. Since the present tracker shows the best performance for the human-crossing case, it would be necessary to analyze a bit further. Figure 4 demonstrates how 3 trackers, i.e. MIL, MOSSE, and KCF, could not track the walking man correctly except the present one. It seems obvious that those trackers could not deal well with occlusion and human-crossing.

Fig. 4.

Comparing the trackers’ performance for the human-crossing case.

6 Conclusions

In this paper, we present a new tracking framework that combines the best features of the Kernelized Correlation filter and Kalman filter. Using the KCF, we acquire an estimation of the target’s location, which is corrected by Kalman filter for adapting object’s position. It is found that our tracker outperforms the state-of-art trackers such as KCF, MOSSE and MIL. It is particularly excellent in the occlusion and human-crossing cases. Given that KCF is one of the fastest trackers so far, our tracker can be used for the real-time applications such as the high-end surveillance.