Keywords

1 Introduction

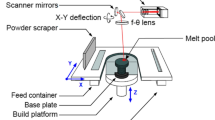
Additive Manufacturing (AM) is a process in which small elements of material are joined to generate parts from 3D model data [1]. Different AM processes exist, which have a layer- or unit wise work principle to create a workpiece [2]. Due to technological advance, the AM process PBF-LB/M is widely used in the industry [3]. In PBF-LB/M a layer of metal powder is spread on a powder bed. The powder bed is then selectively scanned with a laser beam to melt and solidify the metal powder according to a digital plan. Afterwards, another metal powder layer is applied and scanned. This cycle, consisting of applying a powder layer and scanning, is iterated until the workpiece is generated [1, 2].

PBF-LB/M is referred to as a tool-less manufacturing process. No tool-dependent economies of scale and less manufacturability restrictions for the design exist [4, 5]. Because of the advantage of high design freedom, PBF-LB/M is used to manufacture components with lightweight [6], functionally integrated [7], individualized [8], or monolithic design [9]. Due to the absence of tool-dependent economies of scale, PBF-LB/M is used in particular to produce components with small quantities. However, machine investment-dependent economies of scale are present. Low productivity in combination with high machine prices is an obstacle for using the advantages coming from design freedom for series production or to produce components with large volume [4, 5]. To overcome this obstacle machine hourly cost rates must be reduced, productivity increased, or both.

In HIP, high temperature and high pressure are applied to one or more components in a closed process chamber under an argon atmosphere [10]. This leads to deformation of the components. Internal pores and voids are closed, resulting in parts with high density and improved mechanical properties. Due to the higher fatigue properties of densified parts, HIP after PBF-LB/M is used in the aerospace industry [11, 12].

One idea to increase productivity is to additively build a shell geometry with relative density close to 100% that contains a loose powder core to reduce PBF-LB/M manufacturing time in a first step and achieve high density by subsequent HIP [13, 14]. This idea is referred to as shell-core strategy in this work. The shell-core strategy leads to a trade-off between reduced cost for PBF-LB/M and additional cost for HIP. However, to the best authors’ knowledge, an analysis of the cost saving potential of this idea, meaning the cost difference of manufacturing a part with a shell-core strategy compared to direct PBF-LB/M, has not been published. Thus, the aim of this work is to quantify the cost saving potential per part \({csp}_{p}\) of a shell-core strategy for sample parts. This provides information whether investigating the technological challenges of manufacturing shell-core geometries with PBF-LB/M and subsequent HIP, like compensating shrinkage during the HIP process, or mechanical properties, [14] makes sense in further research from an economic perspective.

2 State of the Art in Reducing Costs of PBF-LB/M by Combination with HIP

The idea of combining PBF-LB/M and HIP to increase productivity was published for the first time in [15] and is also addressed in other publications [13, 14, 16].

In [15] manufacturing of cylindrical parts made from Ti-6Al-4V by PBF-LB/M and subsequent HIP for densification are demonstrated. A gas-impermeable shell with at least 92% relative density that encloses an inner geometry with lower relative density is manufactured additively. It is suggested to sinter the internal geometry to a relative density greater than 80% or leave it in the powder state with a relative density of 65% before further densification by HIP [15].

Herzog, Bartsch et al. propose selecting PBF-LB/M process parameters for a high build rate by increasing the scan speed, accepting a low relative density of at least 95% in the as-built state. With a demonstrator build job composed of 3 fuel connectors, made from Ti-6Al-4V on an SLM500L machine, a build time reduction of 24.5% is realized, compared to the parameter set that would achieve relative density close to 100%. In subsequent HIP, 99.8% relative density is achieved [16].

In [14], the idea of manufacturing shrinkage-compensated shell-core geometries with PBF-LB/M is investigated. Different shelled and solid geometries are designed and manufactured using PBF-LB/M, whereas the shelled geometries are densified in subsequent HIP. The shell-core geometries in [14] are not designed for minimizing PBF-LB/M process duration and have thicker shells than possibly needed. Additionally, more support structures than possibly required have been used for bracket sample parts, resulting in reduced time savings. However, the total recorded build time of shelled geometries of 8:48 h is approximately 11% shorter compared to the solid geometries of 9:53 h. Moreover, as an extreme and hypothetical example representing the maximum build time saving potential, the build times of a solid and a shelled block geometry with edge lengths of 240 mm, 240 mm, and 290 mm, are estimated for an EOS M290 machine. The estimated build time of the shelled geometry is 61 h and orders of magnitude shorter, than the build time of the solid block of 836 h [14].

3 Model to Calculate the Cost Saving Potential

In previous publications a combination of PBF-LB/M with HIP to decrease costs is proposed [13,14,15,– 16]. However, \({csp}_{p}\) is not quantified. This research gap is addressed in this work. Therefore, \({csp}_{p}\) of a shell-core strategy is assessed in a case study. In the following section, the process steps and technologies considered in the cost model, the definition of sample parts and PBF-LB/M build jobs, and the cost calculation are described.

3.1 Considered Process Steps and Technologies

It is necessary to consider the process steps where a change of \({csp}_{p}\) is expected due to a shell-core strategy. Because shrinkage during HIP needs to be compensated in a shell-core strategy, less parts fit into one PBF-LB/M build job. That is why fixed costs per job must be allocated to fewer parts and \({csp}_{p}\) is decreased. After PBF-LB/M, parts and the build plate are separated, typically by using a bandsaw or electric discharge machining. After that, the build plate is prepared for another build job by removing remaining supports structures and creating a flat surface by milling. Additionally, the build plate is treated by sandblasting to increase the surface roughness for good connection with the first layer of a build job [17, 18].

The costs for build plate separation (BPS), milling (BPM), and sandblasting (BPB) need to be allocated to the number of parts a job consists of. Because the number of parts per job is determined in PBF-LB/M nesting for those process steps, an increasing effect of BPS, BPM, and BPB on cost per part needs to be considered in the cost calculation model, to not overestimate \({csp}_{p}\).

3.2 Definition of Sample Parts and PBF-LB/M Build Jobs

To calculate \({csp}_{p}\), different sample parts are considered. Therefore, six solid cylindric geometries are defined. For each solid cylindric geometry, one shell-core geometry is derived, that corresponds to the as-print state after PBF-LB/M and before HIP. For each sample part, a PBF-LB/M build job is defined, that consists of multiple nested instances of that part.

Definition of Solid and Corresponding Shell-Core Sample Parts

An overview of the corresponding sample part geometry pairs is given in Table 1, where \(p\) is the identification number of the part, \(g=1\) indicates a solid geometry, and \(g=2\) indicates a shell-core geometry. The radius of the solid geometry with a volume of \({V}_{p,1}\) is expressed by \({r}_{p,1}\) and the height by \({h}_{p,1}\). The outer radius of the shell of the shell-core geometry is \({r}_{p,2,s}\) and the height is \({h}_{p,2,s}\). The volume of the shell, that is fused during PBF-LB/M to achieve the as-built shell-core geometry is \({V}_{p,2,s}\). The wall thickness of the shell is \({w}_{p,2}\). The inner radius of the shell is equal to the radius of the powder core \({r}_{p,2,c}\). The height of the powder core is \({h}_{p,2,c}\).

Table 1. Defined corresponding shell-core and solid geometries
Full size table

\({csp}_{p}\) is expected to depend strongly on the influence of the chosen solid and derived shell-core geometries on the decrease of PBF-LB/M scanning duration, because of a different volume to be fused. Therefore, the following influences on \({csp}_{p}\) regarding the PBF-LB/M scanning duration are considered in the definition of sample geometries:

  • Change of PBF-LB/M part scanning time per part \({\Delta t}_{p, sp}\)

  • Change of PBF-LB/M support scanning time per part \({\Delta t}_{p,ss}\)

  • Change of PBF-LB/M part layer time per part \({\Delta t}_{p,lp}\)

  • Change of PBF-LB/M support layer time per part \({\Delta t}_{p,ls}\)

The difference of volume to be fused of corresponding solid and shell-core geometries is assumed to decrease with higher ratio of surface area to volume of the solid geometry \({SVR}_{p,1}\) for a given \({w}_{p,2}\). Therefore, a negative correlation of \({SVR}_{p,1}\) and \({\Delta t}_{p, sp}\) and in consequence \({SVR}_{p,1}\) and \({csp}_{p}\) is expected. Furthermore, \({SVR}_{p,1}\) has an influence on PBF-LB/M scanning duration. For high \({SVR}_{p,1}\), more slower contour vectors compared to faster hatch vectors and scanning delays occur, resulting in a lower build rate [19]. Thus, sample parts with a \({SVR}_{p,1}\) range of 0.1200–0.3238 are considered in this case study. A value of 2 mm is defined for \({w}_{p,2}\) to achieve a gas tight shell [20].

It is assumed that support structures are built solid, not as a shell-core geometry, and removed before HIP. Shell-core geometries are expected to have a larger area that needs to be supported due to consideration of shrinkage compensation during HIP in the design. Therefore, shell-core geometries require more support structure volume. This leads to an increase of \({\Delta t}_{p, ss}\) for a given support scanning build rate. To account for this influence in this case study, the geometries are oriented in the build space, so the differently sized circular surface areas of the cylindric geometries are parallel to the build plate. Support structures with height of 3 mm are generated using Autodesk Netfabb that connect the downward facing circular surface with the build plate.

Furthermore, the z-height \({hz}_{p,2}\) of shell-core geometries is higher, than of corresponding solid geometries \({hz}_{p,1}\) with equal orientation in the build space and support height, because shrinkage during HIP must be considered in the design.

Because the support height is set to 3 mm for both solid and shell-core geometries, there is no change of \({\Delta t}_{p,ls}\) due to a change of support z-height. However, \({\Delta t}_{p, ls}\) and \({\Delta t}_{p, lp}\) depend the quantity of parts per job. If the build job consists of less parts if a shell-core strategy is applied, layer dependent time per job is distributed to less parts. This leads to an increase of \({\Delta t}_{p, ls}\) and \({\Delta t}_{p, lp}\) and in consequence higher cost per part.

Corresponding solid and shell-core geometries must have the same mass. Otherwise, densification of a shell-core geometry to the corresponding solid geometry during HIP with equal volume would not be possible. Therefore, \({V}_{p,1}\) must be equal to the sum of \({V}_{p,2,s}\) and \({V}_{p,2,c}\) multiplied with the relative density of the powder core \(d\), as expressed in Eq. (1). According to [21], the relative apparent density of IN718 powder is 54.8%. Therefore, 54.8% is assumed for \(d\).

$${V}_{p,1}={V}_{p,2,s}+{V}_{p,2,c}*d$$
(1)
$${h}_{p,2,s} ={h}_{p,1} +2{x}_{p}$$
(2)
$${r}_{p,2,s}={r}_{p,1}+{x}_{p}$$
(3)
$${h}_{p,2,c}={h}_{p,1}+2{x}_{p}-2{w}_{p,2}$$
(4)
$${r}_{p,2,c}={r}_{p,1}+{x}_{p}-{w}_{p,2}$$
(5)

Shrinkage of cylindric shell-core geometry during HIP is not expected to result in an exactly cylindric solid shape, analog to experiments performed with shell-core geometries in [20]. However, it is assumed that the PBF-LB/M build time difference of a solid cylindric geometry and the exact geometry that would result after HIP is neglectable. Therefore, with isostatic pressure during HIP, meaning equally distributed force per outer surface area of the shell geometry, movement of the walls with an equal shrinking distance of \({x}_{p}\) towards the part center with the result of an exact cylinder geometry is assumed. To derive a shell-geometry in the as-built state according to Eqs. (2)–(5), the value of \({x}_{p}\) is required. \({x}_{p}\) is calculated based on the solid geometries, for a given relative density of the powder core.

For the calculation of \({x}_{p}\), Eq. (6) is transformed to Eq. (8). Equations (2)–(5) are used to supplement unknown variables with known variables of Eq. (7). This leads to Eq. (8), where \({x}_{p}\) is the only unknown variable with a given solid geometry of a cylindric part. Thus, Eq. (8) is parametrized for each solid geometry and solved for \({x}_{p}\).

$${{r}_{p,1}}^{2}*{h}_{p,1}={{r}_{p,2,s}}^{2}*{h}_{p,2,s}-{{r}_{p,2,c}}^{2}* {h}_{p,2,c}+{{r}_{p,2,c}}^{2}* {h}_{p,2,c}*d$$
(6)
$${{r}_{p,1}}^{2}*{h}_{p,1}={{r}_{p,2,s}}^{2}*{h}_{p,2,s}+\left(d-1\right)*{{r}_{p,2,c}}^{2}* {h}_{p,2,c}$$
(7)
$$ r_{p,1}^2 *h_{p,1} = (r_{p,1} + x_p )^2 *(h_{p,1} + 2x_p ) + (d - 1)*(r_{p,1} + x_p - w_{p,2} )^2 *(h_{p,1} + 2x_p - 2w_{p,2} ) $$
(8)

Definition of PBF-L/M Build Jobs

In Table 2, the characteristics of the defined build jobs are shown. Less shell-core parts fit into one build job compared to corresponding solid parts due to shrinkage compensation. Thus, an influence on PBF-LB/M as well as BPS, BPM, and BPB \({csp}_{p}\) of due to the quantity of parts per job \({q}_{p,g,ps}\) is expected. The volume per job the outer hull of the solid respectively the shell geometry is indicated by \({V}_{job,p}\).

Table 2. Characterization of the defined build jobs
Full size table

The influence of \({q}_{p,g,ps}\) on \({csp}_{p}\) is considered by setting a maximum nesting density. An integer number of equal instances of each solid respectively shell-core part per build job is calculated for a defined maximum nesting density. Therefore, \({V}_{job,p}\), the EOS M290 build space with an edge length of 250 mm [22] and \({hz}_{p,g}\) are considered. Because this case study is oriented towards a scenario of economical manufacturing of a high production volume, a maximum nesting density of 50% is assumed.

3.3 Cost Calculation

In this section, the equations and required input data for the cost calculation are explained.

Calculation of the Cost Saving Potential

The cost saving potential is calculated per part \({csp}_{p}\), to assess the absolute cost saving potential per part. \({\Delta c}_{p,ps}\) is the change of cost per part \(p\) and process step \(ps\).

$${csp}_{p}=\sum_{ps}{\Delta c}_{p,ps}\,\, where\,\, ps \in \left\{PBF-LB/M, BPS, BPM, BPB, HIP\right\}$$
(9)

Additionally, an assessment of the cost saving potential relative to the part weight and the cost per solid part is used to evaluate the effectiveness of a shell-core strategy in general. Therefore, the cost saving potential relative to the part mass \({csp}_{m,p}\), and relative to the cost for the solid geometry \({csp}_{rel,p}\) is calculated. The mass of a solid geometry is indicated by \({m}_{p,1}\).

$${csp}_{m,p}=\frac{{csp}_{p}}{{m}_{p,1}}$$
(10)
$${csp}_{rel,p}=\frac{{csp}_{p}}{{C}_{p,1}}$$
(11)

\({\Delta c}_{p,ps}\) is calculated based on the cost per part and process step \({C}_{p,g,ps}\) of the shell-core geometry \({C}_{p,2,ps}\) and solid geometry \({C}_{p,1,ps}\).

$${\Delta c}_{p,ps}={C}_{p,1,ps}-{C}_{p,2,ps}$$
(12)

To calculate \({C}_{p,g,ps}\), the cost per job and process step \({C}_{job, p,g,ps}\) is divided by the quantity of parts of that job and process step \({q}_{p,g,ps}\).

$${C}_{p,g,t}=\frac{{C}_{job, p,g,ps}}{{q}_{p,g,ps}}$$
(13)

The equations for calculating \({C}_{job, p,g,ps}\) for all considered process steps are derived from [23,24,25]. \({C}_{job, p,g,ps}\) is the sum of direct materials cost \({C}_{mat}\), direct labor cost \({C}_{l}\), and manufacturing overhead \({C}_{mach}\).

$${C}_{job, p,g,ps}={C}_{mat}+{C}_{l}+{C}_{mach}$$
(14)

To calculate \({C}_{mat}\), the cost rate of a material \({cr}_{mat}\), is multiplied with the required quantity of material per job \({q}_{mat}\).

$${C}_{mat}={cr}_{mat}*{q}_{mat}$$
(15)

According to [26], 95% of the unfused IN718 metal powder can be recovered by recycling for multiple cycles. However, the amount of lost powder is higher, for instance due to shield gas filter residue, aerosol emissions, and cleaning losses [27, 28]. Therefore, the lost amount of powder depends to on the specific use case. To consider powder losses, \({q}_{mat}\) is defined to depend on the material efficiency \({m}_{p,job}\), which is the ratio of all parts in a build job and the part mass to overall used powder \({e}_{mat}\) [28].

$${q}_{mat}=\frac{{m}_{p,job}}{{e}_{mat}}$$
(16)

\({C}_{l}\) is calculated based on the labor cost rate \({cr}_{l}\) and the required duration of labor per job.

$${C}_{l}={cr}_{l}*{d}_{l}$$
(17)

For \({C}_{mach}\) the cost for machine depreciation \({C}_{dep}\), interest \({C}_{i}\), room \({C}_{r}\), electricity \({C}_{el}\), auxiliary materials \({C}_{am}\), and wear parts and maintenance \({C}_{wm}\) per job are considered.

$${C}_{mach}= {C}_{dep}+{C}_{i}+{C}_{r}+{C}_{el}+{C}_{am}+{C}_{wm}$$
(18)

\({C}_{dep}\) is calculated based on the acquisition cost of a machine \({C}_{ac}\), its depreciation period in years \({C}_{ac}\), and the quantity of jobs per year \({q}_{jobs}\).

$${C}_{dep}=\frac{{C}_{ac}}{{p}_{dep}*{q}_{jobs}}$$
(19)

\({q}_{jobs}\) is calculated by dividing the operating hours per year \(oh\) by the duration per job \({d}_{job}.\)

$${q}_{jobs}=\frac{oh}{{d}_{job}}$$
(20)

\({C}_{i}\) is calculated based on the interest rate \(i\), \({C}_{ac}\), \({p}_{dep}\), and \({q}_{jobs}\).

$${C}_{i}=\frac{i*\mathrm{0,5}*{C}_{ac}}{{p}_{dep}*{q}_{jobs}}$$
(21)

\({C}_{r}\) is calculated based on the cost rate per area unit and year \({cr}_{r}\), the quantity of blocked shopfloor area \({q}_{r}\), and \({q}_{jobs}\).

$${C}_{r}=\frac{{cr}_{r}*{q}_{r}}{{q}_{jobs}}$$
(22)

\({C}_{el}\) is the product of the electricity price \({cr}_{e}\), the average power consumption of the machine \({p}_{e}\), and the duration power is consumed \({d}_{e}\).

$${C}_{el}={cr}_{e}*{p}_{e}*{d}_{e}$$
(23)

\({C}_{am}\) is the product of the cost rate for auxiliary material \({cr}_{am}\) and the average required quantity of auxiliary material \({q}_{am}\).

$${C}_{am}={cr}_{am}*{q}_{am}$$
(24)

Input Data

The used input data for the cost calculation is shown in Table 3. The abbreviation pgd. is used to indicate that data depends on the sample part and its’ geometry, that a job consists of. The used assumptions regarding input data of the considered process steps are explained in the following sections.

Table 3. Input data of the cost calculation model
Full size table

Assumptions for PBF-LB/M

The PBF-LB/M machine EOS M290 is selected for the use case in this work because it is an established PBF-LB/M system that is used for industrial production. \({q}_{p,g,PBF-LB/M}\) depends on the specific build job with a defined maximum nesting density of 50%, as explained in 3.2. For \({c}_{mat}\) of IN718, 90€/kg is assumed.

Besides the duration of PBF-LB/M for additive generation, \({d}_{job}\) consists of the time for loading the build job of 34 min, mounting the build plate and coater blade of 19.4 min, calibrating and checking of 10.5 min, heating up and flooding the build chamber with inert gas of 78 min, cooldown of 50 min, and removal of powder and build job of 17.9 min [18]. The duration of additive generation depends on the specific job and is estimated using EOSPrint.

For \({d}_{l}\) of PBF-LB/M, only the manual steps of mounting the build plate and coater blade, calibrating and checking, and removal of powder and build job of are considered. For \({d}_{e}\), heating up and flooding with inert gas and additive generation are considered, because the electricity consumption of the other process elements are assumed to be neglectable.

Because of insolubility of argon in metallic materials, HIP of a shell-core geometry with Argon in the core does not result in a fully dense part [37]. As nitrogen can be used for IN718 in PBF-LB/M [38] and to not introduce Argon in the powder core, nitrogen is assumed as inert gas for PBF-LB/M.

To consider \({C}_{wm}\) of PBF-LB/M, \({C}_{ac}\) is multiplied with 0.1 and divided by \({q}_{jobs}\), following the approach of [24].

Assumptions for BPS, BPM, and BPB

For BPS, BPM, and BPB, \({q}_{p,g,ps}\) is equal to PBF-LB/M. At the beginning of BPS, the build plate and parts are still connected. In BPM and BPB, the build plate is already separated from parts. However, the build plate must be processed by BPM and BPB due to the quantity of part the PBF-LB/M build job consists of.

The duration of BPS, BPM, and BPB consists of the main processing and setup before and afterwards. For the total BPS setup time, a duration of 2 min is assumed. The sawing duration for BPS is calculated by dividing the feed distance by the defined feed rate of the band saw. Based on calculations of the internal software of a Klaeger 3D Cut band saw, a feed rate of 12 mm/min is suitable for IN718 and a width of 250 mm to be cut through, as a conservative assumption for the width of a densely nested PBF-LB/M build job. For milling in BPM, a duration of 60 min and for blasting in BPB of 10 min are assumed for one EOSM290 build plate with IN718, based on information from lab personnel experienced with EOSM290 machines and IN718.

It is assumed for \({d}_{l}\) of BPS and BPB that a person is present during the whole process. For BPM, occupation of personnel is only considered for manual setup operations, because other tasks can be carried out during automated milling.

The value of \(oh\) is set to 2000 h/for BPS, BPB, and BPB, which corresponds to the assumption of two-shift operation on 250 d/a, with the machines being productive for 50% of the time personnel is available.

Moreover, it is assumed, that \({q}_{r}\) equals three times the occupied area by the machine of 4.305 m2 for BPS [34], 3.148 for BPM [35], and 1.15 [36] for BPB, to account for additional space for intralogistics and operators. To consider \({C}_{wm}\) BPS, BPM, and BPB, \({C}_{dep}\) is multiplied with 0.1, following the approach of [18].

Assumptions for HIP

In recent scientific sources, not all required input data for HIP could be found. However, relevant data is available from a whitepaper [25] by the Swedish HIP machine supplier Quintus Technologies. In [25] a calculation of operational costs for processing of additively manufactured turbine blades from IN718 is presented, where the two HIP machines QIH48 and QIH15L with different size and productivity are considered. For the case study in this work, IN718 and the more productive HIP machine QIH48 are chosen, because of the motivation of efficient AM of high quantities or parts with high volume. The acquisition cost of the HIP machines, the machine depreciation period, and the blocked shopfloor area are not provided [25].

On request, different HIP machine suppliers stated to only disclose HIP machine prices in confidential quotes to potential customers. To still achieve the aim of this work, a best-case and worst-case scenario are considered for \({C}_{ac}\) for HIP. According, to [39], published in the year 1985, the price for a mid-size HIP machine with a process chamber width of 0.6 m and height of 1.5 m has been 3 million German mark. In [18], acquisition cost of 1 million € is assumed for one HIP machine, but no information regarding the HIP machine model is provided. A span of 1 million € for a best-case to 5 million € for a worst-case scenario for \({C}_{ac}\) are considered in this work.

For HIP, \({q}_{p,g,HIP}\) is calculated by dividing the maximum payload per job of 175 kg of a QIH48 machine [25] by the part mass. Moreover, it is assumed, that \({q}_{r}\) equals three times the blocked area by the machine dimensions of 31.5 m2 [30], to account for additional space for intralogistics and operators.

4 Assessment of the Cost Saving Potential of a Shell-Core Strategy

In this section, the cost saving potential per part, per part mass, and relative to the cost per part without shell-core strategy are assessed. Moreover, the change of cost per process step and the change of duration of additive generation in PBF-LB/M are assessed.

4.1 Cost Saving Potential Per Part

As explained in Sect. 3.2, a negative influence of \({SVR}_{p,1}\) on \({csp}_{p}\), is expected. \({SVR}_{p,1}\) is known for solid parts, without definition of corresponding shell-core geometries. Thus, \({SVR}_{p,1}\) is suitable as indicator to assess \({csp}_{p}\) without knowledge and effort to derive of the exact corresponding shell geometry.

Fig. 1.
figure 1

Cost saving potential per part

Full size image

In Fig. 1 \({csp}_{p}\) and in Fig. 2, \({csp}_{m,p}\), and \({csp}_{rel,p}\) are depicted depending on \({SVR}_{p,1}\). For all considered sample parts, \({csp}_{p}\) is positive. This indicates that a shell-core strategy has the potential to achieve lower cost compared to direct PBF-LB/M with the assumptions made in this case study.

Fig. 2.
figure 2

Cost saving potential per part mass (left) and cost saving potential relative to the cost per part without shell-core strategy (right)

Full size image

Also, \({csp}_{p,m}\) and \({csp}_{p,rel}\) are positive and show negative correlation with \({SVR}_{p,1}\). Thus, especially parts with low \({SVR}_{p,1}\) should be considered for the application of a shell-core strategy to successfully reduce cost.

4.2 Change in Cost Per Part and Process Step

To identify the influence of the considered process steps, \({\Delta c}_{p,ps}\) is assessed. The values are displayed in Table 4. The result indicates that the reduced cost for PBF-LB/M clearly exceeds the increased cost due to less parts per job in BPS, BPM, and BPB and the additional process step HIP with a shell-core strategy, especially for low \({SVR}_{p,1}\). This is the case for both the best- and worst-case scenario. The process step with the highest cost increasing effect is HIP, whereas the influence of BPS, BPM, and BPB is only minor.

Table 4. Change in cost per process step per sample part due to a shell-core strategy
Full size table

4.3 Change of Duration of Additive Generation in PBF-LB/M

The assessment in Sect. 4.2 indicates that a decreased PBF-LB/M build time is crucial to achieve positive \({csp}_{p}\) with a shell-core strategy. Thus, the change of duration for additive generation per part \({\Delta t}_{p}\), which consists of scanning and application of new powder layers, and its components \({\Delta t}_{s,sp}\), \({\Delta t}_{s,ss}\), \({\Delta t}_{s,pl}\) and \({\Delta t}_{s,sl}\) are evaluated. The change of duration for additive generation of PBF-LB/M per part due to a shell-core strategy is shown in Table 5.

Table 5. Change of duration for scanning and application of new layers of PBF-LB/M per part due to a shell-core strategy
Full size table

For all considered sample parts, the value of \({\Delta t}_{p}\) is positive, because the increasing effect of \({\Delta t}_{p,sp}\) is bigger than the decreasing influence of \({\Delta t}_{p,ss}\), \({\Delta t}_{p,lp}\) and \({\Delta t}_{p,ls}\). These results indicate, that due to a shorter PBF-LB/M build time, machine cost for additive generation during PBF-LB/M can be decreased by a shell-core strategy for the chosen sample parts.

5 Conclusion

In this work, the cost saving potential of a shell-core strategy was assessed. The shell-core strategy is characterized by a hybrid manufacturing process, where a shelled geometry with loose powder core is generated using PBF-LB/M and densified to a relative density close to 100% by subsequent HIP. This leads to a higher productivity and thus less cost per part for PBF-LB/M, but higher costs for BPS, BPM, BPB, and the additional process step HIP. Depending on the geometry of a part, the shell-core strategy can result in a cost reduction compared do direct manufacturing of a solid part geometry with PBF-LB/M. The results indicate a high cost saving potential for parts with a low surface area to volume ratio.

A limitation of the presented work is missing data for the acquisition cost of a HIP machine. However, a positive cost saving potential is possible, even for parts with high surface area to volume ration in the worst-case scenario with assumption of HIP acquisition of 5,000,000 €. Furthermore, the influence of the wall thickness of the shell-geometry was not investigated in this work.

Thus, future research should assess the influence of the wall thickness on the cost saving potential. Moreover, future research should investigate the estimation of cost saving potential with low effort based on the surface area to volume ratio in consideration of the wall thickness for real world applications including all post-processing steps. This should be combined with research of methods to determine shell-core geometries for parts with complex target geometry. Furthermore, possible anisotropic shrinkage behavior of parts during HIP due to their orientation in PBF-LB/M should be considered.