Abstract
Trace properties, which are sets of execution traces, are often used to analyze systems, but their expressiveness is limited. Clarkson and Schneider defined hyperproperties as a generalization of trace properties to sets of sets of traces. Typical applications of hyperproperties are found in information flow security. We introduce an analogous definition of concurrent hyperproperties, by generalizing traces to concurrent traces, which we define as partially ordered multisets. We take Petri nets as the basic semantic model. Concurrent traces are formalized via causal nets. To check concurrent hyperproperties, we define may and must testing of sets of concurrent traces in the style of DeNicola and Hennessy, using the parallel composition of Petri nets. In our approach, we thus distinguish nondeterministic and concurrent behavior. We discuss examples where concurrent hyperproperties are needed.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Among the most fundamental debates in the theory of concurrency is the distinction between interleaving semantics in the style of Milner [17] and Hoare [13], and partial-order (or true concurrency) semantics following the work of Petri [21], Mazurkiewicz [15], and Winskel [27]. In interleaving semantics, concurrency is reduced to its sequential nondeterministic simulation; in partial-order semantics, concurrency is modeled as causal independence.
In this paper, we revisit this classic debate in the modern setting of hyperproperties. Clarkson and Schneider defined hyperproperties as a generalization of trace properties, which are sets of traces, to sets of sets of traces [4]. Hyperproperties are a powerful class of linear-time properties that can express many notions related to information flow, symmetry, robustness, and causality. A typical example is noninterference [8], which is one of the most well-studied information-flow security policies. Noninterference requires that for all computations and for all sequences of actions of a high-security agent A, the resulting observations made by a low-security observer B are identical to B’s observations that would result without A’s actions. While trace properties express properties of individual executions, hyperproperties express properties of sets of traces. This makes it possible to relate different executions, for example by requiring that certain observations are the same, without necessarily restricting the events on individual executions.
Since hyperproperties refer to traces, they are, at least in principle, immediately applicable to concurrent systems with interleaving semantics. However, the interleaving semantics leads to a fundamental problem, which we will illustrate with a sequence of example systems given as the Petri nets shown in Fig. 1. We employ the usual graphical representation of Petri nets: circles represent places and boxes represent transitions that are connected to places via directed arcs. In our setting, transitions are labeled by action symbols like \(h_1\) and \(h_2\). Black dots represent tokens, which represent the current points of activity. The simultaneous presence of several tokens models concurrent activities. The dynamic behavior of a Petri net is modeled by its token game that defines how tokens can move inside the net. A transition is enabled if all places connected to it with an ingoing arc carry a token. Firing the transition moves these tokens to the places connected to it with an outgoing arc. Branching from a place models nondeterministic choice, whereas branching from a transition models the start of a concurrent execution. As an example, consider the net \(\mathcal N_C\) shown on the right in Fig. 1. From the initial place \(p_0\), there is a nondeterministic choice between the transitions labeled with \(h_1\) and \(h_2\). Firing transition \(h_1\) concurrently enables the transitions labeled with \(l_1\) and \(l_2\), whereas firing transition \(h_2\) enables in place \(p_{13}\) the nondeterministic choice between the transitions \(l_1\) and \(l_2\). For more details on Petri nets we refer to Sect. 3.
Left: The three maximal runs \(\rho _1, \rho _2\) and \(\rho _3\) of \(\mathcal N_C\) from Fig. 1, resulting by resolving every nondeterministic choice in \(\mathcal N_C\), and their corresponding concurrent traces \(\pi _1, \pi _2\) and \(\pi _3\). Right: A sequential test \({\mathcal {T}_{{{ seq }}}}\) for the concurrent hyperproperty that every pair of concurrent traces \(\pi \) and \(\pi '\) must agree on the occurrence and sequential ordering of the low-security events \(l_1\) and \(l_2\). In the test, the events \(l_1\) and \(l_2\) refer to \(\pi \) and \(l'_1\) and \(l'_2\) to \(\pi '\). The place marked with the symbol  notifies a successful test. Below is a concurrent test \({\mathcal {T}_{{{ con }}}}\) for the weaker concurrent hyperproperty that every pair of concurrent traces \(\pi \) and \(\pi '\) must agree on the occurrence of the low-security events \(l_1\) and \(l_2\), but not on their sequential ordering. For instance, each each \(l_1\) must be matched by \(l'_1\) before the next \(l_1\) can occur, but \(l_2\) may occur in between \(l_1\) and \(l'_1\).
notifies a successful test. Below is a concurrent test \({\mathcal {T}_{{{ con }}}}\) for the weaker concurrent hyperproperty that every pair of concurrent traces \(\pi \) and \(\pi '\) must agree on the occurrence of the low-security events \(l_1\) and \(l_2\), but not on their sequential ordering. For instance, each each \(l_1\) must be matched by \(l'_1\) before the next \(l_1\) can occur, but \(l_2\) may occur in between \(l_1\) and \(l'_1\).
For a start, consider the system \(\mathcal N_A\) shown on the left in Fig. 1. We are interested in the secrecy property that the system’s low-security behavior, as observable in the low-security events \(l_1\) and \(l_2\), is not affected by the high-security events \(h_1\) and \(h_2\). Our system is secure. This is captured by the hyperproperty that all traces must agree on the occurrences and the ordering of \(l_1\) and \(l_2\), and indeed, the system has only two traces, \(h_1 \cdot l_1 \cdot l_2\) and \(h_2 \cdot l_1 \cdot l_2\), which, when projected to \(\{l_1, l_2\}\), both result in the same sequence \(l_1 \cdot l_2\) of low-security events.
Next, consider system \(\mathcal N_B\) shown in the middle in Fig. 1. Informally, the system is still secure in the sense that an observer who sees only \(l_1\) and \(l_2\) cannot distinguish the situation where \(h_1\) has occurred from the situation where \(h_2\) has occurred. However, our previous hyperproperty is violated. The system has four traces: \(h_1 \cdot l_1\), \(h_1 \cdot l_2\), \(h_2\cdot l_1\), and \(h_2\cdot l_2\), which, when projected to \(\{l_1, l_2\}\), result in two different traces, \(l_1\) and \(l_2\). This issue is due to the nondeterministic choice between \(l_1\) and \(l_2\), and can be addressed with possibilistic information-flow properties like generalized noninterference [16]. Generalized noninterference is weaker than normal noninterference: it requires that for every pair of traces \(\pi , \pi '\) there exists another trace \(\pi ''\), such that (1) \(\pi ''\) agrees with \(\pi \) on the low-security events \(\{l_1, l_2\}\) and (2) \(\pi ''\) agrees with \(\pi '\) on the high-security events \(\{h_1, h_2\}\). Generalized noninterference is satisfied in \(\mathcal N_B\). For example, for \(\pi =h_1 \cdot l_1\) and \(\pi '=h_2\cdot l_2\), there exists \(\pi ''= h_2\cdot l_1\), which agrees with \(\pi \) on \(\{l_1, l_2\}\) and with \(\pi '\) on \(\{h_1, h_2\}\).
Finally, consider the concurrent system \(\mathcal N_C\) shown on the right in Fig. 1. With the interpretation of concurrency as nondeterministic interleaving, the system has the four traces \(h_1\cdot l_1 \cdot l_2\), \(h_1\cdot l_2 \cdot l_1\), \(h_2\cdot l_1 \cdot l_2\), and \(h_2\cdot l_2 \cdot l_1\). Generalized noninterference is satisfied. However, the system is clearly not secure, because \(h_1\) causes concurrent behavior, while \(h_2\) causes sequential behavior. In a concurrent setting, this difference could be recognized by an attacker, who might, for example, synchronize with the system on a particular ordering, such as \(l_1 \cdot l_2\). In a trace that begins with \(h_1\), this will always work, while in traces that begin with \(h_2\), the attacker might observe a deadlock when the system performs the order \(l_2 \cdot l_1\).
In the security literature, this phenomenon has lead to the study of branching-time information-flow properties based on various notions of (bi-)simulation (cf. [3]). Often, however, such equivalences are too fine-grained, because they expose the point in time when an internal decision is made. Linear-time properties, and, hence, hyperproperties abstract from such implementation details. Can hyperproperties nevertheless recognize the difference between concurrent and sequential behavior?
In this paper, we propose concurrent hyperproperties as a positive answer to this question. Hyperproperties are based on the partial-order interpretation of concurrency. We stick to Clarkson and Schneider’s definition of hyperproperties as sets of sets of traces, but generalize traces to concurrent traces, which we define as partially ordered multisets (pomsets). Figure 2 shows the three maximal runs \(\rho _1, \rho _2\) and \(\rho _3\) of system \(\mathcal N_C\) and their corresponding concurrent traces. In a run, every nondeterministic choice has been resolved, but concurrent executions remain visible, like the concurrency of the transitions labeled with \(l_1\) and \(l_2\) in \(\rho _1\). The concurrency of run \(\rho _1\) is reflected in the partial order of the concurrent trace \(\pi _1\). Note that \(\mathcal N_C\) has four traces under the interleaving semantics (corresponding to the two nondeterministic choices and the two possible interleavings) but only three concurrent traces, because the concurrent execution is not resolved by nondeterminism. Since the concurrency is still present in the concurrent traces, a concurrent hyperproperty can distinguish nondeterminism from concurrency. Continuing our example, we can now specify secrecy in concurrent systems like \(\mathcal N_C\) as the concurrent hyperproperty where every pair of concurrent traces agrees on the occurrence and ordering of the low-security events. Our example system clearly violates this requirement.
In the paper, we give a formal definition of concurrent hyperproperties and then provide an explicit mechanism for describing concurrent hyperproperties. We base this mechanism the concept of testing processes due to DeNicola and Hennessy [5, 11]. There the interaction of a (nondeterministic) process and a user is explicitly formalized using a synchronous parallel composition. The user is formalized by a test, which is a process with some states marked as a success. It is defined when a process may pass a test and when it must pass a test. We transfer the concept of testing to concurrent traces. A concurrent hyperproperty is given as a test that has interactions with multiple concurrent runs. The test is successful for a given set of concurrent traces if it succeeds for all combinations of concurrent traces from the set.
For our example, such a test \({\mathcal {T}_{{{ seq }}}}\) is shown on the right in Fig. 2. It can interact with any two of the runs \(\rho _1, \rho _2, \rho _3\) corresponding to any two of the traces \(\pi _1, \pi _2, \pi _3\) of \({\mathcal {N}_{{{C}}}}\). The interaction is via parallel composition that synchronizes on all transitions with the same label. To this end, the first run under test keeps the original labels \(l_1\) and \(l_2\), whereas the second run uses primed copies \(l_1'\) and \(l_2'\) of these labels. Thus \({\mathcal {T}_{{{ seq }}}}\) allows for both possible orderings (\(l_1\) then \(l_2\), and \(l_2\) then \(l_1\)) in the first trace and enforces that the second trace exhibits the same order. When \({\mathcal {T}_{{{ seq }}}}\) is applied to the runs of the concurrent system \({\mathcal {N}_{{{C}}}}\) shown on the left of Fig. 2, it turns out that they may not pass this test, for instance, when \(\rho _1\) and \(\rho _3'\), i.e., \(\rho _3\) with primed labels, are tested for the sequence \(l_1 \cdot l_1' \cdot l_2 \cdot l_2'\), this leads to a deadlock after \(l_1\). This shows that the concurrent system \({\mathcal {N}_{{{C}}}}\) does not satisfy the concurrent hyperproperty. We will examine this in more detail in Sect. 5.
The test \({\mathcal {T}_{{{ con }}}}\) checks a weaker concurrent hyperproperty, namely that each occurrence of \(l_1\) is matched by an occurrence of \(l'_1\) before the next occurrence of \(l_1\), and similarly for \(l_2\) and \(l'_2\), but \(l_2\) may occur in between \(l_1\) and \(l'_1\). When \({\mathcal {T}_{{{ con }}}}\) is applied to any two of the runs \(\rho _1, \rho _2, \rho _3\) shown on the left of Fig. 2, it turns out that they must pass this test. This shows that the concurrent system \({\mathcal {N}_{{{C}}}}\) satisfies this weaker concurrent hyperproperty. For more details see Sect. 5.
Our paper is organized as follows. In Sect. 2 we define the notion of concurrent hyperproperties and give examples of ascending sophistication. In Sect. 3 we recall the basic concepts from Petri nets that we take as our semantic model of concurrent systems. In particular, we define concurrent runs and the parallel composition of nets. In Sect. 4 we adapt the concept of testing developed by DeNicola and Hennessy to the setting of Petri nets. In Sect. 5 we discuss how various examples of concurrent hyperproperties can be tested. In Sect. 6 we briefly discuss the decidability of universal must testing and establish an undecidability result for universal may testing. In Sect. 7 we conclude the paper.
Dedication. We dedicate our paper to Jifeng He on the occasion of his 80th birthday. Jifeng has made many contributions to formalizing and relating different semantic models of computing, as exemplified in his book ‘Unifying Theories of Programming’ with Tony Hoare [12]. Out of this work grew also Jifeng’s interest in testing [1, 25, 26], the concept that we employ for hyperproperties in this paper, although in an abstract setting of testing processes as introduced by DeNicola and Hennessy. The second author has very pleasant memories of the close cooperation with Jifeng within the EU Basic Research Action ProCoS (Provably Correct Systems) during the period 1989–1995 [10], and of various scientific meetings, in particular in Oxford, Oldenburg, and Shanghai.
2 Concurrent Hyperproperties
Clarkson and Schneider defined hyperproperties as a generalization of trace properties, which are sets of traces, to sets of sets of traces [4]. To give an analogous definition of concurrent hyperproperties, we generalize traces to concurrent traces, which we define as partially ordered multisets (pomsets).
Let \(\varSigma \) be a set of labels. A \(\varSigma \)-labeled partially ordered set is a triple \((X, <, \ell )\) where < is an irreflexive partial order on a set X and \(\ell : X \rightarrow \varSigma \) is a labeling function. Two such sets \((X,<,\ell )\) and \((X', <', \ell ')\) are isomorphic if there exists a bijective mapping \(f: X \rightarrow X'\) such that \(f(x)< f(y) \Leftrightarrow x<y\) and \(\ell '(f(x)) = \ell (x)\). A partially ordered multiset (pomset) over \(\varSigma \) is an isomorphy class of \(\varSigma \)-labeled partial ordered sets, denoted as \([(X, <, \ell )]\). A totally ordered multiset (tomset) is a pomset where < is a total order [23].
We then refer to tomsets over \(\varSigma \) as traces and pomsets over \(\varSigma \) as concurrent traces. A trace property is a set of traces; a hyperproperty is a set of sets of traces. Analogously, a concurrent trace property is a set of concurrent traces, and a set of sets of concurrent traces is a concurrent hyperproperty. We denote with \(\mathbb {T}(\varSigma )\) the set of all concurrent traces over \(\varSigma \).
Example 1
A simple information flow policy for a concurrent system is to forbid any dependency of a low-security event labeled l (for low) on a high-security event labeled h (for high). Let \(\varSigma =\{ l, h \}\). The policy can be expressed as the concurrent trace property
Example 2
Consider the hyperproperty that every pair of concurrent traces agrees on the occurrence of the low-security events, independent on any other event. Let \(\varSigma _{ low }\) be the set of low-security events. The requirement can then be formalized as the following concurrent hyperproperty \(H_1\):
where \(X_{ low } = \{ x \in X \mid \ell (x) \in \varSigma _{ low }\}\) and \(X'_{ low } = \{ x \in X' \mid \ell '(x) \in \varSigma _{ low }\}\).
In the introduction, we discussed the concurrent hyperproperty that every pair of concurrent traces agrees both on the occurrence and the ordering of the low-security events. This requirement can be formalized as the following concurrent hyperproperty \(H_2\):
Example 3
As a final example, we adapt the notion of generalized noninterference (GNI) [16] to concurrent traces. We identify the events as low-security and high-security: \(\varSigma = \varSigma _{ low } \cup \varSigma _{ high }\). The policy then requires that for every pair of concurrent traces there exists a third concurrent trace that agrees with the first trace on the low-security events and with the second trace on the high-security events. Unlike the trace-based version discussed in the introduction, this version of GNI distinguishes nondeterminism from concurrency; in the example system \(\mathcal N_C\) shown on the right in Fig. 1, GNI on traces is satisfied, but GNI on concurrent traces is violated. GNI on concurrent traces is expressed by the following concurrent hyperproperty \(H_3\):
where
3 Petri Nets
As a model for concurrent systems we take Petri nets because they distinguish the fundamental concepts of causal dependency, nondeterministic choice, and concurrency explicitly. We consider here safe Petri nets [24], with the transitions labeled by actions which serve as synchronization points in a parallel composition of such nets. We use the notation from [19], which is inspired by [9]. A Petri net or simply net is a structure  , where
, where
-
1.
\({{A}_{{{}}}}\) is a finite communication alphabet with \(\tau \not \in A\),
-
2.
\({{Pl}_{{{}}}}\) is a possibly infinite set of places,
-
3.
 \(\subseteq \) \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) \(\times \) (\({{A}_{{{}}}}\) \(\cup \) { \(\tau \) }) \(\times \) \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) is the transition relation,
\(\subseteq \) \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) \(\times \) (\({{A}_{{{}}}}\) \(\cup \) { \(\tau \) }) \(\times \) \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) is the transition relation, -
4.
\({{M}_{{{0}}}}\) \(\in \) \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) is the initial marking.
We let \({{p}_{{{}}}}\), \({{q}_{{{}}}}\), \({{r}_{{{}}}}\) range over \({{Pl}_{{{}}}}\). The notation \({\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\) stands for the set of all non-empty, finite subsets of \({{Pl}_{{{}}}}\). An element (\({{I}_{{{}}}}\), \({{u}_{{{}}}}\), \({{O}_{{{}}}}\)) \(\in \)  with \({{I}_{{{}}}}, {{O}_{{{}}}} \in {\mathcal {P}_{{{nf}}}}({{Pl}_{{{}}}})\) and \({{u}_{{{}}}} \in {{A}_{{{}}}} \cup \{\tau \}\) is called a transition (labeled with the action \({{u}_{{{}}}}\)) and written as
with \({{I}_{{{}}}}, {{O}_{{{}}}} \in {\mathcal {P}_{{{nf}}}}({{Pl}_{{{}}}})\) and \({{u}_{{{}}}} \in {{A}_{{{}}}} \cup \{\tau \}\) is called a transition (labeled with the action \({{u}_{{{}}}}\)) and written as

For a transition  its preset or input is given by pre(\({{t}_{{{}}}}\)) = \({{I}_{{{}}}}\), its postset or output by post(\({{t}_{{{}}}}\)) = \({{O}_{{{}}}}\), and its action by act(\({{t}_{{{}}}}\)) = \({{u}_{{{}}}}\). The letter \(\tau \) is intended to model an internal action.
its preset or input is given by pre(\({{t}_{{{}}}}\)) = \({{I}_{{{}}}}\), its postset or output by post(\({{t}_{{{}}}}\)) = \({{O}_{{{}}}}\), and its action by act(\({{t}_{{{}}}}\)) = \({{u}_{{{}}}}\). The letter \(\tau \) is intended to model an internal action.
In the graphical representation of a net  we mention the alphabet \({{A}_{{{}}}}\) separately and display the components \({{Pl}_{{{}}}}\),
we mention the alphabet \({{A}_{{{}}}}\) separately and display the components \({{Pl}_{{{}}}}\),  and \({{M}_{{{0}}}}\) as usual. Places \({{p}_{{{}}}}\) \(\in \) \({{Pl}_{{{}}}}\) are represented as circles \(\bigcirc \) with the name \({{p}_{{{}}}}\) outside and transitions
and \({{M}_{{{0}}}}\) as usual. Places \({{p}_{{{}}}}\) \(\in \) \({{Pl}_{{{}}}}\) are represented as circles \(\bigcirc \) with the name \({{p}_{{{}}}}\) outside and transitions

as boxes  carrying the label \({{u}_{{{}}}}\) inside and connected via directed arcs to the places in pre(\({{t}_{{{}}}}\)) and post(\({{t}_{{{}}}}\)):
carrying the label \({{u}_{{{}}}}\) inside and connected via directed arcs to the places in pre(\({{t}_{{{}}}}\)) and post(\({{t}_{{{}}}}\)):

Since pre(\({{t}_{{{}}}}\)) and post(\({{t}_{{{}}}}\)) need not be disjoint, some of the outgoing arcs of  may actually point back to places in pre(\({{t}_{{{}}}}\)) and thus introduce cycles. Graphically, we employ then double-headed arrows between
may actually point back to places in pre(\({{t}_{{{}}}}\)) and thus introduce cycles. Graphically, we employ then double-headed arrows between  and the places in \({ pre}{({{t}_{{{}}}})} \cap { post}{({{t}_{{{}}}})}\). The initial marking \({{M}_{{{0}}}}\) is represented by putting a token \(\bullet \) into the circle of each \({{p}_{{{}}}}\) \(\in \) \({{M}_{{{0}}}}\).
and the places in \({ pre}{({{t}_{{{}}}})} \cap { post}{({{t}_{{{}}}})}\). The initial marking \({{M}_{{{0}}}}\) is represented by putting a token \(\bullet \) into the circle of each \({{p}_{{{}}}}\) \(\in \) \({{M}_{{{0}}}}\).
Starting from the initial marking, the firing of transitions creates new markings \(M \in {\mathcal {P}_{{{ nf }}}} ({{Pl}_{{{}}}})\), which represent the global states of a Petri net. Formally, a transition t is enabled at a marking M if \( pre (t) \subseteq M\). Firing such a transition t at M yields the successor marking \(M' = (M - pre (t)) \cup post (t)\). We write then \(M [t\rangle M'\). We assume here that \(\cup \) is a disjoint union, which is satisfied if the net is contact-free, i.e., if for all \(t \in \mathcal {T}\) and all reachable markings M
The set of reachable markings of a net \(\mathcal N\) is defined by
For \(n=0\) inside this set, it is understood that \(M_0 = M\) holds, so \(M_0 \in { reach}(\mathcal {N})\). In the present setting, all reachable markings are non-empty, finite sets of places. Such Petri nets are called safe or 1-bounded because every reachable marking contains at most one token per place. In general place/transition nets, the reachable markings can be multisets representing multiple tokens per place.
3.1 Causal Nets and Runs
Concurrent computations of a net can be described by causal nets [21, 24]. Informally, a causal net is an acyclic net where all choices have been resolved. It can be seen as a net-theoretic way of defining a partial order among the occurrences of transitions in a net to represent their causal dependency.
We need more notation for a net  . For a place \({{p}_{{{}}}}\) \(\in \) \({{Pl}_{{{}}}}\) its preset is defined by
. For a place \({{p}_{{{}}}}\) \(\in \) \({{Pl}_{{{}}}}\) its preset is defined by  and its postset by
and its postset by  . The flow relation \({{\mathcal {F}}_{{{\mathcal {N}_{{{}}}}}}}\) \(\subseteq \) \({{Pl}_{{{}}}}\) \(\times \) \({{Pl}_{{{}}}}\) on the places of \({\mathcal {N}_{{{}}}}\) is given by
. The flow relation \({{\mathcal {F}}_{{{\mathcal {N}_{{{}}}}}}}\) \(\subseteq \) \({{Pl}_{{{}}}}\) \(\times \) \({{Pl}_{{{}}}}\) on the places of \({\mathcal {N}_{{{}}}}\) is given by

\({{\mathcal {F}}_{{{\mathcal {N}_{{{}}}}}}}\) is well-founded if there are no infinite backward chains
A causal net is a net \({\mathcal {N}_{{{\ }}}}\)= ( \({{A}_{{{}}}}\), \({{Pl}_{{{}}}}\),  , \({{M}_{{{0}}}}\)) such that
, \({{M}_{{{0}}}}\)) such that
-
(1)
all places are unbranched, i.e., \(\ \forall {{p}_{{{}}}}\ \in {{Pl}_{{{}}}}\,.\ |{ pre}{({{p}_{{{}}}})}| \le 1 ~\text {and}~ |{ post}{({{p}_{{{}}}})}| \le 1,\)
-
(2)
the flow relation \({{\mathcal {F}}_{{{\mathcal {N}_{{{}}}}}}}\) is well-founded, and
-
(3)
the initial marking consists of all places without an ingoing arc, i.e.,
$$ {{M}_{{{0}}}}\ = \{{{p}_{{{}}}}\ \in {{Pl}_{{{}}}}\ |\ { pre}{({{p}_{{{}}}})}\ = \emptyset \}. $$
By condition (1), there are no choices in \({\mathcal {N}_{{{}}}}\). Condition (2) implies that the transitive closure of \({{\mathcal {F}}_{{{\mathcal {N}_{{{}}}}}}}\) is irreflexive. Thus a causal net \({\mathcal {N}_{{{\ }}}}\)is acyclic, so each transition occurs only once. Conditions (1)–(3) ensure that there are no superfluous places and transitions in causal nets: every transition can fire and every place is contained in some reachable marking. Also, every causal net is safe.
Following Petri’s intuition, causal nets should describe the concurrent computations of a net. Thus we explain how causal nets relate to ordinary (safe) nets. To this end, we use the following notion of embedding.
Let  be a causal net and
be a causal net and  be a safe net, where \({{M}_{{{01}}}}\) and \({{M}_{{{02}}}}\) denote the initial markings of \({\mathcal {N}_{{{1}}}}\) and \({\mathcal {N}_{{{2}}}}\), respectively. \({\mathcal {N}_{{{1}}}}\) is a causal net of \({\mathcal {N}_{{{2}}}}\) if \({{A}_{{{1}}}}\) = \({{A}_{{{2}}}}\) and there exists a mapping
be a safe net, where \({{M}_{{{01}}}}\) and \({{M}_{{{02}}}}\) denote the initial markings of \({\mathcal {N}_{{{1}}}}\) and \({\mathcal {N}_{{{2}}}}\), respectively. \({\mathcal {N}_{{{1}}}}\) is a causal net of \({\mathcal {N}_{{{2}}}}\) if \({{A}_{{{1}}}}\) = \({{A}_{{{2}}}}\) and there exists a mapping  , which is extended elementwise to subsets \(X \subseteq {{Pl}_{{{1}}}}\) by putting \(f(X) = \{ f(p) \in {{Pl}_{{{2}}}} \mid p \in X \}\), such that the following holds:
, which is extended elementwise to subsets \(X \subseteq {{Pl}_{{{1}}}}\) by putting \(f(X) = \{ f(p) \in {{Pl}_{{{2}}}} \mid p \in X \}\), such that the following holds:
-
1.
\({f_{{{}}}}\)(\({{M}_{{{01}}}}\)) = \({{M}_{{{02}}}}\),
-
2.
\(\forall \) \({{M}_{{{}}}}\) \(\in \) reach(\({\mathcal {N}_{{{1}}}}\)). \({f_{{{}}}}\) \(\downarrow \) \({{M}_{{{}}}}\), the restriction of f to \(M \subseteq {{Pl}_{{{1}}}}\), is injective,
-
3.
\(\forall \) \({{t}_{{{}}}}\) \(\in \)
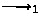 . \( ({f_{{{}}}}({ pre}{({{t}_{{{}}}})}), { act}{({{t}_{{{}}}})}, {f_{{{}}}}({ post}{({{t}_{{{}}}})})) \in \)
. \( ({f_{{{}}}}({ pre}{({{t}_{{{}}}})}), { act}{({{t}_{{{}}}})}, {f_{{{}}}}({ post}{({{t}_{{{}}}})})) \in \) 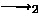 ,
,
The mapping \({f_{{{}}}}\) is called an embedding of \({\mathcal {N}_{{{1}}}}\) into \({\mathcal {N}_{{{2}}}}\). Note that f distributes over the flow relation:
In net theory, the pair \(({\mathcal {N}_{{{1}}}}, {f_{{{}}}})\) is called a process of \({\mathcal {N}_{{{2}}}}\) [2, 21]. We call it a (concurrent) run of \({\mathcal {N}_{{{2}}}}\) and use the (possibly decorated) letter \(\rho \) for runs. A run \(\rho = ({\mathcal {N}_{{{1}}}}, {f_{{{}}}})\) of \({\mathcal {N}_{{{2}}}}\) is called maximal if
so the run \(\rho \) cannot stop at a place p if there is an extension possible at the corresponding place f(p) in \({\mathcal {N}_{{{2}}}}\).
3.2 Causal Nets Corresponding to Concurrent Traces
A causal net \({\mathcal {N}_{{{}}}}\) corresponds to the concurrent trace (pomset) \([(X,<,\ell )]\), where
-
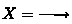 , the set of transitions of \({\mathcal {N}_{{{}}}}\),
, the set of transitions of \({\mathcal {N}_{{{}}}}\), -
< is the transitive closure of the immediate causal successor relation \(<_m\) between transitions: \({{t}_{{{1}}}} <_m {{t}_{{{2}}}}\) holds for
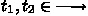 if \(\ { post}{({{t}_{{{1}}}})} \cap { pre}{({{t}_{{{2}}}})} \ne \emptyset \),
if \(\ { post}{({{t}_{{{1}}}})} \cap { pre}{({{t}_{{{2}}}})} \ne \emptyset \), -
\(\ell (t) = { act}{}({{t}_{{{}}}})\) for every
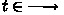 .
.
The irreflexive partial order \({{t}_{{{1}}}} < {{t}_{{{2}}}}\) expresses that transition \({{t}_{{{2}}}}\) can occur only after transition \({{t}_{{{1}}}}\) has happened, so \({{t}_{{{2}}}}\) causally depends on \({{t}_{{{1}}}}\). If for transitions \({{t}_{{{1}}}}\) \(\ne \) \({{t}_{{{2}}}}\) neither \({{t}_{{{1}}}} < {{t}_{{{2}}}}\) nor \({{t}_{{{2}}}} < {{t}_{{{1}}}}\) holds, \({{t}_{{{1}}}}\) and \({{t}_{{{2}}}}\) are causally independent and can occur concurrently. Graphically, we represent these pomsets by showing each transition t labeled with \(\ell (t) = u\) as a box  and connecting these boxes with arcs representing the immediate causal successor relation \(<_m\) (see Fig. 2).
and connecting these boxes with arcs representing the immediate causal successor relation \(<_m\) (see Fig. 2).
Also, vice versa, if a concurrent trace \([(X,<,\ell )]\) is given, it is easy to construct a causal net \({\mathcal {N}_{{{}}}}\) corresponding to the trace in the above sense. One just has to add the missing places to turn the trace into a causal net.
3.3 Parallel Composition
Petri nets with disjoint sets of places, but possibly overlapping communication alphabets can be composed in parallel. Thereby transitions with different actions are performed asynchronously, whereas transitions with the same action synchronize. For  , i = 1,2, with \({{Pl}_{{{1}}}}\) \(\cap \) \({{Pl}_{{{2}}}}\) = \(\emptyset \) their parallel composition is defined as follows:
, i = 1,2, with \({{Pl}_{{{1}}}}\) \(\cap \) \({{Pl}_{{{2}}}}\) = \(\emptyset \) their parallel composition is defined as follows:

where

Note that actions labeled with the internal action \(\tau \) never synchronize because \(\tau \) does not appear in any communication alphabet \(A_i\).
Up to bijective renaming of places, the parallel composition of nets is commutative and associative, i.e., for all nets \(\mathcal {N}_1, \mathcal {N}_2, \mathcal {N}_3\):
4 Testing
The idea of testing processes is due to De Nicola and Hennessy [5, 11]. There the interaction of a (nondeterministic) process and a user is explicitly formalized using a synchronous parallel composition. The user is formalized by a test, which is a process with some states marked as a success. The authors distinguish between two options: a process may or must pass a test. A process P may pass a test T if in some maximal parallel computation with P, synchronizing on transitions with the same label, the test T reaches a success state. A process P must pass a test T if in all such computations the test T reaches a success state.
We transfer this notion of testing to Petri nets. A test is a Petri net, extended by a distinguished set  of successful places:
of successful places:  . In the graphical notation, we mark each place of this subset by the symbol
. In the graphical notation, we mark each place of this subset by the symbol  .
.
To perform a test \({\mathcal {T}_{{{}}}}\) on a given Petri net \({\mathcal {N}_{{{}}}}\), we consider the parallel composition \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\). A run \(\rho = ({\mathcal {N}_{{{R}}}}, f)\) of \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) is deadlock free if it is infinite, and it terminates successfully if it is finite and all places of \({\mathcal {T}_{{{}}}}\) inside the parallel composition without causal successor are marked with  . A net \({\mathcal {N}_{{{}}}}\) may pass a test \({\mathcal {T}_{{{}}}}\) if there exists a maximal run of \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) which is deadlock free or terminates successfully. A net \({\mathcal {N}_{{{}}}}\) must pass a test \({\mathcal {T}_{{{}}}}\) if all maximal runs of \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) are deadlock free or terminate successfully.
. A net \({\mathcal {N}_{{{}}}}\) may pass a test \({\mathcal {T}_{{{}}}}\) if there exists a maximal run of \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) which is deadlock free or terminates successfully. A net \({\mathcal {N}_{{{}}}}\) must pass a test \({\mathcal {T}_{{{}}}}\) if all maximal runs of \({\mathcal {N}_{{{}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) are deadlock free or terminate successfully.
To check a hyperproperty relating k concurrent traces on a system represented by a net \({\mathcal {N}_{{{0}}}}\), we investigate maximal runs \(\rho _i = ({\mathcal {N}_{{{i}}}}, f_i)\) with \(i = 1, \cdots , k\) of \({\mathcal {N}_{{{0}}}}\), where the causal nets \({\mathcal {N}_{{{i}}}}\) correspond to the concurrent traces of the hyperproperty, except that in \({\mathcal {N}_{{{i}}}}\) we relabel every action u of \({\mathcal {N}_{{{0}}}}\) into \(u_i\). We will test the parallel composition \({\mathcal {N}_{{{1}}}}\, \Vert \, \cdots \, \Vert \, {\mathcal {N}_{{{k}}}}\). The purpose of this relabeling is to have nets \({\mathcal {N}_{{{1}}}}, \dots , {\mathcal {N}_{{{k}}}}\) that do not synchronize in this composition. To represent the hyperproperty, we suitably quantify existentially or universally over these k runs of \({\mathcal {N}_{{{0}}}}\) and thus arrive at the following possibilities of testing:
where \(\mathcal {Q_i} \in \{\exists , \forall \}\) and \(\mathcal {m} \in \{\text {may, must}\}\). \({\mathcal {T}_{{{}}}}\) uses the subscripted labels of the form \(u_1, \dots , u_k\) to synchronize with the actions in \({\mathcal {N}_{{{1}}}}, \dots , {\mathcal {N}_{{{k}}}}\).
We also use primed copies like \(u'\) and \(u''\) instead of subscripts. For example, for \(k=2\), we use one causal net \({\mathcal {N}_{{{}}}}\) having the original actions of \({\mathcal {N}_{{{0}}}}\) and one causal \(\mathcal {N}'\) with every action u of \({\mathcal {N}_{{{0}}}}\) relabled into a primed copy \(u'\). Then the above pattern specializes to
where \(\mathcal {Q}, \mathcal {Q'} \in \{\exists , \forall \}\) and \(\mathcal {m} \in \{\text {may, must}\}\). Whereas \({\mathcal {N}_{{{}}}}\) and \(\mathcal {N}'\) have no common actions to synchronize on, the test \({\mathcal {T}_{{{}}}}\) will synchronize with \({\mathcal {N}_{{{}}}}\) and \(\mathcal {N}'\) via common (unprimed and primed) actions, thereby checking the hyperproperty. Note that the explicit quantifiers refer to runs of the system \({\mathcal {N}_{{{0}}}}\) under test. Once these runs are fixed, may and must corresponds to existential and universal quantification over runs originating from the test.
5 Examples
Left: Petri net \({\mathcal {N}_{{{1}}}}\) consists of two concurrent subnets, one performs only the low-security action l and the other has a choice starting with different high-security actions \(h_1\) and \(h_2\), but then performing the same low-security action \(l_1\), no matter whether \(h_1\) or \(h_2\) was chosen. Right: Petri net \({\mathcal {N}_{{{2}}}}\) looks identical to \({\mathcal {N}_{{{1}}}}\), but there is a subtle difference: the subnet on the right-hand side performs either \(l_1\) or \(l_2\) depending on the previous choice of \(h_1\) or \(h_2\), respectively.
We examine concurrent trace properties and concurrent hyperproperties for examples of concurrent systems. First consider the two Petri nets shown in Fig. 3. The net \({\mathcal {N}_{{{1}}}}\) consists of two concurrent subnets, one performs the low-security action l and the other has a choice starting with different high-security actions \(h_1\) and \(h_2\), but then both branches perform the same low-security action \(l_1\). The net \({\mathcal {N}_{{{2}}}}\) has the same structure, except that the choice in the subnet on the right-hand side is now between performing action \(l_1\) or action \(l_2\) depending on the previous choice of the high-security actions \(h_1\) or \(h_2\), respectively. Note that due to the choices, each of the nets \({\mathcal {N}_{{{1}}}}\) and \({\mathcal {N}_{{{2}}}}\) have two maximal runs, one with actions \(h_1\) and one with action \(h_2\).
Let us check the trace property whether the low-security action \(l_1\) can occur after l, independent of the high-security actions \(h_1\) and \(h_2\), To this end, we use the following test \({\mathcal {T}_{{{}}}}\):

This test is applied to each run of \({\mathcal {N}_{{{1}}}}\) and \({\mathcal {N}_{{{2}}}}\), respectively. We have
because \({\mathcal {T}_{{{}}}}\) terminates successfully for each of the two maximal runs, independent of the choice of \(h_1\) or \(h_2\). Here \({\mathcal {N}_{{{1,\rho }}}}\) denotes the net of the run \(\rho \) of \({\mathcal {N}_{{{1}}}}\).
For \({\mathcal {N}_{{{2}}}}\) the test \({\mathcal {T}_{{{}}}}\) is less successful. Let \({\mathcal {N}_{{{{2,h_1}}}}}\) and \({\mathcal {N}_{{{{2,h_2}}}}}\) be the nets for the two maximal runs of \({\mathcal {N}_{{{2}}}}\), depending on whether \(h_1\) or \(h_2\) is initially chosen. Then the parallel composition with \({\mathcal {T}_{{{}}}}\) yields the results shown in Fig. 4. Note that synchronization is enforced on the common actions l and \(l_1\), whereas \(h_1\) and \(h_2\) can occur asynchronously. In \({\mathcal {N}_{{{{2,h_1}}}}}\ \Vert \ {\mathcal {T}_{{{}}}}\), the test terminates successfully, whereas \({\mathcal {N}_{{{{2,h_2}}}}}\ \Vert \ {\mathcal {T}_{{{}}}}\) ends in a deadlock. Thus
but it is not the case that \(\forall \rho .\ {\mathcal {N}_{{{2,\rho }}}}\) must pass \({\mathcal {T}_{{{}}}}\). Here \({\mathcal {N}_{{{2,\rho }}}}\) denotes the net of the run \(\rho \) of \({\mathcal {N}_{{{2}}}}\).
Testing the two maximal runs of \({\mathcal {N}_{{{2}}}}\). In the middle, the places \(s_0, s_1, s_2\) of test \({\mathcal {T}_{{{}}}}\) in the parallel composition with these two runs are shown. Left: In \({\mathcal {N}_{{{{2,h_1}}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\), the test terminates successfully in \(s_2\). Right: However, \({\mathcal {N}_{{{{2,h_2}}}}}\, \Vert \, {\mathcal {T}_{{{}}}}\) ends in a deadlock, i.e., in places without  .
.
5.1 Testing the Concurrent Hyperproperties \(H_1\) and \(H_2\)
Next we turn to Sect. 1 and consider the three runs shown in Fig. 2 stemming from system \({\mathcal {N}_{{{C}}}}\) in Fig. 1. First we check with the sequential test \({\mathcal {T}_{{{ seq }}}}\) of Fig. 2 the concurrent hyperproperty whether every pair of concurrent traces \(\pi \) and \(\pi '\) agrees on the occurrence and ordering of the low-security events \(l_1\) and \(l_2\). This is property \(H_2\) in Example 2. Figure 5 shows the outcomes of testing \(\rho _1\) and \(\rho '_3\). We conclude that \(\rho _1\, \Vert \, \rho '_3\) may pass \({\mathcal {T}_{{{ seq }}}}\). More general, let \({\mathcal {N}_{{{}}}}\) and \(\mathcal {N}'\) be the nets of two runs \(\rho \) and \(\rho '\) corresponding to two traces \(\pi \) and \(\pi '\), respectively. If at least one of \(\rho \) and \(\rho '\) is instantiated with the concurrent run \(\rho _1\), we have \({\mathcal {N}_{{{}}}}\, \Vert \, \mathcal {N}' \text { may pass } {\mathcal {T}_{{{ seq }}}}\), otherwise \({\mathcal {N}_{{{}}}}\, \Vert \, \mathcal {N}' \text { may }{} not \text { pass } {\mathcal {T}_{{{ seq }}}}\). Summarizing, we have
and even
because we can instantiate \(\rho '\) with \(\rho _1\), but not \( \forall \, \rho , \rho '\, .\, {\mathcal {N}_{{{}}}}\, \Vert \, \mathcal {N}' \text { may pass } {\mathcal {T}_{{{ seq }}}}\). However, no must property holds for two concurrent traces and the test \({\mathcal {T}_{{{ seq }}}}\). This shows that the system \({\mathcal {N}_{{{C}}}}\) in Fig. 1 does not satisfy the concurrent hyperproperty \(H_2\).
Testing a concurrent hyperproperty with \({\mathcal {T}_{{{ seq }}}}\). We consider the two maximal runs of the parallel composition \(\rho _1\, \Vert \, {\mathcal {T}_{{{ seq }}}} \, \Vert \, \rho '_3\). Left: Here at first the alternative starting with \(l_2\) of the test \({\mathcal {T}_{{{ seq }}}}\) is chosen. This runs terminates successful. Right: Here at first the alternative starting with \(l_1\) of \({\mathcal {T}_{{{ seq }}}}\) is chosen. This runs ends in a deadlock because \(\rho _3\) engages first in \(l_2\).
Now we check with concurrent test \({\mathcal {T}_{{{ con }}}}\) of Fig. 2 the weaker concurrent hyperproperty whether every pair of concurrent traces \(\pi \) and \(\pi '\) agrees on the occurrence of the low-security events \(l_1\) and \(l_2\), i.e., each each \(l_1\) must be matched by \(l'_1\), but \(l_2\) may occur in between, and vice versa for \(l_2\) and \(l'_2\) and a possibly intervening \(l_1\). This is property \(H_1\) in Example 2. Figure 6 shows the outcomes of testing \(\rho _1\) and \(\rho _3\). We conclude that \(\rho _1\, \Vert \, \rho _3\) must pass \({\mathcal {T}_{{{ seq }}}}\). Indeed, we have
This shows that the system \({\mathcal {N}_{{{C}}}}\) in Fig. 1 satisfies the concurrent hyperproperty \(H_1\).
5.2 Testing the Concurrent Properties \(T_1\) and \(H_3\)
Consider the concurrent trace property \(T_1\) of Example 1 for a net \({\mathcal {N}_{{{,}}}}\) where a low-security event l must not depend on a high-security event h. We check this by requiring that
for the following test \({\mathcal {T}_{{{ hl }}}}\):

Testing a concurrent hyperproperty with \({\mathcal {T}_{{{ con }}}}\). We consider the unique maximal run of the parallel composition \(\rho _1\, \Vert \, {\mathcal {T}_{{{ con }}}} \, \Vert \, \rho '_3\). This run terminates successfully because both concurrent components of the test end in a place marked with  .
.
This test can terminate successfully after any (possibly empty) sequence of low-security events l. However, once a high-security event h occurs, the test terminates successfully only after any (possibly empty) sequence of further h events. Any low-security event l occurring after the first h will lead to a deadlock since the test does not offer any further synchronization on l.
Finally, we consider the concurrent hyperproperty \(H_3\) of generalized noninterference of Example 3. As low-security events we take \(l_1, l_2 \in \varSigma _ low \) and as high-security events \(h_1, h_2 \in \varSigma _ high \). The property is checked by requiring that
for the test \({\mathcal {T}_{{{ gni }}}}\) shown in Fig. 7.
In the two universally quantified runs \(\rho \) and \(\rho '\), this test uses labels \(l_1, l_2, h_1, h_2\) in the net \({\mathcal {N}_{{{}}}}\) of run \(\rho \) and copies \(l'_1, l'_2, h'_1, h'_2\) in the net \(\mathcal {N}'\) of \(\rho '\). Likewise, in the existentially quantified run \(\rho ''\), the test uses labels \(l''_1, l''_2, h''_1, h''_2\) in the net \(\mathcal {N}''\) of \(\rho ''\).
Note that the test \({\mathcal {T}_{{{ gni }}}}\) has an initial choice between the two internal \(\tau \) actions, but the conjunction in \(H_3\) is modeled by must testing, which requires that for each run \(\rho \) and \(\rho '\) both branches terminate with a success. In the left branch, the test is successful if it terminates when the low-security events \(l_1, l_2\) are matched by corresponding events \(l''_1, l''_2\), so that \(F_{ low }\) holds. The three transitions labeled h are shorthands for the occurrence of any event \(h_1, h_2, l_1', l_2', h_1', h_2',h_1'', h_2''\) that may intervene in this branch without any effect. In the right branch, the test is successful if it terminates when the high-security events \(h_1', h_2'\) are matched by corresponding events \(h''_1, h''_2\), so that \(G_{ high }\) holds. The three transitions labeled l are shorthands for the occurrence of any event \(l_1, l_2, h_1, h_2, l_1', l_2', l_1'', l_2''\) that may intervene in this branch without any effect.
6 Decidability
Universal must testing of a net \({\mathcal {N}_{{{0}}}}\) of the form
can be decided because their falsification is a reachability problem. Indeed, the negation of \((*)\) means that there exist k runs of \({\mathcal {N}_{{{0}}}}\) that composed in parallel with \({\mathcal {T}_{{{}}}}\) yield a finite net in which there exist places of \({\mathcal {T}_{{{}}}}\) without causal successor that are not marked with  . Instead of referring to k runs of \({\mathcal {N}_{{{0}}}}\) we can equivalently refer to k copies \({\mathcal {N}_{{{0,1}}}}, \dots , {\mathcal {N}_{{{0,k}}}}\) of \({\mathcal {N}_{{{0}}}}\), with suitably renamed action labels, and check the net \({\mathcal {N}_{{{}}}} = {\mathcal {N}_{{{0,1}}}}\, \Vert \, \cdots \, \Vert \, {\mathcal {N}_{{{0,k}}}}\, \Vert \ {\mathcal {T}_{{{}}}}\), with
. Instead of referring to k runs of \({\mathcal {N}_{{{0}}}}\) we can equivalently refer to k copies \({\mathcal {N}_{{{0,1}}}}, \dots , {\mathcal {N}_{{{0,k}}}}\) of \({\mathcal {N}_{{{0}}}}\), with suitably renamed action labels, and check the net \({\mathcal {N}_{{{}}}} = {\mathcal {N}_{{{0,1}}}}\, \Vert \, \cdots \, \Vert \, {\mathcal {N}_{{{0,k}}}}\, \Vert \ {\mathcal {T}_{{{}}}}\), with  as its transition relation and \({{Pl}_{{{{\mathcal {T}_{{{}}}}}}}}\) as the set of places inside \({\mathcal {T}_{{{}}}}\), for the following property:
as its transition relation and \({{Pl}_{{{{\mathcal {T}_{{{}}}}}}}}\) as the set of places inside \({\mathcal {T}_{{{}}}}\), for the following property:

This is a reachability problem for Petri nets, which is decidable [14]. Since we consider safe Petri nets, this reachablity is PSPACE-complete [6].
By contrast, universal may testing quickly gets undecidable.
Theorem 1
Universal may testing is undecidable for tests with two maximal runs.
Proof
We reduce the falsification of the Post Correspondence Problem (PCP) [22] to universal may testing using a test with two maximal runs. \(\square \)
We present the proof idea for the PCP over the alphabet \(\{a,b\}\). As an input, consider the set
of pairs of subwords, where
The PCP with this input is solvable by the correspondence (2, 3, 1, 3) because
The PCP input I is simulated by the Petri net \({\mathcal {N}_{{{I}}}}\) shown in Fig. 8. It consists of two branches that are selected by an initial choice between two internal actions. For distinguishing them in a test, the left branch starts with a transition labeled with u and the right branch with a transition labeled with v. Afterwards, their tokens reside in their center places from where they can nondeterministically choose which of the words \(u_i\) or \(v_i\) for \(i \in \{1,2,3\}\) to perform next. For example, the left branch simulates the subword \(u_1 = ab\) by the sequence of actions 1, a, and b, after which the token is again on the center place so that the next choice can be performed. After any finite number of choices each branch may stop its activity by performing the transition labeled with \( fu \) or \( fv \), respectively.
Test \({\mathcal {T}_{{{ PCP }}}}\) for checking whether two runs of \({\mathcal {N}_{{{}}}}\) do not simulate a correspondence of the PCP. The left branch ends in the place without  if the runs produce letter by letter the same word, the right branch ends in the place without
if the runs produce letter by letter the same word, the right branch ends in the place without  if the runs have chosen the same sequence of indices.
if the runs have chosen the same sequence of indices.
In general, the PCP with input I simulated by a net \({\mathcal {N}_{{{I}}}}\) of the form above has no correspondence if and only if
for the test \({\mathcal {T}_{{{ PCP }}}}\) shown in Fig. 9.
By contraposition, if the PCP has a correspondence, there exist maximal runs \(\rho \) and \(\rho '\) of \({\mathcal {N}_{{{I}}}}\) with nets \({\mathcal {N}_{{{}}}}\) and \(\mathcal {N}'\) such that the two maximal runs in \({\mathcal {N}_{{{}}}}\, \Vert \, \mathcal {N}'\, \Vert \, {\mathcal {T}_{{{ PCP }}}}\) stemming from the two branches in \({\mathcal {T}_{{{ PCP }}}}\) are not sucessful, i.e., each branch ends in the unique place that is not marked by  .
.
The left branch of \({\mathcal {T}_{{{ PCP }}}}\) ends in the place without  if \(\rho \) and \(\rho '\) produce letter by letter the same word. Here the transitions labeled with unprimed symbols refer to \(\rho \) and transitions labeled with primed symbols refer to \(\rho '\). The initial transitions labeled with u and \(v'\) ensure that the unprimed symbols refer to the left part of \({\mathcal {N}_{{{I}}}}\) simulating the u-part and that the primed symbols refer to (the primed version of) right part of \({\mathcal {N}_{{{I}}}}\) simulating the v-part of the proposed correspondence. Since the correspondence is finite, this branch of the test ends in the place without
if \(\rho \) and \(\rho '\) produce letter by letter the same word. Here the transitions labeled with unprimed symbols refer to \(\rho \) and transitions labeled with primed symbols refer to \(\rho '\). The initial transitions labeled with u and \(v'\) ensure that the unprimed symbols refer to the left part of \({\mathcal {N}_{{{I}}}}\) simulating the u-part and that the primed symbols refer to (the primed version of) right part of \({\mathcal {N}_{{{I}}}}\) simulating the v-part of the proposed correspondence. Since the correspondence is finite, this branch of the test ends in the place without  after performing \( fu \) and \( fv' \).
after performing \( fu \) and \( fv' \).
The right branch of \({\mathcal {T}_{{{ PCP }}}}\) ends in the place without  if \(\rho \) and \(\rho '\) have chosen the same sequence of indices 1, 2, 3 in producing the common word. Note that this branch checks the same runs \(\rho \) and \(\rho '\) than the left branch because \(\rho \) and \(\rho '\) are fixed initially.
if \(\rho \) and \(\rho '\) have chosen the same sequence of indices 1, 2, 3 in producing the common word. Note that this branch checks the same runs \(\rho \) and \(\rho '\) than the left branch because \(\rho \) and \(\rho '\) are fixed initially.
There is one technical detail. Whereas the runs \(\rho \) and \(\rho '\) have no symbols in common because \(\rho \) uses only unprimed symbols and \(\rho '\) only primed versions of the symbols, the test \({\mathcal {T}_{{{ PCP }}}}\) synchronizes in the parallel composition with \(\mathcal {N}\, \Vert \, \mathcal {N}'\) on all its symbols except \(\tau \), i.e., on \(a,b,a',b',u,v', fu , fv' , 1,2,3,1',2',3'\). To avoid unintended deadlocks we have to enable the left branch of \({\mathcal {T}_{{{ PCP }}}}\) to be able to synchronize at every place marked with 1 with any transition lableled with \(1,2,3,1',2'\) or \(3'\), and vice versa, the right branch of \({\mathcal {T}_{{{ PCP }}}}\) to be able to synchronize at every place marked with a with any transition lableled with \(a,b,a',b',u\) or \(v'\). To enhance visibility, we dropped the loop transitions attached to these places allowing for these synchronizations.
For the example input I, Fig. 10 shows two maximal runs of \({\mathcal {N}_{{{I}}}}\), one with the original symbols and one with primed symbols, that simulate the correspondence (2,3,1,3) and cause the test \({\mathcal {T}_{{{ PCP }}}}\) to end for each branch in the place that is not marked  .
.
7 Conclusion
We introduced the notion of concurrent hyperproperties as sets of sets of concurrent traces. This extends classical hyperproperties, which are sets of sets of traces. For analyzing concurrent hyperproperties, we used Petri nets as the underlying semantic model of concurrency. The analysis was performed by adapting may and must testing originally developed by DeNicola and Hennessy to our setting. Several examples illuminated the details of our approach.
As future work we envisage the introduction of suitable logics for specifying concurrent hyperproperties, extending HyperLTL for hyperproperties on traces (see [7] for an overview). A starting point could be event structure logic [18, 20].
References
Aichernig, B.K., He, J.: Refinement and test case generation in UTP. In: Aichernig, B.K., Boiten, E.A., Derrick, J., Groves, L. (eds.) Proceedings of the 11th Refinement Workshop, Refine@ICFEM 2006, Macao. Electronic Notes in Theoretical Computer Science, vol. 187, pp. 125–143. Elsevier (2006). https://doi.org/10.1016/j.entcs.2006.08.048
Best, E., Fernández, C.: Nonsequential Processes. Springer, Berlin (1988). https://doi.org/10.1007/978-3-642-73483-0
Busi, N., Gorrieri, R.: Structural non-interference in elementary and trace nets. Math. Struct. Comput. Sci. 19(6), 1065–1090 (2009). https://doi.org/10.1017/S0960129509990120
Clarkson, M.R., Schneider, F.B.: Hyperproperties. J. Comput. Secur. 18(6), 1157–1210 (2010). https://doi.org/10.3233/JCS-2009-0393
DeNicola, R., Hennessy, M.: Testing equivalences for processes. TCS 34, 83–134 (1984). https://doi.org/10.1016/0304-3975(84)90113-0
Esparza, J., Nielsen, M.: Decidability issues for Petri nets - a survey. Bull. EATCS 52, 244–262 (1994)
Finkbeiner, B.: Temporal hyperproperties. Bull. EATCS 123 (2017). http://eatcs.org/beatcs/index.php/beatcs/article/view/514
Goguen, J.A., Meseguer, J.: Security policies and security models. In: Proceedings of the IEEE Symposium on Security and Privacy, pp. 11–20. IEEE Computer Society (1982). https://doi.org/10.1109/SP.1982.10014
Goltz, U.: On representing CCS programs by finite petri nets. In: Chytil, M.P., Koubek, V., Janiga, L. (eds.) MFCS 1988. LNCS, vol. 324, pp. 339–350. Springer, Heidelberg (1988). https://doi.org/10.1007/BFb0017157
He, J., et al.: Provably correct systems. In: Langmaack, H., de Roever, W.-P., Vytopil, J. (eds.) FTRTFT 1994. LNCS, vol. 863, pp. 288–335. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58468-4_171
Hennessy, M.: Algebraic Theory of Processes. MIT Press, Cambridge (1988)
Hoare, C.A.R., He, J.: Unifying Theories of Programming. Prentice Hall, Hoboken (1998)
Hoare, C.: A model for communicating sequential processes. In: McKeag, R., MacNaughten, A. (eds.) On the Construction of Programs, pp. 229–254. Cambridge University Press (1980)
Mayr, E.W.: An algorithm for the general Petri net reachability problem. SIAM J. Comput. 13(3), 441–460 (1984). https://doi.org/10.1137/0213029
Mazurkiewicz, A.: Concurrent program schemes and their interpretations. DAIMI Rep. Ser. 6(78) (1977). https://doi.org/10.7146/dpb.v6i78.7691
McCullough, D.: Noninterference and the composability of security properties. In: Proceedings of the IEEE Symposium on Security and Privacy, pp. 177–186. IEEE Computer Society (1988). https://doi.org/10.1109/SECPRI.1988.8110
Milner, R.: A Calculus of Communicating Systems, LNCS, vol. 92. Springer, Berlin (1980). https://doi.org/10.1007/3-540-10235-3, http://link.springer.com/10.1007/3-540-10235-3
Mukund, M., Thiagarajan, P.S.: A logical characterization of well branching event structures. Theor. Comput. Sci. 96(1), 35–72 (1992). https://doi.org/10.1016/0304-3975(92)90181-E
Olderog, E.R.: Nets, Terms and Formulas: Three Views of Concurrent Processes and Their Relationship. Cambridge University Press, Cambridge (1991). https://doi.org/10.1017/CBO9780511526589
Penczek, W.: Branching time and partial order in temporal logics. In: Bolc, L., Szalas, A. (eds.) Time and Logics: A Computational Approach, pp. 203–257. UCL Press Ltd. (1995)
Petri, C.: Non-sequential processes. Technical Report. Internal Report GMD-ISF-77-5, Gesellschaft Math. Datenverarb., St. Augustin (1977)
Post, E.L.: A variant of a recursively unsolvable problem. Bull. Am. Math. Soc. 54(4), 264–268 (1946). https://doi.org/10.1007/978-3-642-19835-9
Pratt, V.R.: The pomset model of parallel processes: unifying the temporal and the spatial. In: Brookes, S.D., Roscoe, A.W., Winskel, G. (eds.) CONCURRENCY 1984. LNCS, vol. 197, pp. 180–196. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-15670-4
Reisig, W.: Petri Nets - An Introduction. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-69968-9
Su, T., Fu, Z., Pu, G., He, J., Su, Z.: Combining symbolic execution and model checking for data flow testing. In: Bertolino, A., Canfora, G., Elbaum, S.G. (eds.) 37th IEEE/ACM International Conference on Software Engineering, ICSE 2015, vol. 1, pp. 654–665. IEEE Computer Society (2015). https://doi.org/10.1109/ICSE.2015.81
Su, T., et al.: A survey on data-flow testing. ACM Comput. Surv. 50(1), 5:1–5:35 (2017). https://doi.org/10.1145/3020266
Winskel, G.: Event structures: Lecture notes for the Advanced Course on Petri Nets. Technical Report UCAM-CL-TR-95, University of Cambridge, Computer Laboratory (1986). https://www.cl.cam.ac.uk/techreports/UCAM-CL-TR-95.pdf
Acknowledgement
This work was supported by the European Research Council (ERC) Grant HYPER (No. 101055412).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Finkbeiner, B., Olderog, ER. (2023). Concurrent Hyperproperties. In: Bowen, J.P., Li, Q., Xu, Q. (eds) Theories of Programming and Formal Methods. Lecture Notes in Computer Science, vol 14080. Springer, Cham. https://doi.org/10.1007/978-3-031-40436-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-40436-8_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-40435-1
Online ISBN: 978-3-031-40436-8
eBook Packages: Computer ScienceComputer Science (R0)








 .
.  ,
,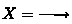 , the set of transitions of
, the set of transitions of 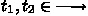 if
if 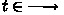 .
.






