Abstract
Multiparty session types (MSTs) are a type-based approach to verifying communication protocols. Central to MSTs is a projection operator: a partial function that maps protocols represented as global types to correct-by-construction implementations for each participant, represented as a communicating state machine. Existing projection operators are syntactic in nature, and trade efficiency for completeness. We present the first projection operator that is sound, complete, and efficient. Our projection separates synthesis from checking implementability. For synthesis, we use a simple automata-theoretic construction; for checking implementability, we present succinct conditions that summarize insights into the property of implementability. We use these conditions to show that MST implementability is PSPACE-complete. This improves upon a previous decision procedure that is in EXPSPACE and applies to a smaller class of MSTs. We demonstrate the effectiveness of our approach using a prototype implementation, which handles global types not supported by previous work without sacrificing performance.
E. Li and F. Stutz—equal contribution.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Protocol verification
- Multiparty session types
- Communicating state machines
- Protocol fidelity
- Deadlock freedom


1 Introduction
Communication protocols are key components in many safety and operation critical systems, making them prime targets for formal verification. Unfortunately, most verification problems for such protocols (e.g. deadlock freedom) are undecidable [11]. To make verification computationally tractable, several restrictions have been proposed [2, 3, 10, 14, 33, 42]. In particular, multiparty session types (MSTs) [24] have garnered a lot of attention in recent years (see, e.g., the survey by Ancona et al. [6]). In the MST setting, a protocol is specified as a global type, which describes the desired interactions of all roles involved in the protocol. Local implementations describe behaviors for each individual role. The implementability problem for a global type asks whether there exists a collection of local implementations whose composite behavior when viewed as a communicating state machine (CSM) matches that of the global type and is deadlock-free. The synthesis problem is to compute such an implementation from an implementable global type.
MST-based approaches typically solve synthesis and implementability simultaneously via an efficient syntactic projection operator [18, 24, 34, 41]. Abstractly, a projection operator is a partial map from global types to collections of implementations. A projection operator \(\texttt {proj}\) is sound when every global type \(\textbf{G}\) in its domain is implemented by \(\texttt {proj}(\textbf{G})\), and complete when every implementable global type is in its domain. Existing practical projection operators for MSTs are all incomplete (or unsound). Recently, the implementability problem was shown to be decidable for a class of MSTs via a reduction to safe realizability of globally cooperative high-level message sequence charts (HMSCs) [38]. In principle, this result yields a complete and sound projection operator for the considered class. However, this operator would not be practical. In particular, the proposed implementability check is in EXPSPACE.
Contributions. In this paper, we present the first practical sound and complete projection operator for general MSTs. The synthesis problem for implementable global types is conceptually easy [38] – the challenge lies in determining whether a global type is implementable. We thus separate synthesis from checking implementability. We first use a standard automata-theoretic construction to obtain a candidate implementation for a potentially non-implementable global type. However, unlike [38], we then verify the correctness of this implementation directly using efficiently checkable conditions derived from the global type. When a global type is not implementable, our constructive completeness proof provides a counterexample trace.
The resulting projection operator yields a PSPACE decision procedure for implementability. In fact, we show that the implementability problem is PSPACE-complete. These results both generalize and tighten the decidability and complexity results obtained in [38].
We evaluate a prototype of our projection algorithm on benchmarks taken from the literature. Our prototype benefits from both the efficiency of existing lightweight but incomplete syntactic projection operators [18, 24, 34, 41], and the generality of heavyweight automata-based model checking techniques [28, 36]: it handles protocols rejected by previous practical approaches while preserving the efficiency that makes MST-based techniques so attractive.
2 Motivation and Overview
Incompleteness of Existing Projection Operators. A key limitation of existing projection operators is that the implementation for each role is obtained via a linear traversal of the global type, and thus shares its structure. The following example, which is not projectable by any existing approach, demonstrates how enforcing structural similarity can lead to incompleteness.
Example 2.1
(Odd-even). Consider the following global type \(\textbf{G}_{oe}\):

A term  specifies the exchange of message \(m\) between sender
specifies the exchange of message \(m\) between sender  and receiver
and receiver  . The term represents two local events observed separately due to asynchrony: a send event
. The term represents two local events observed separately due to asynchrony: a send event  observed by role
observed by role  , and a receive event
, and a receive event  observed by role
observed by role  . The \(+\) operator denotes choice, \(\mu t.\, G\) denotes recursion, and 0 denotes protocol termination.
. The \(+\) operator denotes choice, \(\mu t.\, G\) denotes recursion, and 0 denotes protocol termination.
Figure 1a visualizes \(\textbf{G}_{oe}\) as an HMSC. The left and right sub-protocols respectively correspond to the top and bottom branches of the protocol. Role  chooses a branch by sending either
chooses a branch by sending either  or
or  to
to  . On the left,
. On the left,  echoes this message to
echoes this message to  . Both branches continue in the same way:
. Both branches continue in the same way:  sends an arbitrary number of
sends an arbitrary number of  messages to
messages to  , each of which is forwarded twice from
, each of which is forwarded twice from  to
to  . Role
. Role  signals the end of the loop by sending
signals the end of the loop by sending  to
to  , which
, which  forwards to
forwards to  . Finally, depending on the branch,
. Finally, depending on the branch,  must send
must send  or
or  to
to  .
.
Figures 1b and 1c depict the structural similarity between the global type \(\textbf{G}_{oe}\) and the implementations for  and
and  . For the “choicemaker” role
. For the “choicemaker” role  , the reason is evident. Role
, the reason is evident. Role  implementation collapses the continuations of both branches in the protocol into a single sub-component. For
implementation collapses the continuations of both branches in the protocol into a single sub-component. For  (Fig. 1d), the situation is more complicated. Role
(Fig. 1d), the situation is more complicated. Role  does not decide on or learn directly which branch is taken, but can deduce it from the parity of the number of
does not decide on or learn directly which branch is taken, but can deduce it from the parity of the number of  messages received from
messages received from  : odd means left and even means right. The resulting local implementation features transitions going back and forth between the two branches that do not exist in the global type. Syntactic projection operators fail to create such transitions. \(\blacktriangleleft \)
: odd means left and even means right. The resulting local implementation features transitions going back and forth between the two branches that do not exist in the global type. Syntactic projection operators fail to create such transitions. \(\blacktriangleleft \)
One response to the brittleness of existing projection operators has been to give up on global type specifications altogether and instead revert to model checking user-provided implementations [28, 36]. We posit that what needs rethinking is not the concept of global types, but rather how projections are computed and how implementability is checked.
Our Automata-Theoretic Approach. The synthesis step in our projection operator uses textbook automata-theoretic constructions. From a given global type, we derive a finite state machine, and use it to define a homomorphism automaton for each role. We then determinize this homomorphism automaton via subset construction to obtain a local candidate implementation for each role. If the global type is implementable, this construction always yields an implementation. The implementations shown in Figs. 1b to 1d are the result of applying this construction to \(\textbf{G}_{oe}\) from Example 2.1. Notice that the state labels in Fig. 1d correspond to sets of labels in the global protocol.
Unfortunately, not all global types are implementable.
High-level message sequence charts for the global types of Example 2.2.
Example 2.2
Consider the following four global types also depicted in Fig. 2:

Similar to \(\textbf{G}_{oe}\), in all four examples,  chooses a branch by sending either
chooses a branch by sending either  or
or  to
to  . The global type \(\textbf{G}_r\) is not implementable because
. The global type \(\textbf{G}_r\) is not implementable because  cannot learn which branch was chosen by
cannot learn which branch was chosen by  . For any local implementation of
. For any local implementation of  to be able to execute both branches, it must be able to receive
to be able to execute both branches, it must be able to receive  from
from  and
and  in any order. Because the two send events
in any order. Because the two send events  and
and  are independent of each other, they may be reordered. Consequently, any implementation of \(\textbf{G}_r\) would have to permit executions that are consistent with global behaviors not described by \(\textbf{G}_r\), such as
are independent of each other, they may be reordered. Consequently, any implementation of \(\textbf{G}_r\) would have to permit executions that are consistent with global behaviors not described by \(\textbf{G}_r\), such as  . Contrast this with \(\textbf{G}_r'\), which is implementable. In the top branch of \(\textbf{G}_r'\), role
. Contrast this with \(\textbf{G}_r'\), which is implementable. In the top branch of \(\textbf{G}_r'\), role  can only send to
can only send to  after it has received from
after it has received from  , which prevents the reordering of the send events
, which prevents the reordering of the send events  and
and  . The bottom branch is symmetric. Hence,
. The bottom branch is symmetric. Hence,  learns
learns  ’s choice based on which message it receives first.
’s choice based on which message it receives first.
For the global type \(\textbf{G}_s\), role  again cannot learn the branch chosen by
again cannot learn the branch chosen by  . That is,
. That is,  cannot know whether to send
cannot know whether to send  or
or  to
to  , leading inevitably to deadlocking executions. In contrast, \(\textbf{G}_s'\) is again implementable because the expected behavior of
, leading inevitably to deadlocking executions. In contrast, \(\textbf{G}_s'\) is again implementable because the expected behavior of  is independent of the choice by
is independent of the choice by  . \(\blacktriangleleft \)
. \(\blacktriangleleft \)
These examples show that the implementability question is non-trivial. To check implementability, we present conditions that precisely characterize when the subset construction for \(\textbf{G}\) yields an implementation.
Overview. The rest of the paper is organized as follows. Section 3 contains relevant definitions for our work. Section 4 describes the synthesis step of our projection. Section 5 presents the two conditions that characterize implementability of a given global type. In Sect. 6, we prove soundness of our projection via a stronger inductive invariant guaranteeing per-role agreement on a global run of the protocol. In Sect. 7, we prove completeness by showing that our two conditions hold if a global type is implementable. In Sect. 8, we discuss the complexity of our construction and condition checks. Section 9 presents our artifact and evaluation, and Sect. 10 as well as Sect. 11 discuss related work. Additional details including omitted proofs can be found in the extended version of the paper [29].
3 Preliminaries
Words. Let \(\varSigma \) be a finite alphabet. \(\varSigma ^*\) denotes the set of finite words over \(\varSigma \), \(\varSigma ^\omega \) the set of infinite words, and \(\varSigma ^\infty \negthinspace \) their union \(\varSigma ^* \cup \varSigma ^\omega \). A word \(u \in \varSigma ^*\) is a prefix of word \(v \in \varSigma ^\infty \), denoted \(u \le v\), if there exists \(w \in \varSigma ^\infty \) with \(u \cdot w = v\).
Message Alphabet. Let \(\mathcal {P}\) be a set of roles and \(\mathcal {V}\) be a set of messages. We define the set of synchronous events  where
where  denotes that message \(m\) is sent by
denotes that message \(m\) is sent by  to
to  atomically. This is split for asynchronous events. For a role
atomically. This is split for asynchronous events. For a role  , we define the alphabet
, we define the alphabet  of send events and the alphabet
of send events and the alphabet  of receive events. The event
of receive events. The event  denotes role
denotes role  sending a message \(m\) to
sending a message \(m\) to  , and
, and  denotes role
denotes role  receiving a message \(m\) from
receiving a message \(m\) from  . We write
. We write  ,
,  , and
, and  . Finally, \(\varSigma _{ async }= \varSigma _! \cup \varSigma _?\). We say that
. Finally, \(\varSigma _{ async }= \varSigma _! \cup \varSigma _?\). We say that  is active in \(x \in \varSigma _{ async }\) if
is active in \(x \in \varSigma _{ async }\) if  . For each role
. For each role  , we define a homomorphism
, we define a homomorphism  , where
, where  if
if  and \(\varepsilon \) otherwise. We write \(\mathcal {V}(w)\) to project the send and receive events in w onto their messages. We fix \(\mathcal {P}\) and \(\mathcal {V}\) in the rest of the paper.
and \(\varepsilon \) otherwise. We write \(\mathcal {V}(w)\) to project the send and receive events in w onto their messages. We fix \(\mathcal {P}\) and \(\mathcal {V}\) in the rest of the paper.
Global Types – Syntax. Global types for MSTs [31] are defined by the grammar:

where  range over \(\mathcal {P}\), \(m_i\) over \(\mathcal {V}\), and t over a set of recursion variables.
range over \(\mathcal {P}\), \(m_i\) over \(\mathcal {V}\), and t over a set of recursion variables.
We require each branch of a choice to be distinct:  , the sender and receiver of an atomic action to be distinct:
, the sender and receiver of an atomic action to be distinct:  , and recursion to be guarded: in \(\mu t. \, G\), there is at least one message between \(\mu t\) and each t in G. When \(|I| = 1\), we omit \(\sum \). For readability, we sometimes use the infix operator \(+\) for choice, instead of \(\sum \). When working with a protocol described by a global type, we write \(\textbf{G}\) to refer to the top-level type, and we use G to refer to its subterms. For the size of a global type, we disregard multiple occurrences of the same subterm.
, and recursion to be guarded: in \(\mu t. \, G\), there is at least one message between \(\mu t\) and each t in G. When \(|I| = 1\), we omit \(\sum \). For readability, we sometimes use the infix operator \(+\) for choice, instead of \(\sum \). When working with a protocol described by a global type, we write \(\textbf{G}\) to refer to the top-level type, and we use G to refer to its subterms. For the size of a global type, we disregard multiple occurrences of the same subterm.
We use the extended definition of global types from [31] that allows a sender to send messages to different roles in a choice. We call this sender-driven choice, as in [38], while it was called generalized choice in [31]. This definition subsumes classical MSTs that only allow directed choice [24]. The types we use focus on communication primitives and omit features like delegation or parametrization. We defer a detailed discussion of different MST frameworks to Sect. 11.
Global Types – Semantics. As a basis for the semantics of a global type \(\textbf{G}\), we construct a finite state machine \( \textsf{GAut}(\textbf{G}) = (Q_{\textbf{G}}, \varSigma _{ sync }, \delta _{\textbf{G}}, q_{0, \textbf{G}}, F_{\textbf{G}}) \) where
-
\(Q_{\textbf{G}}\) is the set of all syntactic subterms in \(\textbf{G}\) together with the term 0,
-
\(\delta _{\textbf{G}}\) is the smallest set containing
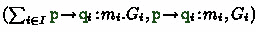 for each \(i \in I\), as well as \((\mu t. G', \varepsilon , G')\) and \((t, \varepsilon , \mu t. G')\) for each subterm \(\mu t.G'\),
for each \(i \in I\), as well as \((\mu t. G', \varepsilon , G')\) and \((t, \varepsilon , \mu t. G')\) for each subterm \(\mu t.G'\), -
\(q_{0, \textbf{G}} = \textbf{G}\) and \(F_{\textbf{G}} = \{0\}\).
We define a homomorphism \(\texttt {split}\) onto the asynchronous alphabet:

The semantics \(\mathcal {L}(\textbf{G})\) of a global type \(\textbf{G}\) is given by \(\mathcal {C}^{\sim }(\texttt {split}(\mathcal {L}(\textsf{GAut}(\textbf{G}))))\) where \(\mathcal {C}^{\sim }\) is the closure under the indistinguishability relation \(\sim \) [31]. Two events are independent if they are not related by the happened-before relation [26]. For instance, any two send events from distinct senders are independent. Two words are indistinguishable if one can be reordered into the other by repeatedly swapping consecutive independent events. The full definition is in the extended version [29].
Communicating State Machine [11]. is a CSM over \(\mathcal {P}\) and \(\mathcal {V}\) if
is a CSM over \(\mathcal {P}\) and \(\mathcal {V}\) if  is a finite state machine over
is a finite state machine over  for every
for every  , denoted by
, denoted by  . Let
. Let  denote the set of global states and
denote the set of global states and  denote the set of channels. A configuration of \(\mathcal {A}\) is a pair \((\vec {s}, \xi )\), where \(\vec {s}\,\) is a global state and \(\xi : \textsf{Chan}\rightarrow \mathcal {V}^*\) is a mapping from each channel to a sequence of messages. We use
denote the set of channels. A configuration of \(\mathcal {A}\) is a pair \((\vec {s}, \xi )\), where \(\vec {s}\,\) is a global state and \(\xi : \textsf{Chan}\rightarrow \mathcal {V}^*\) is a mapping from each channel to a sequence of messages. We use  to denote the state of
to denote the state of  in \(\vec {s}\). The CSM transition relation, denoted \(\rightarrow \), is defined as follows.
in \(\vec {s}\). The CSM transition relation, denoted \(\rightarrow \), is defined as follows.
-
 if
if  ,
,  ,
,  and \(\xi '(c) = \xi (c)\) for every other channel \(c\in \textsf{Chan}\).
and \(\xi '(c) = \xi (c)\) for every other channel \(c\in \textsf{Chan}\). -
 if
if  ,
,  ,
,  and \(\xi '(c) = \xi (c)\) for every other channel \(c\in \textsf{Chan}\).
and \(\xi '(c) = \xi (c)\) for every other channel \(c\in \textsf{Chan}\).
In the initial configuration \((\vec {s}_0, \xi _0)\), each role’s state in \(\vec {s}_0\) is the initial state  of
of  , and \(\xi _0\) maps each channel to \(\varepsilon \). A configuration \((\vec {s}, \xi )\) is said to be final iff
, and \(\xi _0\) maps each channel to \(\varepsilon \). A configuration \((\vec {s}, \xi )\) is said to be final iff  is final for every
is final for every  and \(\xi \) maps each channel to \(\varepsilon \). Runs and traces are defined in the expected way. A run is maximal if either it is finite and ends in a final configuration, or it is infinite. The language \(\mathcal {L}(\mathcal {A})\) of the CSM \(\mathcal {A}\) is defined as the set of maximal traces. A configuration \((\vec {s}, \xi )\) is a deadlock if it is not final and has no outgoing transitions. A CSM is deadlock-free if no reachable configuration is a deadlock.
and \(\xi \) maps each channel to \(\varepsilon \). Runs and traces are defined in the expected way. A run is maximal if either it is finite and ends in a final configuration, or it is infinite. The language \(\mathcal {L}(\mathcal {A})\) of the CSM \(\mathcal {A}\) is defined as the set of maximal traces. A configuration \((\vec {s}, \xi )\) is a deadlock if it is not final and has no outgoing transitions. A CSM is deadlock-free if no reachable configuration is a deadlock.
Finally, implementability is formalized as follows.
Definition 3.1
(Implementability [31]). A global type \(\textbf{G}\) is implementable if there exists a CSM  such that the following two properties hold:
such that the following two properties hold:
(i) protocol fidelity:  , and (ii) deadlock freedom:
, and (ii) deadlock freedom:  is deadlock-free. We say that
is deadlock-free. We say that  implements \(\textbf{G}\).
implements \(\textbf{G}\).
4 Synthesizing Implementations
The construction is carried out in two steps. First, for each role  , we define an intermediate state machine
, we define an intermediate state machine  that is a homomorphism of \(\textsf{GAut}(\textbf{G})\). We call
that is a homomorphism of \(\textsf{GAut}(\textbf{G})\). We call  the projection by erasure for
the projection by erasure for  , defined below.
, defined below.
Definition 4.1
(Projection by Erasure). Let \(\textbf{G}\) be some global type with its state machine \( \textsf{GAut}(\textbf{G}) = (Q_{\textbf{G}}, \varSigma _{ sync }, \delta _{\textbf{G}}, q_{0, \textbf{G}}, F_{\textbf{G}}) \). For each role  , we define the state machine
, we define the state machine  where
where  . By definition of \(\texttt {split}(\hbox {-})\), it holds that
. By definition of \(\texttt {split}(\hbox {-})\), it holds that  .
.
Then, we determinize  via a standard subset construction to obtain a deterministic local state machine for
via a standard subset construction to obtain a deterministic local state machine for  .
.
Definition 4.2
(Subset Construction). Let \(\textbf{G}\) be a global type and  be a role. Then, the subset construction for
be a role. Then, the subset construction for  is defined as
is defined as

-
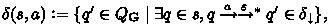 for every \(s \subseteq Q_{\textbf{G}}\) and
for every \(s \subseteq Q_{\textbf{G}}\) and 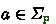
-
 ,
, -
 , and
, and -
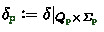
-

Note that the construction ensures that  only contains subsets of \(Q_{\textbf{G}}\) whose states are reachable via the same traces, i.e. we typically have
only contains subsets of \(Q_{\textbf{G}}\) whose states are reachable via the same traces, i.e. we typically have  .
.
The following characterization is immediate from the subset construction; the proof can be found in the extended version [29].
Lemma 4.3
Let \(\textbf{G}\) be a global type,  be a role, and
be a role, and  be its subset construction. If w is a trace of \(\textsf{GAut}(\textbf{G})\),
be its subset construction. If w is a trace of \(\textsf{GAut}(\textbf{G})\),  is a trace of
is a trace of  . If u is a trace of
. If u is a trace of  , there is a trace w of \(\textsf{GAut}(\textbf{G})\) such that
, there is a trace w of \(\textsf{GAut}(\textbf{G})\) such that  . It holds that
. It holds that  .
.
Using this lemma, we show that the CSM  preserves all behaviors of \(\textbf{G}\).
preserves all behaviors of \(\textbf{G}\).
Lemma 4.4
For all global types \(\textbf{G}\),  .
.
We briefly sketch the proof here. Given that  is deterministic, to prove language inclusion it suffices to prove the inclusion of the respective prefix sets:
is deterministic, to prove language inclusion it suffices to prove the inclusion of the respective prefix sets:

Let w be a word in \(\mathcal {L}(\textbf{G})\). If w is finite, membership in  is immediate from the claim above. If w is infinite, we show that w has an infinite run in
is immediate from the claim above. If w is infinite, we show that w has an infinite run in  using König’s Lemma. We construct an infinite graph \(\mathcal {G}_w(V, E)\) with \(V :=\{v_{\rho } \mid \texttt {trace}(\rho ) \le w\}\) and \(E :=\{(v_{\rho _1}, v_{\rho _2}) \mid \exists ~x \in \varSigma _{ async }.~\texttt {trace}(\rho _2) = \texttt {trace}(\rho _1)\cdot x\}\). Because
using König’s Lemma. We construct an infinite graph \(\mathcal {G}_w(V, E)\) with \(V :=\{v_{\rho } \mid \texttt {trace}(\rho ) \le w\}\) and \(E :=\{(v_{\rho _1}, v_{\rho _2}) \mid \exists ~x \in \varSigma _{ async }.~\texttt {trace}(\rho _2) = \texttt {trace}(\rho _1)\cdot x\}\). Because  is deterministic, \(\mathcal {G}_w\) is a tree rooted at \(v_\varepsilon \), the vertex corresponding to the empty run. By König’s Lemma, every infinite tree contains either a vertex of infinite degree or an infinite path. Because
is deterministic, \(\mathcal {G}_w\) is a tree rooted at \(v_\varepsilon \), the vertex corresponding to the empty run. By König’s Lemma, every infinite tree contains either a vertex of infinite degree or an infinite path. Because  consists of a finite number of communicating state machines, the last configuration of any run has a finite number of next configurations, and \(\mathcal {G}_w\) is finitely branching. Therefore, there must exist an infinite path in \(\mathcal {G}_w\) representing an infinite run for w, and thus
consists of a finite number of communicating state machines, the last configuration of any run has a finite number of next configurations, and \(\mathcal {G}_w\) is finitely branching. Therefore, there must exist an infinite path in \(\mathcal {G}_w\) representing an infinite run for w, and thus  .
.
The proof of the inclusion of prefix sets proceeds by structural induction and primarily relies on Lemma 4.3 and the fact that all prefixes in \(\mathcal {L}(\textbf{G})\) respect the order of send before receive events.
5 Checking Implementability
We now turn our attention to checking implementability of a CSM produced by the subset construction. We revisit the global types from Example 2.2 (also shown in Fig. 2), which demonstrate that the naive subset construction does not always yield a sound implementation. From these examples, we distill our conditions that precisely identify the implementable global types.
In general, a global type \(\textbf{G}\) is not implementable when the agreement on a global run of \(\textsf{GAut}(\textbf{G})\) among all participating roles cannot be conveyed via sending and receiving messages alone. When this happens, roles can take locally permitted transitions that commit to incompatible global runs, resulting in a trace that is not specified by \(\textbf{G}\). Consequently, our conditions need to ensure that when a role  takes a transition in
takes a transition in  , it only commits to global runs that are consistent with the local views of all other roles. We discuss the relevant conditions imposed on send and receive transitions separately.
, it only commits to global runs that are consistent with the local views of all other roles. We discuss the relevant conditions imposed on send and receive transitions separately.
Send Validity. Consider \(\textbf{G}_s\) from Example 2.2. The CSM  has an execution with the trace
has an execution with the trace  . This trace is possible because the initial state of
. This trace is possible because the initial state of  ,
,  , contains two states of
, contains two states of  , each of which has a single outgoing send transition labeled with
, each of which has a single outgoing send transition labeled with  and
and  respectively. Both of these transitions are always enabled in
respectively. Both of these transitions are always enabled in  , meaning that
, meaning that  can send
can send  even when
even when  has chosen the top branch and
has chosen the top branch and  expects to receive
expects to receive  instead of
instead of  from
from  . This results in a deadlock. In contrast, while the state
. This results in a deadlock. In contrast, while the state  in
in  likewise contains two states of
likewise contains two states of  , each with a single outgoing send transition, now both transitions are labeled with
, each with a single outgoing send transition, now both transitions are labeled with  . These two transitions collapse to a single one in
. These two transitions collapse to a single one in  . This transition is consistent with both possible local views that
. This transition is consistent with both possible local views that  and
and  might hold on the global run.
might hold on the global run.
Intuitively, to prevent the emergence of inconsistent local views from send transitions of  , we must enforce that for every state
, we must enforce that for every state  with an outgoing send transition labeled x, a transition labeled x must be enabled in all states of
with an outgoing send transition labeled x, a transition labeled x must be enabled in all states of  represented by s. We use the following auxiliary definition to formalize this intuition subsequently.
represented by s. We use the following auxiliary definition to formalize this intuition subsequently.
Definition 5.1
(Transition Origin and Destination). Let  be a transition in
be a transition in  and \(\delta _\downarrow \) be the transition relation of
and \(\delta _\downarrow \) be the transition relation of  . We define the set of transition origins \({\text {tr-orig}}(s \xrightarrow {x} s')\) and transition destinations \({\text {tr-dest}}(s \xrightarrow {x} s')\) as follows:
. We define the set of transition origins \({\text {tr-orig}}(s \xrightarrow {x} s')\) and transition destinations \({\text {tr-dest}}(s \xrightarrow {x} s')\) as follows:

Our condition on send transitions is then stated below.
Definition 5.2
(Send Validity). satisfies Send Validity iff every send transition
satisfies Send Validity iff every send transition  is enabled in all states contained in s:
is enabled in all states contained in s:

Receive Validity. To motivate our condition on receive transitions, let us revisit \(\textbf{G}_r\) from Example 2.2. The CSM  recognizes the following trace not in the global type language \(\mathcal {L}(\textbf{G}_r)\):
recognizes the following trace not in the global type language \(\mathcal {L}(\textbf{G}_r)\):

The issue lies with  which cannot distinguish between the two branches in \(\textbf{G}_r\). The initial state
which cannot distinguish between the two branches in \(\textbf{G}_r\). The initial state  of
of  has two states of \(\textsf{GAut}(\textbf{G}_r)\) corresponding to the subterms
has two states of \(\textsf{GAut}(\textbf{G}_r)\) corresponding to the subterms  and
and  . Here, \(G_t\) and \(G_b\) are the top and bottom branch of \(\textbf{G}_r\) respectively. This means that there are outgoing transitions in
. Here, \(G_t\) and \(G_b\) are the top and bottom branch of \(\textbf{G}_r\) respectively. This means that there are outgoing transitions in  labeled with
labeled with  and
and  . If
. If  takes the transition labeled
takes the transition labeled  , it commits to the bottom branch \(G_b\). However, observe that the message
, it commits to the bottom branch \(G_b\). However, observe that the message  from
from  can also be available at this time point if the other roles follow the top branch \(G_t\). This is because
can also be available at this time point if the other roles follow the top branch \(G_t\). This is because  can send
can send  to
to  without waiting for
without waiting for  to first receive from
to first receive from  . In this scenario, the roles disagree on which global run of \(\textsf{GAut}(\textbf{G}_r)\) to follow, resulting in the violating trace above.
. In this scenario, the roles disagree on which global run of \(\textsf{GAut}(\textbf{G}_r)\) to follow, resulting in the violating trace above.
Contrast this with \(\textbf{G}_r'\). Here,  again has outgoing transitions labeled with
again has outgoing transitions labeled with  and
and  . However, if
. However, if  takes the transition labeled
takes the transition labeled  , committing to the bottom branch, no disagreement occurs. This is because if the other roles are following the top branch, then
, committing to the bottom branch, no disagreement occurs. This is because if the other roles are following the top branch, then  is blocked from sending to
is blocked from sending to  until after it has received confirmation that
until after it has received confirmation that  has received its first message from
has received its first message from  .
.
For a receive transition \(s \xrightarrow {x} s_1\) in  to be safe, we must enforce that the receive event x cannot also be available due to reordered sent messages in the continuation \(G_2 \in s_2\) of another outgoing receive transition \(s \xrightarrow {y} s_2\). To formalize this condition, we use the set \(M^\mathcal {B}_{(G \ldots )}\) of available messages for a syntactic subterm G of \(\textbf{G}\) and a set of blocked roles \(\mathcal {B}\). This notion was already defined in [31, Sec. 2.2]. Intuitively, \(M^\mathcal {B}_{(G \ldots )}\) consists of all send events
to be safe, we must enforce that the receive event x cannot also be available due to reordered sent messages in the continuation \(G_2 \in s_2\) of another outgoing receive transition \(s \xrightarrow {y} s_2\). To formalize this condition, we use the set \(M^\mathcal {B}_{(G \ldots )}\) of available messages for a syntactic subterm G of \(\textbf{G}\) and a set of blocked roles \(\mathcal {B}\). This notion was already defined in [31, Sec. 2.2]. Intuitively, \(M^\mathcal {B}_{(G \ldots )}\) consists of all send events  that can occur on the traces of G such that \(m\) will be the first message added to channel
that can occur on the traces of G such that \(m\) will be the first message added to channel  before any of the roles in \(\mathcal {B}\) takes a step.
before any of the roles in \(\mathcal {B}\) takes a step.
Available Messages. The set of available messages is recursively defined on the structure of the global type. To obtain all possible messages, we need to unfold the distinct recursion variables once. For this, we define a map \( get\mu \) from variable to subterms and write \( get\mu _\textbf{G}\) for \( get\mu (\textbf{G})\):

The function \(M^{\mathcal {B}, T}_{(\hbox {-}\ldots )}\) keeps a set of unfolded variables T, which is empty initially.

We write \(M^{\mathcal {B}}_{(G \ldots )}\) for \(M^{\mathcal {B}, \emptyset }_{(G\ldots )}\). If \(\mathcal {B}\) is a singleton set, we omit set notation and write  for
for  . The set of available messages captures the possible states of all channels before a given receive transition is taken.
. The set of available messages captures the possible states of all channels before a given receive transition is taken.
Definition 5.3
(Receive Validity). satisfies Receive Validity iff no receive transition is enabled in an alternative continuation that originates from the same source state:
satisfies Receive Validity iff no receive transition is enabled in an alternative continuation that originates from the same source state:

Subset Projection. We are now ready to define our projection operator.
Definition 5.4
(Subset Projection of \(\textbf{G}\)). The subset projection  of \(\textbf{G}\) onto
of \(\textbf{G}\) onto  is
is  if it satisfies Send Validity and Receive Validity. We lift this operation to a partial function from global types to CSMs in the expected way.
if it satisfies Send Validity and Receive Validity. We lift this operation to a partial function from global types to CSMs in the expected way.
We conclude our discussion with an observation about the syntactic structure of the subset projection:
Send Validity implies that no state has both outgoing send and receive transitions (also known as mixed choice).
Corollary 5.5
(No Mixed Choice). If  satisfies Send Validity, then for all
satisfies Send Validity, then for all  , \(x_1 \in \varSigma _!\) iff \(x_2 \in \varSigma _!\).
, \(x_1 \in \varSigma _!\) iff \(x_2 \in \varSigma _!\).
6 Soundness
In this section, we prove the soundness of our subset projection, stated as follows.
Theorem 6.1
Let \(\textbf{G}\) be a global type and  be the subset projection. Then,
be the subset projection. Then,  implements \(\textbf{G}\).
implements \(\textbf{G}\).
Recall that implementability is defined as protocol fidelity and deadlock freedom. Protocol fidelity consists of two language inclusions. The first inclusion,  , enforces that the subset projection generates at least all behaviors of the global type. We showed in Lemma 4.4 that this holds for the subset construction alone (without Send and Receive Validity).
, enforces that the subset projection generates at least all behaviors of the global type. We showed in Lemma 4.4 that this holds for the subset construction alone (without Send and Receive Validity).
The second inclusion,  , enforces that no new behaviors are introduced. The proof of this direction relies on a stronger inductive invariant that we show for all traces of the subset projection. As discussed in Sect. 5, violations of implementability occur when roles commit to global runs that are inconsistent with the local views of other roles. Our inductive invariant states the exact opposite: that all local views are consistent with one another. First, we formalize the local view of a role.
, enforces that no new behaviors are introduced. The proof of this direction relies on a stronger inductive invariant that we show for all traces of the subset projection. As discussed in Sect. 5, violations of implementability occur when roles commit to global runs that are inconsistent with the local views of other roles. Our inductive invariant states the exact opposite: that all local views are consistent with one another. First, we formalize the local view of a role.
Definition 6.2
(Possible run sets). Let \(\textbf{G}\) be a global type and \(\textsf{GAut}(\textbf{G})\) be the corresponding state machine. Let  be a role and \(w \in \varSigma _{ async }^*\) be a word. We define the set of possible runs
be a role and \(w \in \varSigma _{ async }^*\) be a word. We define the set of possible runs  as all maximal runs of \(\textsf{GAut}(\textbf{G})\) that are consistent with
as all maximal runs of \(\textsf{GAut}(\textbf{G})\) that are consistent with  local view of w:
local view of w:

While Definition 6.2 captures the set of maximal runs that are consistent with the local view of a single role, we would like to refer to the set of runs that is consistent with the local view of all roles. We formalize this as the intersection of the possible run sets for all roles, which we denote as

With these definitions in hand, we can now formulate our inductive invariant:
Lemma 6.3
Let \(\textbf{G}\) be a global type and  be the subset projection. Let w be a trace of
be the subset projection. Let w be a trace of  . It holds that I(w) is non-empty.
. It holds that I(w) is non-empty.
The reasoning for the sufficiency of Lemma 6.3 is included in the proof of Theorem 6.1, found in the extended version [29]. In the rest of this section, we focus our efforts on how to show this inductive invariant, namely that the intersection of all roles’ possible run sets is non-empty.
We begin with the observation that the empty trace \(\varepsilon \) is consistent with all runs. As a result,  contains all maximal runs in \(\textsf{GAut}(\textbf{G})\). By definition, state machines for global types include at least one run, and the base case is trivially discharged. Intuitively, I(w) shrinks as more events are appended to w, but we show that at no point does it shrink to \(\emptyset \). We consider the cases where a send or receive event is appended to the trace separately, and show that the intersection set shrinks in a principled way that preserves non-emptiness. In fact, when a trace is extended with a receive event, Receive Validity guarantees that the intersection set does not shrink at all.
contains all maximal runs in \(\textsf{GAut}(\textbf{G})\). By definition, state machines for global types include at least one run, and the base case is trivially discharged. Intuitively, I(w) shrinks as more events are appended to w, but we show that at no point does it shrink to \(\emptyset \). We consider the cases where a send or receive event is appended to the trace separately, and show that the intersection set shrinks in a principled way that preserves non-emptiness. In fact, when a trace is extended with a receive event, Receive Validity guarantees that the intersection set does not shrink at all.
Lemma 6.4
Let \(\textbf{G}\) be a global type and  be the subset projection. Let wx be a trace of
be the subset projection. Let wx be a trace of  such that \(x \in \varSigma _?\). Then, \(I(w) = I(wx)\).
such that \(x \in \varSigma _?\). Then, \(I(w) = I(wx)\).
To prove this equality, we further refine our characterization of intersection sets. In particular, we show that in the receive case, the intersection between the sender and receiver’s possible run sets stays the same, i.e.

Note that it is not the case that the receiver only follows a subset of the sender’s possible runs. In other words,  is not inductive. The equality above simply states that a receive action can only eliminate runs that have already been eliminated by its sender. Figure 3 depicts this relation.
is not inductive. The equality above simply states that a receive action can only eliminate runs that have already been eliminated by its sender. Figure 3 depicts this relation.
Given that the intersection set strictly shrinks, the burden of eliminating runs must then fall upon send events. We show that send transitions shrink the possible run set of the sender in a way that is prefix-preserving. To make this more precise, we introduce the following definition on runs.
Definition 6.5
(Unique splitting of a possible run). Let \(\textbf{G}\) be a global type,  a role, and \(w \in \varSigma _{ async }^*\) a word. Let \(\rho \) be a possible run in
a role, and \(w \in \varSigma _{ async }^*\) a word. Let \(\rho \) be a possible run in  . We define the longest prefix of \(\rho \) matching w:
. We define the longest prefix of \(\rho \) matching w:

If \(\alpha ' \ne \rho \), we can split \(\rho \) into \( \rho = \alpha \cdot G \xrightarrow {l} G' \cdot \beta \) where \(\alpha ' = \alpha \cdot G\), \(G'\) denotes the state following G, and \(\beta \) denotes the suffix of \(\rho \) following \(\alpha \cdot G \cdot G'\). We call \(\alpha \cdot G \xrightarrow {l} G' \cdot \beta \) the unique splitting of \(\rho \) for  matching w. We omit the role
matching w. We omit the role  when obvious from context. This splitting is always unique because the maximal prefix of any
when obvious from context. This splitting is always unique because the maximal prefix of any  matching w is unique.
matching w is unique.
When role  fires a send transition
fires a send transition  , any run \(\rho = \alpha \cdot G \xrightarrow {l} G' \cdot \beta \) in
, any run \(\rho = \alpha \cdot G \xrightarrow {l} G' \cdot \beta \) in  possible run with
possible run with  is eliminated. While the resulting possible run set could no longer contain runs that end with \(G' \cdot \beta \), Send Validity guarantees that it must contain runs that begin with \(\alpha \cdot G\). This is formalized by the following lemma.
is eliminated. While the resulting possible run set could no longer contain runs that end with \(G' \cdot \beta \), Send Validity guarantees that it must contain runs that begin with \(\alpha \cdot G\). This is formalized by the following lemma.
Lemma 6.6
Let \(\textbf{G}\) be a global type and  be the subset projection. Let wx be a trace of
be the subset projection. Let wx be a trace of  such that
such that  for some
for some  . Let \(\rho \) be a run in I(w), and \(\alpha \cdot G \xrightarrow {l} G' \cdot \beta \) be the unique splitting of \(\rho \) for
. Let \(\rho \) be a run in I(w), and \(\alpha \cdot G \xrightarrow {l} G' \cdot \beta \) be the unique splitting of \(\rho \) for  with respect to w. Then, there exists a run \(\rho '\) in I(wx) such that \(\alpha \cdot G \le \rho '\).
with respect to w. Then, there exists a run \(\rho '\) in I(wx) such that \(\alpha \cdot G \le \rho '\).
This concludes our discussion of the send and receive cases in the inductive step to show the non-emptiness of the intersection of all roles’ possible run sets. The full proofs and additional definitions can be found in the extended version [29].
7 Completeness
In this section, we prove completeness of our approach. While soundness states that if a global type’s subset projection is defined, it then implements the global type, completeness considers the reverse direction.
Theorem 7.1
(Completeness). If \(\textbf{G}\) is implementable, then  is defined.
is defined.
We sketch the proof and refer to the extended version [29] for the full proof.
From the assumption that \(\textbf{G}\) is implementable, we know there exists a witness CSM that implements \(\textbf{G}\). While the soundness proof picks our subset projection as the existential witness for showing implementability – thereby allowing us to reason directly about a particular implementation – completeness only guarantees the existence of some witness CSM. We cannot assume without loss of generality that this witness CSM is our subset construction; however, we must use the fact that it implements \(\textbf{G}\) to show that Send and Receive Validity hold on our subset construction.
We proceed via proof by contradiction: we assume the negation of Send and Receive Validity for the subset construction, and show a contradiction to the fact that this witness CSM implements \(\textbf{G}\). In particular, we contradict protocol fidelity (Definition 3.1(i)), stating that the witness CSM generates precisely the language \(\mathcal {L}(\textbf{G})\). To do so, we exploit a simulation argument: we first show that the negation of Send and Receive Validity forces the subset construction to recognize a trace that is not a prefix of any word in \(\mathcal {L}(\textbf{G})\). Then, we show that this trace must also be recognized by the witness CSM, under the assumption that the witness CSM implements \(\textbf{G}\).
To highlight the constructive nature of our proof, we convert our proof obligation to a witness construction obligation. To contradict protocol fidelity, it suffices to construct a witness trace \(v_0\) satisfying two properties, where  is our witness CSM:
is our witness CSM:
-
(a)
\(v_0\) is a trace of
 , and
, and -
(b)
the run intersection set of \(v_0\) is empty:
 .
.
We first establish the sufficiency of conditions (a) and (b). Because  is deadlock-free by assumption, every prefix extends to a maximal trace. Thus, to prove the inequality of the two languages
is deadlock-free by assumption, every prefix extends to a maximal trace. Thus, to prove the inequality of the two languages  and \(\mathcal {L}(\textbf{G})\), it suffices to prove the inequality of their respective prefix sets. In turn, it suffices to show the existence of a prefix of a word in one language that is not a prefix of any word in the other. We choose to construct a prefix in the CSM language that is not a prefix in \(\mathcal {L}(\textbf{G})\). We again leverage the definition of intersection sets (Definition 6.2) to weaken the property of language non-membership to the property of having an empty intersection set as follows. By the semantics of \(\mathcal {L}(\textbf{G})\), for any \(w \in \mathcal {L}(\textbf{G})\), there exists \(w' \in \texttt {split}(\mathcal {L}(\textsf{GAut}(\textbf{G})))\) with \(w \sim w'\). For any \(w' \in \texttt {split}(\mathcal {L}(\textsf{GAut}(\textbf{G})))\), it trivially holds that \(w'\) has a non-empty intersection set. Because intersection sets are invariant under the indistinguishability relation \(\sim \), w must also have a non-empty intersection set. Since intersection sets are monotonically decreasing, if the intersection set of w is non-empty, then for any \(v \le w\), the intersection set of v is also non-empty. Modus tollens of the chain of reasoning above tells us that in order to show a word is not a prefix in \(\mathcal {L}(\textbf{G})\), it suffices to show that its intersection set is empty.
and \(\mathcal {L}(\textbf{G})\), it suffices to prove the inequality of their respective prefix sets. In turn, it suffices to show the existence of a prefix of a word in one language that is not a prefix of any word in the other. We choose to construct a prefix in the CSM language that is not a prefix in \(\mathcal {L}(\textbf{G})\). We again leverage the definition of intersection sets (Definition 6.2) to weaken the property of language non-membership to the property of having an empty intersection set as follows. By the semantics of \(\mathcal {L}(\textbf{G})\), for any \(w \in \mathcal {L}(\textbf{G})\), there exists \(w' \in \texttt {split}(\mathcal {L}(\textsf{GAut}(\textbf{G})))\) with \(w \sim w'\). For any \(w' \in \texttt {split}(\mathcal {L}(\textsf{GAut}(\textbf{G})))\), it trivially holds that \(w'\) has a non-empty intersection set. Because intersection sets are invariant under the indistinguishability relation \(\sim \), w must also have a non-empty intersection set. Since intersection sets are monotonically decreasing, if the intersection set of w is non-empty, then for any \(v \le w\), the intersection set of v is also non-empty. Modus tollens of the chain of reasoning above tells us that in order to show a word is not a prefix in \(\mathcal {L}(\textbf{G})\), it suffices to show that its intersection set is empty.
Having established the sufficiency of properties (a) and (b) for our witness construction, we present the steps to construct \(v_0\) from the negation of Send and Receive Validity respectively. We start by constructing a trace in  that satisfies (b), and then show that
that satisfies (b), and then show that  also recognizes the trace, thereby satisfying (a). In both cases, let
also recognizes the trace, thereby satisfying (a). In both cases, let  be the role and s be the state for which the respective validity condition is violated.
be the role and s be the state for which the respective validity condition is violated.
Send Validity (Definition 5.2). Let  be a transition such that
be a transition such that

First, we find a trace u of  that satisfies: (1) role
that satisfies: (1) role  is in state s in the CSM configuration reached via u, and (2) the run of \(\textsf{GAut}(\textbf{G})\) on u visits a state in
is in state s in the CSM configuration reached via u, and (2) the run of \(\textsf{GAut}(\textbf{G})\) on u visits a state in  . We obtain such a witness u from the \(\texttt {split}(\texttt {trace}(-))\) of a run prefix of \(\textsf{GAut}(\textbf{G})\) that ends in some state in
. We obtain such a witness u from the \(\texttt {split}(\texttt {trace}(-))\) of a run prefix of \(\textsf{GAut}(\textbf{G})\) that ends in some state in  . Any prefix thus obtained satisfies (1) by definition of
. Any prefix thus obtained satisfies (1) by definition of  , and satisfies (2) by construction. Due to the fact that send transitions are always enabled in a CSM,
, and satisfies (2) by construction. Due to the fact that send transitions are always enabled in a CSM,  must also be a trace of
must also be a trace of  , thus satisfying property (a) by a simulation argument. We then argue that
, thus satisfying property (a) by a simulation argument. We then argue that  satisfies property (b), stating that
satisfies property (b), stating that  is empty: the negation of Send Validity gives that there exist no run extensions from our candidate state in
is empty: the negation of Send Validity gives that there exist no run extensions from our candidate state in  with the immediate next action
with the immediate next action  , and therefore there exists no maximal run in \(\textsf{GAut}(\textbf{G})\) consistent with
, and therefore there exists no maximal run in \(\textsf{GAut}(\textbf{G})\) consistent with  .
.
Receive Validity (Definition 5.3). Let  and
and  be two transitions, and let
be two transitions, and let  such that
such that

Constructing the witness \(v_0\) pivots on finding a trace u of  such that both
such that both  and
and  are traces of
are traces of  . Equivalently, we show there exists a reachable configuration of
. Equivalently, we show there exists a reachable configuration of  in which
in which  can receive either message from distinct senders
can receive either message from distinct senders  and
and  . Formally, the local state of
. Formally, the local state of  has two outgoing states labeled with
has two outgoing states labeled with  and
and  , and the channels
, and the channels  and
and  have \(m_1\) and \(m_2\) at their respective heads. We construct such a u by considering a run in \(\textsf{GAut}(\textbf{G})\) that contains two transitions labeled with
have \(m_1\) and \(m_2\) at their respective heads. We construct such a u by considering a run in \(\textsf{GAut}(\textbf{G})\) that contains two transitions labeled with  and
and  . Such a run must exist due to the negation of Receive Validity. We start with the split trace of this run, and argue that, from the definition of \(M(\hbox {-})\) and the indistinguishability relation \(\sim \), we can perform iterative reorderings using \(\sim \) to bubble the send action
. Such a run must exist due to the negation of Receive Validity. We start with the split trace of this run, and argue that, from the definition of \(M(\hbox {-})\) and the indistinguishability relation \(\sim \), we can perform iterative reorderings using \(\sim \) to bubble the send action  to the position before the receive action
to the position before the receive action  . Then, (a) for
. Then, (a) for  holds by a simulation argument. We then separately show that (b) holds for
holds by a simulation argument. We then separately show that (b) holds for  using similar reasoning as the send case to complete the proof that
using similar reasoning as the send case to complete the proof that  suffices as a witness for \(v_0\).
suffices as a witness for \(v_0\).
It is worth noting that the construction of the witness prefix \(v_0\) in the proof immediately yields an algorithm for computing counterexample traces to implementability.
Remark 7.2
(Mixed Choice is Not Needed to Implement Global Types). Theorem 7.1 basically shows the necessity of Send Validity for implementability. Corollary 5.5 shows that Send Validity precludes states with both send and receive outgoing transitions. Together, this implies that an implementable global type can always be implemented without mixed choice. Note that the syntactic restrictions on global types do not inherently prevent mixed choice states from arising in a role’s subset construction, as evidenced by  in the following type:
in the following type:  Our completeness result thus implies that this type is not implementable. Most MST frameworks [18, 24, 31] implicitly force no mixed choice through syntactic restrictions on local types. We are the first to prove that mixed choice states are indeed not necessary for completeness. This is interesting because mixed choice is known to be crucial for the expressive power of the synchronous \(\pi \)-calculus compared to its asynchronous variant [32].
Our completeness result thus implies that this type is not implementable. Most MST frameworks [18, 24, 31] implicitly force no mixed choice through syntactic restrictions on local types. We are the first to prove that mixed choice states are indeed not necessary for completeness. This is interesting because mixed choice is known to be crucial for the expressive power of the synchronous \(\pi \)-calculus compared to its asynchronous variant [32].
8 Complexity
In this section, we establish PSPACE-completeness of checking implementability for global types.
Theorem 8.1
The MST implementability problem is PSPACE-complete.
Proof
We first establish the upper bound. The decision procedure enumerates for each role  the subsets of
the subsets of  . This can be done in polynomial space and exponential time. For each
. This can be done in polynomial space and exponential time. For each  and \(s \subseteq Q_{\textbf{G}}\), it then (i) checks membership of s in
and \(s \subseteq Q_{\textbf{G}}\), it then (i) checks membership of s in  of
of  , and (ii) if
, and (ii) if  , checks whether all outgoing transitions of s in
, checks whether all outgoing transitions of s in  satisfy Send and Receive Validity. Check (i) can be reduced to the intersection non-emptiness problem for nondeterministic finite state machines, which is in PSPACE [44]. It is easy to see that check (ii) can be done in polynomial time. In particular, the computation of available messages for Receive Validity only requires a single unfolding of every loop in \(\textbf{G}\).
satisfy Send and Receive Validity. Check (i) can be reduced to the intersection non-emptiness problem for nondeterministic finite state machines, which is in PSPACE [44]. It is easy to see that check (ii) can be done in polynomial time. In particular, the computation of available messages for Receive Validity only requires a single unfolding of every loop in \(\textbf{G}\).
Note that the synthesis problem has the same complexity. The subset construction to determinize  can be done using a PSPACE transducer. While the output can be of exponential size, it is written on an extra tape that is not counted towards memory usage. However, this means we need to perform the validity checks as described above instead of using the computed deterministic state machines.
can be done using a PSPACE transducer. While the output can be of exponential size, it is written on an extra tape that is not counted towards memory usage. However, this means we need to perform the validity checks as described above instead of using the computed deterministic state machines.
Second, we prove the lower bound. The proof is inspired by the proof for Theorem 4 [4] in which Alur et al. prove that checking safe realizability of bounded HMSCs is PSPACE-hard. We reduce the PSPACE-complete problem of checking universality of an NFA \(M = (Q, \varDelta , \delta , q_{0}, F)\) to checking implementability. Without loss of generality, we assume that every state can reach a final state. We construct a global type \(\textbf{G}\) for  and
and  that is implementable iff \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\). For this, we define subterms \(G_l\) and \(G_r\) as well as \(G_q\) for every \(q \in Q\) and \(G_{*}\). We use a fresh letter \(\bot \) to handle final states of M. We also define
that is implementable iff \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\). For this, we define subterms \(G_l\) and \(G_r\) as well as \(G_q\) for every \(q \in Q\) and \(G_{*}\). We use a fresh letter \(\bot \) to handle final states of M. We also define  as an abbreviation for
as an abbreviation for  .
.




The global type \(\textbf{G}\) is constructed such that  first decides whether words from \(\mathcal {L}(M)\) or from \(\varDelta ^{\negthinspace *}\) are sent subsequently. This decision is known to
first decides whether words from \(\mathcal {L}(M)\) or from \(\varDelta ^{\negthinspace *}\) are sent subsequently. This decision is known to  and
and  but not to
but not to  . The protocol then continues with
. The protocol then continues with  sending letters from \(\varDelta \) to
sending letters from \(\varDelta \) to  , and
, and  is not involved. Intuitively,
is not involved. Intuitively,  is able to receive these letters if and only if \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\). From Theorems 6.1 and 7.1, we know that
is able to receive these letters if and only if \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\). From Theorems 6.1 and 7.1, we know that  implements \(\textbf{G}\) if \(\textbf{G}\) is implementable.
implements \(\textbf{G}\) if \(\textbf{G}\) is implementable.
We claim that  implements \(\textbf{G}\) if and only if \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\).
implements \(\textbf{G}\) if and only if \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\).
First, assume that \(\mathcal {L}(M) \ne \varDelta ^{\negthinspace *}\). Then, there exists \(w \notin \mathcal {L}(M)\). We can construct the following run of  that deadlocks. Role
that deadlocks. Role  chooses the left subterm \(G_l\) and, subsequently,
chooses the left subterm \(G_l\) and, subsequently,  sends w to
sends w to  . We do a case analysis on whether w contains a prefix \(w'\) such that \(w' \notin {\text {pref}}(\mathcal {L}(M))\). If so, sending the last letter of a minimal prefix leads to a deadlock in
. We do a case analysis on whether w contains a prefix \(w'\) such that \(w' \notin {\text {pref}}(\mathcal {L}(M))\). If so, sending the last letter of a minimal prefix leads to a deadlock in  , contradicting deadlock freedom. If not, it holds that w is a prefix of a word in \(\mathcal {L}(M)\). Still, role
, contradicting deadlock freedom. If not, it holds that w is a prefix of a word in \(\mathcal {L}(M)\). Still, role  can send \(\bot \), which cannot be received, also contradicting deadlock freedom.
can send \(\bot \), which cannot be received, also contradicting deadlock freedom.
Second, assume that \(\mathcal {L}(M) = \varDelta ^{\negthinspace *}\). With this, it is fine that  does not know the branch. Role
does not know the branch. Role  will be able to receive all messages since
will be able to receive all messages since  can receive, letter by letter, \(w . \bot \) for every \(w \in \mathcal {L}(M)\) from
can receive, letter by letter, \(w . \bot \) for every \(w \in \mathcal {L}(M)\) from  . Thus, protocol fidelity and deadlock freedom hold, concluding the proof.
. Thus, protocol fidelity and deadlock freedom hold, concluding the proof.
Note that PSPACE-hardness only holds if the size of \(\textbf{G}\) does not account for common subterms multiple times. Because every message is immediately acknowledged, the constructed global type specifies a universally 1-bounded [23] language, proving that PSPACE-hardness persists for such a restriction. For our construction, it does not hold that  . We chose so to have a more compact protocol. However, we can easily fix this by sending the decision of
. We chose so to have a more compact protocol. However, we can easily fix this by sending the decision of  first to
first to  , allowing to omit the messages \(\bot \) to
, allowing to omit the messages \(\bot \) to  . \(\square \)
. \(\square \)
This result and the fact that local languages are preserved by the subset projection (Lemma 4.3) leads to the following observation.
Corollary 8.2
Let \(\textbf{G}\) be an implementable global type. Then, the subset projection  is a local language preserving implementation for \(\textbf{G}\), i.e.,
is a local language preserving implementation for \(\textbf{G}\), i.e.,  for every
for every  , and can be computed in PSPACE.
, and can be computed in PSPACE.
Remark 8.3
(MST implementability with directed choice is PSPACE-hard). Theorem 8.1 is stated for global types with sender-driven choice but the provided type is in fact directed. Thus, the PSPACE lower bound also holds for implementability of types with directed choice.
9 Evaluation
We consider the following three aspects in the evaluation of our approach: (E1) difficulty of implementation (E2) completeness, and (E3) comparison to state of the art.
For this, we implemented our subset projection in a prototype tool [1, 37]. It takes a global type as input and computes the subset projection for each role. It was straightforward to implement the core functionality in approximately 700 lines of Python3 code closely following the formalization (E1).
We consider global types (and communication protocols) from seven different sources as well as all examples from this work (cf. 1st column of Table 1). Our experiments were run on a computer with an Intel Core i7-1165G7 CPU and used at most 100MB of memory. The results are summarized in Table 1. The reported size is the number of states and transitions of the respective state machine, which allows not to account for multiple occurrences of the same subterm. As expected, our tool can project every implementable protocol we have considered (E2).
Regarding the comparison against the state of the art (E3), we directly compared our subset projection to the incomplete approach by Majumdar et al. [31], and found that the run times are in the same order of magnitude in general (typically a few milliseconds). However, the projection of [31] fails to project four implementable protocols (including Example 2.1). We discuss some of the other examples in more detail in the next section. We further note that most of the run times reported by Scalas and Yoshida [36] on their model checking based tool are around 1 s and are thus two to three orders of magnitude slower.
 or not
or not  , the time to compute our subset projection and the generalized projection by Majumdar et al. [31] as well as the outcome as
, the time to compute our subset projection and the generalized projection by Majumdar et al. [31] as well as the outcome as  for “implementable”,
for “implementable”,  for “not implementable” and (
for “not implementable” and ( ) for “not known”. We also give the size of the protocol (number of states and transitions), the number of roles, the combined size of all subset projections (number of states and transitions).
) for “not known”. We also give the size of the protocol (number of states and transitions), the number of roles, the combined size of all subset projections (number of states and transitions).10 Discussion
Success of Syntactic Projections Depends on Representation. Let us illustrate how unfolding recursion helps syntactic projection operators to succeed. Consider this implementable global type, which is not syntactically projectable:

Similar to projection by erasure, a syntactic projection erases events that a role is not involved in and immediately tries to merge different branches. The merge operator is a partial operator that checks sufficient conditions for implementability. Here, the merge operator fails for  because it cannot merge a recursion variable binder and a message reception. Unfolding the global type preserves the represented protocol and resolves this issue:
because it cannot merge a recursion variable binder and a message reception. Unfolding the global type preserves the represented protocol and resolves this issue:

(We refer to [29] for visual representations of both global types.) This global type can be projected with most syntactic projection operators and shows that the representation of the global type matters for syntactic projectability. However, such unfolding tricks do not always work, e.g. for the odd-even protocol (Example 2.1). We avoid this brittleness using automata and separating the synthesis from checking implementability.
Entailed Properties from the Literature. We defined implementability for a global type as the question of whether there exists a deadlock-free CSM that generates the same language as the global type. Various other properties of implementations and protocols have been proposed in the literature. Here, we give a brief overview and defer to the extended version [29] for a detailed analysis. Progress [18], a common property, requires that every sent message is eventually received and every expected message will eventually be sent. With deadlock freedom, our subset projection trivially satisfies progress for finite traces. For infinite traces, as expected, fairness assumptions are required to enforce progress. Similarly, our subset projection prevents unspecified receptions [14] and orphan messages [9, 21], respectively interpreted in our multiparty setting with sender-driven choice. We also ensure that every local transition of each role is executable [14], i.e. it is taken in some run of the CSM. Any implementation of a global type has the stable property [28], i.e., one can always reach a configuration with empty channels from every reachable configuration. While the properties above are naturally satisfied by our subset projection, the following ones can be checked directly on an implementable global type without explicitly constructing the implementation. A global type is terminating [36] iff it does not contain recursion and never-terminating [36] iff it does not contain term 0.
11 Related Work
MSTs were introduced by Honda et al. [24] with a process algebra semantics, and the connection to CSMs was established soon afterwards [20].
In this work, we present a complete projection procedure for global types with sender-driven choice. The work by Castagna et al. [13] is the only one to present a projection that aims for completeness. Their semantic conditions, however, are not effectively computable and their notion of completeness is “less demanding than the classical ones” [13]. They consider multiple implementations, generating different sets of traces, to be sound and complete with regard to a single global type [13, Sec. 5.3]. In addition, the algorithmic version of their conditions does not use global information as our message availability analysis does.
MST implementability relates to safe realizability of HMSCs, which is undecidable in general but decidable for certain classes [30]. Stutz [38] showed that implementability of global types that are always able to terminate is decidable.Footnote 1 The EXPSPACE decision procedure is obtained via a reduction to safe realizability of globally-cooperative HMSCs, by proving that the HMSC encoding [39] of any implementable global type is globally-cooperative and generalizing results for infinite executions. Thus, our PSPACE-completeness result both generalizes and tightens the earlier decidability result obtained in [38]. Stutz [38] also investigates how HMSC techniques for safe realizability can be applied to the MST setting – using the formal connection between MST implementability and safe realizability of HMSCs – and establishes an undecidability result for a variant of MST implementability with a relaxed indistinguishability relation.
Similar to the MST setting, there have been approaches in the HMSC literature that tie branching to a role making a choice. We refer the reader to the work by Majumdar et al. [31] for a survey.
Standard MST frameworks project a global type to a set of local types rather than a CSM. Local types are easily translated to FSMs [31, Def.11]. Our projection operator, though, can yield FSMs that cannot be expressed with the limited syntax of local types. Consider this implementable global type:  . The subset projection for
. The subset projection for  has two final states connected by a transition labeled
has two final states connected by a transition labeled  . In the syntax of local types, 0 is the only term indicating termination, which means that final states with outgoing transitions cannot be expressed. In contrast to the syntactic restrictions for global types, which are key to effective verification, we consider local types unnecessarily restrictive. Usually, local implementations are type-checked against their local types and subtyping gives some implementation freedom [12, 16, 17, 27]. However, one can also view our subset projection as a local specification of the actual implementation. We conjecture that subtyping would then amount to a variation of alternating refinement [5].
. In the syntax of local types, 0 is the only term indicating termination, which means that final states with outgoing transitions cannot be expressed. In contrast to the syntactic restrictions for global types, which are key to effective verification, we consider local types unnecessarily restrictive. Usually, local implementations are type-checked against their local types and subtyping gives some implementation freedom [12, 16, 17, 27]. However, one can also view our subset projection as a local specification of the actual implementation. We conjecture that subtyping would then amount to a variation of alternating refinement [5].
CSMs are Turing-powerful [11] but decidable classes were obtained for different semantics: restricted communication topology [33, 42], half-duplex communication (only for two roles) [14], input-bounded [10], and unreliable channels [2, 3]. Global types (as well choreography automata [7]) can only express existentially 1-bounded, 1-synchronizable and half-duplex communication [39]. Key to this result is that sending and receiving a message is specified atomically in a global type — a feature Dagnino et al. [19] waived for their deconfined global types. However, Dagnino et al. [19] use deconfined types to capture the behavior of a given system rather than projecting to obtain a system that generates specified behaviors.
This work relies on reliable communication as is standard for MST frameworks. Work on fault-tolerant MST frameworks [8, 43] attempts to relax this restriction. In the setting of reliable communication, both context-free [25, 40] and parametric [15, 22] versions of session types have been proposed to capture more expressive protocols and entire protocol families respectively. Extending our approach to these generalizations is an interesting direction for future work.
Notes
- 1.
This syntactic restriction is referred to as 0-reachability in [38].
References
Prototype Implementation of Subset Projection for Multiparty Session Types. https://gitlab.mpi-sws.org/fstutz/async-mpst-gen-choice/
Abdulla, P.A., Aiswarya, C., Atig, M.F.: Data communicating processes with unreliable channels. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science, LICS ’16, New York, NY, USA, 5–8 July 2016, pp. 166–175. ACM (2016). https://doi.org/10.1145/2933575.2934535
Abdulla, P.A., Bouajjani, A., Jonsson, B.: On-the-fly analysis of systems with unbounded, lossy FIFO channels. In: Hu, A.J., Vardi, M.Y. (eds.) CAV 1998. LNCS, vol. 1427, pp. 305–318. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0028754
Alur, R., Etessami, K., Yannakakis, M.: Realizability and verification of MSC graphs. Theor. Comput. Sci. 331(1), 97–114 (2005). https://doi.org/10.1016/j.tcs.2004.09.034
Alur, R., Henzinger, T.A., Kupferman, O., Vardi, M.Y.: Alternating refinement relations. In: Sangiorgi, D., de Simone, R. (eds.) CONCUR 1998. LNCS, vol. 1466, pp. 163–178. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055622
Ancona, D., et al.: Behavioral types in programming languages. Found. Trends Program. Lang. 3(2-3), 95–230 (2016). https://doi.org/10.1561/2500000031
Barbanera, F., Lanese, I., Tuosto, E.: Choreography automata. In: Bliudze, S., Bocchi, L. (eds.) COORDINATION 2020. LNCS, vol. 12134, pp. 86–106. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-50029-0_6
Barwell, A.D., Scalas, A., Yoshida, N., Zhou, F.: Generalised multiparty session types with crash-stop failures. In: Klin, B., Lasota, S., Muscholl, A. (eds.) 33rd International Conference on Concurrency Theory, CONCUR 2022, 12–16 September 2022, Warsaw, Poland. LIPIcs, vol. 243, pp. 35:1–35:25. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022). https://doi.org/10.4230/LIPIcs.CONCUR.2022.35
Bocchi, L., Lange, J., Yoshida, N.: Meeting deadlines together. In: Aceto, L., de Frutos-Escrig, D. (eds.) 26th International Conference on Concurrency Theory, CONCUR 2015, Madrid, Spain, 1–4 September 2015. LIPIcs, vol. 42, pp. 283–296. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2015). https://doi.org/10.4230/LIPIcs.CONCUR.2015.283
Bollig, B., Finkel, A., Suresh, A.: Bounded reachability problems are decidable in FIFO machines. In: Konnov, I., Kovács, L. (eds.) 31st International Conference on Concurrency Theory, CONCUR 2020, 1–4 September 2020, Vienna, Austria (Virtual Conference). LIPIcs, vol. 171, pp. 49:1–49:17. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020). https://doi.org/10.4230/LIPIcs.CONCUR.2020.49
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983). https://doi.org/10.1145/322374.322380
Bravetti, M., Carbone, M., Zavattaro, G.: On the boundary between decidability and undecidability of asynchronous session subtyping. Theor. Comput. Sci. 722, 19–51 (2018). https://doi.org/10.1016/j.tcs.2018.02.010
Castagna, G., Dezani-Ciancaglini, M., Padovani, L.: On global types and multi-party session. Log. Methods Comput. Sci. 8(1) (2012). https://doi.org/10.2168/LMCS-8(1:24)2012
Cécé, G., Finkel, A.: Verification of programs with half-duplex communication. Inf. Comput. 202(2), 166–190 (2005). https://doi.org/10.1016/j.ic.2005.05.006
Charalambides, M., Dinges, P., Agha, G.A.: Parameterized, concurrent session types for asynchronous multi-actor interactions. Sci. Comput. Program. 115-116, 100–126 (2016). https://doi.org/10.1016/j.scico.2015.10.006
Chen, T., Dezani-Ciancaglini, M., Scalas, A., Yoshida, N.: On the preciseness of subtyping in session types. Log. Methods Comput. Sci. 13(2) (2017). https://doi.org/10.23638/LMCS-13(2:12)2017
Chen, T., Dezani-Ciancaglini, M., Yoshida, N.: On the preciseness of subtyping in session types. In: Chitil, O., King, A., Danvy, O. (eds.) Proceedings of the 16th International Symposium on Principles and Practice of Declarative Programming, Kent, Canterbury, United Kingdom, 8–10, September 2014. pp. 135–146. ACM (2014). https://doi.org/10.1145/2643135.2643138
Coppo, M., Dezani-Ciancaglini, M., Padovani, L., Yoshida, N.: A gentle introduction to multiparty asynchronous session types. In: Bernardo, M., Johnsen, E.B. (eds.) SFM 2015. LNCS, vol. 9104, pp. 146–178. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18941-3_4
Dagnino, F., Giannini, P., Dezani-Ciancaglini, M.: Deconfined global types for asynchronous sessions. In: Damiani, F., Dardha, O. (eds.) COORDINATION 2021. LNCS, vol. 12717, pp. 41–60. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-78142-2_3
Deniélou, P.-M., Yoshida, N.: Multiparty session types meet communicating automata. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 194–213. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_10
Deniélou, P.-M., Yoshida, N.: Multiparty compatibility in communicating automata: characterisation and synthesis of global session types. In: Fomin, F.V., Freivalds, R., Kwiatkowska, M., Peleg, D. (eds.) ICALP 2013. LNCS, vol. 7966, pp. 174–186. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39212-2_18
Deniélou, P., Yoshida, N., Bejleri, A., Hu, R.: Parameterised multiparty session types. Log. Methods Comput. Sci. 8(4) (2012). https://doi.org/10.2168/LMCS-8(4:6)2012
Genest, B., Kuske, D., Muscholl, A.: On communicating automata with bounded channels. Fundam. Inform. 80(1–3), 147–167 (2007). http://content.iospress.com/articles/fundamenta-informaticae/fi80-1-3-09
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: Necula, G.C., Wadler, P. (eds.) Proceedings of the 35th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2008, San Francisco, California, USA, 7–12 January 2008, pp. 273–284. ACM (2008). https://doi.org/10.1145/1328438.1328472
Keizer, A.C., Basold, H., Pérez, J.A.: Session coalgebras: a coalgebraic view on regular and context-free session types. ACM Trans. Program. Lang. Syst. 44(3), 18:1–18:45 (2022). https://doi.org/10.1145/3527633
Lamport, L.: Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978). https://doi.org/10.1145/359545.359563
Lange, J., Yoshida, N.: On the undecidability of asynchronous session subtyping. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 441–457. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_26
Lange, J., Yoshida, N.: Verifying asynchronous interactions via communicating session automata. In: Dillig, I., Tasiran, S. (eds.) CAV 2019. LNCS, vol. 11561, pp. 97–117. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25540-4_6
Li, E., Stutz, F., Wies, T., Zufferey, D.: Complete multiparty session type projection with automata. CoRR abs/2305.17079 (2023). https://doi.org/10.48550/arXiv.2305.17079
Lohrey, M.: Realizability of high-level message sequence charts: closing the gaps. Theor. Comput. Sci. 309(1-3), 529–554 (2003). https://doi.org/10.1016/j.tcs.2003.08.002
Majumdar, R., Mukund, M., Stutz, F., Zufferey, D.: Generalising projection in asynchronous multiparty session types. In: Haddad, S., Varacca, D. (eds.) 32nd International Conference on Concurrency Theory, CONCUR 2021, 24–27 August 2021, Virtual Conference. LIPIcs, vol. 203, pp. 35:1–35:24. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.CONCUR.2021.35
Palamidessi, C.: Comparing the expressive power of the synchronous and asynchronous pi-calculi. Math. Struct. Comput. Sci. 13(5), 685–719 (2003). https://doi.org/10.1017/S0960129503004043
Peng, W., Purushothaman, S.: Analysis of a class of communicating finite state machines. Acta Informatica 29(6/7), 499–522 (1992). https://doi.org/10.1007/BF01185558
Scalas, A., Dardha, O., Hu, R., Yoshida, N.: A linear decomposition of multiparty sessions for safe distributed programming. In: Müller, P. (ed.) 31st European Conference on Object-Oriented Programming, ECOOP 2017, 19–23 June 2017, Barcelona, Spain. LIPIcs, vol. 74, pp. 24:1–24:31. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2017). https://doi.org/10.4230/LIPIcs.ECOOP.2017.24
Scalas, A., Yoshida, N.: Mpstk: the multiparty session types toolkit (2018). https://doi.org/10.1145/3291638
Scalas, A., Yoshida, N.: Less is more: multiparty session types revisited. Proc. ACM Program. Lang. 3(POPL), 30:1–30:29 (2019). https://doi.org/10.1145/3290343
Stutz, F.: Artifact for “Complete Multiparty Session Type Projection with Automata”, April 2023. https://doi.org/10.5281/zenodo.7878493
Stutz, F.: Asynchronous multiparty session type implementability is decidable - lessons learned from message sequence charts. In: 37th European Conference on Object-Oriented Programming, ECOOP 2023. LIPIcs (2023). https://arxiv.org/pdf/2302.11272.pdf
Stutz, F., Zufferey, D.: Comparing channel restrictions of communicating state machines, high-level message sequence charts, and multiparty session types. In: Ganty, P., Monica, D.D. (eds.) Proceedings of the 13th International Symposium on Games, Automata, Logics and Formal Verification, GandALF 2022, Madrid, Spain, 21–23 September 2022. EPTCS, vol. 370, pp. 194–212 (2022). https://doi.org/10.4204/EPTCS.370.13
Thiemann, P., Vasconcelos, V.T.: Context-free session types. In: Garrigue, J., Keller, G., Sumii, E. (eds.) Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, ICFP 2016, Nara, Japan, 18–22 September 2016, pp. 462–475. ACM (2016). https://doi.org/10.1145/2951913.2951926
Toninho, B., Yoshida, N.: Certifying data in multiparty session types. J. Log. Algebraic Methods Program. 90, 61–83 (2017). https://doi.org/10.1016/j.jlamp.2016.11.005
La Torre, S., Madhusudan, P., Parlato, G.: Context-bounded analysis of concurrent queue systems. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 299–314. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_21
Viering, M., Hu, R., Eugster, P., Ziarek, L.: A multiparty session typing discipline for fault-tolerant event-driven distributed programming. Proc. ACM Program. Lang. 5(OOPSLA), 1–30 (2021). https://doi.org/10.1145/3485501
Wehar, M.: On the complexity of intersection non-emptiness problems. Ph.D. thesis, University of Buffalo (2016)
Spring and Hibernate Transaction in Java. https://www.uml-diagrams.org/examples/spring-hibernate-transaction-sequence-diagram-example.html
Acknowledgements
This work is funded in part by the National Science Foundation under grant 1815633. Felix Stutz was supported by the Deutsche Forschungsgemeinschaft project 389792660 TRR 248—CPEC.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Li, E., Stutz, F., Wies, T., Zufferey, D. (2023). Complete Multiparty Session Type Projection with Automata. In: Enea, C., Lal, A. (eds) Computer Aided Verification. CAV 2023. Lecture Notes in Computer Science, vol 13966. Springer, Cham. https://doi.org/10.1007/978-3-031-37709-9_17
Download citation
DOI: https://doi.org/10.1007/978-3-031-37709-9_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-37708-2
Online ISBN: 978-3-031-37709-9
eBook Packages: Computer ScienceComputer Science (R0)







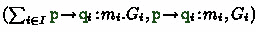 for each
for each  if
if  ,
,  ,
,  and
and  if
if  ,
,  ,
,  and
and 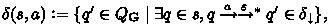 for every
for every 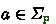
 ,
, , and
, and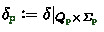


 sends a message
sends a message  receives it.
receives it. , and
, and .
.