Keywords

On the History of Developmental Education: The Case of Mathematical Thinking

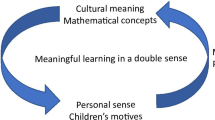
In the Netherlands we have been working since the 1980s at the implementation of a curriculum for primary education, called Developmental Education. This curriculum aims at a broad identity development of pupils and teachers and requires that all learning should be culturally meaningful and make personal sense for the learners. In this way, we (i.e., the teachers, teacher trainers, researchers) aim at enabling pupils to become agentive critical participants in all kinds of cultural practices. Developmental Education is not a mandatory curriculum in the Netherlands: every school is free to opt for this approach or not, and can get funding from the government for its implementation and professionalization of its teachers.

Developmental Education is based on Vygotskij’s cultural-historical theory of human development, elaborated with Leont’ev’s Activity Theory and El’konin’s theory of child development (El’konin, 1978; Leont’ev, 1978; van Oers, 2012a; Vygotsky, 1978). On the basis of this Cultural-Historical Activity Theory (CHAT), it is assumed that higher psychological functions emerge from meaningful interactions with adults or more knowledgeable peers. Rather than being naturally emerging and waiting for maturation stimulated by experiences with the outside world, psychological functions develop in a process of a person’s enculturation that starts out from participation and communication with more knowledgeable others in cultural practices that make sense for them, such as household, hospital, supermarket, museum, post-office, library, artist studio, gardening, etc. Due to this meaningfulness, children are mostly interested to be engaged in these well-known activities, and are willing to acquire new actions with new cultural means (like instrumental tools or concepts, etcetera) to make it look ‘like the real world’ for them. Participation in real life cultural practices always requires the adoption of a specific role within that practice, and eventually it calls for the appropriation of the tools that are constitutive for this role, like for instance a stethoscope for a doctor, measuring devices and numbers for a gardener or carpenter, symbolic representations for mathematicians. Tools are unavoidable for enacting a role in a cultural practice. As Vygotskij has pointed out, language is an essential tool for executing context-based actions and cognitive functions and for communicating with others and oneself about tool use in specific situations (e.g., Vygotskij, 1982/1934).

In this article, I want to focus on the emergence of mathematical thinking as a meaningful activity, that is to say as a cultural activity that has cultural relevance and also makes sense for the learner. Studying the genesis of mathematical thinking (as in this article) first of all implies that we have to explain how ‘mathematics’ enters into the child’s mind in the first place. In one of his books on child development, Vygotskij (1984, pp. 226–227) explains this in general terms as steps in the process of development of children’s consciousness. Freely summarized here in terms of an emerging mathematical consciousness, this process can also be sketched as a result of the interaction of a child and an adult. As a first step, the child is acting spontaneously with objects in his environment, often on the basis of exploratory needs but also on the basis of imitations of significant others. In this stage the children may be reciting number words, but this action is not yet ‘mathematical’ for them, although it may look like that from an adult perspective (Munn, 1997, p. 16). These ‘counting’- acts and included objects at first do not have specific intellectual meanings for the child beyond the fact that she/he wants to manipulate the objects and by so doing look like the surrounding adults. The observing adult then may interpret this in terms of her/his own cultural cognitive system and (for example) mention the name of the object or of the act carried out on this object. This is the second step: the act and object by themselves are then turned into a shared topic that can be enriched by the adult by adding new meanings (‘predicates’). This is the moment that mathematical qualifications enter the consciousness of the child. The child hears and may repeat ‘ten’, ‘count’, ‘number’, or ‘more’ etcetera. Finally, in due time, the child may begin using these new meanings for her/himself and for communication with others. This third step is the real starting point of genuine mathematical thinking of the child (‘mathematising’).

From the perspective of the cultural-historical activity theory, we conceive of mathematising as a motivated cultural activity with specific tools and goal-oriented actions to solve problems that participants in this activity encounter. However, in our own observations in primary schools, we discovered that the goals for the use of mathematical tools (like measuring, adding, subtracting, etc.) could be of different kinds: first children used mathematical tools for solving problems in the context of everyday settings and cultural practices (like: finding out how much to pay in the shoe shop, or determining number of blocks one needs for building a wall around a castle). We can call this extra-mathematical use of tools. On the other hand, when growing older the children sometimes also become interested in the structure of the mathematical tools and the operations themselves, and start using the tools they have acquired for solving problems of the activity of mathematising itself, like 10 year old children who explored the structure of the number line and discovering (with the help of the teacher) even and uneven, the features of ‘10’, or even what happens when we go endlessly to the left on the number line and arrive ‘under zero’? We call these intramathematical reasoning. For young children (until eight), however, we never witnessed spontaneous intramathematical reasoning in the classroom. Their involvement with mathematics was only extramathematical: the use of mathematical tools for exploring concrete situations and for the achievement of practical goals in the cultural activities they play. This is the type of activity I will focus on in this article.

From these general theoretical assumptions about the enculturation of children in school, I have studied with my colleagues from the Vrije Universiteit Amsterdam (VU University Amsterdam) the development of cultural abilities like literacy and mathematising from preschool on. In this article I will review some outcomes of our research program on the development of mathematical thinking in 4–8 years old children over the past decades. This research program promotes research that is at the same time essentially theory-driven, evidence-based, and practically implemented. Methodologically, this means that we are not satisfied with positive empirical evidence alone, but also examine how this empirical result can be conceptually explained in terms of our CHAT theoretical framework, and how this outcome can be implemented by teachers in their everyday classroom. Hence, an important part of this research is accomplished in collaboration with teachers in their classrooms as long term quasi-experimental research or case-studies. The implementation process is most of the time also guided by teacher trainers who are expert in the (theoretical background of) Developmental Education (van Oers, 2012a, 2013a; van Oers & Pompert, 2021).

Productive Conditions

Over the past decades, we have discovered and researched a number of conditions that have turned out to be productive in promoting some form of mathematical thinking in young children. Such productive conditions (both interactional and situational) are assumed to be effective for the promotion of mathematical thinking, as they call for specific actions or imply affordances for such actions. From the CHAT perspective on human practical, perceptual, verbal and mental actions, we assume that all these actions are object-oriented, goal-directed and tool-based. This latter implies that all mathematical actions require the use of symbols (tools) that can be used to discover (intramathematical or extramathematical) new knowledge of a situation or – more often than not – the use of the operations that can be carried out on these symbols. The organized system of mathematical actions is called a mathematical activity, or just ‘mathematising’ (using a term from Freudenthal, 1973, p. 134). In an earlier overview of our research on young children’s mathematical activity (van Oers, 2014Footnote 1), I circumscribed ‘mathematising’ as ‘the activity of producing structured objects that allow further elaborations in mathematical terms through problem solving and (collective) reasoning/argumentation’ (van Oers, 2014, p. 112). The relevant objects children find in their direct environment can be collections of things, situations, patterns of events, and the like. In the above-mentioned 2014-article, I also argued that mathematising is a complex cultural practice which can only be accessed by newcomers (like young children) when they are allowed to play it. In play, children know and want to follow some of the rules of this practice, children are involved participants (i.e., they participate on their own willful accord), and enjoy some degrees of freedom in the choice of object, rules and tools. An essential condition to safeguard the mathematical nature of the activity, is the co-participation of an adult or more knowledgeable peer in this activity, provided she/he does not disturb the qualities of play (rules, degrees of freedom, involvement) (van Oers, 2004, 2012b).

A seminal insight of Vygotskij is his conception of social origin of psychological functions (including mathematical thinking). Psychological functions show their social origin in the fact that they maintain their communicative function when they are verbalized, and explain to the Self or someone else what the thinker has in mind. But even when they are internalized, we may theoretically assume that this inner speech is preserved in moments of orientation and control or evaluation (see for example Vygotskij, 1982/1934). It was Gal’perin in particular who elaborated this idea in a cohesive argument and empirical research (see Gal’perin, 1969, 1976).

In our research program, the above described tenets turned out to be powerful ideas to lead our research. Van Houten et al. (2013) demonstrated a positive correlation between children’s narrative competence (as measured by a standardized test) and their abilities in early arithmetic. This correlation may be caused by intermediating factors like sociocultural background and cannot by itself be interpreted as proof for a causal relationship between arithmetic and narrative competence. Nevertheless, it strongly suggests that the ability to communicate coherently about aspects of a situation (including mathematics) is a core factor in both types of competences. In another study of mathematical thinking in young children in primary school, we could further support this assumption about the importance of communicating in the process of promoting mathematical thinking (van Oers, 2013b). Characteristically, this thinking is based on ‘connected discourse’ (Luria, 1969, p. 138ff). That is to say, according to Luria, it shows that coherence is linked to the actual speech situation, and is syntagmatic, i.e., combines different terms into a meaningful proposition (Luria, 1969). In different previous studies we found that children like to use drawings in their play and integrate these with symbols representing number or quantity(−change), often to make sure to others that their drawing communicates extra information about the drawing and the context of its use. The use of drawings (and schemes) combined with symbols contributes to a further mathematisation of young children’s language (van Oers, 2002). As a matter of fact, these studies convergently support the productive role of connected discourse for the formation of emergent mathematical thinking.

Pondering further on the idea of communicative activity as a way to promote coherent mathematical thinking in children, we also wondered whether the use of more structured communicative tools (like schemes) could further support young children’s thinking on mathematical objects, like number, quantity, addition or subtraction, spatial relations etc. For the study of this question, we guided teachers in early years classroom (5–6 year olds) to participate in children’s play activities and introduce useful schematic representations (schemes like ground plan, construction plan, diagram) that were recognized by the children as interesting and helpful for solving problems in their activities (see for instance, van Oers, 1994, 1996). In their shoe-shop in the classroom, children for example piled up different sizes of shoes and copied this contraption by drawing a kind of histogram (see Fig. 1a); the teacher also offered them a so-called “feet measuring thing” (see Fig. 1b), which was appreciated by the children as a handy thing to figure out the size of their and the teacher’s shoes. In our studies we always took care that the presented schemes made sense for the children, were linked to a current and meaningful activity of the children, and were integrated into their own speech.

Fig. 1
2 diagrams. A. It depicts a pile-up of different-sized shoe boxes. B. It displays 6 different-sized outlines of foot pads.

(a) histogram of shoe boxes, (b) “feet measuring thing”

Full size image

In one of our further studies on this topic we conducted a longitudinal, quasi-experimental study with a pretest-post-test control group design (N = 133). In a 5-year olds classroom the teachers provide different types of schemas that fitted in the current activities of the children’s play. During the whole year the children had a variety of schematizing experiences (reading schemes, construction schemes, action plans). In the next year these children started their first mathematics lessons and their scores on mathematics tests (Post-test and delayed post-test) were compared to a randomly chosen control group of the same age that took the same tests. Our experimental groups scored significantly better on post-tests (both for arithmetic and schematizing) than the control group which had not got any experience with schematizing (Poland, 2007; Poland & van Oers, 2007; Poland et al., 2009; van Oers & Poland, 2007). However, in a delayed test after one-and-a-half year the children’s scores on an arithmetic test were not significantly different anymore. Obviously, good arithmetic scores can also be achieved by drill and practice.

In sum, in a series of theoretically connected studies on children’s manifestations of acts that we as adults could identify as productive conditions that could be linked to the meaningful promotion of mathematical thinking in the context of children’s play: playful enactment of the use of numbers and quantities, the use of symbolic tools like schematic representations, narrative competence, presence of an helpful adult or more knowledgeable peers for learning how to communicate about number, quantity and change. However, most of the studies mentioned above were carried out in classrooms with young children in the age of 5–8. We now have reasons to assume that mathematical (co-)thinking starts earlier than at the age of 5 years (see for example Carruthers & Worthington, 2006; Worthington, 2021; Worthington & van Oers, 2017).

When and How Do We Start?

In the educational literature, it is an empirically well-established fact, that children spontaneously engage during everyday situations with symbols, patterns and objects that are generally recognized in our culture as mathematical, long before they enter formal schooling in arithmetic (McMullen et al., 2019; Ramani et al., 2015; Rathé et al., 2016a, b; Wijns et al., 2020). The children (4–5 years old) encounter these symbols, etc. in their cultural environments: on the streets (e.g., numbers on cars, busses), supermarket (price list), in the newspapers, picture books etc. Children notice these numbers without directions from adults (see Rathé et al., 2022).

Despite the empirical evidence for young children’s awareness of numerocity and numbers, a more detailed description of the course of this evolution from spontaneous use of notions of numerocity and number to number concepts and operations, remained unspecified. My basic hypothesis was that the previously described Vygotskian three step approach to the development of mathematical thinking may be applicable in the younger ages too. The first interest in exploring the tenability of this hypothesis was to figure out how adults could help younger children improving their communicative ability regarding numerosity, number and changes in this intellectual domain, without direct instructions and/or impairing the quality of children’s spontaneous play.

In our own research group, it was Maulfry Worthington (UK), who addressed this problem with a well-balanced series of studies into the emergence and development of young children’s personal mathematical inscriptions in the context of their spontaneous play. This work was rooted in the work that she did before in collaboration with Carruthers in the UK (see Carruthers & Worthington, 2005, 2006). In their collaborative previous work, these researchers aimed at discovering and describing the range of these mathematical marks from early play exploration to later written calculations. Worthington’s researchFootnote 2 consisted of longitudinal (1 year), ethnographic research in case-studies taken from the contexts of children’s homes and nursery classrooms, particularly formatted as pretend play (see Worthington, 2021). In these play contexts, she observed how these young children built up their ability to communicate about quantity and number and to construct the types of graphical means they used. Her data collection was based on interviews with children, teachers and parents, and on participatory observations. The analyses were mainly qualitative, but in some cases data could be categorized into different classes of graphical means which permitted quantitative analyses too (e.g., regarding the use of different types of symbolic representations – derived from the work of Pierce’s semiotic view, Buchler, 1995 – in different groups of children). All participating children were selected from a nursery school and were 3–4 years old. This school was located in a large multicultural city in the southwest of England.

Worthington’s research project yielded a number of very interesting findings. Without trying to be exhaustive, a few of them must be mentioned here as they fit perfectly well into the body of my present argument regarding the development of young children’s mathematical thinking. First of all, Worthington could identify many cases of children who attempted to communicate about numbers and counting in their play setting, like the boy who had constructed a parking place completely with tickets and prices on each ticket (40 p., 60 p. etc.). It also turned out that the numberings were not suggested or imposed by the teacher, but were clearly drawn from children’s ‘funds of knowledge’, built up spontaneously in their home contexts, the adult world of his parents, events in the outside world, observations of the teacher’s behavior in her daily classroom activities (see Worthington & van Oers, 2016, 2017). Furthermore, Worthington could identify different types of graphical means constructed by the children, at first using their own words, scribble marks, drawings, or even alphanumerical number-like signs copied from their environments. Later on, the children started using iconic (like wavy lines for written texts), indexical (like arrows), and symbolic means, like tallies or numbers (categories borrowed from Pierce), and a new category referring to culturally developed symbols (like numbers, diagrams, plans, etc.).

Finally, the symbols evolved into the culturally accepted mathematical symbols. The observations of the nursery children’s spontaneous play and communications about number revealed that their ability to read the intentions of abstract mathematical language and recognize the patterns of their combinations, was growing step by step with the help of the teacher (Worthington et al., 2019). By communicating about numbers and quantities, it also turned out that the communicative signs for the children actually represented ‘texts’ about number, i.e., things that they could tell about or explain in a coherent narrative about numbers.Footnote 3 More detailed analyses of the communications between the children and the teacher revealed another mechanism of utmost importance in this respect. When playing with the children, teachers often provided new symbols or proper forms of the signs and spontaneous symbolizations of the children, but they did so only when the children showed need for such signs and symbols. No direct instructions. In due time, the children adopted the suggestions of the teacher and used them to expand their own texts. Hence we can say that the children’s shared numerical notions were actually intertextual. Constructing such intertextuality with the children should be regarded as an essential dynamic element for the emergence of mathematical meanings in young children (Worthington et al., 2023). Adult supervision of these intertextual mathematical constructions (e.g., when using diagrams, graphs, or reflecting about number: ‘what can we legitimately say about number?’) was essential for the correct ways of linking symbols in propositions about mathematical objects (a quality correctly named ‘grammaticity’ by Worthington, 2021, p. 106ff). Adults’ supervision that doesn’t reduce the value of the parameters of children’s play (rule-based, free to some extent, and involvement), is an essential productive condition for the communication about numbers, numerosity, quantity, etc. for the development of mathematical thinking and the construction of mathematically acceptable topic-predicate structures.

Discussion and Prospect

How can we conceptually understand the above presented productive conditions? What are the psychological dynamics of these processes? The potentially seminal relationships between the emergence of mathematical thinking and children’s ways of communication and narration about number, has been discussed by several academics (Pimm, 1987; Krummheuer, 1997; Lorenz, 2012; Maier & Schweiger, 1999; Sfard, 2008). As Pimm (1987, p. 76) pointed out: ‘Part of learning mathematics is learning to speak like a mathematician’. A lot of theoretical argumentation and empirical evidence has been accumulated since then. However, it is still important nowadays to clarify how this understanding is to be implemented into everyday classrooms with young children.

In our own research program we have spent serious efforts in adding to this understanding of the development of mathematical thinking with the help of appropriate communicative tools. It is clear from our observations that each of the productive conditions mentioned (play format, schematizing, narrative competence, intertextuality, interaction with adults) engages children in communication about quantity, numbers, relationships, patterns of signs, representational processes. Such communications not only invite children to think again and reflect, encouraged by questions like ‘Are you sure?’ (van Oers, 1996), but also to build topics of joint attention (Tomasello, 1999), which can be enriched in the ongoing discourse by new predicates produced by the child’s own thinking or offered by peers and adults. So, like Vygotskij already pointed out in the last chapter of his Thinking and Speech (Vygotsky, 1982/1934), the construction of topic – predicate structures belongs to the core of conceptual thinking (see also van Oers, 2006 for further argumentation and examples). Communication (‘speech’) is to be considered an essential means for conveying and analyzing meanings, according to Vygotskij. With respect to mathematical thinking, this is consistent with Sfard’s (2008) conceptualization of mathematizing. In such collaborative (communicative) constructions of increasingly elaborated and more sophisticated mathematical topic – predicate – structures, (young) learners get involved in intertextual interactions in which they weave together their own texts and those of others, provided they make sense for the learning child.

This ought to be a basically playful endeavor that highlights the rules of the game, but also allows the player enough ‘degrees of freedom’ in his actions and choices for explorations of the meanings and of the (intramathematical or extramathematical) limitations of the (mathematical) rules. Like in the explorations of the number line when children examine what it means to go ‘under zero’; does this make sense?

The role of the teacher is essential here in order to guarantee the cultural relevance of the children’s inventions for the enrichment of the (mathematical) topic-predicate structures. It is important to realize that this does not prohibit the teacher to teach the children. However, this should always be embeddedteaching, embedded in the context of the children’s playful engagements with mathematics, trying to answer their own questions. All assistance of the teacher should be connected to the children’s questions and interests in the context of their playful mathematics.

How to implement these ideas into the classrooms? In our own work in schools in the Netherlands for the implementation of the educational concept of Developmental Education (van Oers, 2012a, c; Slob et al., 2022; van Oers & Duijkers, 2013) we have elaborated a play-based curriculum approach in collaboration with teachers, teacher trainers and researchers, which helps teachers to organize their classroom work in the context of playful sociocultural practices. In the context of such practices, children encounter different kinds of problems (including mathematical ones) that they can try to solve with the help of teachers and peers. In this implementation strategy the main focus is on the innovation of teachers’ thinking about curriculum and meaningful learning. In our research thus far we may legitimately draw the conclusion that teachers can indeed initiate and promote dialogical discourses with young children about events and phenomena in their daily life (van der Veen, 2017). From this perspective it is also plausible to assume that such dialogical discourses concerning mathematical topics in everyday practices can indeed promote mathematical thinking in the context of playful participation in varying sociocultural contexts. We have strong reasons to continue along this path in the future.