Builtin Types Viewed as Inductive Families

Abstract

State of the art optimisation passes for dependently typed languages can help erase the redundant information typical of invariant-rich data structures and programs. These automated processes do not dramatically change the structure of the data, even though more efficient representations could be available.

Using Quantitative Type Theory as implemented in Idris 2, we demonstrate how to define an invariant-rich, typechecking-time data structure packing an efficient runtime representation together with runtime irrelevant invariants. The compiler can then aggressively erase all such invariants during compilation.

Unlike other approaches, the complexity of the resulting representation is entirely predictable, we do not require both representations to have the same structure, and yet we are able to seamlessly program as if we were using the high-level structure.

1 Introduction

Dependently typed languages have empowered users to precisely describe their domain of discourse by using inductive families [13]. Programmers can bake crucial invariants directly into their definitions thus refining both their functions’ inputs and outputs. The constrained inputs allow them to only consider the relevant cases during pattern matching, while the refined outputs guarantee that client code can safely rely on the invariants being maintained. This programming style is dubbed ‘correct by construction’.

However, relying on inductive families can have a non-negligible runtime cost if the host language is compiling them naïvely. And even state of the art optimisation passes for dependently typed languages cannot make miracles: if the source code is not efficient, the executable will not be either.

A state of the art compiler will for instance successfully compile length-indexed lists to mere lists thus reducing the space complexity from quadratic to linear in the size of the list. But, confronted with a list of booleans whose length is statically known to be less than 64, it will fail to pack it into a single machine word thus spending linear space when constant would have sufficed.

In section 2, we will look at an optimisation example that highlights both the strengths and the limitations of the current state of the art when it comes to removing the runtime overheads potentially incurred by using inductive families.

In section 3 we will give a quick introduction to Quantitative Type Theory, the expressive language that grants programmers the ability to have both strong invariants and, reliably, a very efficient runtime representation.

In section 4 we will look at an inductive family that we use in a performance-critical way in the TypOS project [2] and whose compilation suffers from the limitations highlighted in section 2. Our current and unsatisfactory approach is to rely on the safe and convenient inductive family when experimenting in Agda and then replace it with an unsafe but vastly more efficient representation in our actual Haskell implementation.

Finally in section 5, we will study the actual implementation of our efficient and invariant-rich solution implemented in Idris 2. We will also demonstrate that we can recover almost all the conveniences of programming with inductive families thanks to smart constructors and views.

2 An Optimisation Example

The prototypical examples of the naïve compilation of inductive families being inefficient are probably the types of vectors ( ) and finite numbers ( ). Their interplay is demonstrated by the function. Let us study this example and how successive optimisation passes can, in this instance, get rid of the overhead introduced by using indexed families over plain data.

A vector is a length-indexed list. The type is parameterised by the type of values it stores and indexed over a natural number corresponding to its length. More concretely, its constructor builds an empty vector of size (i.e. zero), and its (pronounced ‘cons’) constructor combines a value of type (the head) and a subvector of size (the tail) to build a vector of size ( ) (i.e. successor of n).

The size is not explicitly bound in the type of . In Idris 2, this means that it is automatically generalised over in a prenex manner reminiscent of the handling of free type variables in languages in the ML family. This makes it an implicit argument of the constructor. Consequently, given that is a type of unary natural numbers, a naïve runtime representation of a ( ) would have a size quadratic in . A smarter representation with perfect sharing would still represent quite an overhead as observed by Brady, McBride, and McKinna [6].

A finite number is a number known to be strictly smaller than a given natural number. The type is indexed by said bound. Its constructor models and is bound by any non-zero bound, and its constructor takes a number bound by and returns its successor, bound by ( ). A naïve compilation would here also lead to a runtime representation suffering from a quadratic blowup.

This leads us to the definition of the function. Provided a vector of size and a finite number bound by this same , we can define a total function looking up the value stored at position in the vector. It is guaranteed to return a value. Note that we do not need to consider the case of the empty vector in the pattern matching clauses as all of the return types of the constructors force the index to be non-zero and, because the vector and the finite number talk about the same , having an empty vector would automatically imply having a value of type ( ) which is self-evidently impossible.

Thanks to our indexed family, we have gained the ability to define a function that cannot possibly fail, as well as the ability to only talk about the pattern matching clauses that make sense. This seemed to be at the cost of efficiency but luckily for us there has already been extensive work on erasure to automatically detect redundant data [6] or data that will not be used at runtime [22].

2.1 Optimising 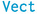, , and

An analysis in the style of Brady, McBride, and McKinna’s [6] can solve the quadratic blowup highlighted above by observing that the natural number a vector is indexed by is entirely determined by the spine of the vector. In particular, the length of the tail does not need to be stored as part of the constructor: it can be reconstructed as the predecessor of the length of the overall vector. As a consequence, a vector can be adequately represented at runtime by a pair of a natural number and a list. Similarly a bounded number can be adequately represented by a pair of natural numbers. Putting all of this together and remembering that the vector and the finite number share the same , can be compiled to a function taking two natural numbers and a list. In Idris 2 we would write the optimised as follows (we use the keyword because this transformed version is not total at that type).

We can see in the second clause that the recursive call is performed on the tail of the list (formerly vector) and so the first argument to corresponding to the vector’s size is decreased by one. The invariant, despite not being explicit anymore, is maintained.

A Tejiščák-style analysis [22] can additionally notice that the lookup function does not use the bound’s value and drop it. This leads to the lookup function on vectors being compiled to its partial-looking counterpart acting on lists.

Even though this is in our opinion a pretty compelling example of erasing away the apparent complexity introduced by inductive families, this approach has two drawbacks.

Firstly, it relies on the fact that the compiler can and will automatically perform these optimisations. But nothing in the type system prevents users from inadvertently using a value they thought would get erased, thus preventing the Tejiščák-style optimisation from firing. In performance-critical settings, users may rather want to state their intent explicitly and be kept to their word by the compiler in exchange for predictable and guaranteed optimisations.

Secondly, this approach is intrinsically limited to transformations that preserve the type’s overall structure: the runtime data structures are simpler but very similar still. We cannot expect much better than that. It is so far unrealistic to expect e.g. a change of representation to use a balanced binary tree instead of a list in order to get logarithmic lookups rather than linear ones.

2.2 No Magic Solution

Even if we are able to obtain a more compact representation of the inductive family at runtime through enough erasure, this does not guarantee runtime efficiency. As the Coq manual [11] reminds its users, extraction does not magically optimise away a user-defined quadratic multiplication algorithm when extracting unary natural numbers to an efficient machine representation. In a pragmatic move, Coq, Agda, and Idris 2 all have ad-hoc rules to replace convenient but inefficiently implemented numeric functions with asymptotically faster counterparts in the target language.

However this approach is not scalable: if we may be willing to extend our trusted core to a high quality library for unbounded integers, we do not want to replace our code only proven correct thanks to complex invariants with a wildly different untrusted counterpart purely for efficiency reasons.

In this paper we use Quantitative Type Theory [4, 16] as implemented in Idris 2 [5] to bridge the gap between an invariant-rich but inefficient representation based on an inductive family and an unsafe but efficient implementation using low-level primitives. Inductive families allow us to view [18, 24] the runtime relevant information encoded in the low-level and efficient representation as an information-rich compile time data structure. Moreover the quantity annotations guarantee the erasure of this additional information during compilation.

3 Some Key Features of Idris 2

Idris 2 implements Quantitative Type Theory, a Martin-Löf type theory enriched with a semiring of quantities classifying the ways in which values may be used. In a type, each binder is annotated with the quantity by which its argument must abide.

3.1 Quantities

A value may be runtime irrelevant, linear, or unrestricted.

Runtime irrelevant values ( quantity) cannot possibly influence control flow as they will be erased entirely during compilation. This forces the language to impose strong restrictions on pattern-matching over these values. Typical examples are types like the parameter in ( ), or indices like the natural number in ( ). These are guaranteed to be erased at compile time. The advantage over a Tejiščák-style analysis is that users can state their intent that an argument ought to be runtime irrelevant and the language will insist that it needs to be convinced it indeed is.

Linear values ( quantity) have to be used exactly once. Typical examples include the token used by Idris 2 to implement the monad à la Haskell, or file handles that cannot be discarded without first explicitly closing the file. At runtime these values can be updated destructively. We will not use linearity in this paper.

Last, unrestricted values (denoted by no quantity annotation) can flow into any position, be duplicated or thrown away. They are the usual immutable values of functional programming.

The most basic of examples mobilising both the runtime irrelevance and unrestricted quantities is the identity function.

Its type starts with a binder using curly braces. This means it introduces an implicit variable that does not need to be filled in by the user at call sites and will be reconstructed by unification. The variable it introduces is named and has type . It has the quantity annotation which means that this argument is runtime irrelevant and so will be erased during compilation.

The second binder uses parentheses. It introduces an explicit variable whose name is and whose type is the type that was just bound. It has no quantity annotation which means it will be an unrestricted variable.

Finally the return type is the type bound earlier. This is, as expected, a polymorphic function from to . It is implemented using a single clause that binds on the left-hand side and immediately returns it on the right-hand side.

If we were to try to annotate the binder for with a quantity to make it runtime irrelevant then Idris 2 would rightfully reject the definition. The following block shows part of the error message complaining that cannot be used at an unrestricted quantity on the right-hand side.

3.2 Proof Search

In Idris 2, Haskell-style ad-hoc polymorphism [25] is superseded by a more general proof search mechanism. Instead of having blessed notions of type classes, instances and constraints, the domain of any dependent function type can be marked as . This signals to the compiler that the corresponding argument will be an implicit argument and that it should not be reconstructed by unification alone but rather by proof search. The search algorithm will use the appropriate user-declared hints as well as the local variables in scope.

By default, a datatype’s constructors are always added to the database of hints. And so the following declaration brings into scope both an indexed family of proofs that a given boolean is , and a unique constructor that is automatically added as a hint.

As a consequence, we can for instance define a record type specifying what it means for to be an even number by storing its together with a proof that is both runtime irrelevant and filled in by proof search. Because ( ) computes to , Idris 2 is able to fill-in the missing proof in the definition of using the hint.

We will use both and the mechanism in section 5.3.

3.3 Application: , as

We can use the features of Quantitative Type Theory to give an implementation of that is guaranteed to erase to a at runtime independently of the optimisation passes implemented by the compiler. The advantage over the optimisation passes described in section 2 is that the user has control over the runtime representation and does not need to rely on these optimisations being deployed by the compiler.

The core idea is to make the slogan ‘a vector is a length-indexed list’ a reality by defining a record packing together the as a list and a proof its length is equal to the expected index. This proof is marked as runtime irrelevant to ensure that the list is the only thing remaining after compilation.

Smart constructors. Now that we have defined vectors, we can recover the usual building blocks for vectors by defining smart constructors, that is to say functions and that act as replacements for the inductive family’s data constructors.

The smart constructor returns an empty vector. It is, unsurprisingly, encoded as the empty list ( ). Because ( ) statically computes to , the proof that the encoding is valid can be discharged by reflexivity.

Using we can combine a head and a tail of size to obtain a vector of size ( ). The encoding is obtained by consing the head in front of the tail’s encoding and the proof this is valid ( ) uses the fact that propositional equality is a congruence and that ( ( )) computes to ( ( )).

View. Now that we know how to build vectors, we demonstrate that we can also take them apart using a view.

A view for a type T, in the sense of Wadler [24], and as refined by McBride and McKinna [18], is an inductive family V indexed by T together with a total function mapping every element t of T to a value of type (Vt). This simple gadget provides a powerful, user-extensible, generalisation of pattern-matching. Patterns are defined inductively as either a pattern variable, a forced term (i.e. an arbitrary expression that is determined by a constraint arising from another pattern), or a data constructor fully applied to subpatterns. In contrast, the return indices of an inductive family’s constructors can be arbitrary expressions.

In the case that interests us, the view allows us to emulate ‘matching’ on which of the two smart constructors or was used to build the vector being taken apart.

The inductive family is indexed by a vector and has two constructors corresponding to the two smart constructors. We use Idris 2’s overloading capabilities to give each of the ’s constructors the name of the smart constructor it corresponds to. By pattern-matching on a value of type ( ), we will be able to break into its constitutive parts and either observe it is equal to or recover its head and its tail.

The function demonstrates that we can always tell which constructor was used by inspecting the list. If it is empty, the vector was built using the smart constructor. If it is not then we got our hands on the head and the tail of the encoding and (modulo some re-wrapping of the tail) they are effectively the head and the tail that were combined using the smart constructor.

Application: We can then use these constructs to implement the function on vectors without ever having to explicitly manipulate the encoding. The maximally sugared version of is as follows:

On the left-hand side the view lets us seamlessly pattern-match on the input vector. Using the keyword we have locally modified the function definition so that it takes an extra argument, here the result of the intermediate computation ( ). Correspondingly, we have two clauses matching on this extra argument; the symbol separates the original left-hand side (here elided using because it is exactly the same as in the parent clause) from the additional pattern. This pattern can either have the shape or ( ) and, correspondingly, we learn that is either or ( ).

On the right-hand side the smart constructors let us build the output vector. Mapping a function over the empty vector yields the empty vector while mapping over a cons node yields a cons node whose head and tail have been modified.

This sugared version of is equivalent to the following more explicit one:

In the parent clause we have explicitly bound instead of merely introducing an alias for it by writing ( ) and so we will need to be explicit about the ways in which this pattern is refined in the two with-clauses.

In the with-clauses, we have explicitly repeated the refined version of the parent clause’s left-hand side. In particular we have used dotted patterns to insist that is now entirely forced by the match on the result of ( ).

We have seen that by matching on the result of the ( ) call, we get to ‘match’ on as if were an inductive type. This is the power of views.

Application: The type ( ) can similarly be represented by a single natural number and a runtime irrelevant proof that it is bound by . We leave these definitions out, and invite the curious reader to either attempt to implement them for themselves or look at the accompanying code.

Bringing these definitions together, we can define a function which is similar to the one defined in section 2.

We are seemingly using at two different types ( and respectively) but both occurrences actually refer to separate functions: Idris 2 lets us overload functions and performs type-directed disambiguation.

For pedagogical purposes, this sugared version of can also be expanded to a more explicit one that demonstrates the views’ power.

The main advantage of this definition is that, based on its type alone, we know that this function is guaranteed to be processing a list and a single natural number at runtime. This efficient runtime representation does not rely on the assumption that state of the art optimisation passes will be deployed.

We have seen some of Idris 2’s powerful features and how they can be leveraged to empower users to control the runtime representation of the inductive families they manipulate. This simple example only allowed us to reproduce the performance that could already be achieved by compilers deploying state of the art optimisation passes. In the following sections, we are going to see how we can use the same core ideas to compile an inductive family to a drastically different runtime representation while keeping good high-level ergonomics.

4 Thinnings, Cooked Two Ways

We experienced a major limitation of compilation of inductive families during our ongoing development of TypOS [2], a domain specific language to define concurrent typecheckers and elaborators. Core to this project is the definition of actors manipulating a generic notion of syntax with binding. Internally the terms of this syntax with binding are based on a co-de Bruijn representation (an encoding we will explain below) which relies heavily on thinnings. A thinning (also known as an Order Preserving Embedding [9]) between a source and a target scope is an order preserving injection of the smaller scope into the larger one. They are usually represented using an inductive family. The omnipresence of thinnings in the co-de Bruijn representation makes their runtime representation a performance critical matter.

Let us first remind the reader of the structure of abstract syntax trees in a named, a de Bruijn, and a co-de Bruijn representation. We will then discuss two representations of thinnings: a safe and convenient one as an inductive family, and an unsafe but efficient encoding as a pair of arbitrary precision integers.

4.1 Named, de Bruijn, and co-de Bruijn Syntaxes

In this section we will use the S combinator ($\lambda g. \lambda f. \lambda x. g x (f x)$) as a running example and represent terms using a syntax tree whose constructor nodes are circles and variable nodes are squares. To depict the S combinator we will only need $\lambda {}$-abstraction and application (rendered $) nodes. A constructor’s arguments become its children in the tree. The tree is laid out left-to-right and a constructor’s arguments are displayed top-to-bottom.

Named Syntax. The first representation is using explicit names. Each binder has an associated name and each variable node carries a name. A variable refers to the closest enclosing binder which happens to be using the same name.

To check whether two terms are structurally equivalent ($\alpha$-equivalence) potentially requires renaming bound names. In order to have a simple and cheap $\alpha$-equivalence check we can instead opt for a nameless representation.

De Bruijn Syntax. An abstract syntax tree based on de Bruijn indices [8] replaces names with natural numbers counting the number of binders separating a variable from its binding site. The S combinator is now written $(\lambda \, \lambda \, \lambda \, 2\, 0\, (1\, 0))$.

You can see in the following graphical depiction that $\lambda$-abstractions do not carry a name anymore and that variables are simply pointing to the binder that introduced them. We have left the squares empty but in practice the various coloured arrows would be represented by a natural number. For instance the one corresponds to 1 because you need to ignore one $\lambda {}$-abstraction (the one) on your way towards the root of the tree before you reach the corresponding magenta binder.

To check whether a subterm does not mention a given set of variables (a thickening test, the opposite of a thinning which extends the current scope with unused variables), you need to traverse the whole term. In order to have a simple cheap thickening test we can ensure that each subterms knows precisely what its support is and how it embeds in its parent’s.

Co-de Bruijn Syntax. In a co-de Bruijn representation [17] each subterm selects exactly the variables that stay in scope for that term, and so a variable constructor ultimately refers to the only variable still in scope by the time it is reached. This representation ensures that we know precisely what the scope of a given term currently is.

In the following graphical rendering, we represent thinnings as lists of full ($\bullet$) or empty ($\circ$) discs depending on whether the corresponding variable is either kept or discarded. For instance the thinning represented by throws the variable away, and keeps both the and ones.

We can see that in such a representation, each node in the tree stores one thinning per subterm. This will not be tractable unless we have an efficient representation of thinnings.

4.2 The Performance Challenges of co-de Bruijn

Using the co-de Bruijn approach, a term in an arbitrary context is represented by the pairing of a term in co-de Bruijn syntax with a thinning from its support into the wider scope. Having such a precise handle on each term’s support allows us to make operations such as thinning, substitution, unification, or common sub-expression elimination more efficient.

Thinning a term does not require us to traverse it anymore. Indeed, embedding a term in a wider context will not change its support and so we can simply compose the two thinnings while keeping the term the same.

Substitution can avoid traversing subterms that will not be changed. Indeed, it can now easily detect when the substitution’s domain does not intersect with the subterm’s support.

Unification requires performing thickening tests when we want to solve a metavariable declared in a given context with a terms seemingly living in a wider one. We once more do not need to traverse the term to perform this test, and can simply check whether the outer thinning can be thickened.

Common sub-expression elimination requires us to identify alpha-equivalent terms potentially living in different contexts. Using a de Bruijn representation, these can be syntactically different: a variable represented by the natural number v in $\varGamma$ would be $(1+v)$ in $\varGamma ,\sigma$ but $(2+v)$ in $\varGamma ,\tau ,\nu$. A co-de Bruijn representation, by discarding all the variables not in the support, guarantees that we can once more use syntactic equality to detect alpha-equivalence. This encoding is used for instance (albeit unknowingly) by Maziarz, Ellis, Lawrence, Fitzgibbon, and Peyton-Jones in their ‘Hashing modulo alpha-equivalence’ work [14].

For all of these reasons we have, as we mentioned earlier, opted for a co-de Bruijn representation in the implementation of TypOS [2]. And so it is crucial for performance that we have a compact representation of thinnings.

Thinnings in TypOS. We first carefully worked out the trickier parts of the implementation in Agda before porting the resulting code to Haskell. This process highlighted a glaring gap between on the one hand the experiments done using a strongly typed inductive representation of thinnings and on the other hand their more efficient but unsafe encoding in Haskell.

Agda. The Agda-based experiments use inductive families that make the key invariants explicit which helps tracking complex constraints and catches design flaws at typechecking time. The indices guarantee that we always transform the thinnings appropriately when we add or remove bound variables. In Idris 2, the inductive family representation of thinnings would be written:

The family is indexed by two scopes (represented as snoclists i.e. lists that are extended from the right, just like contexts in inference rules): the tighter scope and the wider one. The constructor corresponds to a thinning from the empty scope to itself ( is Idris 2 syntactic sugar for the empty snoclist), and and respectively extend a given thinning by keeping or dropping the most local variable ( is the ‘snoc’ constructor, a sort of flipped ‘cons’). The ‘name’ ( of type ) is marked with the quantity to ensure it is erased at compile time (cf. section 3).

During compilation, Idris 2 would erase the families’ indices as they are forced (in the sense of Brady, McBride, and McKinna [6]), and drop the constructor arguments marked as runtime irrelevant. The resulting inductive type would be the following simple data type.

At runtime this representation is therefore essentially a linked list of booleans ( being , and and respectively ( ) and ( )).

Haskell. The Haskell implementation uses this observation and picks a packed encoding of this list of booleans as a pair of integers. One integer represents the length of the list, and the other integer’s least significant bits encode the list as a bit pattern where is and is .

Basic operations on thinnings are implemented by explicitly manipulating individual bits. It is not indexed and thus all the invariant tracking has to be done by hand. This has led to numerous and hard to diagnose bugs.

Thinnings in Idris 2. Idris 2 is a self-hosting language whose core datatype is currently based on a well-scoped de Bruijn representation. This precise indexing of terms by their scope helped entirely eliminate a whole class of bugs that plagued Idris 1’s unification machinery.

If we were to switch to a co-de Bruijn representation for our core language we would want, and should be able, to have the best of both worlds: a safe and efficient representation!

Thankfully Idris 2 implements Quantitative Type Theory (QTT) which gives us a lot of control over what is to be runtime relevant and what is to be erased during compilation. This should allow us to insist on having a high-level interface that resembles an inductive family while ensuring that everything but a pair of integers is erased at compile time. We will exploit the key features of QTT presented in section 3 to have our cake and eat it.

5 An Efficient Invariant-Rich Representation

We can combine both approaches highlighted in section 4.2 by defining a record parameterised by a source ( ) and target ( ) scopes corresponding to the two ends of the thinnings, just like we would for the inductive family. This record packs two numbers and a runtime irrelevant proof.

Firstly, we have a natural number called corresponding to the size of the big end of the thinning ( ). We are happy to use a (unary) natural number here because we know that Idris 2 will compile it to an unbounded integer.

Secondly, we have an integer called corresponding to the thinning represented as a bit vector stating, for each variable, whether it is kept or dropped. We only care about the integer’s least significant bits and assume the rest is set to 0.

Thirdly, we have a runtime irrelevant proof that is indeed a valid encoding of size of a thinning from to . We will explore the definition of the relation later on in section 5.3.

The first sign that this definition is adequate is our ability to construct any valid thinning. We demonstrate it is the case by introducing functions that act as smart constructor analogues for the inductive family’s data constructors.

5.1 Smart Constructors for

The first and simplest one is , a function that packs a pair of (the size of the big end, and the empty encoding) together with a proof that it is an adequate encoding of the thinning from the empty scope to itself. In this instance, the proof is simply the constructor.

To implement both and , we are going to need to perform bit-level manipulations. These are made easy by Idris 2’s interface which provides us with functions to shift the bit patterns left or right ( , ), set or clear bits at specified positions ( , ), take bitwise logical operations like disjunction ( ) or conjunction ( ), etc.

In both and , we need to extend the encoding with an additional bit. For this purpose we introduce the function which takes a bit b and an existing encoding bs and returns the new encoding $bs\!\cdot {}\!b$.

No matter what the value of the new bit is, we start by shifting the encoding to the left to make space for it; this gives us which contains the bit pattern $bs\!\cdot {}\!0$. If the bit is then we need to additionally set the bit at position 0 to obtain $bs\!\cdot {}\!1$. Otherwise if the bit is , we can readily return the $bs\!\cdot {}\!0$ encoding obtained by left shifting. The correctness of this function is backed by two lemma: testing the bit at index 0 after consing amounts to returning the cons’d bit, and shifting the cons’d encoding to the right takes us back to the unextended encoding.

The smart constructor demonstrates that from a thinning from to and a runtime irrelevant variable we can compute a thinning from the extended source scope ( ) to the target scope ( ) where was kept.

The outer scope has grown by one variable and so we increment . The encoding is obtained by -ing the boolean to record the fact that this new variable is kept. Finally, we use the two lemmas shown above to convince Idris 2 the invariant has been maintained.

Similarly the function demonstrates that we can compute a thinning getting rid of the variable freshly added to the target scope.

We once again increment the , use to record that the variable is being discarded and use the lemmas ensuring its correctness to convince Idris 2 the invariant is maintained.

We can already deploy these smart constructors to implement functions producing thinnings. We use as our example. It is a filter-like function that returns a dependent pair containing the elements that satisfy a boolean predicate together with a proof that there is a thinning embedding them back into the input snoclist.

If the input snoclist is empty then the output shall also be, and builds a thinning from to itself. If it is not empty we can perform a recursive call on the tail of the snoclist and then depending on whether the predicates holds true of the head we can either or it.

We are now equipped with these smart constructors that allow us to seamlessly build thinnings. To recover the full expressive power of the inductive family, we also need to be able to take these thinnings apart. Let us now tackle this issue.

5.2 Pattern Matching on

The family is a sum type indexed by a thinning. It has one data constructor associated to each smart constructor and storing its arguments.

The accompanying function witnesses the fact that any thinning arises as one of these three cases.

We show the implementation of in its entirety but leave out the technical auxiliary lemma it invokes. The interested reader can find them in the accompanying material. We will however inspect the code compiles to after erasure in section 5.5 to confirm that these auxiliary definitions do not incur any additional runtime cost.

We first start by pattern matching on the of the thinning. If it is then we know the thinning has to be the empty thinning. Thanks to an inversion lemma called , we can collect a lot of equality proofs: the encoding has to be , the source and target scopes and have to be the empty snoclists, and the proof of the invariant has to be of a specific shape. Rewriting by these equalities changes the goal type enough for the typechecker to ultimately see that the thinning was constructed using the smart constructor and so we can use the view’s constructor.

In case the thinning is non-empty, we need to inspect the 0-th bit of the encoding to know whether it keeps or discards its most local variable. This is done by calling the function which takes a boolean and returns a value of type ( ( ) ( ( )) i.e. we not only inspect the boolean but also record which value we got in a proof using the family introduced in section 3.

If the bit is set then we know the variable is kept. And so we can invoke an inversion lemma that will once again provide us with a lot of equalities that we immediately deploy to reshape the goal’s type. This ultimately lets us assemble a sub-thinning and use the view’s constructor.

If the bit is not set then we learn that the thinning was constructed using . We can once again use an inversion lemma to rearrange the goal and finally invoke the view’s constructor.

We can readily use this function to implement pattern matching functions taking a thinning apart. We can for instance define , the function that counts the number of smart constructors used when manufacturing the input thinning and returns a proof that this is exactly the length of the source scope .

We proceed by calling the function on the input thinning which immediately tells us that we only have three cases to consider. The case is easily handled because the branch’s refined types inform us that both and are the empty snoclist whose length is evidently . In the branch we learn that has the shape ( ) and so we must return the successor of whatever the result of the recursive call gives us. Finally in the case, is untouched and so a simple recursive call suffices. Note that the function is correctly detected as total because the target scope is indeed getting structurally smaller at every single recursive call. It is runtime irrelevant but it can still be successfully used as a termination measure by the compiler.

5.3 The 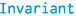Relation

We have shown the user-facing and have claimed that it is possible to define smart constructors , , and , as well as a function. This should become apparent once we show the actual definition of .

Definition of The relation maintains the invariant between the record’s fields (a ) and (an ) and the index scopes and . Its definition can favour ease-of-use of runtime efficiency because we statically know that all of the proofs will be erased during compilation.

As always, the constructor is the simplest. It states that the thinning of size and encoded as the bit pattern is the empty thinning.

The constructor guarantees that the thinning of size ( ) and encoding represents an injection from ( ) to ( ) provided that the bit at position of is set, and that the rest of the bit pattern (obtained by a right shift on ) is a valid thinning of size from to .

The constructor is structured the same way, except that it insists the bit at position should not be set.

We can readily use this relation to prove that some basic encoding are valid representations of useful thinnings.

Examples of proofs For instance, we can always define a thinning from the empty scope to an arbitrary scope .

The of this thinning is because every variable is being discarded and its is the length of the outer scope . The validity proof is provided by the lemma proven below. We once again use Idris 2’s overloading to give the same to functions that play similar roles but at different types.

The proof proceeds by induction over the outer scope . If it is empty, we can simply use the constructor for the empty thinning. Otherwise we can invoke on the induction hypothesis. This all typechecks because ( ) computes to and so the proof can be constructed automatically by Idris 2’s proof search (cf. section 3.2), and ( ) evaluates to which means the induction hypothesis has exactly the right type.

The definition of the identity thinning is a bit more involved. For a scope of size n, we are going to need to generate a bit pattern consisting of n ones. We define it in two steps. First, defines a bit pattern of k zeros followed by infinitely many ones by shifting k places to the left a bit pattern of ones only. Then, we obtain by taking the complement of .

We can then define the identity thinning for a scope of size n by pairing ( ) as the and as the .

The bulk of the work is once again in the eponymous lemma proving that this encoding is valid.

This proof proceeds once more by induction on the scope. If the scope is empty then once again the constructor for the empty thinning will do. In the non-empty case, we first appeal to an auxiliary lemma (not shown here) to construct a proof that the bit at position for a non-zero integer is known to be . We then need to use another lemma to cast the induction hypothesis which mentions ( ( )) so that it may be used in a position where we expect a proof talking about ( ( ( )) ).

Properties of the relation This relation has a lot of convenient properties.

First, it is proof irrelevant: any two proofs that the same , , , and are related are provably equal. Consequently, equality on values amounts to equality of the and values. In particular it is cheap to test whether a given thinning is the empty or the identity thinning.

Second, it can be inverted [12] knowing only two bits: whether the natural number is empty and what the value of the bit at position of the encoding is. This is what allowed us to efficiently implement the function by using these two checks and then inverting the proof to gain access to the proof that the remainder of the thinning’s encoding is valid. We will see in section 5.5 that this leads to efficient runtime code for the view.

5.4 Choose Your Own Abstraction Level

Access to both the high-level and the internal relation means that programmers can pick the level of abstraction at which they want to work. They may need to explicitly manipulate bits to implement key operators that are used in performance-critical paths but can also stay at the highest level for more negligible operations, or when proving runtime irrelevant properties.

In the previous section we saw simple examples of these bit manipulations when defining (using the constant 0 bit pattern) and using bit shifting and complement to form an initial segment of 1s followed by 0s.

Other natural examples include the meet and join of two thinnings sharing the same wider scope. The join can for instance be thought of either as a function defined by induction on the first thinning and case analysis on the second, emitting a constructor whenever either of the inputs does. Or we can observe that the bit pattern in the join is the disjunction of the inputs’ bit patterns and prove a lemma about the relation instead. This can be visualised as follows: in each column the meet is a $\bullet$ whenever either of the inputs is.

The join is of particular importance because it appears when we convert an ‘opened’ view of a term into its co-de Bruijn counterpart. As we mentioned earlier, co-de Bruijn terms in an arbitrary scope are represented by the pairing of a term indexed by its precise support with a thinning embedding this support back into the wider scope. When working with such a representation, it is convenient to have access to an ‘opened’ view where the outer thinning has been pushed inside therefore exposing the term’s top-level constructor, ready for case-analysis.

The following diagram shows the correspondence between an ‘opened’ application node using the view (the diamond ‘$’ node) with two subterms both living in the outer scope and its co-de Bruijn form (the circular ‘$’ node) with an outer thinning selecting the term support.

The outer thinning of the co-de Bruijn term is obtained precisely by computing the join of the respective outer thinnings of the ‘opened’ application’s function and argument.

These explicit bit manipulations will be preserved during compilation and thus deliver more efficient code.

5.5 Compiled Code

The following code block shows the JavaScript code that is produced when compiling the function. We chose to use the JavaScript backend rather than e.g. the ChezScheme one because it produces fairly readable code. We have modified the backend to also write comments reminding the reader of the type of the function being defined and the data constructors the natural number tags correspond to. These changes are now available to all in Idris 2 version 0.6.0.

The only manual modifications we have performed are the inlining of a function corresponding to a block, renaming variables and property names to make them human-readable, introducing the $tail definitions to make lines shorter, and slightly changing the layout.

Readers can see that the compilation process has erased all of the indices and the proofs showing that the invariant tying the efficient runtime representation to the high-level specification is maintained. A thinning is represented at runtime by a JavaScript object with two properties corresponding to ’s runtime relevant fields: and . Both are storing a JavaScript bigInt (one corresponding to the , the other to the ). For instance the thinning [01101] would be at runtime .

The view proceeds in two steps. First if the bigEnd is 0n then we know the thinning is empty and can immediately return the constructor. Otherwise we know the thinning to be non-empty and so we can compute the big end of its tail ($predBE) by subtracting one to the non-zero bigEnd. We can then inspect the bit at position 0 to decide whether to return a or a constructor. This is performed by using a bit mask to 0-out all the other bits ($th.bigEnd &1n) and checking whether the result is zero. If it is not equal to 0 then we emit and compute the $tail of the thinning by shifting the original encoding to drop the 0th bit. Otherwise we emit and compute the same tail.

By running on this [01101] thinning, we would get back ( [0110]), that is to say .

Thanks to Idris 2’s implementation of Quantitative Type Theory we have managed to manufacture a high level representation that can be manipulated like a classic inductive family using smart constructors and views without giving up an inch of control on its runtime representation.

The remaining issues such as the fact that we form the view’s constructors only to immediately take them apart thus creating needless allocations can be tackled by reusing Wadler’s analysis (section 12 of [24]).

6 Conclusion

We have seen that inductive families provide programmers with ways to root out bugs by enforcing strong invariants. Unfortunately these families can get in the way of producing performant code despite existing optimisation passes erasing redundant or runtime irrelevant data. This tension has led us to take advantage of Quantitative Type Theory in order to design a library combining the best of both worlds: the strong invariants and ease of use of inductive families together with the runtime performance of explicit bit manipulations.

6.1 Related Work

For historical and ergonomic reasons, idiomatic code in Coq tends to center programs written in a subset of the language quite close to OCaml and then prove properties about these programs in the runtime irrelevant Prop fragment. This can lead to awkward encodings when the unrefined inputs force the user to consider cases which ought to be impossible. Common coping strategies involve relaxing the types to insert a modicum of partiality e.g. returning an option type or taking an additional input to be used as the default return value. This approach completely misses the point of type-driven development. We benefit from having as much information as possible available during interactive editing. This information not only helps tremendously getting the definitions right by ensuring we always maintain vital invariants thus making invalid states unrepresentable, it also gives programmers access to type-driven tools and automation. Thankfully libraries such as Equations [20, 21] can help users write more dependently typed programs, by taking care of the complex encoding required in Coq. A view-based approach similar to ours but using Prop instead of the zero quantity ought to be possible. We expect that the views encoded this way in Coq will have an even worse computational behaviour given that Equations uses a sophisticated elaboration process to encode dependent pattern-matching into Gallina. However Coq does benefit from good automation support for unfolding lemmas, inversion principles, and rewriting by equalities. It may compensate for the awkwardness introduced by the encoding.

Prior work on erasure [22] has the advantage of offering a fully automated analysis of the code. The main inconvenience is that users cannot state explicitly that a piece of data ought to be runtime irrelevant and so they may end up inadvertently using it which would prevent its erasure. Quantitative Type Theory allows us users to explicitly choose what is and is not runtime relevant, with the quantity checker keeping us true to our word. This should ensure that the resulting program has a much more predictable complexity.

A somewhat related idea was explored by Brady, McKinna, and Hammond in the context of circuit design [7]. In their verification work they index an efficient representation (natural numbers as a list of bits) by its meaning as a unary natural number. All the operations are correct by construction as witnessed by the use of their unary counterparts acting as type-level specifications. In the end their algorithms still process the inductive family instead of working directly with binary numbers. This makes sense in their setting where they construct circuits and so are explicitly manipulating wires carrying bits. By contrast, in our motivating example we really want to get down to actual (unbounded) integers rather than linked lists of bits.

6.2 Limitations and Future Work

Overall we found this case study using Idris 2, a state of the art language based on Quantitative Type Theory, very encouraging. The language implementation is still experimental but none of the issues are intrinsic limitations. We hope to be able to push this line of work further, tackling the following limitations and exploring more advanced use cases.

Limitations. Unfortunately it is only propositionally true that ( ( )) computes to ( ) (and similarly for / and / ). This means that users may need to manually deploy these lemmas when proving the properties of functions defined by pattern matching on the result of calling the function. This annoyance would disappear if we had the ability to extend Idris 2’s reduction rules with user-proven equations as implemented in Agda and formally studied by Cockx, Tabareau, and Winterhalter [10].

In this paper’s case study, we were able to design the core relation making the invariants explicit in such a way that it would be provably proof irrelevant. This may not always be possible given the type theory currently implemented by Idris 2. Adding support for a proof-irrelevant sort of propositions (see e.g. Altenkirch, McBride, and Swierstra’s work [3]) could solve this issue once and for all.

The Idris 2 standard library thankfully gave us access to a polished pure interface to explicitly manipulate an integer’s bits. However these built-in operations came with no built-in properties whatsoever. And so we had to postulate a (minimal) set of axioms and prove a lot of useful corollaries ourselves. There is even less support for other low-level operations such as reading from a read-only array, or manipulating pointers.

We also found the use of runtime irrelevance (the quantity) sometimes frustrating. Pattern-matching on a runtime irrelevant value in a runtime relevant context is currently only possible if it is manifest for the compiler that the value could only arise using one of the family’s constructors. In non-trivial cases this is unfortunately only merely provable rather than self-evident. Consequently we are forced to jump through hoops to appease the quantity checker, and end up defining complex inversion lemmas to bypass these limitations. This could be solved by a mix of improvements to the typechecker and meta-programming using prior ideas on automating inversion [12, 15, 19].

Future work. We are planning to explore more memory-mapped representations equipped with a high level interface.

We already have experimental results demonstrating that we can use a read-only array as a runtime representation of a binary search tree. Search can be implemented as a proven-correct high level decision procedure that is seemingly recursively exploring the “tree”. At runtime however, this will effectively execute like a classic search by dichotomy over the array.

More generally, we expect that a lot of the work on programming on serialised data done in LoCal [23] thanks to specific support from the compiler can be done as-is in a QTT-based programming language. Indeed, QTT’s type system is powerful enough that tracking these invariants can be done purely in library code.

In the short term, we would like to design a small embedded domain specific language giving users the ability to more easily build and take apart products and sums efficiently represented in the style we presented here. Staging would help here to ensure that the use of the eDSL comes at no runtime cost. There are plans to add type-enforced staging to Idris 2, thus really making it the ideal host language for our project.

Our long term plan is to go beyond read-only data and look at imperative programs proven correct using separation logic and see how much of this after-the-facts reasoning can be brought back into the types to enable a high-level correct-by-construction programming style that behaves the same at runtime.