QCD and Supercomputers

Abstract

The title of this talk should rather have been Lattice QCD and Supercomputers. I will introduce Lattice QCD as the fundamental tool to predict (postdict) the hadron spectrum and most of the matrix elements relevant for hadronic physics in the non-perturbative regime. Lattice calculations are used to study the dynamics of QCD at large temperature or chemical potential, the anomalous magnetic moment of the muon, $g-$2, the nucleon structure functions, the meson scattering amplitudes at low and intermediate energies and, last but not least, the weak matrix elements relevant in flavour physics and CP violation. In this presentation only some example particularly illustrative of the present sophistication and accuracy of lattice QCD calculations will be discussed in some detail.

1 Introduction

In the last 40 years numerical simulations of Lattice QCD (LQCD) allowed an unpreceded progress in understanding the non-perturbative dynamics of strong interactions. Precise calculations of the hadron spectrum and accurate predictions of hadronic matrix elements are now a reality and more and more quantities relevant to the phenomenology of the Standard Model (SM) and for searches of signals of new physics beyond the SM (BSM) will soon become available. This progress has been possible thanks to the development of very sophisticated theoretical tools coupled to an extraordinary increase of the computer power and memory. In this talk a brief description of the methods of LQCD and of the main achievements obtained in recent years will be presented. The plan of this review is the following: after a general introduction, the derivation of the hadron spectrum and of the simplest matrix elements will be presented, followed by the description of the calculation of more complicated amplitudes such as those entering semi-leptonic decays or neutral meson mixing and non leptonic decays. Given the precision of the present calculations, radiative corrections and isospin breaking effects become relevant and they will also be discussed. A presentation of some anomalies in B decays which are difficult to be explained within the SM will then be given. The review is closed by an outlook on future developments.

2 Perturbative and Non-perturbative QCD

The QCD Lagrangian has indeed a very simple form

$$\begin{aligned} \mathcal{L}=-\frac{1}{2}Tr\left[ G_{\mu \nu }G^{\mu \nu }\right] +\sum _f\bar{q}_f ({\not \!\! D}-m_f)q_f+\theta \, Tr \left[ G_{\mu \nu }\tilde{G}^{\mu \nu }\right] \, , \end{aligned}$$

(10.1)

where $G_{\mu \nu }=G^A_{\mu \nu } t^A$ is the gluon tensor, $\tilde{G}^{\mu \nu }=\epsilon ^{\mu \nu \rho \sigma }G^A_{\rho \sigma } t^A$, $q_f$ are the quark fields and the last term represents the strong CP violating term which still waits for a satisfactory explanation. This term is related to a very interesting phenomenology but it will not be discussed in the following. Although the form of the Lagrangian is very simple, it gives rise to a very rich and complicated dynamics. In particular, because of asymptotic freedom [1, 2], the effective coupling decreases and quarks and gluons behave as almost free particles at large energies, see Fig. 10.1 [3]. In the high energy regime physical quantities can be computed in perturbation theory and the main limitations come from the order at which the amplitudes are computed and the accurary of the Montecarlos describing the hadronization processes for quark and gluons.

Fig. 10.1

The figures have been taken from [3]

Values of the strong coupling constant $\alpha _s(M^2_Z)=g_s^2(M^2_Z)/(4\pi )$ at the scale of the mass of the $Z^0$, left hand side, and $\alpha _s(Q^2)$ as a function of the scale, right hand side, from a wide set of experiments ranging from $\tau$ decays to jets at collider energies.

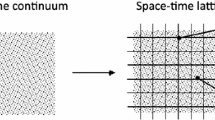
At low energy in order to study the dynamics of QCD, like the hadron spectrum or the weak matrix elements, a non-perturbative approach is necessary. Among all the possible methods the one which resulted the most reliable, with systematic effects that can be systematically reduced in time is QCD on the lattice, which consists in constructing the theory on a space-time that is a finite cubic lattice of points, which reduces to QCD when the mesh of the lattice is infinitely fine, that is the lattice spacing $a\rightarrow 0$, and simultaneously the physical volume goes to infinity, namely when the volume is much larger than the range of the interactions [4]. On a finite lattice, to describe ordinary matter, QCD requires more than 104 numbers for each lattice point, and this complexity explains why in LQCD it was necessary to reach an enormous computer power in order to be able to make realistic calculations, with small lattice spacings and physical volumes large enough. In the ’80s we started with computers with a power of one GigaFlops (1 GigaFlops $= 10^9$ operations/second) to arrive to the actual power of 0.1–1.0 Exaflops (1 ExaFlops $= 10^{18}$ operations/second) today ! A large part of this progress was due to the use of GPUs which were invented for video games [5, 6].

On the lattice all the physical information can be extracted from the Green functions of the theory, schematically

$$\begin{aligned} \langle 0 \vert \phi (x_1)\phi (x_2)\dots \phi (x_N)\vert 0 \rangle = \frac{1}{Z} \int \left[ d\phi \right] \phi (x_1)\phi (x_2)\dots \phi (x_N) \exp \left[ i S(\phi )\right] \, , \end{aligned}$$

(10.2)

where $Z=\int \left[ d\phi \right] \exp \left[ i S(\phi )\right]$ is a suitable normalisation factor and some regularisation must be introduced to make the expression in (10.2) finite. On a lattice with a finite number of lattice points ($L^4$) and a finite lattice spacing a, the functional integral in (10.2) becomes an integral on $L^4$ variables which can be performed using Important Sampling techniques, which require, however, the use of a mesh of points in an Euclidean space-time. Many of the present limitations in computing amplitudes with many particles in the final state derive from the unavoidable analytic continuation of the theory from the Minkowskian space-time to the Euclidean four-dimensional space.

Fig. 10.2

The figure is an updated version of the figure in [8] by G. Herdoiza

Values of the lightest pseudo-scalar mass, corresponding to the pion in the limit of physical quark masses, in LQCD simulations versus the physical volume, starting from the year 2001.

Let us consider now the calculation the simplest possible Green-function, namely the two point function

$$\begin{aligned} G(t,\vec q){=} \frac{1}{Z}\int d^3x \,\exp \left[ i \vec q \cdot \vec x\right] \,\langle 0 \vert \phi ^\dagger (t,\vec x)\phi (0,{\vec {0}}) \vert 0 \rangle = \sum _n \langle 0 \vert \phi ^\dagger \vert n \rangle \langle n\vert \phi \vert 0 \rangle \, \frac{e^{-E_n t}}{2E_n} \, ,\end{aligned}$$

(10.3)

where now the funtional integrals are all performed after a Wick rotation in the Euclidean space-time. At large time distances only the state with the smallest energy, $\vert E_\textrm{min}\rangle$, will contribute to $G(t,\vec q)$ and we may thus extract the energy of this state and the matrix element of the operator $\phi$, $\langle E_\textrm{min}\vert \phi \vert 0 \rangle$

$$\begin{aligned} \lim _\mathrm{t \rightarrow \infty } G(t,\vec q) = \langle 0 \vert \phi ^\dagger \vert E_\textrm{min} \rangle \langle E_\textrm{min}\vert \phi \vert 0 \rangle \, \frac{e^{-E_\textrm{min} t}}{2E_\textrm{min}} \, . \end{aligned}$$

(10.4)

If we consider the case $\vec q=0$ and the four component of the axial current, $\phi =A_0=\bar{u} \gamma _0\gamma _5$, as interpolating operator, for example, we can extract the mass of the pion, $m_\pi$, and its decay constant $f_\pi$, $\langle \pi \vert A_\mu \vert 0 \rangle =i f_\pi p_\mu$. Indeed all the quantities are obtained in dimensionless units, namely in units of the lattice spacing, $M_\pi =m_\pi a$ and we have to fix the mass of a set of hadrons to determine the value of the lattice spacing in physical units (GeV$^{-1}$ or fermi) and the physical masses of the quarks. For a recent discussion see [7] and references therein. By changing the lattice coupling, and by readjusting the lattice bare quark masses, we can make the dimensionless correlations lengths, $\xi _H=1/M_H$, corresponding to the inverse dimensionless hadron masses, larger and larger thus converging to the continuum limit. In this limit the physical volume must remain large i.e. the number of lattice point must increase, thus requiring larger and larger computer resources. Only quite recently it became possible to work at light quark masses very close to the physical point with lattice volumes large enough to avoid finite volume effects, Fig. 10.2. The agreement of the most recent lattice calculations with the experimental hadron spectrum is impressive. The results of the pioneering work of the BMW collaboration [9, 10] which first reached a sufficient accuracy by including isospin and electromagnetic corrections are given in Fig. 10.3.

Fig. 10.3

Courtesy of L. Lellouch, after [9, 10]

Comparison of lattice calculations and experimental values for the masses of several hadrons with different spin and flavour quantum numbers.

In order to compute more complicate amplitudes, for example the matrix elements of the vector and axial vector currents entering weak hadronic decays, one generalizes the method used to compute the pseudo-scalar decay constants. Thus for example one can define suitable sources/sinks to create/annihilate pseudo-scalar mesons in analogy with the axial current mentioned above

$$\begin{aligned} B^\dagger (t_1,\vec p_B) = \sum _{\vec x} B^\dagger (t_1,\vec x) \, e^{-i \vec p_B \cdot \vec x}\, , \qquad \pi (t_2,\vec p_\pi ) = \sum _{\vec x} \pi (t_2,\vec x) \, e^{+i \vec p_\pi \cdot \vec x}\, , \end{aligned}$$

(10.5)

and study the 3-point function

$$\begin{aligned} \langle 0 \vert \pi (t_2,\vec p_\pi ) J_\mu ^\textrm{weak}(0)B^\dagger (t_1,\vec p_B)\vert 0 \rangle \rightarrow \left[ \frac{\langle 0 \vert \pi \vert \pi (\vec p_\pi )\rangle \langle B(\vec p_B)\vert B^\dagger \vert 0 \rangle }{2 E_B 2 E_\pi }\right] \langle \pi (\vec p_\pi )\vert J_\mu ^\textrm{weak}\vert B(\vec p_B)\rangle \, , \end{aligned}$$

(10.6)

in the limit $t_1 \rightarrow -\infty$ and $t_2 \rightarrow +\infty$. The source/sink matrix elements and energies can be extracted from the two-point functions, thus we easily obtain the weak current matrix element $\langle \pi (\vec p_\pi )\vert J_\mu ^\textrm{weak}\vert B(\vec p_B) \rangle$. A similar procedure can be used for the matrix elements of the four fermion operators of the weak Hamiltonian and also to study more complicated final states as for examples two-pion states below the inelastic threshold. More complicated 4-particles final states or two pions above the inelastic threshold cannot be studied yet because the theory for the analytical continuation from the Minkowski to the Euclidean space in a finite volume has not been developed yet for these cases. A quick summary of main weak amplitudes which are computed in LQCD and used for flavour phenomenology are shown in Figs. 10.4.

Fig. 10.4

A synthetic overview of the amplitudes which are most frequently computed for weak interaction phenomenology is displayed in these figures. Left panel: Leptonic, Semi-leptonic and Radiative decays (also for baryons and electromagnetic transitions not shown in the figure). Right Panel: Non-leptonic decays of Kaons, Neutral meson mixing of $B_q$ mesons (also neutral D meson and Kaon mixing not shown in the figure). LQCD computed also some long distance contributions to K and D neutral meson mixing and short distance contributions to $B\rightarrow K^{(*)} \ell ^+\ell ^-$ decays, not shown in the figure

3 Lattice QCD and Flavour Physics

It would be very interesting to describe all the possible quantities that have been computed in LQCD so far, from QCD at finite temperature to structure functions, from two nucleon states to $g-2$. For lack of time I will restrict in the following to a few selected examples taken from weak interactions.

Our starting point is the CKM matrix [11, 12] in the SM (first term on the left-hand-side):

$$\begin{aligned} \mathbf {V_{CKM}} = \left( \begin{array}{ccc} V_{ud} &{} V_{us} &{} V_{ub} \\ V_{cd} &{} V_{cs} &{} V_{cb} \\ V_{td} &{} V_{ts} &{} V_{tb} \\ \end{array} \right) , \qquad \mathbf {V^W_{CKM}} = \left( \begin{array}{ccc} 1- 1/2\lambda ^2 &{} \lambda &{} A \lambda ^3 (\rho -i \eta ) \\ -\lambda &{} 1- 1/2\lambda ^2 &{} A \lambda ^2 \\ A \lambda ^3 (1-\rho -i \eta ) &{} - A \lambda ^2 &{} 1 \\ \end{array} \right) +O(\lambda ^4), \lambda =\sin \theta _c \,, \end{aligned}$$

(10.7)

where $\theta _c$ is the Cabibbo angle. The absolute values of the matrix elements, $\vert V_{ij}\vert$, are mostly determined by studying leptonic and semi-leptonic decays whereas only one independent phase, related to $\eta$, controls CP violating effects, for example in $K^0\rightarrow \pi \pi$ or $B \rightarrow D^{(*)} K^{(*)}$ decays. From the observation that the CKM matrix $\mathbf {V_{CKM}}$ is very close to the identity, Wolfenstein [13] suggested to expand it in powers of the sine of the Cabibbo angle. That defines the parameters $\rho$ and $\eta$ ($\bar{\rho }=\rho (1-1/2\lambda ^2)$ and $\bar{\eta }=\eta (1-1/2\lambda ^2))$ which will be used in the following (second term on the right-hand-side of (10.7)). Other important quantities are the unitarity triangles that can be defined using the unitarity of the CKM matrix. From the phenomenological point of view, the most renown of these triangles, because its sites correspond to well measurable quantities, is the one defined from the product of the first and third columns of the CKM matrix

$$\begin{aligned} V_{ud}V^*_{ub}+V_{cd}V^*_{cb}+V_{td}V^*_{tb}\,. \end{aligned}$$

(10.8)

The position of the vertex of the triangle in the $\bar{\rho }-\bar{\eta }$ plane can be determined by combining the measurements of several processes, e.g. semi-leptonic decays of heavy mesons, $B^0$-$\bar{B}^0$ and $K^0$-$\bar{K}^0$ mixing, the asymmetry in $B_d \rightarrow J/\psi K^0$ decays and many others [14], see Fig. 10.5.

Fig. 10.5

Left panel: the Standard triangle of the Standard Model; Right panel: pedagogical representation of the Unitarity Triangle, normalised to $V_{cd}V^*_{cb}$, in the $\bar{\rho }-\bar{\eta }$ plane. Each measurement corresponds to a curve and in the SM all the curves should meet in a point corresponding to one of the vertices of the unitarity triangle. The curves become bands, due to the experimental and theoretical uncertainties, in the $\bar{\rho }-\bar{\eta }$ plane. The overlap of the different bands is the allowed SM region in this plane

In order to compare experimental measurements and theoretical predictions we need the hadronic matrix elements of the weak currents or of the local operators of the Fermi-like weak Hamiltonian, schematically

$$\begin{aligned} Q^\textrm{EXP} = V_{CKM} \langle F\vert \hat{O}\vert I\rangle \, .\end{aligned}$$

(10.9)

From the measurement $Q^\textrm{EXP}$ and the matrix element $\langle F\vert \hat{O}\vert I\rangle$ computed in LQCD simulations we can determine a given combination of CKM matrix elements denoted here as $V_{CKM}$. The high quality (small uncertainties) of the lattice calculations of the hadronic matrix elements $\langle F\vert \hat{O}\vert I\rangle$ is illustrated by the examples given in Table 10.1.

Table 10.1 Full lattice inputs. The values of the different quantities have been obtained by mediating the $N_f =2+ 1$ and $N_f = 2 + 1+1$ FLAG numbers [15]

Fig. 10.6

$\bar{\rho }-\bar{\eta }$ plane with the SM global fit results in various configurations. The black contours display the 68% and 95% probability regions selected by the given global fit

Beyond the SM, (10.9) generalizes into

$$\begin{aligned} Q^\textrm{EXP} = \sum _i C^i_{SM}(M_W,m_t,\alpha _s, V_{CKM}) \langle F\vert \hat{O}_i\vert I\rangle + \sum _{i^\prime } C^{i^\prime }_{BSM}(\tilde{m}_\beta ,\alpha _s) \langle F\vert \hat{O}_{i^\prime }\vert I\rangle \, .\end{aligned}$$

(10.10)

New physics effects can modify the value of the Wilson coefficients $C^i_{SM}(M_W,m_t,\alpha _s, V_{CKM})$ of the operators already present in the SM or generate the contributions of new operators $O_{i^\prime }$ which do not appear in the SM. In this game the calculation of the hadronic matrix elements from lattice QCD is essential and no other non-perturbative approach (QCD-sum rules, chiral Lagrangians etc.) can compete with LQCD.

In the SM, in the absence of theoretical and experimental uncertainties, all the curves, corresponding to different physical processes, should meet in a single point of the $\bar{\rho }-\bar{\eta }$ plane. With the uncertainties, instead, the curves become bands which should overlap in the same region, Fig. 10.5. The results of the latest UTfit analysis [14, 16] are given in Fig. 10.6. We observe the impressive agreement between a very large set of experimental measurents and the SM expectations. Possible new physics effects, if present, must be rather tiny and models of physics BSM must cope with these results.

Although the overall picture shows a very good agreement of the experimental measurements with the SM predictions, there remain a few quantities, called anomalies or tensions, for which important differences have been observed between the theoretical expectations and the data. Some of them have been related to a possible failure of the Lepton Flavour Universality (LFU) with respect to weak interactions. The most difficult to explain are the ratios of the branching fractions of the rare-decays $R_{K^{(*)}}=BR(B\rightarrow K^{(*)}\mu ^+\mu ^-) /BR(B\rightarrow K^{(*) } e^+e^-)$ which differ from the expected value of about one by at least 2.6 $\sigma$ [17,18,19]. For these processes the lattice is not yet in the position to make reliable predictions and I will not discuss them in the following. Other tensions are observed in the difference in the value of $\vert V_{cb}\vert$ as determined from exclusive [20,21,22,23,24,25,26,27] or inclusive [28,29,30] B meson semi-leptonic decays and in the ratios $R_{D^{(*)}}=BR(B\rightarrow D^{(*)}\tau \nu _\tau ) /BR(B\rightarrow D^{(*)} \ell \nu _\ell )$, where $\ell$ is one of the light leptons ($\mu$ or e) [34,35,36,37,38,39,40,41,42,43]. Finally we may consider the unitarity test

$$\begin{aligned} \vert V_{ud}\vert ^2+\vert V_{us}\vert ^2+\vert V_{ub}\vert ^2=1 \, .\end{aligned}$$

(10.11)

$\vert V_{ud}\vert ^2$ accounts for 95% of this sum and for this reason a precise determination of this CKM matrix element from $\beta$ decays is of fundamental importance. Moreover, since the contribution from $\vert V_{ub}\vert ^2$ is very small, it is also very important, besides $\vert V_{ud}\vert ^2$, an accurate determination of $\vert V_{us}\vert ^2$ using LQCD. It turns out that there are strong hints that the currently accepted data for $\vert V_{ud}\vert$ and $\vert V_{us}\vert$ fall short of unitarity by 2$\sigma$ or even more, although a definite conclusion is still out of reach. One of the missing ingredients is a better control of the radiative electromagnetic corrections in $\beta$ decays. A accurate calculation of these corrections in LQCD is for this reason of the utmost importance. For both $B\rightarrow D^{(*)}$ semi-leptonic decays and the radiative corrections in weak decays the lattice will certainly play the role of protagonist in the near future and, for this reason, I will discuss these two cases in the following.

4 The Inclusive-Exclusive $V_{cb}$ Saga

Semi-leptonic B decays are very challenging processes from a phenomenological point of view because of two issues. The first one is the so-called $\vert V_{cb}\vert$ puzzle, namely the observation of a tension between the exclusive  [20,21,22,23,24,25,26,27] and the inclusive [28,29,30] determination of $\vert V_{cb}\vert$ at the level of 3.3 standard deviations. The second one is the discrepancy between the Standard Model predictions and experiments in the determinations of the $\tau /(\mu ,e)$ ratios of the branching fractions, the so called $R(D^{(*)})$ anomalies, which represent an important test of Lepton Flavour Universality (LFU). Some important novelties have, however, recently changed the previous situation: on the one hand the inclusive predictions were recently reconsidered and the uncertainties of the calculation performed in the Heavy Quark Effective Theory were reevaluated [31, 32]. On the other hand, new lattice calculations of the relevant form factors in the small recoil region [33], new approaches to their determination in the full kinematical range [44,45,46,47,48] and new measurements of the exclusive differential decay rates appeared. We think that it is possible to argue that for $\vert V_{cb}\vert$, although some difference remains, the tension is finally resolved, see the recent average from [47] given in (10.15) below. In the case of the value of $\vert V_{ub}\vert$ a difference between the inclusive and exclusive determinations at the 1.7 $\sigma$ still persists, although with large relative errors. A set of values from different estimates of $\vert V_{cb}\vert$ from inclusive and exclusive decays are given in Table 10.2. Note that all the form factors relevant to determine $\vert V_{cb}\vert$ from exclusive decays have been computed in lattice QCD.

Table 10.2 Values of $\vert V_{cb}\vert$ from inclusive or exclusive determinations. $^a$ This value of $\vert V_{cb}\vert \times 10^3$ has been derived using the value of the form factor at zero recoil given in (267) of [15]. DM in the rows 2-4-5-11 denotes the values obtained by using the Dispersive Matrix approach mentioned in the text

4.1 The Classical Determination of $\vert V_{cb}\vert$

For $B \rightarrow D^*$ semi-leptonic decays, one averages the form factor F(1) obtained from $N_f=2+1$, $F(1)=0.906(13)$, and $N_f=2+1+1$, $F(1)=0.895(10)(24)$ [15], obtaining $F(1)=0.904(11)$; then, using the formula derived from the rate, $F(1)\, \eta _{EW} \, \vert V_{cb}\vert = 35.44 (64) 10^{-3}$, and $\eta _{EW} = 1.00662$ one gets $\vert V_{cb}\vert = 38.95 (86) 10^{-3}$; for $B\rightarrow D$, following [15], the result is $\vert V_{cb}\vert = 40.0(1.0) 10^{-3}$.

Averaging the above values of $\vert V_{cb}\vert$ from $B \rightarrow D^*$ and $B \rightarrow D$ one obtains

$$\begin{aligned} \vert V_{cb}\vert \cdot 10^3 \, \, \, \mathrm{(excl.)} = 39.44 (65)\, . \end{aligned}$$

(10.12)

This procedure uses all the available information from $B \rightarrow D^*$ but neglects the correlation of the lattice determination of form factors for $B \rightarrow D^*$ and $B \rightarrow D$ decays obtained using the same gauge field configurations. Taking into account the correlation of the lattice determination of form factors for these decays, the final result is

$$\begin{aligned} \vert V_{cb}\vert \cdot 10^3 \, \, \, \mathrm{(excl.)} = 39.44 (63)\, , \end{aligned}$$

(10.13)

which differs by 3.3 $\sigma$ from the inclusive value in Table 10.2. We may combine the inclusive value of $\vert V_{cb}\vert$ in Table 10.2 with the result in (10.13) obtaining

$$\begin{aligned} \vert V_{cb}\vert \cdot 10^3 \, \, \, = 41.1 (1.3) \, \, \, \mathrm{(incl.+excl.)}\, . \end{aligned}$$

(10.14)

4.2 The Dispersive Matrix Determination

An alternative determination of the exclusive value of $\vert V_{cb}\vert$ can be obtained by using the values obtained using the Dispersive Matrix (DM) approach of [44] and given in Table 10.2, [46,47,48]. Besides the use of the DM approach, in the analysis of $B \rightarrow D^{(*)}$ decays it was essential a critical reappraisal of the experimental differential distributions and correlations among data and of the difference between the slope of $d\Gamma /dq^2$, where $q^2$ is the momentum transfer, between the lattice calculations and the experimental data. By combining these results, which include $B_s \rightarrow D^{(*)}_s$ decays, the exclusive value was

$$\begin{aligned} \vert V_{cb}\vert \cdot 10^3 \, \, \, \mathrm{(DM \,\,\, excl.)} = 41.2 (8)\, , \end{aligned}$$

(10.15)

namely a value much closer and compatible at the 1 $\sigma$ level with the inclusive one, with an uncertainty comparable to the uncertainty quoted in (10.13) . By combining the inclusive value of Table 10.2 with the DM result in (10.15) one obtains the (more precise) result

$$\begin{aligned} \vert V_{cb}\vert \cdot 10^3 \, \, \, = 41.9 (4) \mathrm{(incl.+excl.-DM)}\, . \end{aligned}$$

(10.16)

4.2.1 $\vert V_{ub}\vert$

The matrix element $V_{ub}$ is determined from the measurements of the branching ratios of leptonic $B \rightarrow \tau \nu _\tau$ decays, using the lattice determination of the B meson decay constant $f_B$, and from exclusive and inclusive semi-leptonic $b \rightarrow u$ decays. Its precision is limited by the uncertainty of the theoretical calculations of the B meson decay constant and of the relevant form factors, for leptonic and exclusive semi-leptonic decays, and of the matrix elements of the operators appearing in the HQET expansion of the inclusive rate. For $B \rightarrow \tau \nu _\tau$, which is very interesting because it is particularly sensitive to physics beyond the SM, a further source of large uncertainty comes for the large error in the experimental measurement of the rate. Although the determinations from inclusive semi-leptonic decays are systematically higher than the exclusive ones, the two values are compatible, once the spread of the inclusive determinations using different theoretical models is considered.

For the exclusive semi-leptonic decays we take the lattice number of Table  57 of [15], quoted in b). Finally, for inclusive semi-leptonic decays we use the value b) in (10.17) from the same reference. We give the average of a) and b) in c).

$$\begin{aligned} V_{ub}^{B\rightarrow \pi }= & {} 3.74 (17) \cdot 10^{-3} \quad a) \nonumber \\ V_{ub}^\mathrm{incl.\,\,}= & {} 4.32 (29) \cdot 10^{-3} \quad b) \nonumber \\ V_{ub}^{a+b\,\,}= & {} 3.89 (25) \cdot 10^{-3} \quad c) \end{aligned}$$

(10.17)

A percent precision is expected to be reached by LQCD using Exaflops CPUs for $f_B$ and for the form factors entering the exclusive determination of $\vert V_{ub}\vert$. A higher precision will require the non-perturbative calculation of the radiative corrections to the decay rates [7]. The progress of lattice calculations allow us to use in the analysis also the constraint coming from the ratio $\vert V_{ub}\vert /\vert V_{cb}\vert$ determined either from $\Lambda _b \rightarrow (p,\Lambda _c) \mu ^-\bar{\nu }_\mu$ or $B_s\rightarrow (K^-,D_s^-)\mu ^+\nu _\mu$ decays. We use only the latter decays since the lattice form factors relevant in $\Lambda _b$ decays do not satisfy the quality criteria of FLAG [15]. Following  [15] we quote

$$\begin{aligned} \frac{\vert V_{ub}\vert }{\vert V_{cb}\vert } =0.0844(56) \, . \end{aligned}$$

(10.18)

We note here that the DM method for $\vert V_{ub}\vert$ [51] gives, within the errors, substantially the same result which have been reported in this subsection, namely $\vert V^\textrm{excl}_{ub}\vert =3.69(34)$.

4.3 $\vert V_{ub}\vert$, $\vert V_{cb}\vert$ and UTfit

The above numbers can be compared with the results of the Global UTfit analysis or with the values obtained by predicting the values of $V_{cb}$ and $V_{ub}$ by making the UTfit analysis without including at all semi-leptonic decays, denoted as UTfit Prediction [16]:

$$\begin{aligned} \textrm{Global} \, \text {SM} \, \text {Fit} \,\,\,\,&\qquad&\textrm{UTfit} \, \text {Prediction}\nonumber \\ \vert V_{cb}\vert \times 10^3 = 42.4 (0.4)&\qquad&\vert V_{cb}\vert \times 10^3 = 42.6 (0.5) \nonumber \\ \vert V_{ub}\vert \times 10^3 = 3.72(0.09)&\qquad&\vert V_{ub}\vert \times 10^3 = 3.70(0.10) \, . \end{aligned}$$

(10.19)

Fig. 10.7

The figures have been taken from  [16]

Comparison of experimental results and lattice predictions for $\vert V_{cb}\vert$-$\vert V_{ub}\vert$ (left panel) and R(D)-$R(D^*)$ (right-lower panel). In the case of $\vert V_{cb}\vert$-$\vert V_{ub}\vert$ the results of the global UTfit analysis is also displayed (right-upper panel).

The situation is illustrated in Fig. 10.7: on the left panel the input values of the classical determinations of $\vert V_{cb}\vert$ are shown together with $\vert V_{ub}\vert$, and the value of $\vert V_{ub}\vert /\vert V_{cb}\vert$ from $B_s \rightarrow K$ semi-leptonic decays. The ratio $\vert V_{ub}\vert /\vert V_{cb}\vert$ from $\Lambda _b$ decays has not been used because the lattice results do not satisfy the FLAG quality requests [15]. In this panel also the results of the global UTfit analysis are given, showing that the inclusive value of $\vert V_{cb}\vert$ and the exclusive value of $\vert V_{ub}\vert$ are preferred. On the right panel we compare the results in the $\vert V_{cb}\vert$-$\vert V_{ub}\vert$ plane with the values of the standard determination of these CKM matrix elements, the values obtained with the DM approach [44, 46, 48] and UTfit. The agreement between the DM results and the global UTfit analysis is remarkable. On the right panel we also compare the predictions for R(D) and $R(D^*)$ using the calssical approach and the DM results. In the latter case the tension between experimental results and the theoretical predictions is strongly reduced.

5 Radiative Corrections to Weak Decays

The precision in determining hadron masses and weak amplitudes is such that it is no more possible to ignore isospin breaking effects or radiative corrections, simply denoted in the following as isospin corrections. From Table 10.1 we see that the precision in the determination of $f_K/f_\pi$ is 0.16% and on the semi-leptonic form factor for $K \rightarrow \pi$ decays is about 0.18%, in both cases smaller than the size of the isospin corrections which are expected of the order of 1.0%. For this reason the Rome-Southampton group developed a strategy to include isospin corrections in the amplitudes/rates relevant to weak decays [7, 52,53,54,55,56,57]. The recent progress in this field gave also the possibility of studying decays of light or heavy hadrons accompanied by the emission of a real photon or a virtual photon of mass $q^2$ that then materialises as a lepton pairs in the final state [55,56,57]. In this section we discuss the present status of the calculation of radiative corrections to weak decays in LQCD.

Let us start from the inclusive decay rate of a pseudo-scalar photon. The formula which includes isopin breaking and radiative corrections can be written as

$$\begin{aligned} \Gamma (P^+\rightarrow \ell ^+\nu _\ell +(\gamma )) =\frac{G_F^2}{8\pi } \vert V_{q_1q_2}\vert ^2 m_\ell ^2 m_P \, \left( 1-\frac{m_\ell ^2}{m_P^2}\right) ^2 f_P^2 S_\textrm{ew} \left( 1+\delta R^P_{IB}+\delta R^P_\textrm{QED}\right) \, , \end{aligned}$$

(10.20)

where $f_P$ is the leptonic decay constant in isoQCD ($m_u=m_d$, $e_f=0$); $R^P_{IB}$ are the strong isospin breaking corrections $\propto (m_u-m_d)/\Lambda _\textrm{QCD} \sim O(1\%)$; $R^P_\textrm{QED}$ are the QED corrections $\propto \alpha _\textrm{em} \sim O(1\%)$. Note that, at order $\alpha _\textrm{em}$, the separation between $R^P_\textrm{IB}$ and $R^P_\textrm{QED}$ is artificial and depends on the convention. In the calculation of $\Gamma$ the problem is the appearence, in the intermediate steps of the calculation, of infrared divergences in the zero-photon, $\Gamma _0$, or one-photon, $\Gamma _1$, emission rates at $O(\alpha _\textrm{em} )$. The combination of the two, however, is infrared finite and a strategy to regularise the infrared divergences in the intermediate steps has been developed by the Rome-Southampton Collaboration. The result has been used to compute the correction to the ratio $\Gamma (K^-\rightarrow \mu ^- \bar{\nu }_\mu +(\gamma ))/\Gamma (\pi ^-\rightarrow \mu ^- \bar{\nu }_\mu +(\gamma ))$ and extract the most precise value of $\vert V_{us}\vert /\vert V_{ud}\vert$, namely

$$\begin{aligned} \frac{\vert V_{us}\vert }{\vert V_{ud}\vert } =0.23134(24)_\textrm{exp}(30)_\textrm{th} = 0.23134(38)\, , \end{aligned}$$

(10.21)

which, using $\vert V_{ud}\vert$ from nuclear decays, corresponds to $\vert V_{us}\vert =0.2254(4)$. With the latest values and reevaluation of the uncertainties due to radiative corrections to $\beta$-decays [58,59,60,61,62], i.e. to $\vert V_{ud}\vert =0.97373(31)$, the most updated number is now $\vert V_{us}\vert =0.2251(8)$.

We have seen that the decays of charged pseudo-scalar mesons into light leptons, $P\rightarrow \ell \nu _\ell \gamma$ represent an important contribution to flavour physics since they give access to the CKM matrix elements  [11, 12]. At tree level, i.e. without a photon in the final state, these decays are helicity suppressed in the SM due to the V -A structure of the leptonic weak charged current, while the helicity suppression can be overcome by the radiated photons. Therefore, radiative leptonic decays may provide sensitive probes of possible SM extensions inducing non-standard currents and/or non-universal corrections to the lepton couplings. Radiative leptonic decays also provide a powerful tool with which to investigate the internal structure of the decaying meson. In addition to the leptonic decay constant $f_P$, there are indeed two other structure-dependent (SD) amplitudes describing the emission of real photons from hadronic states, usually parametrized in terms of the vector and axial-vector form factors, FV and FA respectively. Thus, a first-principle calculation of radiative leptonic decays requires a non-perturbative accuracy, which can be provided by numerical QCD+QED simulations on the lattice.

In [56] a comparison between the theoretical predictions based on the non-perturbative determination of the SD form factors FV and FA and the experimental data available on the leptonic radiative decay $K \rightarrow e \nu _e \gamma$ from the KLOE Collaboration [63], on the decay $K \rightarrow \mu \nu _\mu \gamma$ from E787 [64], ISTRA+  [65] and OKA [66] collaborations and on the decay $\pi ^+\rightarrow e^+\nu _e\gamma$ from the PIBETA Collaboration [67] was presented. An example of the comparison of the lattice prediction with the KLOE measurements is given in Fig. 10.8. There is good consistency between the theoretical predictions and the experimental results from the KLOE experiment on $K \rightarrow e \nu _e \gamma$ decays [63], but a discrepancy at the level of about 2 standard deviations for the data at large $x_\gamma$ from the E787 experiment on $K \rightarrow \mu \nu _\mu \gamma$ decays. $x_\gamma =2 P\cdot /m_P^2$ where P is the four-momentum of the decaying meson with mass $m_P$ and k is the four-momentum of the photon. Indeed the results from the two experiments do not agree. There are differences of up to 3–4 standard deviations at large photon energies in the comparison of the predictions with the E787, ISTRA+ and OKA data on radiative kaon decays as well as for some kinematical regions of the PIBETA experiment on the radiative pion decay. These conclusions call for improvements in the determination of the structure-dependent form factors $F^+(x_\gamma )$ and $F^-(x_\gamma )$ from both experiment and theory (for a definition of the different form factors see [56]).

Fig. 10.8

Left panel: comparison of the KLOE experimental data $\Delta R^\textrm{exp,i}$ [63] (red circles) with the theoretical predictions $\Delta R^\textrm{th,i}$ (blue squares) evaluated with the vector and axial form factors of [56]. The green diamonds correspond to the prediction of ChPT at order $O(e^2p^4)$. Right panel: Comparison of the form-factor $F ^+(x_\gamma )$ extracted by the KLOE collaboration in [63] and the theoretical prediction from lattice QCD [56]. The shaded areas represent uncertainties at the level of 1 standard deviation

The study of radiative decays with both real and virtual photons open the road to predict, and compare with experiments, many rare-decay rates, with the possibility of putting interesting bounds on physics BSM, for example in $B\rightarrow \mu ^+\mu ^-\gamma$ decays. It also give us the possibility of computing the radiative corrections to the neutron $\beta$ decay, the Holy Grail of these kind of calculations.

6 Conclusions

Thanks to the impressive development of computer resources and to the progress in the theoretical methods, Lattice QCD is now in the position of providing very accurate and reliable predictions for a large variety of hadronic quantities and of giving the possibility to detect even smallish effects of physics beyond the Standard Model. We have described in more detail two cases, $B\rightarrow D^{(*)}$ semi-leptonic decays and radiative corrections, where the precision of the theoretical predictions has sensibly improved in the recent past and shown the phenomenological implications of this improvements. More results on the anomalous magnetic moment of the muon, inclusive processes, axion physics and weak interaction are foreseen in the near future.