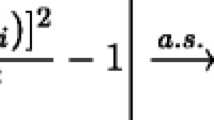Abstract
Classification of time series signals has become an important construct and has many practical applications. With existing classifiers, we may be able to classify signals accurately; however, that accuracy may decline if using a reduced number of attributes. Transforming the data and then undertaking a dimensionality reduction may improve the quality of the data analysis, decrease the time required for classification and simplify models. We propose an approach, which chooses suitable wavelets to transform the data, then combines the output from these transformations to construct a dataset by applying ensemble classifiers. We demonstrate this on different data sets across different classifiers and use different evaluation methods. Our experimental results demonstrate the effectiveness of the proposed technique, compared to the approaches that use either raw signal data or a single wavelet transform.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Noise here includes missing or misclassification of values as well as other induced random fluctuations in the data.
- 2.
We designate these signals as raw or unmodified Data.
- 3.
note: \(\sum ^J_{j=1} \frac{n}{2^j} = \frac{n}{2} + \frac{n}{4} + \dots + 2 + 1 = 2^J -1 = n-1\).
- 4.
Decomposing \(X_t: n=2^J\), to level \(J_0 : 1 \le J_0 \le J\) then \({\textbf {V}}_{J_0}\) has \(n/2^{J_0}\) elements.
- 5.
Which permits construction of a plot of cumulative energy% in the signal (or representation of), against the number of data points, see Fig. 2.
- 6.
As the DWT is an orthonormal transform, the energy in the transform (consisting of all \(J + 1\) subvectors) equates to the energy in the signal.
- 7.
We also applied single Decision tree classifiers to the MDWT data as a baseline to compare with ensemble classifiers.
- 8.
Smoothness defined here as: standard deviation of the of first differences of a time series elements. i.e. standard deviation of (\(X_S\)) : \(X_S = x_1 - x_2, x_2 - x_3, \ldots , x_{n-1} - x_n \).
- 9.
For the Ensemble Classifiers* throughout our experiment we set number of trees used to 100, no fine tuning of parameters was undertaken.
- 10.
In this instance we also include the Extra coefficients as they represent considerable signal energy.
- 11.
Using Accuracy % here is a suitable metric, as the dataset is reasonably balanced i.e. Class 1 has 81 records, Class 2 and 3 have 65 records each.
- 12.
As indicated by the NPES, Fig. 2.
- 13.
The average energy/information provided by the Extra coefficients at level \(\mathcal {S}_3\), per transformed signal is only 0.5% hence little if at all any gain in accuracy is achieved by including the Extra coefficients at this level.
References
Clark, P., Niblett, T.: Induction in noisy domains. In: Progress in Machine Learning (from the Proceedings of the 2nd European Working Session on Learning), 11–30, Bled, Sigma Press, Yugoslavia (1987)
Li, D., Bissyand’e, T., Klein, J., Le Traon, Y.: Time series classification with discrete wavelet transformed data: insights from an empirical study. In: The 28th International Conference on Software Engineering and Knowledge Engineering (2016)
Fong, S.: Using hierarchical time series clustering algorithm and wavelet classifier for biometric voice classification. J. Biomed. Biotechnol. 2012, Article ID 215019 (2012)
Grimaldi, M., Kokaram, A., Cunningham, P.: Classifying music by genre using wavelet packet transform and a round-robin ensemble. Comp Science Dept.; Electronic and Electrical Engineering Dept, Trinity College Dublin, Ireland (2002)
Grant, P., Islam, M.Z.: A novel approach for noisy signal classification through the use of multiple wavelets and ensembles of classifiers. In: Li, J., Wang, S., Qin, S., Li, X., Wang, S. (eds.) ADMA 2019. LNCS (LNAI), vol. 11888, pp. 195–203. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-35231-8_14
Moazami-Goudarzi, M., Moradi, Md. H., Abbasabadi, S.: High performance method for electrocardiogram compression using two dimensional multiwavelet transform. In: IEEE 7th Workshop on Multimedia Signal Processing (2006)
Graps, A.: An Introduction to wavelets. IEEE Comput. Sci. Eng. Sum. 2(2), 50–61 (1995)
Percival, D.B., Walden, A.T.: Wavelet Methods for Time Series Analysis, Cambridge University Press, New York (2000)
Nason, G.P.: Wavelet Methods in Statistics with R. Springer, New York. (2008). https://doi.org/10.1007/978-0-387-75961-6
R Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria (2013). https://www.r-project.org
Constantine, W., Percival, D.: WMTSA: Wavelet Methods for Time Series Analysis. R package version 2.0-3 (2017)
Frank, E., Hall, M.A., Witten I.H.: The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques, 4th edn. Morgan Kaufmann, New York (2016)
Chen, Y., et al.: The UCR time series classification archive. October 2018. https://www.cs.ucr.edu/~eamonn/time_series_data_2018
Quinlan R.: C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers, San Mateo (1993)
Breiman, L.: Mach. Learn. 45, 5–32 (2001). https://doi.org/10.1023/A:1010933404324
Adnan, M.N., Islam, M.Z.: Forest PA: constructing a decision forest by penalizing attributes used in previous trees. Expert Syst. Appl. 89, 389–403 (2017)
Islam, Md. Z., Giggins, H.: Knowledge discovery through SysFor: a systematically developed forest of multiple decision trees, In: Proceedings of the Ninth Australasian Data Mining Conference (AusDM 2011)
Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J.: Classification and regression trees. Cytometry 8, 534–535 (1987)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Grant, P., Islam, M.Z. (2022). Signal Classification Using Smooth Coefficients of Multiple Wavelets to Achieve High Accuracy from Compressed Representation of Signal. In: Chen, W., Yao, L., Cai, T., Pan, S., Shen, T., Li, X. (eds) Advanced Data Mining and Applications. ADMA 2022. Lecture Notes in Computer Science(), vol 13726. Springer, Cham. https://doi.org/10.1007/978-3-031-22137-8_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-22137-8_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22136-1
Online ISBN: 978-3-031-22137-8
eBook Packages: Computer ScienceComputer Science (R0)