Polarization in a GeV RLA

Abstract

Polarized beam dynamics in a Recirculated Linear Accelerator (RLA) differ markedly from their behavior in circular machines. After giving a brief overview of the topology of a RLA we discuss the unique requirements for polarized beam physics experiments carried at these types of machines and their implications on the spin transport. The Thomas BMT equation will be rewritten to emphasize the relevant features and the relationship between spin transport and global accelerator parameters such as the accelerating profiles. We will consider scenarios for which one or more experimental hall has to be provided with longitudinal polarization and discuss how this is achieved. Finally, a review of possible depolarization and spin precession effects occurring in these machines will be presented. In order to illustrate this, we will examine the case of the Stanford Linear Collider (SLC) where such effects were first observed.

This manuscript has been authored in part by Jefferson Science Associates, LLC under Contract No. DE-AC0506OR23177 with the U.S. Department of Energy. The United States Government and the publisher, by accepting the work for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this work, or allow others to do so, for United States Government purposes.

8.1 Topology of a Recirculated Linear Accelerator

Recirculated super conducting linear accelerators are used when high duty factor continuous beams for nuclear physics experiments are desired. Many such experiments require polarized electron sources yielding up to 90% of longitudinally or transversally polarized beams.

The beam is generated in the injector, usually with a low emittance, and accelerated in the first linac. It is then transported to the front of the next linac arranged in a 180^∘ configuration from the first one. Appropriate transport ensures that it is on crest for acceleration in the next linac. Each linac has independent cavity phasing controls and accelerating gains. The beam transport system is comprised of multi-pass spreaders and recombiners combined with standard transport arcs optimized for low emittance growth.

CEBAF [1] is one such machine where experiments demanding a high degree of polarization are carried out. Figure 8.1 shows the general layout. The beam can be accelerated through the linacs and recirculated up to five times. It can be extracted and sent to experimental halls at any given pass. Recent upgrades to CEBAF added another half pass and Hall D. We will not discuss this in the remainder of this document as this hall does not necessitate the use of polarized beams.

Fig. 8.1

CEBAF recirculator. The beam is generated in the injector where spin manipulations are performed. It is accelerated through two linacs connected by return arcs. By convention we call the return arcs near the extraction region (left of the figure) the west arcs, whereas the arcs on the opposite side are called east arcs

8.2 Helicity, Spin and Polarization

Experiments making use of polarized electron beams are studying physics processes for which the cross-section depends on the helicity of the incoming electron beam. As a reminder, helicity is defined as the projection of the spin component along the momentum. The spin of a particle is a quantum degree of freedom. For a massless photon, it can take two different values which corresponds to +1 and −1 helicities, electrons carry 1/2 and −1/2 helicities. Polarization is the weighted average of the spin states over the particle distribution. This is the quantity that is accessible via polarimetry measurements and is what we will be referring to in the rest of this document.

Polarized electrons are produced by exploiting the conservation of helicity during photo emission. A laser is passed through a linear polarizer to yield linearly polarized photons which are an equal superposition of −1 and +1 helicities. This light is then polarized circularly via a birefringent electro-optic crystal (called Pockels cells) allowing for one helicity state or the other to be dominant (typically >99.9% of circular polarization).

This light when illuminating a strained GaAs cathode will predominantly excite electrons from specific conduction bands with quantum numbers such that the helicity is conserved.

Progress in strained semiconductor superlattice photocathodes has allowed for producing polarized electrons of specific helicities with polarization of about 90% and quantum efficiency greater than 1% capable of readily producing currents of several hundreds of microamperes.

8.3 Typical Tolerances on Spin Transport for Parity Experiments

Experiments probing the conservation of parity are extremely demanding on the beam parameters. They rely upon measuring cross-section differences (asymmetries) for the two incoming electron helicity states. In order to resolve the very small parity-violating physics asymmetries, it is necessary to measure and/or suppress other helicity correlated systematic asymmetries. This includes any helicity correlated position and angle differences, beam intensity and beam envelope at the experimental target. Table 8.1 list typical beam tolerances that were achieved and those that will be required for new experiments.

Table 8.1 Beam tolerances for parity violation experiments performed and proposed at CEBAF

Note that the units are nanometers and part per billion (ppb). This refers to the time averaged value of the helicity correlated differences over the duration of the experiment. Even though the beam position monitors are only accurate to a few tens of μm, the helicity averaged difference over months of data taking reaches nanometers by virtue of accumulating enough statistics. All these experiments hinge on that critical factor.

They employ a number of methods to eliminate or reduce the systematic errors. Some have a direct bearing on the lattice design of the accelerator, others are implemented via optical manipulations on the laser table. One of the essential method is to regularly reverse the helicity of the electron beam at the experimental target in order to measure both helicity correlated beam asymmetries. This is typically implemented as a fast reversal (of the order of a few tens of Hz to kHz) and a slow reversal (once a day). The Pockels cells provide fast reversal whereas a remotely insertable optical half-wave plate (on the laser table) or a Wien filter and/or solenoidal lenses on the electron beam allow for the slow reversal.

Most experiments are only interested in receiving longitudinally polarized electrons. Nevertheless, the spin manipulations should also allow for out of plane polarization since it is sometimes requested to measure transverse spin physics asymmetries, which are of interest themselves, or must be quantified as a background to the longitudinal physics asymmetry.

Recalling the topology of a typical RLA machine such as the CEBAF accelerator, one sees that the majority of the lattice dipoles are bending in the horizontal direction.

If one neglects the synchrotron radiation effects, the spreader and recombiner sections both account for zero net vertical bending and hence do not induce any precession of the vertical spin component. Orienting the spin vertically at the start of the machine would render the transport transparent to the spin. However it is challenging to then rotate it into a longitudinal orientation at the physics target in the experimental halls at high energy. For this reason, it is injected horizontally at the start of the machine accounting for the precession across the entire lattice.

8.4 Spin Propagation in an Ideal RLA with No Synchrotron Radiation

The spin precession along an accelerator lattice is described by the Thomas BMT equation, which reads:

(8.1)

The angular velocity Ω at which the spin precesses is governed by the momentum of the beam and the magnetic and electric fields it encounters. Ignoring the transverse electric fields which are only present in the early injector in the Wien filters, we have:

$$\displaystyle \begin{aligned} \boldsymbol{\Omega}\;=\;(1+a\gamma){\mathbf{B}}_\perp+(1+a){\mathbf{B}}_\parallel \end{aligned} $$

(8.2)

This equation can be modified for the case of a RLA machine to emphasize the relevant features.

Firstly, since we are sending electrons for which the spin is oriented longitudinally, we only consider transverse magnetic field. We will treat the longitudinal magnetic fields as perturbations.

Longitudinal fields such as those arising in solenoids are only present in the injector and part of the Wien filter system. The rest of the injector solenoids are designed to be counter wound (two alternating reversed loops) to still provide focusing but result in a net zero spin precession.

Each recirculating arc bends for a total of 180^∘. A single arc will induce a precession of ϕ = πaγ. During each circulation, the beam will encounter arcs on the west and east side and accumulate more precession.

We thus write the angular rotation that the longitudinal spin component undergoes as it traverses the entire machine as [2]

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi_{n} & = &\displaystyle \frac{a}{m_e}[(n\theta_1+(n-1)\theta_2)E_0 \\ & + &\displaystyle \frac{n}{2}((n+1)\theta_1+(n-1)\theta_2)E_1+\frac{n(n-1)}{2}(\theta_1+\theta_2)E_2 \\ & + &\displaystyle (E_0+n(E_1+E_2)\theta_h)] {} \end{array} \end{aligned} $$

(8.3)

where n denotes the pass at which we extract the beam, θ₁, θ₂ and θ_h are the total bend angles on the west and east recirculation arcs and hall arc, E₀,E₁ and E₂ are the energy gains of the injector, north and south linacs respectively. For an ideal machine, the bending angles are exactly defined.

In the rest of this chapter, unless otherwise specified, we will use the Zgoubi [3] notation for spin components where Sx is the longitudinal, Sy is the transverse and Sz the vertical component.

Parameterization of spin rotation with pass number is the object of Exercise 8.7, Sect. 8.7.

8.4.1 Single Hall Case

With only one experimental hall requiring polarization, one would adjust the Wien filter to yield an integer number of π precession from the injector to the physics target. This is verified by measuring the longitudinal polarization in the halls with polarimeters (Compton, Møller). Corrections are made as necessary until the measured longitudinal polarization in the hall is maximized. Shown in Figs. 8.2 and 8.3 is the longitudinal spin component tracked through the CEBAF lattice (using Zgoubi) from the injector to the experimental halls at first pass prior and after Wien filter adjustments respectively. This was calculated for an injector gain of E_inj = 78.79 MeV and linac gains of E₁ = E₂ = 700 MeV.

Fig. 8.2

Prior to adjusting Wien filter, note the injected spin is longitudinal when the Wien filter is turned off

Fig. 8.3

After adjusting Wien filter for Hall A, note the final longitudinal polarization in Hall A is Sx = 1

8.4.2 Using the Wien Filter to Orient the Spin

A Wien filter is a device with static and electric magnetic fields orthogonal to each other and arranged in such a way as to provide a net spin rotation without deflecting the beam. Wien filters have astigmatism since they focus the beam in the plane of the electric field. That is usually compensated via external quadrupoles or a tilted pole design.

A span of $\pm \frac {\pi }{2}$ for the spin rotation is easily achieved for incoming electron beam kinetic energies of around 130 KeV (CEBAF).

The Wien filter condition can only be achieved for a monochromatic and point-like beam. Real beams have energy spread and transverse sizes, both of which will produce transverse focusing in the plane of the electric field and energy spread variations in the longitudinal plane. Proper re-matching of the transverse beam envelope is necessary in order to minimize emittance growth during subsequent acceleration.

8.4.3 Spin Flipping to Reduce Uncertainties

Many of the systematic errors caused by beam induced helicity asymmetries can be canceled by polarization reversal. As mentioned earlier, this can be done on the laser table during the generation of the circular light or by slow reversal on the electron beam.

This slow reversal is accomplished by means of a 4π spin rotator, namely a set of two Wien filters associated with a pair of solenoids [4]. The electron beam generated at the gun is longitudinally polarized. The first Wien filter is powered to produce an out of plane vertical polarization. A pair of solenoids provide a rotation of the spin back in the horizontal plane along the beam direction or 180^∘ from it providing a mean to produce a slow helicity flip. A second Wien filter is used to generate the horizontal rotation needed for compensating for the precession around the machine. Figure 8.4 shows a schematic of the system employed at CEBAF.

Fig. 8.4

CEBAF double Wien filter setup. The first Wien filter (vertical) downstream of the photo-guns rotates the polarization from longitudinal to vertical. The second Wien filter (horizontal) rotates the polarization in-plane to compensate precession of CEBAF transport magnets. Solenoids in-between ensure additional polarization rotation requirements

8.5 Spin Propagation to Multiple Experimental Halls

8.5.1 Concept of Magic Energies

In order to be able to maximize the longitudinal polarization in more than one hall, one has to constrain the choice of energy gains in the linacs to certain values. Writing Eq. 8.3 for two different experimental halls, we want to find the energy gains for which the difference $\Phi _n^{h1} -\Phi _m^{h2}$ between hall h1 and hall h2 extracted at passes n and m is an integer multiple of π.

This results in a set of available energies (so-called magic energies) as shown in Fig. 8.5. Note that this figure was produced by also imposing the constraints that the two halls have to be at different passes unless both are at pass 5 (because of the particular topology and design of the extraction system for CEBAF).

Fig. 8.5

Magic energies for longitudinal spin in two halls. Green lines depict the final energy in Hall D. Purple lines are the energy combinations between Hall A and Hall B yielding an integer number of π precession

The difference in spin precession between two experimental halls is the object of Exercise 8.7, Sect. 8.7.

8.5.2 Optimizing for Multiple Halls, Figure of Merit

Looking at Eq. (8.3), one can see that it is possible to use the linac gains as a spin rotation knob. If one configures the RLA with asymmetric acceleration for a given total accelerating gain E (E₁ + E₂ = E, E₁ ≠ E₂) then one can generate a differential spin precession between the east and west side of the machine. This method provides for an additional reach of possible configurations.

During the preparation of experimental schedules, a figure of merit taken as the square of the polarization in each hall is maximized to allow for the optimal running. Note that we assume that the halls are not current limited (the actual statistical figure of merit includes multiplying by the beam current). Typically, one hall is chosen to receive maximum polarization and energies are selected to maximize the polarization in other halls while fulfilling other experimental requirements. The calculations are arranged in a matrix (called the P² matrix) with the columns being the passes and the rows the experimental halls.

Under most circumstances, one cannot maximize the polarization in all three halls, so this figure of merit matrix allows for comparison between different scenarios. For example, the Wien filter angle necessary for maximizing the polarization in one hall can be selected and the effect on the other halls and passes is shown in the P² matrix. Various algorithms are employed to arrive at a configuration that is satisfactory for the multiple hall running and the programmatic choices made.

At this stage of planning, a simple analytical model making use of the formulas developed above and taking into account the synchrotron radiation loss in the arcs is utilized. The final determination is obtained by tracking through the lattice to map out the beam energy along the line and the resulting spin precession.

Shown in Tables 8.2 and 8.3 are the P² matrices for the planning that took part in 2019. This corresponded to E_inj = 121.5 MeV, E₁ = E₂ = 1031 MeV. As seen in these tables, maximizing the spin for Hall A at first pass also provided for a good figure of merit for B and C at pass 5 (close to 1).

Table 8.2 P² table with no Wien filter adjustment

Table 8.3 P² table with Wien filter set to maximize polarization in Hall A at first pass

Spin precession along CEBAF and P² matrix are the object of Exercise 8.7, Sect. 8.7.

8.6 Depolarization and Spin Precession Effects

8.6.1 Orbit Errors due to Lattice Imperfections

Lattice imperfections lead to imperfection resonances and affect the performance of a ring negatively. This is not the case for a RLA. One only goes through each arc once so there is no closed orbit to be perturbed by quadrupole kicks which would generate spin-orbit resonance coupling.

Consequently, misalignment errors will simply lead to extraneous dipole kicks which will affect the spin precession but not depolarize the beam.

What about intrinsic resonances arising from the interaction between the spin tune aγ and the vertical betatron oscillations in the periodic arc structures?

In theory this could produce a decoherence of the spin if one ends up on a resonance condition. The strength of such spin resonances is proportional to the Fourier spectrum of the perturbing field accumulated when the beam oscillates through the vertical plane of the quadrupoles times aγ.

Recalling the definition of polarization, one sees that depolarization can occur when particles in the beam see a different perturbing field at different phase advances leading to spin states no longer oriented in a prevailing direction. This would occur since a vertical betatron oscillation within the bunch will produce kicks that will add up coherently if on resonance with the spin tune gradually resulting in the spin of these particles spiraling away from the initial polarization direction.

The vertical betatron oscillation within the bunch is proportional to the conserved quantity which is the square root of the emittance. Fortunately, RLA machines such as CEBAF have exceedingly small emittances. At 12 GeV, the vertical emittance in CEBAF is about 1 nm.rad (geometric) for the last pass and considerably smaller on lower passes. Consequently, most RLA machines do not have to worry about spin resonances due to the beam envelope extent.

A related situation is when one has an orbit oscillation (instead of just the beam envelope) in a periodic structure. It turns out that in some cases, this can be a significant effect which will induce extraneous precession. There is no depolarization since it does not affect the spin distribution of individual particles in the bunch but instead alters the spin precession of the entire bunch.

It was observed first at the Stanford Linear Accelerator Center (SLAC) during the commissioning of the detectors for the Stanford Linear Collider (SLC).

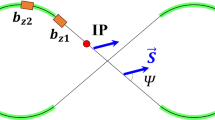
This machine was designed to collide polarized electrons and unpolarized positrons in order to produce polarized Z₀ bosons. Figure 8.6 shows its layout. After being produced, beams are stored in damping rings where their emittance is reduced. They are then accelerated in a linac to around 50 GeV and brought into collision at the interaction point (IP) by means of collider arcs.

Fig. 8.6

Stanford Linear Collider layout from [5]

The polarization needs to be longitudinal at the IP, so super-conducting solenoids located in the electron damping ring and in front of the linac allow for rotating the spin in order to accommodate the total precession. Polarimeters are located at the IP and can be used to measure the longitudinal spin component.

During commissioning, it was observed that the longitudinal polarization was very sensitive to the vertical orbit fluctuations in the arc. It had not been anticipated and prompted a number of theoretical and experimental studies which led to the realization that this was due to running near an intrinsic spin resonance resulting in extra precession.

As it turns out the collision arc is a periodic structure for which the vertical betatron tune happens to be coinciding with the spin tune when running at or near the Z₀ boson center of mass energy (about 45.6 GeV for each beam). We will explore this in an exercise dedicated to modeling the SLC arc.

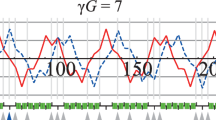
In particular, we will calculate the buildup of the vertical spin through one achromat of the north arc when near the spin resonance condition. Figures 8.7 and 8.8 show the vertical and longitudinal spin components propagating through one achromat when the vertical orbit oscillation is 0.5 mm. Figure 8.8 was obtained using Zgoubi and closely track the SLAC results in their original publications [6, 7] which was calculated at the time using spinor methods.

Fig. 8.7

Original SLAC result from [6]. In their notation, S_z is the longitudinal spin, S_y is the vertical spin

Fig. 8.8

Spin along the orbit, a calculation using Zgoubi. S_x is the longitudinal spin, S_z is the vertical spin. Also depicted is the vertical orbit deflection referenced on the right vertical axis

8.6.2 Bump Orbit Spin Rotator

In order to increase the luminosity at the IP, the SLD collaboration at SLAC decided to start using flat beams [5,6,7]. Up until then, spin precession in the collider arcs was corrected by means of the spin rotator in the damping rings and at the entrance of the linac. Optical matching of this device becomes complicated when using flat beams and would have required installing supplemental skew quadrupoles and develop a new tuning protocol. Instead, an alternative method was employed exploiting the spin orbit resonance condition.

Recall that in order to rotate the spin one needs only a combination of longitudinal and transverse fields like solenoids and dipoles. If one has a resonant condition as described above, a vertical orbit deflection will cause the spin vector to rotate in the vertical plane around an axis perpendicular to the longitudinal direction as seen in Fig. 8.8. Hence, using two orbit bumps separated by dipole magnets will act as a spin rotator. SLAC used this to very reliably adjust the spin precession for SLC even though they could not measure the orbit bumps or the orbit fluctuations with the required accuracy. Instead, they empirically mapped out the orbit bumps generated by shifting combined function dipoles from the reference orbit with the measured longitudinal polarization at the IP [6].

Figure 8.9 shows an orbit bump closed after the first seven achromats and its effect on the vertical and longitudinal spin when near resonance (45.64 GeV, left) or away from resonance, Fig. 8.10.

Fig. 8.9

42π orbit bump at 45.64 GeV

Fig. 8.10

42π orbit bump at 40 GeV

8.6.3 Effect of Energy Spread and Other Off-Momentum Errors

There are several types of energy effects to consider. The first being that particles inside the bunch will be off-momentum due to the energy spread relative to the reference momentum. For such particles, the spin is rotated by an angle δθ relative to the on-momentum particle. This results in a smearing of the longitudinal polarization but no net depolarization loss provided that the beam energy is not near a spin resonance.

Figure 8.11 shows the effect of the energy spread on the longitudinal polarization distribution at CEBAF for two values of the intrinsic energy spread.

Fig. 8.11

Effect of intrinsic energy spread on longitudinal spin

Another possibility is the beam itself being off-momentum because of synchrotron radiation and a particular choice of the magnet powering scheme.

It is effectively the case in CEBAF where the dipoles making up the arcs are powered in series by one power supply per arc which is usually set to the on-momentum value corresponding to the energy of the beam in the middle of the arc after it has been degraded by synchrotron radiation.

Hence, the first half of the dipoles is under powered while the second half is overpowered. The orbit error is compensated for by corrector magnets.

We estimate this effect by tracking through the lattice and mapping out the energy profile to use when calculating the precession. When folded in with other errors due to the calibration of the linac cavities, we typically predict the proper Wien filter setting to within a couple of degrees. The final setting is achieved by performing a polarization measurement in the halls and adjusting accordingly.

8.7 Homework

Exercise 1: Parameterization of Spin Rotation

Express the spin precession along the vertical axis in terms of the accelerating gradients in the injector, north and south linacs.

Show that it can be parameterized relative to the pass at which the beam is extracted into an experimental hall by recovering formula 8.3.

What assumptions have to be made to write the precession in this form?

Solution

Recall that the Thomas BMT equation which governs the evolution of the spin through the machine can be written as

(8.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \boldsymbol{\Omega} & = &\displaystyle (1+a\gamma){\mathbf{B}}_\perp + (1+a){\mathbf{B}}_\parallel \end{array} \end{aligned} $$

(8.5)

Starting from the expression for Ω in lab coordinates, we ignore the electric field (no source in CEBAF besides the Wien filters which we will treat separately). The other assumption we are going to make is to neglect the B_∥ component. Since we are considering transport past the injector, there is no solenoid in the rest of the machine. Other source besides solenoids would be the fringe fields at the end of the dipoles and it is a negligible effect.

Integrating Eq. 8.5 over the beam path, we end up with the spin rotation in the particle reference frame on the left side and $\int B_\perp ds$ on the right side which, when combined with the $\frac {a}{m\gamma }$ factor gives $\frac {\int B_\perp ds}{p/e} \;=\;\theta$ the rotation in the dipoles. So, θ₁,θ₂ and θ_h for the east and west recirculating arcs and the final bend into the hall.

Finally, generalizing the formula to more than one pass and parameterizing in terms of the pass n yields formula 8.3.

It can be proven by inference by realizing that for pass n, we go n times through the east side arc (θ₁), n-1 times through the west side (θ₂) and once through the bend towards the hall (θ_h).

Exercise 2: Difference in Precession Between Two Experimental Halls

Show that the difference in precession between two experimental halls can be written as $\Phi ^{h1}_{n1}-\Phi ^{h2}_{n2}\;=\;\frac {a}{m_e}f(h_1,n_1;h_2,n_2)\pi$ where h₁, h₂ are the halls A, B or C and n₁, n₂ are the passes at which the beam is extracted.

Write a program to find the combinations of energies in Hall A and Hall B for which the difference in precession between the two halls is exactly an integer number of π. This should allow to reproduce Fig. 8.5.

Solution

Starting from Eq. 8.3, we introduce the ratio $\alpha =\frac {E_0}{E_1}$ of the injector energy to the linac energy and recast it in this form:

$$\displaystyle \begin{aligned} \Phi^{h}_{n}\;=\;E_1\left(\frac{g-2}{2m_e}\right)\left[2n^2-n\left(1-2\alpha-\frac{2\theta_h}{\pi}\right)-\alpha\left(1-\frac{\theta_h}{\pi}\right)\right] \end{aligned} $$

(8.6)

We also assumed that both linacs produce the same acceleration (E₁  =  E₂) to simplify the formula.

From there, we can write the difference between halls h1 at pass n1 and h2 at pass n2 and obtain the solution.

When the quantity $E_1\left (\frac {g-2}{2m_e}\right )\left (h1,n1,h2,n2\right )$ is an integer multiple of π, both halls have the maximum polarization, this occurs for specific values of E₁, the so-called magic energies.

One can write a simple python script [8] which generates all these combinations and plot it to reproduce the figure.

Exercise 3: Spin Precession Along CEBAF; P ² Matrix

Write a program or a simple spreadsheet to calculate the spin precession along the CEBAF machine for various passes and energies.

Using Sand’s formula, the loss per arc can be approximated to

$$\displaystyle \begin{aligned} \Delta E\;=\;0.08846 E^4 \frac{\pi n_d}{2 l_d}\end{aligned}$$

with n_d the number of dipoles in an arc and l_d the length of the trajectory in a dipole. Calculate the P² matrix and Wien filter settings required for each hall. For scheduling purposes, it is acceptable if the P² in a given hall is above 0.8. Besides Hall B, which other combinations of halls and passes are acceptable when we are maximizing the polarization for Hall B at pass 5?

Solution

The spreadsheet, spinprecessionCEBAFRLA [9], implements the calculation as described above. The gains for the North and South linacs are entered in E2 and F2. The injector gain is automatically calculated in D2. Precession is calculated around the machine using the simplified expression of the Thomas BMT equation 8.3 and the resulting P² matrix available in cells C23 thru G28. The table labeled wien required give the necessary Wien angle to maximize the longitudinal polarization for a particular pass and hall. Finally, the cell C7 provides a mean to turn on (1) or off (0) the synchrotron radiation.