Abstract
We present a demonstration of Andreoli’s focusing theorem for proofs of linear logic (MALL) that avoids directly reasoning on sequent calculus proofs. Following Andreoli-Maieli’s strategy, exploited in the MLL case, we prove the focusing theorem as a particular sequentialization strategy for MALL proof nets that are in canonical form. Canonical proof nets satisfy the property that asynchronous links are always ready to sequentialization while synchronous focusing links represent clusters of links that are hereditarily ready to sequentialization.
Supported by Istituto Nazionale di Alta Matematica “Francesco Severi” (INdAM).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Compared with the syntax of [6], monomial proof structures [8] are technically simpler; they allow us to easily extend to the MALL case arguments originally used for the MLL case such as Laurent’s Splitting Lemma [7] and Andreoli-Maieli’s Focusing Theorem [2]. Monomial proof structures have a natural presentation in terms of Coherent Spaces [4] and their correctness criterion can be also formulated in terms of “graph retraction steps” à la Danos [9].
- 2.
The dependence condition corresponds to the resolution condition of [6].
- 3.
Observe that in general substitutions may not preserve the property of being a proof structure.
- 4.
The logical degree of a formula F, denoted \(\partial (F)\), is defined by induction on the height of F: if F is atomic then \(\partial (F)=0\), else F has the form \(F_1\circ F_2\), with
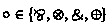 , and \(\partial (F)=\partial (F_1)+\partial (F_2)+1\).
, and \(\partial (F)=\partial (F_1)+\partial (F_2)+1\). - 5.
Note that a \(J(\pi )\) differs from a switching \(S(\pi )\) for the following facts: (i) we do not consider slices, (ii) we do not mutilate premises and (iii) there can be multiple (possibly, none) jumps exiting from a
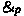 -node and going to different nodes depending on p or \(C_p\) nodes.
-node and going to different nodes depending on p or \(C_p\) nodes.
References
Andreoli, J.-M.: Logic programming with focusing proofs in linear logic. JLC 2(3), 297–347 (1992). https://doi.org/10.1093/logcom/2.3.297
Andreoli, J.-M., Maieli, R.: Focusing and proof-nets in linear and non-commutative logic. In: Ganzinger, H., McAllester, D., Voronkov, A. (eds.) LPAR 1999. LNCS (LNAI), vol. 1705, pp. 320–336. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48242-3_20
Danos, V., Regnier, L.: The structure of multiplicatives. AML 28, 181–203 (1989). https://doi.org/10.1007/BF01622878
Girard, J.-Y.: Linear logic. TCS 50, 1–102 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Girard, J.-Y.: Proof-nets: the parallel syntax for proof theory. In: Logic and Algebra (1996). https://doi.org/10.1201/9780203748671
Hughes, D., Van Glabbeek, R.: Proof nets for unit-free multiplicative-additive linear logic. In: Proceedings of IEEE Logic in Computer Science (2003). https://doi.org/10.1109/LICS.2003.1210039
Laurent, O.: Sequentialization of multiplicative proof nets. Manuscript, April 2013. https://perso.ens-lyon.fr/olivier.laurent/seqmll.pdf
Laurent, O., Maieli, R.: Cut elimination for monomial MALL proof nets. In: LICS 2008 (2008). https://doi.org/10.1109/LICS.2008.31
Maieli, R.: Retractile proof nets of the purely multiplicative and additive fragment of linear logic. In: Dershowitz, N., Voronkov, A. (eds.) LPAR 2007. LNCS (LNAI), vol. 4790, pp. 363–377. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75560-9_27
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Maieli, R. (2022). A Proof of the Focusing Theorem via MALL Proof Nets. In: Ciabattoni, A., Pimentel, E., de Queiroz, R.J.G.B. (eds) Logic, Language, Information, and Computation. WoLLIC 2022. Lecture Notes in Computer Science, vol 13468. Springer, Cham. https://doi.org/10.1007/978-3-031-15298-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-15298-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-15297-9
Online ISBN: 978-3-031-15298-6
eBook Packages: Computer ScienceComputer Science (R0)


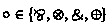 , and
, and 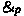 -node and going to different nodes depending on p or
-node and going to different nodes depending on p or 