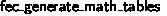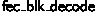Abstract
Most methods of data transmission and storage are prone to errors, leading to data loss. Forward erasure correction (FEC) is a method to allow data to be recovered in the presence of errors by encoding the data with redundant parity information determined by an error-correcting code. There are dozens of classes of such codes, many based on sophisticated mathematics, making them difficult to verify using automated tools. In this paper, we present a formal, machine-checked proof of a C implementation of FEC based on Reed-Solomon coding. The C code has been actively used in network defenses for over 25 years, but the algorithm it implements was partially unpublished, and it uses certain optimizations whose correctness was unknown even to the code’s authors. We use Coq’s Mathematical Components library to prove the algorithm’s correctness and the Verified Software Toolchain to prove that the C program correctly implements this algorithm, connecting both using a modular, well-encapsulated structure that could easily be used to verify a high-speed, hardware version of this FEC. This is the first end-to-end, formal proof of a real-world FEC implementation; we verified all previously unknown optimizations and found a latent bug in the code.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords


1 Introduction
As part of a larger project of ensuring reliable networks, we are applying formal functional-correctness verification to network components: machine-checked proofs that C programs (and, eventually, P4 programs and FPGAs) satisfy their high-level functional specs. When attackers may gain access to the source code and analyze it for bugs and vulnerabilities, we want something stronger than software testing or conventional static analysis: we want a proof that the software works no matter what input is provided, no matter how dastardly. And we want a proof that the program works correctly, not merely that it does not crash.
One key to reliable networking is forward erasure correction (FEC): in a portion of the network in which packets are being lost, add extra parity packets that allow reconstruction of lost packets without retransmission. We use an FEC algorithm and C program that have been in active use for over 25 years. The program does many clever and not-so-clever things, and comments indicate that some parts are not fully trusted even by its original authors.
This FEC is a particularly intriguing target for verification because its high-level correctness depends on fairly intricate mathematics—we must reason about polynomials, matrices, and finite fields. Meanwhile, the C implementation’s correctness relies on C programming features and careful manipulation of pointers in memory. Thus, we need a tool that can reason at both of these levels. We use the Coq proof assistant, utilizing the Mathematical Components [10] (MathComp) library for the high-level reasoning and the Verified Software Toolchain [6] (VST) for the C program verification.Footnote 1 Our VST specs are written using separation logic, in which we specify precisely what memory is read from and written to as well as all external effects (I/O, system calls, etc.). This gives us a blanket containment property: the C function is guaranteed to only interact with the outside world (memory, OS, etc.) in ways stated in the spec.
Contributions
-
1.
We show that formal verification can prove functional correctness for a C program that uses both intricate mathematics and clever C programming tricks. This is the first formally verified FEC instance that connects a high-level mathematical specification with an efficient, optimized implementation.
-
2.
We formally prove the correctness of a particular version of Reed-Solomon erasure coding, parts of which were unpublished. Further, we prove that an optimization in the C code, a heavily restricted form of Gaussian elimination, is sufficient for this application; this was unknown to the code’s authors.
-
3.
For the first time, we utilize both MathComp and VST in the same project. The two libraries differ greatly in types, tactics, and styles of proof; we use both by separating our functional specification into two layers in a process that we expect can be automated.
-
4.
We demonstrate our methods on a real-world C program, verified as is, except for two tiny changes, one of which is to fix a latent bug that we discovered.
1.1 Forward Erasure Correction
When transmitting data over a noisy channel, one can use an error-correcting code—adding generalized “parity” bits, sending the data across the channel, and then decoding to recover the data if any errors occurred; this technique is known as forward error correction. In an erasure code, the locations of the missing data are known to the decoder; this allows correction of more errors.
FEC is useful in any network where non-congestion-related packet loss is frequent and retransmission is infeasible or expensive. For instance, wireless networks are especially prone to packet loss due to interference or jamming. More generally, errors in network devices due to firmware bugs, misconfiguration, or malware can lead to dropped packets. In these cases, retransmission with TCP is not desirable, because TCP will incorrectly interpret these losses as congestion, grinding the network to a halt. Similarly, applications such as video or audio streaming, often run over UDP, cannot handle retransmission without additional work; moreover, the latency of retransmitting is often too high. Thus, FEC continues to be important in ensuring network reliability.
The algorithm we consider is based on Reed-Solomon [24] coding; it groups the input bits into symbols representing elements of a finite field and interprets the data as a polynomial over this field. Reed-Solomon codes are particularly useful for correcting burst errors—errors that occur sequentially—since \(n+1\) consecutive bit errors can only affect at most 2 symbols of length n. Reed-Solomon decoders can be quite complex, both in theory and implementation; many mechanisms have been developed for this purpose. Nevertheless, these codes have been heavily used in applications such as CDs, DVDs, Blu-Ray disks, hard drives, and satellite communications [27].
In the early 1990’s, there was a flurry of activity in Reed-Solomon erasure coding. McAuley described [18] and patented [19] a method for FEC based on Reed-Solomon coding for use in network transmission. Rabin [23] described an alternate technique for information dispersal, which was further developed by Preparata [22], Schwarz [25], and others, mainly for use in RAID storage systems; Plank [21] provides a tutorial and explanation. McAuley later wrote a C implementation of FEC for network packets based on this second technique with several further modifications. We will refer to the algorithm implemented by McAuley’s C code as the Reed-Solomon Erasure (RSE) code.
Bellcore (now Peraton Labs) has employed this FEC algorithm (and implementation) successfully in numerous networking projects to support resilient communication, most recently in the DARPA EdgeCT program. McAuley’s implementation includes many optimizations and modifications to the core algorithm, including some whose correctness was unknown to the code’s authors (Sect. 5.2). It had one bug that we corrected (Sect. 6.6). We have produced a formal, machine-checked proof that this FEC implementation correctly recovers data in the presence of erasures—we proved the algorithm correct and proved that the program correctly implements it.
1.2 Coq and VST
We use the Coq interactive theorem prover, in which the user states and proves theorems in a higher-order dependently typed logic. These theorems are mechanically checked by the Coq kernel. Proofs can be (semi)automated by Coq’s built-in tactics and by user-defined tactic programming.
Coq has been widely used in program verification and formalized mathematics. One particularly important verification effort is CompCert [15], an optimizing C compiler written and proved correct in Coq. That is, CompCert comes with a formal proof that the assembly code generated by the compiler preserves the semantics of the input C program.
VST is a program logic and set of proof automation tools that enables the verification of C programs in Coq. Using VST, one can write a specification for each C function, stating its preconditions (properties that must hold before the function is run) and postconditions (properties that must hold when the function finishes). These properties can involve both C-specific assertions (e.g., about the contents of memory) and arbitrary statements in Coq’s logic. Then, using custom tactics and proof automation included with VST, the user can prove in Coq that the C function satisfies its specification.
VST’s program logic is proved sound, with a machine-checked proof in Coq. When we prove that McAuley’s RSE correctly reconstructs missing packets, the soundness proof guarantees that the assembly-language program generated by the CompCert C compiler really has that behavior. VST is formally proved sound for CompCert, but not for gcc or clang. VST is intended (and believed) to be sound for gcc/clang; its program logic has stricter rules than would be necessary only for soundness w.r.t. CompCert. For example, for signed integer arithmetic, where CompCert is (unfortunately) a refinement of C11 (CompCert wraps while C11 is u.b.), VST imposes the (more abstract) C11 spec. Thus, VST proofs about C programs also provide useful (though less foundational) assurance about programs compiled with other compilers.
While conventional separation logics have spatial conjuncts that are predicates just on memory resources, VST’s separation logic has spatial conjunct predicates on both memory locations and the outside world, which one might affect by performing IO or making a system call [17, Section 3]. In our project, none of the VST funspecs mention the outside world in the precondition or postcondition; this means, like any Hoare triple in separation logic, that those functions can neither access nor modify that resource.
Proving that a C program satisfies a specification is quite challenging. We must prove low-level correctness properties (the program does not crash, all memory accesses are valid, etc.) and provide loop invariants and intermediate proofs to prove high-level properties (that the function satisfies its spec). Though VST’s proof automation is able to hide some of this complexity, many parts must still be done manually. Dealing with heavily optimized C code that was never intended to be verified makes these tasks substantially more complicated.
Section 2 describes the RSE algorithm, which differs in several ways from the technique described by Rabin, Preparata, and Schwarz. Section 3 explains the different verification tasks, including defining a functional model of the algorithm and showing with VST that the C code implements this model. Section 4 describes the functional model, Sect. 5 discusses the verification of this functional model, including the proof that the algorithm correctly reconstructs missing packets, and Sect. 6 discusses the proofs about the C code. Section 7 and Sect. 8 give related and future work.
2 The RSE Algorithm
Like all Reed-Solomon codes, the algorithm treats input symbols as elements of a finite field and interprets the input sequence of words as the coefficients of a polynomial over this field. However, both the C implementation and the RSE algorithm are more naturally described using linear algebra and matrix operations.
Let D be the input data, which consists of k packets, each of length at most c bytes. If any packets are smaller, fill in the missing entries with zeroes so that D is a \(k \times c\) matrix. Let h be the number of parity packets we wish to append. We will be able to reconstruct up to h total packet-drops.
Let \(k_{max}\) and \(h_{max}\) be (fixed) parameters such that \(k \le k_{max}\) and \(h \le h_{max}\). Let \(n_{max}= h_{max}+ k_{max}\) (maximum number of packets per batch) and let F be a field such that \(|F| > n_{max}\).
2.1 Initialization
First, we generate a Vandermonde matrix of size \(h_{max}\times n_{max}\); that is, take \(n_{max}\) distinct nonzero elements of F, denoted as \(\alpha _1, \alpha _2, ..., \alpha _{n_{max}}\), and generate the following matrix:
Then, we run Gaussian elimination (see Sect. 4.2) on this matrix to get the row-reduced form, which consists of the identity matrix followed by W, the \(h_{max}\times k_{max}\) weight matrix:
2.2 Encoding
The encoder receives as input the data D, a \(k \times c\) matrix. Let \(W'\) be the submatrix of W consisting of the first h rows and the first k columns. The encoder computes \(P = W'D\), an \(h\times c\) matrix. These are the parity packets that are sent (along with the original data) to the receiver.

2.3 Decoding
The decoder is significantly more complicated. However, if no packets are lost, the decoder simply returns the first k packets; only if packets are dropped does the following algorithm need to be invoked. To give some intuition, we will first present the decoder for a special case before giving the full algorithm.
Since this is an erasure code, we know the locations of the missing packets; we also require that the total number of missing packets is at most h.
For a special case, suppose that the last h data packets were lost and all parity packets were received. We can think of the original data D as a block matrix consisting of \(D_1\), the \((k - h) \times c\) matrix of the received data, and \(D_2\), the \(h \times c\) matrix of the lost data. Similarly, we can split the \(h \times k\) matrix \(W'\) (from the encoder) into \(W'_1\), consisting of the first \(k - h\) columns of \(W'\), and \(W'_2\), consisting of the rest.

From this, the missing data \(D_2\) can be computed using P, \(D_1\), and the parts of \(W'\), all of which are known:
The general case is similar, but we need to define the relevant submatrices more carefully. Let \( xh \) be the number of missing data packets. We must have received at least \( xh \) parity packets (or else the total number of missing packets is more than h). Let \(P'\) be the submatrix of P consisting of the first \( xh \) received parity packets. This time, we let \(W'_1\) be the \( xh \times (k - xh )\) submatrix of \(W'\) whose rows consist of the locations of the \( xh \) found parity packets and whose columns consist of the \(k - xh \) locations of the received data. Let \(W'_2\) be the \( xh \times xh \) submatrix of \(W'\) whose rows consist of the locations of the \( xh \) found parities and whose columns consist of the locations of the missing data. Finally, \(D_1\) and \(D_2\) are still defined such that \(D_1\) contains the received rows and \(D_2\) contains the missing rows. This time, these rows need not be contiguous. These definitions reduce to the previous ones in the special case considered above.
By the definitions of the above submatrices, Eq. 2 still holds (except that we replace P with \(P'\)), so we can find the missing data \(D_2\) by computing \((W'_2)^{-1}(P' - W_1'D_1)\).
This decoder is only well defined if \(W_2'\) is invertible. \(W_2'\) is dynamically chosen based on the found parities and missing data, so we must show a stronger claim that any square submatrix up to size \(h \times h\) of W is invertible. Proving this was the crucial step in the functional model verification, described in Sect. 5.1.
As noted in Sect. 1.1, this algorithm is a modified version of the technique described by Rabin, Preparata, Schwarz, and others. The main difference is the use of the static weight matrix in RSE; all the others assume that the Vandermonde matrix has dimensions \(h \times (k+h)\) and exactly h packets are lost. Thus, their needed correctness property is weaker; it requires only that any \(h \times h\) submatrix of W is invertible.
3 Verification Structure
The verification consists of two distinct tasks: we prove that the RSE algorithm is correct (i.e., the decoder recovers the original data in the presence of errors) and that the C program truly implements this algorithm. These two tasks are quite different; the first is purely mathematical and involves proofs about linear algebra, while the second involves implementation details and C-language verification conditions. To separate these tasks and make the proofs more modular, we define a functional model, a purely functional program written in Coq that implements the RSE algorithm. This functional model is inefficient but easy to reason about in Coq. Then we use VST to prove that the C program refines this functional model. Finally, we compose these two parts to produce a formal proof that the C implementation of this erasure code is correct.
Separating the functional specification and the VST proofs is a common paradigm; it has been used to verify SHA-256 hashing [4], HMAC-DRBG cryptographic random number generation [28], and floating-point numerical programming [5]. This approach provides a clear formal specification independent of any implementation; we can reuse the same functional model and its correctness proofs to verify another implementation of this algorithm (for instance, an FPGA version). It makes verification more flexible; we can prove further properties later simply by adding additional lemmas about the functional model. It makes the proofs shorter and clearer; we can tell which parts are needed for the core correctness proofs and which are implementation-specific. Finally, it permits a separation of expertise: the person who proves mathematical theorems about the functional model need not know anything about C programming or VST verification, and the person who proves C refinement in VST need not know why the functional model accomplishes the high-level goals.
Our functional model was written in Gallina, the functional programming language embedded in Coq, using the Mathematical Components (MathComp) library for formalized mathematics. MathComp contains definitions and theorems about groups, rings, fields, vector spaces, matrices, polynomials, graphs, and other mathematical objects.
In fact, we define two functional models—a high-level version uses MathComp’s abstract and dependent types of matrices, polynomials, and the like, while a low-level version uses concrete types such as  , which VST can use to represent memory contents. Translating between these types is nontrivial (because of all the dependent types in MathComp), so we separate the type conversion proofs from both the high-level mathematical reasoning and the low-level VST refinement proof. This makes the proofs more modular and helps to improve the readability of the resulting formalization. The translation is largely mechanical and we expect that it could be automated; we focus on the high-level functional model and the VST refinement proofs.
, which VST can use to represent memory contents. Translating between these types is nontrivial (because of all the dependent types in MathComp), so we separate the type conversion proofs from both the high-level mathematical reasoning and the low-level VST refinement proof. This makes the proofs more modular and helps to improve the readability of the resulting formalization. The translation is largely mechanical and we expect that it could be automated; we focus on the high-level functional model and the VST refinement proofs.
4 Functional Model
4.1 The Encoder and Decoder
We translate Eq. 1 into the language of Coq/MathComp:

 denotes a matrix of size \(x \times y\) over field F and
denotes a matrix of size \(x \times y\) over field F and  denotes matrix multiplication. The type
denotes matrix multiplication. The type  represents an ordinal, a natural number in the range \([0, n - 1]\). The encoder takes in the parameters h, k, c, \(h_{max}\), and \(n_{max}\) (all defined as in §2), the \(h_{max}\times n_{max}\) weight matrix, the \(k \times c\) data matrix, and proofs that h and k are bounded appropriately.
represents an ordinal, a natural number in the range \([0, n - 1]\). The encoder takes in the parameters h, k, c, \(h_{max}\), and \(n_{max}\) (all defined as in §2), the \(h_{max}\times n_{max}\) weight matrix, the \(k \times c\) data matrix, and proofs that h and k are bounded appropriately.  creates a submatrix from an input matrix by selecting rows and columns via user-specified functions.
creates a submatrix from an input matrix by selecting rows and columns via user-specified functions.  is needed to handle some dependent type casting; it has no computational content and can be ignored. Finally,
is needed to handle some dependent type casting; it has no computational content and can be ignored. Finally,  selects the “opposite” ordinal; for
selects the “opposite” ordinal; for  ,
,  . Therefore, this function selects the first h rows and the last k columns (in reverse order) of the weight matrix and multiplies this by the input. This differs from the algorithm in Sect. 2.2, which selects the first k columns. The overall algorithm’s correctness is not affected as long as we choose the matrices \(W_1'\) and \(W_2'\) in the decoder to be consistent, but this change makes the model consistent with the C implementation (see Sect. 6.2).
. Therefore, this function selects the first h rows and the last k columns (in reverse order) of the weight matrix and multiplies this by the input. This differs from the algorithm in Sect. 2.2, which selects the first k columns. The overall algorithm’s correctness is not affected as long as we choose the matrices \(W_1'\) and \(W_2'\) in the decoder to be consistent, but this change makes the model consistent with the C implementation (see Sect. 6.2).
The decoder (Eq. 2) can be similarly translated into MathComp; we omit the full definition, but note that we defined the decoder more generally than needed: it is defined over any field and over any Vandermonde matrix on distinct elements of that field.

4.2 Gaussian Elimination
Gaussian elimination, or row reduction, is a well known algorithm in linear algebra for solving systems of linear equations, finding matrix inverses, and calculating determinants. The C code includes an implementation of Gaussian elimination, used to row-reduce the Vandermonde matrix to produce the weight matrix and to invert \(W_2'\) in the decoder. Thus, we need to define a corresponding functional model.
Gaussian elimination proceeds by applying a sequence of elementary row operations—swapping two rows, multiplying a row by a scalar, and adding a scalar multiple of one row to another row—to a matrix until it is in row-echelon form, which for full-rank matrices (including all relevant matrices in this application) means that the left hand side becomes the identity matrix. Crucially, these row operations preserve invertibility because each corresponds to left multiplication by an (invertible) elementary matrix.
The order of the row operations may vary; Algorithm 1 describes one concrete implementation of Gaussian elimination (we use 0-indexing to be consistent with MathComp). While translating this into MathComp is largely straightforward, it turns out that the C program does not actually implement Algorithm 1. Rather, rows are never swapped and at each iteration, all entries in column c must be nonzero.
The following excerpt from the C code, with the original comments, shows the error checks to ensure this condition. The code is mainly interesting for the error checks and comments, but we briefly detail how it works: the  guard value never changes; instead for current column
guard value never changes; instead for current column  , the code iterates through rows
, the code iterates through rows  . The second conditional checks if matrix element
. The second conditional checks if matrix element  is nonzero for swapping (but returns an error because swapping is not implemented), while the first conditional breaks out of the loop with an error when
is nonzero for swapping (but returns an error because swapping is not implemented), while the first conditional breaks out of the loop with an error when  has reached the last row.
has reached the last row.

The “swap rows” and “Not done yet!” messages suggest that the authors intended to (eventually) implement the full algorithm. The error checks indicate that the authors were not sure if these errors could be triggered.
We will call this algorithm “Restricted” Gaussian elimination (Algorithm 2). Once again, defining this function in MathComp is not difficult, but proving that this limited form of Gaussian elimination suffices was a major part of the functional model verification (Sect. 5.2).

4.3 Field Operations
The encoder, decoder, and Gaussian elimination work over any field, but the C implementation uses the field \(GF(2^8)\), which we must define. Mathematically, this field is isomorphic to \(\mathbb {F}_2[x]/(1 + x^2 + x^3 + x^4 + x^8)\). That is, the elements of this field are polynomials of degree at most 7 with coefficients in \(\mathbb {F}_2\) (the field of two elements), and all operations are performed modulo \(1 + x^2 + x^3 + x^4 + x^8\). The choice of \(\mathbb {F}_2\) is important; it allows us to represent polynomials as sequences of bits. Since the polynomials are of degree at most 7, all field elements can be represented as bytes.
This field and its construction are well understood; while MathComp did not include the construction of finite fields via quotients, we were able to define and prove general results about primitive polynomials and the finite field’s construction without much issue. Then, we can prove correct the method the C code uses to populate the lookup tables used to compute in this field (Sect. 6.4).
One difficulty in using this field is the difference between the polynomials we used to define the field and the bytes that we would like to represent as field elements. To avoid manually converting everywhere, we defined another field structure directly on the  type and used Coq’s Canonical Structures.
type and used Coq’s Canonical Structures.
5 Verifying the Functional Model
5.1 Decoder Correctness
To prove the RSE algorithm correct, we need to prove that the decoder actually reconstructs the original packets. That is, if the data and parity packets that were marked as “received” are correct and there are at most h missing packets, then running the decoder on the received packets should recover the original data. We state this in Coq below:

This theorem is expressed entirely in terms of MathComp matrices and operations; it does not rely on the C implementation at all. Its proof requires two main tasks: showing that \(W'_2\) is invertible and proving that the sequence of operations in the decoder is sufficient to recover the original data. The second task is fairly straightforward; we compare the matrices elementwise. Thus, the main challenge comes from proving the invertibility of the submatrix \(W'_2\).
Proving the Invertibility of \(\boldsymbol{W'_2}\). Recall that \(W_2'\) is a dynamically chosen submatrix of W, the right submatrix of the row-reduced Vandermonde matrix V. Therefore, we want to prove the following theorem ( ):
):
Theorem 1
Let V be an \(m \times n\) row-reduced Vandermonde matrix on distinct elements. Let \(m \le n\) and \(z \le \min (m, n-m)\). Let Y be the submatrix of V formed by taking z rows of V and z of the last \((n - m)\) columns of V. Then Y is invertible.
Formally proving this theorem in Coq is quite complicated, partly because MathComp does not include many of the definitions and results that we need. Namely, we need to define and prove properties about row operations and Vandermonde matrices, including the following well-known property ( ):
):
Theorem 2
Let V be an \(n \times n\) Vandermonde matrix on distinct nonzero elements. Then V is invertible.
The proof relies on the fact that a degree n polynomial with \(n+1\) zeroes is identically zero, a fact already included in MathComp. This marks the only direct use of polynomial properties (other than in the finite field construction); the rest of the results are purely based on linear algebra.
Note that the only property we required of the weight matrix W was that every \(z \times z\) submatrix is invertible. Row-reduced Vandermonde matrices satisfy this property, but any other matrix that satisfies this property could be used, and the encoding-decoding scheme would still be correct.
5.2 Gaussian Elimination
Proving full Gaussian elimination (Algorithm 1) correct is fairly standard (though nontrivial to formalize completely in Coq), since the algorithm is very well-understood.
The real challenge is to determine the conditions under which RGE (Algorithm 2) will return the same result as Algorithm 1. It is easy to see that if the error case is never reached, then the two algorithms are equivalent. But it is not at all obvious how to avoid triggering the error. Invertibility is a necessary but quite insufficient condition; for instance, the restricted algorithm fails on diagonal and triangular matrices. Therefore, we had two tasks: determine the class of matrices for which RGE works correctly and prove that the matrices used in the RSE algorithm are in this class.
For the first task, we needed to determine when certain elements will be zero or nonzero at a given step in Gaussian elimination. This is difficult, since the elements are constantly changing; instead, we transformed the condition into a statement about the invertibility of certain submatrices, since Gaussian elimination preserves invertibility.
During the rth step of Gaussian elimination (assuming no error was reached), the \(r \times r\) upper-left submatrix is a diagonal matrix with nonzero elements along the diagonal; all other elements in the first r columns are zero. With this, we defined the submatrix \(C_k^r\) (for \(k < r\)) as the submatrix of A consisting of the first r rows and the first \(r+1\) columns except column k. Then, for \(k < r\), \(A_{k, r} \ne 0\) exactly when \(C_k^r\) is invertible (we prove this by showing that the rows of \(C_k^r\) are linearly independent). We can do something similar for \(k \ge r\); this time we consider \(R_k^r\), defined to be the submatrix of A consisting of the first \(r+1\) columns and rows \(\lbrace 0, 1, \ldots r-1, k\rbrace \). Similarly, \(R_k^r\) is invertible iff \(A_{k, r} \ne 0\). We will say that A is strongly invertible if, for all \(0 \le r < m\), \(C_k^r\) is invertible for all \(k < r\) and \(R_k^r\) is invertible for all \(k \ge r\). Finally, we prove that RGE is equivalent to full Gaussian elimination iff input A is strongly invertible.
Note that this condition requires a particular set of \(m^2\) submatrices of the input \(m \times n\) matrix to be invertible, quite a difficult condition to satisfy. However, in this application, Gaussian elimination is applied to only two kinds of matrices: the matrices \(W_2'\) in the decoder and a Vandermonde matrix on \(x^{n_{max}- 2}, \ldots , x^2, x, 1\) (where x is the primitive element of the field). The strong invertibility of each ultimately follows from properties of Vandermonde matrices: the result for the first matrix follows from Theorem 1, while the result for the second is harder to show, but ultimately follows from repeated applications of Theorem 2 and use of the fact that the field elements are consecutive powers of the primitive element. With this, we proved the previously unknown result that RGE suffices for this application and that the errors shown in Sect. 4.2 are never reached.
6 Verifying the Implementation
The C code consists of five primary functions with the following signatures:

Each of these functions has a corresponding VST specification. We first describe key implementation differences and verification challenges, then discuss the specs for selected functions in Sect. 6.4 and Sect. 6.5.
6.1 Implementation Differences from Algorithm
Broadly, the C code implements the RSE algorithm from Sect. 2 with the parameters \(k_{max}= 127\) and \(h_{max}= 128\) (as well as a bound of 16000 on c, but this does not affect the correctness). However, neither this algorithm nor the functional model precisely align with the C implementation. Instead, the implementation makes a few changes, and we must prove that these changes do not modify the algorithm’s behavior:
-
The code uses Restricted Gaussian Elimination rather than Gaussian elimination; see Sect. 5.2.
-
The encoder described in Sect. 2.2 takes \(W'\) to be the submatrix consisting of the first h rows and the first k columns. But the implementation takes the last k columns in reverse order (and likewise for the decoder) because of how the weight matrix is arranged in memory.
-
In the decoder, rather than computing \(P - W_1'D_1\) with a multiplication followed by a subtraction, the implementation does this via a single larger multiplication, taking advantage of the fact that the left hand side of the weight matrix is the identity. The result of the computation is equivalent (though this is not completely trivial), but it is unclear why the authors chose this.
-
Due to the representation of matrices in memory, the decoder computes the last matrix multiplication by implicitly reversing the rows of the first matrix and the columns of the second one. Equivalence with standard matrix multiplication is not too hard to prove thanks to MathComp’s utilities for iterated summations.
-
The code takes as input a sequence of variable-length packets, and we want to recover the original data once the decoder has finished. The RSE algorithm only describes how to generate the recovered packets, but the implementation has to put each packet pointer in its correct position in the packet array and ensure that the length for each packet is correct. The functional model includes filling in missing packets, but it uses matrices of uniform length.
6.2 Implementation-Specific Verification Challenges
Aside from differences between the algorithm and implementation, the C code, first written 25 years ago and last modified over 15 years ago, does several things that make it poorly suited to verification:
-
Matrices are represented in memory very inconsistently: as pointers, global 2D arrays, local 2D arrays treated as though they were 1D arrays, and arrays of pointers to each row. The C code freely converts between these types; therefore, we had to prove several general results in VST to improve support for 2D arrays and pointer arithmetic. For example, to convert between 1D and 2D arrays, we prove that a 2D array in memory containing Coq list-of-lists
 is equal to storing a 1D array containing
is equal to storing a 1D array containing 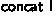 , all of the inner lists of
, all of the inner lists of  concatenated together. This lemma is generic and will be added to VST for future use. For dealing with arrays of pointers, we used VST’s
concatenated together. This lemma is generic and will be added to VST for future use. For dealing with arrays of pointers, we used VST’s 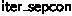 , which represents iterated separating conjunction over a collection of predicates, and we proved lemmas allowing us to extract and modify a single element of the collection. Additionally, we needed several smaller lemmas and tactics for handling the resulting pointer-equality proof obligations arising from these type conversions and for simplifying the pointer comparisons in loop guards, which we plan to contribute to VST in order to improve the handling of pointer arithmetic.
, which represents iterated separating conjunction over a collection of predicates, and we proved lemmas allowing us to extract and modify a single element of the collection. Additionally, we needed several smaller lemmas and tactics for handling the resulting pointer-equality proof obligations arising from these type conversions and for simplifying the pointer comparisons in loop guards, which we plan to contribute to VST in order to improve the handling of pointer arithmetic. -
Field multiplication is frequently called in a loop, so it was written as a macro rather than a function. VST’s front end expands macros, so we would have to prove the correctness of multiplication every time it is used. To avoid this, we changed the macro to a function. This did not have any effect on performance; at gcc optimization level O2 and O3, the performance was the same, and at level O3, the function was inlined.
-
The C function for the decoder includes about 30 local variables (including stack-allocated arrays with tens of thousands of elements) and several layers of nested loops; VST became quite slow due to the extremely large context. This required significant proof engineering to make verification feasible, including the use of opaque constants to stop giant arrays from being unfolded and heavy use of the frame rule, which allows one to “frame out” parts of the context which are not needed and recover them later, to verify each loop independently.
-
The code accesses memory using an inconsistent mix of pointer arithmetic, array indexing, and combinations of both. The VST proof obligations are different in these cases, and we need some auxiliary assertions about equality of memory locations and pointer arithmetic to reason about these dereferences.
6.3 VST Specifications
A C specification in VST looks like:

where f is the function name, \( param\_typs \) are the C function parameter types, \( ret\_ty \) is the C return type, \( params \) are the (symbolic) values of the function parameters, \( globs \) are the global variables, and \( ret \) is the (symbolic) return value. The entire PRE block represents the precondition, which must hold before the function is run. The POST block is the postcondition, which is true after the function finishes. \( p1 \) and \( p2 \) are propositions in Coq’s logic, while \( s1 \) and \( s2 \) are propositions in separation logic—they describe the contents of memory. Finally, the variables \(\vec {v}\) in the WITH clause are logical variables, abstract mathematical values to which the precondition and postcondition can refer.
6.4 Verifying 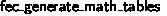
The first C function is  , the function that generates the power, logarithm, and inverse tables for the field elements. This function, like the others, is interesting because of how it modifies memory, not because of what it returns; thus the interesting part of the VST spec is the SEP clause. The precondition’s SEP clause says that the global array
, the function that generates the power, logarithm, and inverse tables for the field elements. This function, like the others, is interesting because of how it modifies memory, not because of what it returns; thus the interesting part of the VST spec is the SEP clause. The precondition’s SEP clause says that the global array  (the power table) initially stores
(the power table) initially stores  zeroes. In the postcondition, this global array now stores the Coq list
zeroes. In the postcondition, this global array now stores the Coq list  , which we define as the powers of field element x (the ith entry contains \(x^i\)). We have similar Coq lists and pre- and post-conditions for the log table and inverse table.
, which we define as the powers of field element x (the ith entry contains \(x^i\)). We have similar Coq lists and pre- and post-conditions for the log table and inverse table.
Proving that the field table generation is correct is largely straightforward, given the field definitions described in Sect. 4.3. However, there were two main complications. The first comes from the method of populating the tables: compute \(x^i\) for all \(0 \le i < 256\) by repeatedly multiplying the result by x in each iteration (this can be implemented efficiently as a bitwise shift left and an xor). The correctness of this method relies on the fact that the modulus polynomial is primitive (i.e., the smallest n such that the modulus polynomial divides \(x^n - 1\) is 255), and is not trivial to show in Coq.
Separately, although in the functional model we prove results for arbitrary fields and irreducible polynomials, here we need to show that several specific polynomials are irreducible and primitive (several field sizes are allowed by the code, although only one is used). Both of these conditions require showing that a polynomial is not divisible by a set of polynomials, so the easiest way to show this is by direct computation along with a proof that this computation is sufficient. However, MathComp polynomials are opaque and not computable (dividing two MathComp polynomials results in a hanging computation), so we needed to define concrete, computable polynomials and operations and relate them to their MathComp equivalents. Then, we can prove that the particular polynomials that the C code uses satisfy all needed properties.
6.5 Verifying 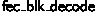
The function spec for  is quite long; it consists of many tedious preconditions to ensure that the input packets are stored correctly in memory, that the length and packet status arrays correspond to the actual packets in memory, and that the various integer parameters are within their correct bounds. The list of preconditions is long; however, these functions are called by client functions that do packet-handling and buffer management, and the verification of those functions will check that they do indeed set up their inputs correctly (see Sect. 8).
is quite long; it consists of many tedious preconditions to ensure that the input packets are stored correctly in memory, that the length and packet status arrays correspond to the actual packets in memory, and that the various integer parameters are within their correct bounds. The list of preconditions is long; however, these functions are called by client functions that do packet-handling and buffer management, and the verification of those functions will check that they do indeed set up their inputs correctly (see Sect. 8).
We focus on a key part of the spec: the precondition’s SEP clause includes the predicate  , which states that the Coq list
, which states that the Coq list  is stored in memory at the given pointers. In the postcondition’s SEP clause, this becomes
is stored in memory at the given pointers. In the postcondition’s SEP clause, this becomes  . In other words, after the function is run, the contents of the packet memory are represented by the low-level functional model of the decoder (the version that uses concrete types that VST can understand rather than opaque MathComp types).
. In other words, after the function is run, the contents of the packet memory are represented by the low-level functional model of the decoder (the version that uses concrete types that VST can understand rather than opaque MathComp types).
Our  theorem (Sect. 5.1) states that the high-level functional model correctly reconstructs the missing packets that were originally given to the encoder. Lemma
theorem (Sect. 5.1) states that the high-level functional model correctly reconstructs the missing packets that were originally given to the encoder. Lemma  lowers that result to the low-level functional model, using some injectivity results between the two models.
lowers that result to the low-level functional model, using some injectivity results between the two models.
Thus, a client of the code can compose the VST spec and the correctness theorem to prove that, after  is run, as long as the received packets and parities were correct, the missing data is recovered and the original data is now stored in memory (see Sect. 8).
is run, as long as the received packets and parities were correct, the missing data is recovered and the original data is now stored in memory (see Sect. 8).
6.6 Implementation Bug
While verifying  , we discovered a bug in the following code:
, we discovered a bug in the following code:

Here,  ranges from 0 to
ranges from 0 to  , and
, and  is a pointer to the input matrix. The problem is, when \(i=0\),
is a pointer to the input matrix. The problem is, when \(i=0\),  points to
points to  and thus
and thus  points to
points to  . By the C standard and the semantics of CompCert C, the comparison
. By the C standard and the semantics of CompCert C, the comparison  is undefined behavior. In fact, in C11, even the line
is undefined behavior. In fact, in C11, even the line  is undefined behavior [12, Section 6.5.6, #8].
is undefined behavior [12, Section 6.5.6, #8].
This may seem harmless, but 21st-century C compilers optimize under the assumption that the program does not exhibit undefined behavior. A compiler can assume that  cannot be reached when
cannot be reached when  , and it may mangle the loop body “knowing” that
, and it may mangle the loop body “knowing” that  . This has caused problems for systems code [26], and the solution is to avoid writing C programs with undefined behavior.
. This has caused problems for systems code [26], and the solution is to avoid writing C programs with undefined behavior.
Fortunately, VST’s machine-checked proof of soundness makes it impossible to prove a C program correct that contains undefined behavior (unless ruled out by a function precondition). The loop test  cannot be verified in VST, since undefined behavior cannot be ruled out.
cannot be verified in VST, since undefined behavior cannot be ruled out.
Without formal methods, this type of bug is quite difficult to find: it depends on subtle C semantics, today’s static analyzers won’t catch it,Footnote 2 and testing cannot catch it until (in some future year) an optimizing C compiler gets more aggressive. VST provides blanket assurance against this entire class of errors.
Moreover, because VST uses separation logic, we specify exactly what effects the code is allowed to have. Thus, in principle, this kind of verification is 100% resistant to adversarial attacks that try and put exploits into code provided that those exploits can be defined as a functional property of the C code (such as which memory addresses it accesses, what system calls it makes, etc.). But our methods cannot defend against side-channel attacks.
7 Related Work
Verification of Network Middleboxes. Through several recent efforts, verification of network functions running in the dataplane has become increasingly feasible. Software dataplane verification [9] uses symbolic execution to prove certain low-level properties (such as memory safety) about programs written with Click, a popular framework for configuring routers and writing network functions. Gravel [31] uses symbolic execution and SMT solvers to verify many middlebox-specific properties of Click programs, including functional correctness. VigNAT [30] uses a mix of symbolic execution and proof checking to verify a Network Address Translation (NAT) implementation in C; this approach requires the use of a specialized data structure library and annotations on the C program but is quite automated overall. Vigor [29] builds on VigNAT to extend similar methods to more general network function verification. It uses a simpler but less expressive specification language, enabling fully automatic verification. Vigor and VigNAT use Verifast [13], a separation-logic-based tool for verifying C programs that is more automated than VST but is not connected to a proof assistant; this makes functional model proofs much more difficult.
These tools are considerably more automated than our work, but face significant restrictions on the type of code they can verify: none can verify code with arbitrary unbounded loops, pointer arithmetic, or use of complex data structures. More importantly, none could handle the mathematical reasoning needed to prove the correctness of the functional model and ensure that the FEC correctly reconstructs packets. Verification of Error-Correcting Codes. Since error-correcting codes are both ubiquitous and quite complex to implement correctly, there has been a long line of research in formalizing various codes. Most of these efforts take the form of either automated hardware verification of digital circuits or recent efforts to create formalized libraries of error-correcting codes. We believe that our work is the first to connect a high-level, mathematical specification with an efficient implementation.
Error-correcting codes are hard to verify with automated methods such as model checking and BDDs because of the large state space and the complexity of the algorithms. Some recent efforts [8] have used automated hardware verification tools to verify (non-Reed-Solomon) ECCs, but they can handle very few bit errors. BLUEVERI [16] is a tool for verifying hardware implementations of finite field operations and was applied to Reed-Solomon codes. It can handle more errors (up to almost a dozen bits), but requires extensive manual effort and knowledge of hardware implementation details.
In a separate vein, several recently-developed libraries of formalized coding theory are similar to the functional model in our work, but are not connected to an efficient implementation. Most notably, Affeldt, Garrigue, and Saikawa have developed a Coq library for error-correcting codes, including Hamming and acyclic LDPC [1], Reed-Solomon [2], and BCH [3] codes. This library is built atop MathComp, and includes many theoretical results about each of these codes as well as specific encoders and decoders. Ideally, we would have liked to use this library as part of our functional model, but the implementation we verified differs significantly from standard Reed-Solomon coding, which corrects errors rather than erasures. Their library’s Euclidean-algorithm-based decoding is extremely different from the decoder in RSE.
In Lean, a coding theory library called Cotoleta was developed and used to prove results about Levenshtein distance [14] and Hamming(7,4) codes [11]. Separately, Hamming(7,4) and \(\frac{1}{2}\)-rate convolutional codes were verified in the ACL2 theorem prover [20] with a particular focus on correcting memory errors; these codes were verified against a particular memory model. Both of these projects focused on verifying concrete-sized codes; thus they did not require the same level of abstraction or general mathematical reasoning as our work.
8 Future Work
In a real system, the encoder and decoder verified in this work are called by clients who handle receiving packets, assigning them to batches, and maintaining various data structures. We are currently working to verify a real-world version of such a system. This will permit a single, clean, end-to-end correctness result; right now, we have separate results for the decoder’s correctness and the C program refinement which must be composed together. However, the specification of such a system introduces new challenges; it must reason about packet streams and network-specific features such as headers, timeouts, and packet reordering.
This C implementation of RSE has been useful in several projects at Bellcore/Telcordia/Peraton even though it cannot run at modern packet bit rates. We believe that a line-rate FPGA implementation of the finite-field matrix-multiply partial step is possible, and we are designing an API by which this could be controlled by a C program or a P4 program. Such an FPGA could be proved correct by a layered proof. The top layer would be our MathComp proof with no changes. The bottom layer could be proved using a Coq tool for hardware synthesis and functional-correctness verification, such as Kôika [7].
9 Conclusion
We have presented an efficient, real-world C implementation of Reed-Solomon forward erasure correction that we formally verified using the Coq proof assistant and the Verified Software Toolchain. The code was verified with only minor changes; one macro was turned into a function for ease of verification and one bug that caused undefined behavior was fixed. While the code has been in use for over 25 years, the correctness of certain parts of the underlying algorithm, a modified form of Reed-Solomon erasure coding, were still ill-understood, including a very restricted form of Gaussian elimination. We were able to use Coq’s Mathematical Components library to completely verify the correctness of this algorithm and VST to prove that the C code, with its various optimizations and modifications, correctly implements this algorithm. This demonstrates that tools like VST allow us to verify real-world, dusty-deck programs in C, even those whose correctness depends on a broad base of mathematics and those with numerous low-level optimizations. We believe this can be a viable approach to connect efficient low-level code with sophisticated high-level reasoning, enabling reliable software components for networks and other systems.
Notes
- 1.
Our Coq proofs and an appendix with expanded definitions, specs, and proofs can be found at github.com/verified-network-toolchain/Verified-FEC/tree/cav22.
- 2.
“Conceptually, this undefined-behavior optimization bug is possible to trigger with STACK’s approach [26]. But, as for the current implementation of STACK, the answer is likely no, because it depends on LLVM to do loop unrolling/inlining ...and I doubt LLVM would do either ....” (Xi Wang, e-mail of May 23, 2022).
References
Affeldt, R., Garrigue, J.: Formalization of error-correcting codes: from Hamming to modern coding theory. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 17–33. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22102-1_2
Affeldt, R., Garrigue, J., Saikawa, T.: Formalization of Reed-Solomon codes and progress report on formalization of LDPC codes. In: 2016 International Symposium on Information Theory and Its Applications (ISITA), pp. 532–536 (2016)
Affeldt, R., Garrigue, J., Saikawa, T.: A library for formalization of linear error-correcting codes. J. Autom. Reason. 64(6), 1123–1164 (2020). https://doi.org/10.1007/s10817-019-09538-8
Appel, A.W.: Verification of a cryptographic primitive: SHA-256. ACM Trans. Program. Lang. Syst. 37(2), 1–31 (2015). https://doi.org/10.1145/2701415
Appel, A.W., Bertot, Y.: C floating-point proofs layered with VST and Flocq. J. Formaliz. Reason. 13(1), 1–16 (2020). https://doi.org/10.6092/issn.1972-5787/11442
Appel, A.W., et al.: Program Logics for Certified Compilers. Cambridge University Press, Cambridge (2014)
Bourgeat, T., Pit-Claudel, C., Chlipala, A.: The essence of Bluespec: a core language for rule-based hardware design. In: PLDI’20: Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 243–257 (2020)
Devarajegowda, K., Servadei, L., Han, Z., Werner, M., Ecker, W.: Formal verification methodology in an industrial setup. In: 2019 22nd Euromicro Conference on Digital System Design (DSD), pp. 610–614 (2019). https://doi.org/10.1109/DSD.2019.00094
Dobrescu, M., Argyraki, K.: Software dataplane verification. In: 11th USENIX Symposium on Networked Systems Design and Implementation (NSDI 14), pp. 101–114. USENIX Association, Seattle, April 2014
Gonthier, G., Mahboubi, A., Tassi, E.: A Small Scale Reflection Extension for the Coq system. Research Report RR-6455, Inria Saclay Ile de France (2015). https://hal.inria.fr/inria-00258384
Hagiwara, M., Nakano, K., Kong, J.: Formalization of coding theory using lean. In: 2016 International Symposium on Information Theory and Its Applications (ISITA), pp. 522–526 (2016)
ISO: ISO/IEC 9899:2011 Information technology – Programming languages – C, December 2011. http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1548.pdf
Jacobs, B., Piessens, F.: The VeriFast program verifier (2008)
Kong, J., Webb, D.J., Hagiwara, M.: Formalization of insertion/deletion codes and the Levenshtein metric in lean. In: 2018 International Symposium on Information Theory and Its Applications (ISITA), pp. 11–15 (2018)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009). https://doi.org/10.1145/1538788.1538814
Lvov, A., Lastras-Montaño, L.A., Paruthi, V., Shadowen, R., El-Zein, A.: Formal verification of error correcting circuits using computational algebraic geometry. In: 2012 Formal Methods in Computer-Aided Design (FMCAD), pp. 141–148 (2012)
Mansky, W., Honoré, W., Appel, A.W.: Connecting higher-order separation logic to a first-order outside world. In: ESOP 2020. LNCS, vol. 12075, pp. 428–455. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-44914-8_16
McAuley, A.J.: Reliable broadband communication using a burst erasure correcting code. In: Proceedings of the ACM Symposium on Communications Architectures & Protocols, SIGCOMM 1990, New York, NY, USA, pp. 297–306 (1990). https://doi.org/10.1145/99508.99566
McAuley, A.J.: Forward error correction code system. U.S. Patent 5,115,436 (1992)
Naseer, M., Ahmad, W., Hasan, O.: Formal verification of ECCs for memories using ACL2. J. Electron. Test. 36(5), 643–663 (2020). https://doi.org/10.1007/s10836-020-05904-2
Plank, J.S.: A tutorial on Reed-Solomon coding for fault-tolerance in RAID-like systems. Softw. Pract. Exp. 27(9), 995–1012 (1997)
Preparata, F.P.: Holographic dispersal and recovery of information. IEEE Trans. Inf. Theory 35(5), 1123–1124 (2006). https://doi.org/10.1109/18.42233
Rabin, M.O.: Efficient dispersal of information for security, load balancing, and fault tolerance. J. ACM 36(2), 335–348 (1989). https://doi.org/10.1145/62044.62050
Reed, I.S., Solomon, G.: Polynomial codes over certain finite fields. J. Soc. Ind. Appl. Math. 8, 300–304 (1960)
Schwarz, T., Buckhard, W.: RAID organization and performance. In: [1992] Proceedings of the 12th International Conference on Distributed Computing Systems, pp. 318–325 (1992). https://doi.org/10.1109/ICDCS.1992.235025
Wang, X., Zeldovich, N., Kaashoek, M.F., Solar-Lezama, A.: Towards optimization-safe systems: analyzing the impact of undefined behavior. In: Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles, SOSP 2013, pp. 260–275. Association for Computing Machinery (2013). https://doi.org/10.1145/2517349.2522728
Wicker, S.B., Bhargava, V.K.: Reed-Solomon Codes and Their Applications. Wiley-IEEE Press (1999)
Ye, K.Q., Green, M., Sanguansin, N., Beringer, L., Petcher, A., Appel, A.W.: Verified correctness and security of mbedTLS HMAC-DRBG. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, New York, NY, USA, pp. 2007–2020 (2017). https://doi.org/10.1145/3133956.3133974
Zaostrovnykh, A., et al.: Verifying software network functions with no verification expertise. In: Proceedings of the 27th ACM Symposium on Operating Systems Principles, SOSP 2019, New York, NY, USA, pp. 275–290 (2019). https://doi.org/10.1145/3341301.3359647
Zaostrovnykh, A., Pirelli, S., Pedrosa, L., Argyraki, K., Candea, G.: A formally verified NAT. In: Proceedings of the Conference of the ACM Special Interest Group on Data Communication, SIGCOMM 2017, New York, NY, USA, pp. 141–154 (2017). https://doi.org/10.1145/3098822.3098833
Zhang, K., Zhuo, D., Akella, A., Krishnamurthy, A., Wang, X.: Automated verification of customizable middlebox properties with Gravel. In: 17th USENIX Symposium on Networked Systems Design and Implementation (NSDI 20), pp. 221–239. USENIX Association, Santa Clara, CA, February 2020. https://www.usenix.org/conference/nsdi20/presentation/zhang-kaiyuan
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
The appendix to this paper can be found in our git repo (see footnote 1) in doc/Appendix.pdf.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Cohen, J.M., Wang, Q., Appel, A.W. (2022). Verified Erasure Correction in Coq with MathComp and VST. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13372. Springer, Cham. https://doi.org/10.1007/978-3-031-13188-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-031-13188-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13187-5
Online ISBN: 978-3-031-13188-2
eBook Packages: Computer ScienceComputer Science (R0)




 is equal to storing a 1D array containing
is equal to storing a 1D array containing 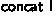 , all of the inner lists of
, all of the inner lists of 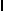 concatenated together. This lemma is generic and will be added to VST for future use. For dealing with arrays of pointers, we used VST’s
concatenated together. This lemma is generic and will be added to VST for future use. For dealing with arrays of pointers, we used VST’s 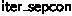 , which represents iterated separating conjunction over a collection of predicates, and we proved lemmas allowing us to extract and modify a single element of the collection. Additionally, we needed several smaller lemmas and tactics for handling the resulting pointer-equality proof obligations arising from these type conversions and for simplifying the pointer comparisons in loop guards, which we plan to contribute to VST in order to improve the handling of pointer arithmetic.
, which represents iterated separating conjunction over a collection of predicates, and we proved lemmas allowing us to extract and modify a single element of the collection. Additionally, we needed several smaller lemmas and tactics for handling the resulting pointer-equality proof obligations arising from these type conversions and for simplifying the pointer comparisons in loop guards, which we plan to contribute to VST in order to improve the handling of pointer arithmetic.