Abstract
We propose generalizations of reduction pairs, well-established techniques for proving termination of term rewriting, in order to prove unsatisfiability of reachability (infeasibility) in plain and conditional term rewriting. We adapt the weighted path order, a merger of the Knuth–Bendix order and the lexicographic path order, into the proposed framework. The proposed approach is implemented in the termination prover NaTT, and the strength of our approach is demonstrated through examples and experiments.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In the research area of term rewriting, among the most well-studied topics are termination, confluence, and reachability analyses.
In termination analysis, a crucial task used to be to design reduction orders, well-founded orderings over terms that are closed under contexts and substitutions. Well-known examples of such orderings include the Knuth–Bendix ordering [14], polynomial interpretations [18], multiset/lexicographic path ordering [4, 13], and matrix interpretations [5]. The dependency pair framework generalized reduction orders into reduction pairs [2, 9, 12], and there are a number of implementations that automatically find reduction pairs, e.g., AProVE [7],
 [16], MU-TERM [11], NaTT [35], competing in the International Termination Competition [8].
[16], MU-TERM [11], NaTT [35], competing in the International Termination Competition [8].
Traditional reachability analysis (cf. [6]) has been concerned with the possibility of rewriting a given source term s to a target t, where variables in the terms are treated as constants. There is an increasing need for solving a more general question: is it possible to instantiate variables so that the instance of s rewrites to the instance of t? Let us illustrate the problem with an elementary example.
Example 1
Consider the following TRS encoding addition of natural numbers:

The reachability constraint  represents the possibility of rewriting from
represents the possibility of rewriting from  to
to  , where variables
, where variables  and
and  can be arbitrary terms.
can be arbitrary terms.
This (un)satisfiability problem of reachability, also called (in)feasibility, plays important roles in termination [24] and confluence analyses of (conditional) rewriting [21]. A tool competition dedicated for this problem has been founded as the infeasibility (INF) category in the International Confluence Competition (CoCo) since 2019 [25].
In this paper, we propose a new method for proving unsatisfiability of reachability, using the term ordering techniques developed for termination analysis. Specifically, in Sect. 3, we first generalize reduction pairs to rewrite pairs, and show that they can be used for proving unsatisfiability of reachability. We further generalize the notion to co-rewrite pairs, yielding a sound and complete method. The power of the proposed method is demonstrated by importing (relaxed) semantic term orderings from termination analysis.
In order to import also syntactic term orderings, in Sect. 4 we identify a condition when the weighted path order (WPO) [36] forms a rewrite pair. Since KBO and LPO are instances of WPO, we see that these orderings can also be used in our method. In Sect. 5 we also present how to derive co-rewrite pairs from WPO.
In Sect. 6, we adapt the approach into conditional rewriting. Section 7 reports on the implementation and experiments conducted on examples in the paper and the benchmark set of CoCo 2021.
Related Work Our rewrite pairs are essentially Aoto’s discrimination pairs [1] which are closed under substitutions. On way of disproving confluence, Aoto introduced discrimination pairs and used them in proving non-joinability. The joinability of terms s and t is expressed as \(\exists u.\ s \rightarrow _\mathcal {R}^* u \leftarrow _\mathcal {R}^* t\), while the current paper is concerned with \(\exists \theta .\ s\theta \rightarrow _\mathcal {R}^* t\theta \). As substitutions are not considered, discrimination pairs do not need closure under substitutions, and Aoto’s insights are mainly for dealing with the reverse rewriting \(\leftarrow _\mathcal {R}^*\).
Lucas and Gutiérrez [19] proposed reducing infeasibility to the model finding of first-order logic. Our formulations especially in Sect. 6 are similar to theirs. A crucial difference is that, while they encode the closure properties and order properties into logical formulas and delegate these tasks to the background theory solvers, we ensure these properties by means of reduction pairs, for which well-established techniques exist in the literature.
Sternagel and Yamada [30] proposed a framework for analyzing reachability by combining basic logical manipulations, and Gutiérrez and Lucas [10] proposed another framework, similar to the dependency pair framework. The present work focuses on atomic analysis techniques, and is orthogonal to these efforts of combining techniques.
2 Preliminaries
We assume familiarity with term rewriting, cf. [3] or [32]. For a binary relation denoted by a symbol like \(\sqsupset \), we denote its dual relation by \(\sqsubset \) and the negated relation by \(\not \sqsupset \). Relation composition is denoted by \(\circ \).
Throughout the paper we fix a set \(\mathcal {V}\) of variable symbols. A signature is a set \(\mathcal {F}\) of function symbols, where each \(f\in \mathcal {F}\) is associated with its arity, the number of arguments. The set of terms built from \(\mathcal {F}\) and \(\mathcal {V}\) is denoted by \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), where a term is either in \(\mathcal {V}\) or of form \(f(s_1,\dots ,s_n)\) where \(f \in \mathcal {F}\) is n-ary and \(s_1,\dots ,s_n \in \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \). Given a term \(s\in \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \) and a substitution \(\theta : \mathcal {V}\rightarrow \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), \(s\theta \) denotes the term obtained from s by replacing every variable x by \(\theta (x)\). A context is a term  where a special variable
where a special variable  occurs exactly once. Given \(s\in \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), we denote by C[s] the term obtained by replacing
occurs exactly once. Given \(s\in \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), we denote by C[s] the term obtained by replacing  by s in C.
by s in C.
A relation \(\sqsupset \) over terms is closed under substitutions (resp. contexts) iff \(s \sqsupset t\) implies \(s\theta \sqsupset t\theta \) for any substitution \(\theta \) (resp. \(C[s] \sqsupset C[t]\) for any context C). Relations over terms that are closed under contexts and substitutions are called rewrite relations. Rewrite relations which are also preorders are called rewrite preorders, and those which are strict orders are rewrite orders. Well-founded rewrite orders are called reduction orders.
A term rewrite system (TRS) \(\mathcal {R}\) is a (usually finite) relation over terms, where each \(\langle l,r\rangle \in \mathcal {R}\) is called a rewrite rule and written \(l \rightarrow r\). We do not require the usual assumption that \(l \notin \mathcal {V}\) and variables occurring in r must occur in l. The rewrite step \(\rightarrow _\mathcal {R}\) induced by TRS \(\mathcal {R}\) is the least rewrite relation containing \(\mathcal {R}\). Its reflexive transitive closure is denoted by \(\rightarrow _\mathcal {R}^*\), which is the least rewrite preorder containing \(\mathcal {R}\).
A reachability atom is a pair of terms s and t, written \(s \twoheadrightarrow t\). We say that \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-satisfiable iff \(s\theta \rightarrow _\mathcal {R}^* t\theta \) for some \(\theta \), and \(\mathcal {R}\)-unsatisfiable otherwise.
3 Term Orderings for Non-reachability
Reduction pairs constitute the core ingredient in proving termination with dependency pairs. Just as rewrite orders generalize reduction orders, we first introduce the notion of “rewrite pairs” by removing the well-foundedness assumption of reduction pairs.
Definition 1
(rewrite pair). We call a pair \(\langle \sqsupseteq ,\sqsupset \rangle \) of relations an order pair if \(\sqsupseteq \) is a preorder, \({\sqsupset }\) is irreflexive, \({\sqsupset } \subseteq {\sqsupseteq }\), and \({\sqsupseteq }\circ {\sqsupset }\circ {\sqsupseteq } \subseteq {\sqsupset }\). A rewrite pair is an order pair \(\langle \sqsupseteq ,\sqsupset \rangle \) over terms such that both \(\sqsupseteq \) and \(\sqsupset \) are closed under substitutions and \(\sqsupseteq \) is closed under contexts. It is called a reduction pair if moreover \(\sqsupset \) is well-founded.
Standard definitions of reduction pairs put less order-like assumptions than the above definition, but the above (more natural) assumptions do not lose the generality of previous definitions [34]. Due to these assumptions, our rewrite pair satisfies the assumption of discrimination pairs [1].
The following statement is our first observation: a rewrite pair can prove non-reachability.
Theorem 1
If \(\langle \sqsupseteq ,\sqsupset \rangle \) is a rewrite pair, \(\mathcal {R}\subseteq {\sqsupseteq }\) and \(s \sqsubset t\), then \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable.
A similar observation has been made [20, Theorem 11], where well-foundedness is assumed instead of irreflexivity. Note that irreflexivity is essential: if \(s \sqsubset s\) for some s, then we have \(s \sqsubset s\) but \(s \twoheadrightarrow s\) is \(\mathcal {R}\)-satisfiable.
The proof of Theorem 1 will be postponed until more general Theorem 2 will be obtained. Instead, we start with utilizing Theorem 1 by generalizing a classical way of defining reduction pairs: the semantic approach [23].
Definition 2
(model). An \(\mathcal {F}\)-algebra \(\mathcal {A}= \langle A,[\cdot ]_{}\rangle \) specifies a set A called the carrier and an interpretation \([f]_{} : A^n \rightarrow A\) to each n-ary \(f \in \mathcal {F}\). The evaluation of a term s under assignment \(\alpha : \mathcal {V}\rightarrow A\) is defined as usual and denoted by \([s]_{}\alpha \).
A related/preordered \(\mathcal {F}\)-algebra \(\langle \mathcal {A},\sqsupset \rangle = \langle A,[\cdot ]_{},\sqsupset \rangle \) consists of an \(\mathcal {F}\)-algebra and a relation/preorder \(\sqsupset \) on A. Given \(\alpha : \mathcal {V}\rightarrow A\), we write \([s \sqsupset t]_{}\alpha \) to mean \([s]_{}\alpha \sqsupset [t]_{}\alpha \). We write \(\mathcal {A}\models s \sqsupset t\) if \([s \sqsupset t]_{}\alpha \) holds for every \(\alpha : \mathcal {V}\rightarrow A\). We say \(\langle \mathcal {A},\sqsupset \rangle \) is a (relational) model of a TRS \(\mathcal {R}\) if \(\mathcal {A}\models l \sqsupset r\) for every \(l\rightarrow r \in \mathcal {R}\). We say \(\langle \mathcal {A},\sqsupset \rangle \) is monotone if \(a_i \sqsupset a_i'\) implies \( [f]_{}(a_1,\dots ,a_i,\dots ,a_n) \sqsupset [f]_{}(a_1,\dots ,a_i',\dots ,a_n) \) for arbitrary \(a_1,\dots ,a_n,a_i' \in A\) and n-ary \(f\in \mathcal {F}\).
The notion of relational models is due to van Oostrom [28]. In this paper, we simply call them models. Models in terms of equational theory are models \(\langle \mathcal {A},=\rangle \) in the above definition, where monotonicity is inherent. Quasi-models of Zantema [37] are preordered (or partially ordered) monotone models. Theorem 1 can be reformulated in the semantic manner as follows:
Corollary 1
If \(\langle \ge ,>\rangle \) is an order pair, \(\langle \mathcal {A},\ge \rangle \) is a monotone model of \(\mathcal {R}\), and \(\mathcal {A}\models s < t\), then \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable.
Note that Corollary 1 does not demand well-foundedness on >. In particular, one can employ models over negative numbers (or equivalently, positive numbers with the order pair \(\langle \le ,<\rangle \)).
Example 2
Consider again the TRS  of Example 1. The monotone ordered \(\mathcal {F}\)-algebra \(\langle \mathbb {Z}_{\le 0},[\cdot ]_{},\ge \rangle \) defined by
of Example 1. The monotone ordered \(\mathcal {F}\)-algebra \(\langle \mathbb {Z}_{\le 0},[\cdot ]_{},\ge \rangle \) defined by

is a model of  : Whenever \(x,y \in \mathbb {Z}_{\le 0}\), we have
: Whenever \(x,y \in \mathbb {Z}_{\le 0}\), we have

Now we can conclude that the reachability constraint  is
is  -unsatisfiable by
-unsatisfiable by  : Whenever \(x,y \in \mathbb {Z}_{\le 0}\), we have
: Whenever \(x,y \in \mathbb {Z}_{\le 0}\), we have

Observe that in Theorem 1, \(\sqsupset \) occurs only in the dual form \(\sqsubset \). Hence we now directly analyze the condition which \(\sqsupseteq \) and \(\sqsubset \) should satisfy to prove non-reachability, and this gives a sound and complete method.
Definition 3
(co-rewrite pair). We call a pair \(\langle \sqsupseteq ,\sqsubset \rangle \) of relations over terms a co-rewrite pair, if \(\sqsupseteq \) is a rewrite preorder, \(\sqsubset \) is closed under substitutions, and \({\sqsupseteq } \cap {\sqsubset } = \emptyset \).
Theorem 2
\(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable if and only if there exists a co-rewrite pair \(\langle \sqsupseteq ,\sqsubset \rangle \) such that \(\mathcal {R}\subseteq {\sqsupseteq }\) and \(s \sqsubset t\).
Proof
For the “if” direction, suppose on the contrary that \(s\theta \rightarrow _\mathcal {R}^* t\theta \) for some \(\theta \). Since \(\sqsupseteq \) is a rewrite preorder containing \(\mathcal {R}\) and \(\rightarrow _\mathcal {R}^*\) is the least of such, we must have \(s\theta \sqsupseteq t\theta \). On the other hand, since \(s \sqsubset t\) and \(\sqsubset \) is closed under substitutions, we have \(s\theta \sqsubset t\theta \). This is not possible since \({\sqsupseteq }\cup {\sqsubset } = \emptyset \).
For the “only if” direction, take \(\rightarrow _\mathcal {R}^*\) as \(\sqsupseteq \) and define \(\sqsubset \) by \(s \sqsubset t\) iff \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable. Then clearly \(\sqsubset \) is closed under substitutions, \({\rightarrow _\mathcal {R}^*} \cap {\sqsubset } = \emptyset \), and \(\mathcal {R}\subseteq {\rightarrow _\mathcal {R}^*}\). \(\square \)
Theorem 2 can be more concisely reformulated in the model-oriented manner, as the greatest choice of \(\sqsubset \) can be specified: \(s \sqsubset t\) iff \(\mathcal {A}\models s \ngeq t\).
Corollary 2
\(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable if and only if there exists a monotone preordered model \(\langle \mathcal {A},\ge \rangle \) of \(\mathcal {R}\) such that \(\mathcal {A}\models s \ngeq t\).
Corollary 2 is useful when models over non-totally ordered carriers are considered. There are important methods (for termination) that crucially rely on such carriers: the matrix interpretations [5], or more generally the tuple interpretations [15, 34].
Example 3
Consider the following TRS, where the first rule is from [5]:

The preordered  -algebra \(\langle \mathbb {N}^2, [\cdot ]_{},\ge \rangle \) defined by
-algebra \(\langle \mathbb {N}^2, [\cdot ]_{},\ge \rangle \) defined by

is a model of \(\mathcal {R}_{mat}\), where \(\ge \) is extended pointwise over \(\mathbb {N}^2\). Indeed, the first rule is oriented as the following calculation demonstrates:

and the second rule can be easily checked. Now we prove that  is \(\mathcal {R}_{mat}\)-unsatisfiable by Corollary 2. Indeed,
is \(\mathcal {R}_{mat}\)-unsatisfiable by Corollary 2. Indeed,  is shown as follows:
is shown as follows:

for any \(x, y \in \mathbb {N}\). Note also that Theorem 1 is not applicable, since  due to the second coordinate.
due to the second coordinate.
We conclude the section by proving Theorem 1 via Theorem 2.
Proof
(of Theorem 1). We show that \(\langle \sqsupseteq ,\sqsubset \rangle \) form a co-rewrite pair when \(\langle \sqsupseteq ,\sqsupset \rangle \) is a rewrite pair. It suffices to show that \({\sqsupseteq } \cap {\sqsubset } = \emptyset \). To this end, suppose on the contrary that \(s \sqsupseteq t \sqsupset s\). By compatibility, we have \(s \sqsupset s\), which contradicts the irreflexivity of \(\sqsupset \). \(\square \)
4 Weighted Path Order for Non-reachability
The previous section was concerned with the semantic approach towards obtaining (co-)rewrite pairs. In this section we focus on the syntactic approach. We choose the weighted path order (WPO), which subsumes both the lexicographic path order (LPO) and the Knuth-Bendix order (KBO), so the result of this section applies to these more well-known methods. The multiset path order [4] can also be subsumed [29], but we omit this extension to keep the presentation simple. WPO is induced by three ingredients: an \(\mathcal {F}\)-algebra; a precedence ordering over function symbols; and a (partial) status, which controls the recursive behavior of the ordering.
Definition 4
(partial status). A partial status \(\pi \) specifies for each n-ary \(f \in \mathcal {F}\) a list \(\pi (f) \in \{1,\dots ,n\}^*\), also seen as a set, of its argument positions. We say \(\pi \) is total if \(1,\dots ,n \in \pi (f)\) whenever f is n-ary. When \(\pi (f) = [i_1,\dots ,i_m]\), we denote \([s_{i_1},\dots ,s_{i_m}]\) by \(\pi _f(s_1,\dots ,s_n)\).
For instance, the empty status \(\pi (f) = [\,]\) allows WPO to subsume weakly monotone interpretations [36, Section 4.1]. We allow positions to be duplicated, following [33].
Definition 5
(WPO [36]). Let \(\pi \) be a partial status, \(\mathcal {A}\) an \(\mathcal {F}\)-algebra, and \(\langle \ge ,>\rangle \) and \(\langle \succsim ,\succ \rangle \) be pairs of relations on \(\mathcal {A}\) and \(\mathcal {F}\), respectively. The weighted path order \(\mathsf {WPO}(\pi ,\mathcal {A},\ge ,>,\succsim ,\succ )\), or \(\mathsf {WPO}(\mathcal {A})\) or even \(\mathsf {WPO}\) for short, is the pair \(\langle \sqsupseteq _\mathsf {WPO},\sqsupset _\mathsf {WPO}\rangle \) of relations over terms defined as follows: \(s \sqsupset _\mathsf {WPO}t\) iff
-
1.
\(\mathcal {A}\models s > t\) or
-
2.
\(\mathcal {A}\models s \ge t\) and
-
(a)
 , \(s_i \sqsupseteq _\mathsf {WPO}t\) for some \(i \in \pi (f)\);
, \(s_i \sqsupseteq _\mathsf {WPO}t\) for some \(i \in \pi (f)\); -
(b)
 , \(t = g(t_1,\dots ,t_m)\), \(s \sqsupset _\mathsf {WPO}t_j\) for every \(j \in \pi (g)\) and
, \(t = g(t_1,\dots ,t_m)\), \(s \sqsupset _\mathsf {WPO}t_j\) for every \(j \in \pi (g)\) and -
i.
\(f \succ g\), or
-
ii.
\(f \succsim g\) and
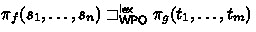 .
.
-
i.
-
(a)
The relation \(\sqsupseteq _\mathsf {WPO}\) is defined similarly, but with \(\sqsupseteq _\mathsf {WPO}^\mathsf {lex}\) instead of \(\sqsupset _\mathsf {WPO}^\mathsf {lex}\) in (2b-ii) and the following subcase is added in case 2:
-
(c)
\(s = t \in \mathcal {V}\).
Here \(\langle \sqsupseteq _{P}^\mathsf {lex},\sqsupset _{P}^\mathsf {lex}\rangle \) denotes the lexicographic extension of a pair \(P = \langle \sqsupseteq _P,\sqsupset _P\rangle \) of relations, defined by:  iff
iff
-
\(m = 0\) and
 , or
, or -
\(m, n > 0\) and \(s_1 > t_1\) or both
 and
and  .
.
LPO is \(\mathsf {WPO}\) induced by a total status \(\pi \) and a trivial \(\mathcal {F}\)-algebra as \(\mathcal {A}\), and is written \(\mathsf {LPO}\). Allowing partial statuses corresponds to applying argument filters [2, 17] (except for collapsing ones). KBO is a special case of WPO where \(\pi \) is total and \(\mathcal {A}\) is induced by an admissible weight function.
For termination analysis, a precondition for \(\mathsf {WPO}\) to be a reduction pair is crucial. In this work, we only need it to be a rewrite pair; that is, well-foundedness is not necessary. Thus, for instance, it is possible to have \(x \sqsupset _\mathsf {WPO}f(x)\) by \([f]_{}(x) = x - 1\). This explains why \(s \in \mathcal {V}\) is permitted in case 1, which might look useless to those who are already familiar with termination analysis.
We formulate the main claim of this section as follows.
Definition 6
(\(\pi \)-simplicity). We say a related \(\mathcal {F}\)-algebra \(\langle A,[\cdot ]_{},\ge \rangle \) is \(\pi \)-simpleFootnote 1 for a partial status \(\pi \) iff \([f]_{}(a_1,\dots ,a_n) \ge a_i\) for arbitrary n-ary \(f \in \mathcal {F}\), \(a_1,\dots ,a_n \in A\), and \(i \in \pi (f)\).
Proposition 1
If \(\langle \ge ,>\rangle \) and \(\langle \succsim ,\succ \rangle \) are order pairs on \(\mathcal {A}\) and \(\mathcal {F}\), and \(\langle \mathcal {A},\ge \rangle \) is monotone and \(\pi \)-simple, then \(\langle \sqsupseteq _\mathsf {WPO},\sqsupset _\mathsf {WPO}\rangle \) is a rewrite pair.
Under these conditions, it is known that \(\sqsupseteq _\mathsf {WPO}\) is closed under contexts and \(\sqsupset _\mathsf {WPO}\) is compatible with \(\sqsupseteq _\mathsf {WPO}\) [36, Lemmas 7, 10, 13]. Later in this section we prove other properties necessary for Proposition 1, for which the claims in [36] must be generalized for the purpose of this paper.
The benefit of having syntax-aware methods can be easily observed by recalling why we have them in termination analysis.
Example 4
([13]). Consider the TRS  consisting of the following rules:
consisting of the following rules:

and suppose that a monotone  -algebra \(\langle \mathbb {N},[\cdot ]_{},\ge \rangle \) is a model of
-algebra \(\langle \mathbb {N},[\cdot ]_{},\ge \rangle \) is a model of  . Then, denoting the Ackermann function by A, we have
. Then, denoting the Ackermann function by A, we have

Now consider proving the obvious fact that  is
is  -unsatisfiable. This requires
-unsatisfiable. This requires  , and then
, and then  by an inductive argument. This is not possible if
by an inductive argument. This is not possible if  is primitive recursive (e.g., a polynomial), since (1) with
is primitive recursive (e.g., a polynomial), since (1) with  contradicts the well-known fact that the Ackermann function has no primitive-recursive bound.
contradicts the well-known fact that the Ackermann function has no primitive-recursive bound.
On the other hand, \(\mathsf {LPO}\) with  satisfies
satisfies  (\(\subseteq {\sqsupseteq _\mathsf {LPO}}\)) and
(\(\subseteq {\sqsupseteq _\mathsf {LPO}}\)) and  . Thus Theorem 1 with \(\langle \sqsupseteq ,\sqsupset \rangle = \langle \sqsupseteq _\mathsf {LPO},\sqsupset _\mathsf {LPO}\rangle \) proves that
. Thus Theorem 1 with \(\langle \sqsupseteq ,\sqsupset \rangle = \langle \sqsupseteq _\mathsf {LPO},\sqsupset _\mathsf {LPO}\rangle \) proves that  is
is  -unsatisfiable, thanks to Proposition 1 and Theorem 1.
-unsatisfiable, thanks to Proposition 1 and Theorem 1.
Example 5
Consider the TRS consisting of the following rules:

\(\mathsf {WPO}\) (or KBO) induced by \(\mathcal {A}= \langle \mathbb {N},[\cdot ]_{}\rangle \) and precedence \(\langle \succsim ,\succ \rangle \) such that

satisfies \(\mathcal {R}_{kbo} \subseteq {\sqsupseteq _\mathsf {WPO}}\). Thus, for instance  is \(\mathcal {R}_{kbo}\)-unsatisfiable by Theorem 1. On the other hand, let \(\langle A,[\cdot ]_{},\ge \rangle \) with \(A \subseteq \mathbb {Z}\) be a model of \(\mathcal {R}_{kbo}\). Using the idea of [38, Proposition 11], one can show
is \(\mathcal {R}_{kbo}\)-unsatisfiable by Theorem 1. On the other hand, let \(\langle A,[\cdot ]_{},\ge \rangle \) with \(A \subseteq \mathbb {Z}\) be a model of \(\mathcal {R}_{kbo}\). Using the idea of [38, Proposition 11], one can show  . Hence, Corollary 2 with models over a subset of integers cannot handle the problem. LPO orients the first rule from right to left and hence cannot handle the problem either.
. Hence, Corollary 2 with models over a subset of integers cannot handle the problem. LPO orients the first rule from right to left and hence cannot handle the problem either.
The power of \(\mathsf {WPO}\) can also be easily verified, by considering

By extending the above \(\mathsf {WPO}\) with  and
and  , which does not fall into the class of KBO anymore,Footnote 2 we can prove, e.g., that
, which does not fall into the class of KBO anymore,Footnote 2 we can prove, e.g., that  is \(\mathcal {R}\)-unsatisfiable. None of the above mentioned methods can handle this problem.
is \(\mathcal {R}\)-unsatisfiable. None of the above mentioned methods can handle this problem.
The rest of this section is dedicated for proving Proposition 1. Similar results are present in [36], but they make implicit assumptions such as that \(\ge \) and \(\succsim \) are preorders. In this paper we need more essential assumptions as we will consider non-transitive relations in the next section.
First we reprove the reflexivity of \(\sqsupseteq _\mathsf {WPO}\). The proof also serves as a basis for the more complicated irreflexivity proof.
Lemma 1
If both \(\ge \) and \(\succsim \) are reflexive and \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple, then
-
1.
\(i \in \pi (f)\) implies \(f(s_1,\dots ,s_n) \sqsupset _\mathsf {WPO}s_i\), and
-
2.
\(s \sqsupseteq _\mathsf {WPO}s\), i.e., \(\sqsupseteq _\mathsf {WPO}\) is reflexive.
Proof
As \(s \sqsupseteq _\mathsf {WPO}s\) is trivial when \(s \in \mathcal {V}\), we assume \(s = f(s_1,\dots ,s_n)\) and prove the two claims by induction on the structure of s. For the first claim, by \(\pi \)-simplicity, for any \(\alpha \) we have \([s]_{}\alpha = [f]_{}([s_1]_{}\alpha ,\dots ,[s_n]_{}\alpha ) \ge [s_i]_{}\alpha \), and hence \(\mathcal {A}\models s \ge s_i\). By the second claim of induction hypothesis we have \(s_i \sqsupseteq _\mathsf {WPO}s_i\), and thus \(s \sqsupset _\mathsf {WPO}s_i\) follows by (2a) of Definition 5. Next we show \(s \sqsupseteq _\mathsf {WPO}s\) holds by (2b-ii). Indeed, \(\mathcal {A}\models s \ge s\) follows from the reflexivity of \(\ge \); \(s \sqsupset _\mathsf {WPO}s_i\) for every \(i \in \pi (f)\) as shown above; \(f \succsim f\) as \(\succsim \) is reflexive; and finally,  is due to induction hypothesis and the fact that lexicographic extension preserves reflexivity. \(\square \)
is due to induction hypothesis and the fact that lexicographic extension preserves reflexivity. \(\square \)
Using reflexivity, we can show that both \(\sqsupseteq _\mathsf {WPO}\) and \(\sqsupset _\mathsf {WPO}\) are closed under substitutions. This result will be reused in Sect. 5, where it will be essential that neither \(\ge \) nor > need be transitive.
Lemma 2
If both \(\ge \) and \(\succsim \) are reflexive and \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple, then both \(\sqsupseteq _\mathsf {WPO}\) and \(\sqsupset _\mathsf {WPO}\) are closed under substitutions.
Proof
We prove by induction on s and t that \(s \sqsupseteq _\mathsf {WPO}t\) implies \(s\theta \sqsupseteq _\mathsf {WPO}t\theta \) and that \(s \sqsupset _\mathsf {WPO}t\) implies \(s\theta \sqsupset _\mathsf {WPO}t\theta \). We prove the first claim by case analysis on how \(s \sqsupseteq _\mathsf {WPO}t\) is derived. The other claim is analogous, without case (2c) below.
-
1.
\(\mathcal {A}\models s > t\): Then we have \(\mathcal {A}\models s\theta > t\theta \) and thus \(s\theta \sqsupset _\mathsf {WPO}t\theta \) by case 1.
-
2.
\(\mathcal {A}\models s \ge t\): Then we have \(\mathcal {A}\models s\theta \ge t\theta \). There are the following subcases.
-
(a)
\(s = f(s_1,\dots ,s_n)\) and \(s_i \sqsupseteq _\mathsf {WPO}t\) for some \(i \in \pi (f)\): In this case, we know \(s_i\theta \sqsupseteq _\mathsf {WPO}t\theta \) by induction hypothesis on s. Thus (2a) concludes \(s\theta \sqsupseteq _\mathsf {WPO}t\theta \).
-
(b)
\(s = f(s_1,\dots ,s_n)\), \(t = g(t_1,\dots ,t_m)\), and \(s \sqsupset _\mathsf {WPO}t_j\) for every \(j \in \pi (g)\): By induction hypothesis on t, we have \(s\theta \sqsupset _\mathsf {WPO}t_j\theta \). So the precondition of (2b) for \(s\theta \sqsupseteq _\mathsf {WPO}t\theta \) is satisfied. There are the following subcases:
-
(c)
\(s = t \in \mathcal {V}\): Then we have \(s\theta \sqsupseteq _\mathsf {WPO}t\theta \) by Lemma 1. \(\square \)
-
(a)
Irreflexivity of \(\sqsupset _\mathsf {WPO}\) is less obvious to have. In fact, [36] uses well-foundedness to claim it. Here we identify more essential conditions.
Lemma 3
If \(\langle \ge ,>\rangle \) is an order pair on \(\mathcal {A}\), and \(\succ \) is irreflexive on \(\mathcal {F}\), and \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple, then \(\sqsupset _\mathsf {WPO}\) is irreflexive.
Proof
We show \(s \not \sqsupset _\mathsf {WPO}s\) for every s by induction on the structure of s. This is clear if \(s \in \mathcal {V}\), so consider \(s = f(s_1,\dots ,s_n)\). Since > is irreflexive, we have  , and thus \(s \sqsupset _\mathsf {WPO}s\) cannot be due to case 1 of Definition 5. As \(\succ \) is irreflexive on \(\mathcal {F}\), \(f \nsucc f\) and thus (2b-i) is not possible, either. Thanks to induction hypothesis and the fact that lexicographic extension preserves irreflexivity, we have
, and thus \(s \sqsupset _\mathsf {WPO}s\) cannot be due to case 1 of Definition 5. As \(\succ \) is irreflexive on \(\mathcal {F}\), \(f \nsucc f\) and thus (2b-i) is not possible, either. Thanks to induction hypothesis and the fact that lexicographic extension preserves irreflexivity, we have  , and thus (2b-ii) is not possible either.
, and thus (2b-ii) is not possible either.
The remaining (2a) is more involving. To show \(s_i \not \sqsupseteq _\mathsf {WPO}f(s_1,\dots ,s_n)\) for any \(i \in \pi (f)\), we prove the following more general claim: \(s' \vartriangleleft _\pi ^+ s\) implies \(s' \not \sqsupseteq _\mathsf {WPO}s\), where \(\vartriangleleft _\pi \) denotes the least relation such that \(s_i \vartriangleleft _\pi f(s_1,\dots ,s_n)\) if \(i \in \pi (f)\). This claim is proved by induction on \(s'\). Due to the simplicity assumption, we have \(\mathcal {A}\models s \ge s'\) for every \(s' \vartriangleleft _\pi s\), and this generalizes for every \(s' \vartriangleleft _\pi ^+ s\) by easy induction and the transitivity of \(\ge \). Thus we cannot have \(\mathcal {A}\models s' > s\), since \(\mathcal {A}\models s \ge s' > s\) contradicts the assumption that \(\langle \ge ,>\rangle \) is an order pair. This tells us that \(s' \sqsupseteq _\mathsf {WPO}s\) cannot be due to case 1. Case (2a) is not applicable thanks to (inner) induction hypothesis on \(s'\). Case (2b) is not possible either, since \(s' \not \sqsupset _\mathsf {WPO}s'\) thanks to (outer) induction hypothesis on s. This concludes \(s' \not \sqsupseteq _\mathsf {WPO}s\) for any \(s' \vartriangleleft _\pi ^+ s\), and in particular \(s_i \not \sqsupseteq _\mathsf {WPO}s\) for any \(i \in \pi (f)\), refuting the last possibility for \(s \sqsupset _\mathsf {WPO}s\) to hold. \(\square \)
5 Co-WPO
The preceding section demonstrated how to use \(\mathsf {WPO}\) as a rewrite pair in Theorem 1. In this section we show how to use \(\mathsf {WPO}\) in combination with Theorem 2, that is, when \({\sqsupseteq } = {\sqsupseteq _\mathsf {WPO}}\), what \(\sqsubset \) should be. We show that \(\sqsubset _{\overline{\mathsf {WPO}}}\), where \({\overline{\mathsf {WPO}}}\mathrel {\,:=\,}\mathsf {WPO}(\pi ,\mathcal {A},{\nless },{\nleq },{\nprec },{\not \precsim })\), serves the purpose.
Proposition 2
If \(\langle \ge ,>\rangle \) and \(\langle \succeq ,\succ \rangle \) are order pairs on \(\mathcal {A}\) and \(\mathcal {F}\), \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple and monotone, then \(\langle \sqsupseteq _\mathsf {WPO},\sqsubset _{\overline{\mathsf {WPO}}}\rangle \) is a co-rewrite pair.
When \(\langle \mathcal {A},\ge \rangle \) is not total, Example 3 also demonstrates that using Proposition 2 with Theorem 2 is more powerful than using Proposition 1 in combination with Theorem 1, by taking \(\pi (f) = [\,]\) for every f. At the time of writing, however, it is unclear to the author if the difference still exists when \(\langle \mathcal {A},\ge \rangle \) is totally ordered but \(\langle \mathcal {F},\succeq \rangle \) is not. Nevertheless we will clearly see the merit of Proposition 2 under the setting of conditional rewriting in the next section.
The remainder of this section proves Proposition 2. Unfortunately, \({\overline{\mathsf {WPO}}}\) does not satisfy many important properties of \(\mathsf {WPO}\), mostly due to the fact that \(\langle \nless ,\nleq \rangle \) is not even an order pair. Nevertheless, Lemma 2 is applicable to \(\sqsupset _{\overline{\mathsf {WPO}}}\) and gives the following fact:
Lemma 4
If \(\langle \ge ,>\rangle \) is an order pair on \(\mathcal {A}\), \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple, and \(\succ \) is irreflexive, then \(\sqsupset _{\overline{\mathsf {WPO}}}\) is closed under substitutions.
Proof
We apply Lemma 2 to \({\overline{\mathsf {WPO}}}\). To this end, we need to prove the following:
-
\(\langle \mathcal {A},\nless \rangle \) is \(\pi \)-simple: Suppose on the contrary one had \([f]_{}(a_1,\dots ,a_n) < a_i\) with \(i \in \pi (f)\). Due to the simplicity assumption, we have \([f]_{}(a_1,\dots ,a_n) \ge a_i\). By compatibility we must have \(a_i < a_i\), contradicting irreflexivity.
-
\(\nless \) and \(\nprec \) are reflexive: This follows from the irreflexivity of < and \(\prec \). \(\square \)
The remaining task is to show that \({\sqsupseteq _\mathsf {WPO}} \cap {\sqsubset _{\overline{\mathsf {WPO}}}} = \emptyset \). Due to the mutual inductive definition of WPO, we need to simultaneously prove the property for the other combination: \({\sqsupseteq _{\overline{\mathsf {WPO}}}} \cap {\sqsubset _\mathsf {WPO}} = \emptyset \).
Definition 7
We say that two pairs \(P = \langle \sqsupseteq _P,\sqsupset _P\rangle \) and \(Q = \langle \sqsupseteq _Q,\sqsupset _Q\rangle \) of relations are co-compatible iff \({\sqsupseteq _P} \cap {\sqsubset _Q} = {\sqsupset _P} \cap {\sqsubseteq _Q} = \emptyset \).
The next claim is a justification for the word “compatible” in Definition 7. Here the compatibility assumption of order pairs is crucial.
Proposition 3
An order pair \(\langle \sqsupseteq ,\sqsupset \rangle \) is co-compatible with itself.
Proof
Suppose on the contrary that \(a \sqsupseteq b\) and \(b \sqsupset a\). Then we have \(a \sqsupset a\) by compatibility, contradicting the irreflexivity of \(\sqsupset \). \(\square \)
Lemma 5
If \(P = \langle \sqsupseteq _P,\sqsupset _P\rangle \) and \(Q = \langle \sqsupseteq _Q,\sqsupset _Q\rangle \) are co-compatible pairs of relations, then \(\langle \sqsupseteq _P^\mathsf {lex},\sqsupset _P^\mathsf {lex}\rangle \) and \(\langle \sqsupseteq _Q^\mathsf {lex}, \sqsupset _Q^\mathsf {lex}\rangle \) are co-compatible.
Proof
Let us assume that both
hold and derive a contradiction. The other part \({\sqsupset _P^\mathsf {lex}} \cap {\sqsubseteq _Q^\mathsf {lex}}\) is analogous. We proceed by induction on the length of \([s_1,\dots ,s_n]\). If \(n=0\), then (2) demands \(m=0\) but (3) demands \(m>0\). Hence we have \(n > 0\), and then (3) demands \(m>0\). If  then by assumption we have
then by assumption we have  but (3) demands
but (3) demands  (or
(or  ). Hence (2) is due to
). Hence (2) is due to  and \([s_2,\dots ,s_n] \sqsupseteq _P^\mathsf {lex}[t_2,\dots ,t_m]\). By assumption we have
and \([s_2,\dots ,s_n] \sqsupseteq _P^\mathsf {lex}[t_2,\dots ,t_m]\). By assumption we have  , so (3) is due to
, so (3) is due to  and \([s_2,\dots ,s_n] \sqsubset _Q^\mathsf {lex}[t_2,\dots ,t_m]\). We derive a contradiction by induction hypothesis.
and \([s_2,\dots ,s_n] \sqsubset _Q^\mathsf {lex}[t_2,\dots ,t_m]\). We derive a contradiction by induction hypothesis.
\(\square \)
We arrive at the main lemma for \({\overline{\mathsf {WPO}}}\).
Lemma 6
If \(\langle \ge ,>\rangle \) and \(\langle \succsim ,\succ \rangle \) are order pairs on \(\mathcal {A}\) and \(\mathcal {F}\), and \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple, then \(\mathsf {WPO}\) and \({\overline{\mathsf {WPO}}}\) are co-compatible.
Proof
We show that neither \(s \sqsupseteq _\mathsf {WPO}t \wedge s \sqsubset _{\overline{\mathsf {WPO}}}t\) nor \(s \sqsupset _\mathsf {WPO}t \wedge s \sqsubseteq _{\overline{\mathsf {WPO}}}t\) hold for any s and t, by induction on the structure of s and then t. Let us assume \(s \sqsupseteq _\mathsf {WPO}t\) and prove  . The other claim is analogous. We proceed by case analysis on the derivation of \(s \sqsupseteq _\mathsf {WPO}t\).
. The other claim is analogous. We proceed by case analysis on the derivation of \(s \sqsupseteq _\mathsf {WPO}t\).
-
1.
\(\mathcal {A}\models s > t\): Then
 cannot hold as it demands \(\mathcal {A}\models s \ngtr t\) (or \(s \ngeq t\)).
cannot hold as it demands \(\mathcal {A}\models s \ngtr t\) (or \(s \ngeq t\)). -
2.
\(\mathcal {A}\models s \ge t\): Then \(\mathcal {A}\models s \ngeq t\) cannot happen and thus \(s \sqsubset _{\overline{\mathsf {WPO}}}t\) must be due to case 2 of Definition 5. There are the following subcases for \(s \sqsupseteq _\mathsf {WPO}t\):
-
(a)
\(s = f(s_1,\dots ,s_n)\), \(s_i \sqsupseteq _\mathsf {WPO}t\) for some \(i \in \pi (f)\): By induction hypothesis on s, we have
 , and thus \(s \sqsubset _{\overline{\mathsf {WPO}}}t\) can only be due to (2a). So \(t = g(t_1,\dots ,t_m)\) and \(s \sqsubseteq _{\overline{\mathsf {WPO}}}t_j\) for some \(j \in \pi (g)\). Then \(s \not \sqsupset _\mathsf {WPO}t_j\) by induction hypothesis on t. On the contrary we must have \(s \sqsupset _\mathsf {WPO}t_j\): By Lemma 1– we have \(s \sqsupset _\mathsf {WPO}s_i \sqsupseteq _\mathsf {WPO}t \sqsupset _\mathsf {WPO}t_j\) and hence \(s \sqsupset _\mathsf {WPO}t_j\) as \(\langle \sqsupseteq _\mathsf {WPO},\sqsupset _\mathsf {WPO}\rangle \) is an order pair.
, and thus \(s \sqsubset _{\overline{\mathsf {WPO}}}t\) can only be due to (2a). So \(t = g(t_1,\dots ,t_m)\) and \(s \sqsubseteq _{\overline{\mathsf {WPO}}}t_j\) for some \(j \in \pi (g)\). Then \(s \not \sqsupset _\mathsf {WPO}t_j\) by induction hypothesis on t. On the contrary we must have \(s \sqsupset _\mathsf {WPO}t_j\): By Lemma 1– we have \(s \sqsupset _\mathsf {WPO}s_i \sqsupseteq _\mathsf {WPO}t \sqsupset _\mathsf {WPO}t_j\) and hence \(s \sqsupset _\mathsf {WPO}t_j\) as \(\langle \sqsupseteq _\mathsf {WPO},\sqsupset _\mathsf {WPO}\rangle \) is an order pair. -
(b)
\(s = f(s_1,\dots ,s_n)\), \(t = g(t_1,\dots ,t_m)\), and \(s \sqsupset _\mathsf {WPO}t_j\) for every \(j \in \pi (g)\): By induction hypothesis on t, we have \(s \not \sqsubseteq _{\overline{\mathsf {WPO}}}t_j\) for any \(j \in \pi (g)\). Thus \(s \sqsubset _{\overline{\mathsf {WPO}}}t\) must be due to (2b). We proceed by further considering the following two possibilities.
-
i.
\(f \succ g\): As neither \(f \nsucc g\) nor \(f \not \succsim g\) hold, \(s \sqsubseteq _{\overline{\mathsf {WPO}}}t\) is not possible.
-
ii.
\(f \succsim g\) and
 : As \(f \not \succsim g\) does not hold, (2b-i) is not applicable to have \(s \sqsubset _{\overline{\mathsf {WPO}}}t\). By Lemma 5 and induction hypothesis, we have
: As \(f \not \succsim g\) does not hold, (2b-i) is not applicable to have \(s \sqsubset _{\overline{\mathsf {WPO}}}t\). By Lemma 5 and induction hypothesis, we have  and thus (2b-ii) is also not applicable, either.
and thus (2b-ii) is also not applicable, either.
-
i.
-
(c)
\(s = t \in \mathcal {V}\): Then clearly \(s \sqsubset _{\overline{\mathsf {WPO}}}t\) cannot hold. \(\square \)
-
(a)
6 Conditional Rewriting
Conditional term rewriting (cf. [27]) is an extension of term rewriting so that rewrite rules can be guarded by conditions. We are interested in the “oriented” variants, as they naturally correspond to functional programming concepts such as where clauses of Haskell or when clauses of OCaml.
A conditional rewrite rule \(l \rightarrow r \Leftarrow \phi \) consists of terms l and r, and a list \(\phi \) of pairs of terms. We may omit “\(\Leftarrow [\,]\)” and write \(s_1 \twoheadrightarrow t_1,\dots ,s_n \twoheadrightarrow t_n\) for \([\langle s_1,t_1\rangle ,\dots ,\langle s_n,t_n\rangle ]\). A conditional TRS (CTRS) \(\mathcal {R}\) is a set of conditional rewrite rules. A CTRS \(\mathcal {R}\) yields the rewrite preorder \(\rightarrow _\mathcal {R}^*\) by the following derivation rules [22]:

To approximate reachability with respect to CTRSs by means of (co-)rewrite pairs, one needs to be careful when dealing with conditions.
Example 6
Consider the following CTRS:

and a reachability atom  . One might expect that a rewrite preorder \(\sqsupseteq \) such that
. One might expect that a rewrite preorder \(\sqsupseteq \) such that

can over-approximate  , but this is unfortunately false. For instance, any LPO satisfies the above constraints:
, but this is unfortunately false. For instance, any LPO satisfies the above constraints:  as LPO is a simplification order, and the second constraints also vacuously holds as the condition
as LPO is a simplification order, and the second constraints also vacuously holds as the condition  is false. However, it is unsound to conclude that
is false. However, it is unsound to conclude that  is
is  -unsatisfiable even if
-unsatisfiable even if  : by setting
: by setting  one can have
one can have  and
and  , but
, but  .
.
A solution is to use co-rewrite pairs already for dealing with conditions.
Proposition 4
If \(\langle \sqsupseteq ,\sqsubset \rangle \) is a co-rewrite pair, \(\left( l\rightarrow r \Leftarrow \phi \right) \in \mathcal {R}\) implies \(l \sqsupseteq r\) or \(u \sqsubset v\) for some \(u \twoheadrightarrow v \in \phi \), and \(s \sqsubset t\), then \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable.
Proof
We show that \(s \rightarrow _\mathcal {R}^* t\) implies \(s \sqsupseteq t\). This is sufficient, since, then \(s\theta \rightarrow _\mathcal {R}^* t\theta \) implies \(s\theta \sqsupseteq t\theta \), while \(s \sqsubset t\) demands \(s\theta \sqsubset t\theta \), which is not possible since \({\sqsupseteq } \cap {\sqsubset } = \emptyset \). The claim is proved by induction on the derivation of \(s \rightarrow _\mathcal {R}^* t\).
-
Refl: Since \(\sqsupseteq \) is reflexive, we have \(s \sqsupseteq s\).
-
Trans: We have \(s \rightarrow _\mathcal {R}t\) and \(t \rightarrow _\mathcal {R}^* u\) as premises, and \(s \sqsupseteq t\) and \(t \sqsupseteq u\) by induction hypothesis. Since \(\sqsupseteq \) is transitive we conclude \(s \sqsupseteq u\).
-
Mono: We have \(s_i \rightarrow _\mathcal {R}s_i'\) as a premise and \(s_i \sqsupseteq s_i'\) by induction hypothesis. Since \(\sqsupseteq \) is closed under contexts, we get \(f(s_1,\dots ,s_i,\dots ,s_n) \sqsupseteq f(s_1,\dots ,s_i',\dots ,s_n)\).
-
Rule: We have \(\left( l\rightarrow r \Leftarrow s_1\twoheadrightarrow t_1,\dots ,s_n\twoheadrightarrow t_n\right) \in \mathcal {R}\), and for every \(i \in \{1,\dots ,n\}\) have \(s_i\theta \rightarrow _\mathcal {R}^* t_i\theta \) as a premise and
 by induction hypothesis. Since \({\sqsupseteq } \cap {\sqsubset } = \emptyset \), we get
by induction hypothesis. Since \({\sqsupseteq } \cap {\sqsubset } = \emptyset \), we get  . Since \(\sqsubset \) is closed under substitutions, we conclude
. Since \(\sqsubset \) is closed under substitutions, we conclude  for every \(i \in \{1,\dots ,n\}\). By assumption, this entails \(l \sqsupseteq r\), and since \(\sqsupseteq \) is closed under substitution, we conclude \(l\theta \sqsupseteq r\theta \). \(\square \)
for every \(i \in \{1,\dots ,n\}\). By assumption, this entails \(l \sqsupseteq r\), and since \(\sqsupseteq \) is closed under substitution, we conclude \(l\theta \sqsupseteq r\theta \). \(\square \)
Example 7
Consider the following singleton CTRS:

Proposition 4 combined with \(\mathsf {LPO}\) or \(\mathsf {WPO}\) induced by a partial precedence such that  and
and  proves that
proves that  is
is  -unsatisfiable: Clearly
-unsatisfiable: Clearly  and
and  by case (2b-i) of Definition 5. On the other hand, Proposition 4 with the term ordering induced by a totally ordered algebra \(\langle \mathcal {A},\ge \rangle \) cannot solve the problem, since
by case (2b-i) of Definition 5. On the other hand, Proposition 4 with the term ordering induced by a totally ordered algebra \(\langle \mathcal {A},\ge \rangle \) cannot solve the problem, since  implies
implies  by totality, which then demands
by totality, which then demands  to satisfy the assumption of Proposition 4. For the same reason, \(\mathsf {WPO}\) induced by a totally ordered algebra and a total precedence cannot handle the problem either.
to satisfy the assumption of Proposition 4. For the same reason, \(\mathsf {WPO}\) induced by a totally ordered algebra and a total precedence cannot handle the problem either.
Note that the condition of the rule in  is unsatisfiable, and this is one of the two cases where Proposition 4 is effective. The other case is when a condition can be ignored. Proposition 4 is incomplete when conditions are essential, as in Example 6. For dealing with essential conditional rules, the variable binding in a rule should be taken into account. At this point, a model-oriented formulation (a la [19]) seems more suitable.
is unsatisfiable, and this is one of the two cases where Proposition 4 is effective. The other case is when a condition can be ignored. Proposition 4 is incomplete when conditions are essential, as in Example 6. For dealing with essential conditional rules, the variable binding in a rule should be taken into account. At this point, a model-oriented formulation (a la [19]) seems more suitable.
Definition 8
(model of CTRS). We extend the notation \([s \sqsupset t]_{}\alpha \) of Definition 2 to \([\phi ]_{}\alpha \) for an arbitrary Boolean formula \(\phi \) with the single binary predicate \(\sqsupset \) in the obvious manner. We say \(\mathcal {A}= \langle A,[\cdot ]_{}\rangle \) validates \(\phi \), written \(\mathcal {A}\models \phi \), iff \([\phi ]_{}\alpha \) for every \(\alpha : \mathcal {V}\rightarrow A\). We say a related \(\mathcal {F}\)-algebra \(\langle \mathcal {A},\sqsupset \rangle \) is a model of a CTRS \(\mathcal {R}\) iffFootnote 3 \(\mathcal {A}\models l \sqsupset r \vee s_1\not \sqsupset t_1 \vee \dots \vee s_n\not \sqsupset t_n\) for every \((l\rightarrow r\Leftarrow s_1\twoheadrightarrow t_1, \dots , s_n\twoheadrightarrow t_n) \in \mathcal {R}\).
Besides minor simplifications (e.g., we do not need two predicates as we are only concerned with reachability in many steps in this paper), the major difference with [19] is that here we do not encode the monotonicity or order axioms into logical formulas (using \(\overline{\mathcal {R}}\) of [19]). Instead, we impose these properties as meta-level assumptions over models.
Theorem 3
For a CTRS \(\mathcal {R}\), \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable if and only if there exists a monotone preordered model \(\langle \mathcal {A},\ge \rangle \) of \(\mathcal {R}\) such that \(\mathcal {A}\models s \ngeq t\).
Proof
We start with the “if” direction. Let \(\langle \mathcal {A},\ge \rangle \) be a monotone preordered model of \(\mathcal {R}\). As in Proposition 4, it suffices to show that \(s \rightarrow _\mathcal {R}^* t\) implies \(\mathcal {A}\models s \ge t\). The claim is proved by induction on the derivation of \(s \rightarrow _\mathcal {R}^* t\).
-
Refl: Since \(\ge \) is reflexive, we have \(\mathcal {A}\models s \ge s\).
-
Trans: We have \(s \rightarrow _\mathcal {R}t\) and \(t \rightarrow _\mathcal {R}^* u\) as premises, and \(\mathcal {A}\models s \ge t\) and \(\mathcal {A}\models t \ge u\) by induction hypothesis. Since \(\ge \) is transitive we conclude \(\mathcal {A}\models s \ge u\).
-
Mono: We have \(s_i \rightarrow _\mathcal {R}s_i'\) as a premise and \(\mathcal {A}\models s_i \ge s_i'\) by induction hypothesis. Since \(\langle \mathcal {A},\ge \rangle \) is monotone, we get \(\mathcal {A}\models f(s_1,\dots ,s_i,\dots ,s_n) \ge f(s_1,\dots ,s_i',\dots ,s_n)\).
-
Rule: We have \(\left( l\rightarrow r \Leftarrow s_1\twoheadrightarrow t_1,\dots ,s_n\twoheadrightarrow t_n\right) \in \mathcal {R}\), and for every \(i \in \{1,\dots ,n\}\) have \(s_i\theta \rightarrow _\mathcal {R}^* t_i\theta \) as a premise and \(\mathcal {A}\models s_i\theta \ge t_i\theta \) by induction hypothesis. Since \(\langle \mathcal {A},\ge \rangle \) is a model of \(\mathcal {R}\), and by the fact that validity is closed under substitutions, we have \(\mathcal {A}\models l\theta \ge r\theta \vee s_1\theta \ngeq t_1\theta \vee \dots \vee s_n\theta \ngeq t_n\theta \). Together with the induction hypotheses we conclude \(\mathcal {A}\models l\theta \ge r\theta \).
Next consider the “only if” direction. We show that \(\langle \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) ,\rightarrow _\mathcal {R}^*\rangle \) is a model of \(\mathcal {R}\), that is, for every \((l\rightarrow r\Leftarrow s_1\twoheadrightarrow t_1,\dots ,s_n\twoheadrightarrow t_n) \in \mathcal {R}\), we show \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \models l \rightarrow _\mathcal {R}^* r \vee s_1 \not \rightarrow _\mathcal {R}^* t_1 \vee \dots \vee s_n \not \rightarrow _\mathcal {R}^* t_n\). This means \(l\theta \rightarrow _\mathcal {R}^* r \theta \) for every \(\theta : \mathcal {V}\rightarrow \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \) such that \(s_1\theta \rightarrow _\mathcal {R}^* t_1\theta , \dots , s_n\theta \rightarrow _\mathcal {R}^* t_n\theta \), which is immediate by Rule. The fact that \(\rightarrow _\mathcal {R}^*\) is a preorder and closed under contexts is also immediate. Finally, \(s \twoheadrightarrow t\) being \(\mathcal {R}\)-unsatisfiable means that \(s\theta \not \rightarrow _\mathcal {R}^* t\theta \) for any \(\theta : \mathcal {V}\rightarrow \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), that is, \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \models s\not \rightarrow _\mathcal {R}^* t\). \(\square \)
Putting implementation issues aside, it is trivial to use semantic (termination) methods in Theorem 3.
Example 8
Consider again the CTRS  of Example 6. The monotone ordered
of Example 6. The monotone ordered  -algebra \(\langle \mathbb {N},[\cdot ]_{},\ge \rangle \) defined by
-algebra \(\langle \mathbb {N},[\cdot ]_{},\ge \rangle \) defined by

is a model of  , since for arbitrary \(x,y \in \mathbb {N}\), we have
, since for arbitrary \(x,y \in \mathbb {N}\), we have

Then, with Theorem 3 we can show that  is
is  -unsatisfiable, as
-unsatisfiable, as  for every \(x \in \mathbb {N}\).
for every \(x \in \mathbb {N}\).
To use \({\mathsf {WPO}(\mathcal {A})}\) in combination with Theorem 3, we need to validate formulas with predicate \(\sqsupseteq _{\mathsf {WPO}(\mathcal {A})}\) in the term algebra \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \). We encode these formulas into formulas with predicates \(\ge \) and >, which are then interpreted in \(\mathcal {A}\).
Definition 9
(formal WPO). Let \(\langle \ge ,>\rangle \) and \(\langle \succsim ,\succ \rangle \) be pairs of relations over some set and over \(\mathcal {F}\), respectively, and let \(\pi \) be a partial status. We define \(\mathtt {wpo}(\pi ,\ge ,>,\succsim ,\succ )\) or \(\mathtt {wpo}\) for short to be the pair \(\langle \sqsupseteq _\mathtt {wpo},\sqsupset _\mathtt {wpo}\rangle \), where for terms \(s,t \in \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \), \(s \sqsupseteq _\mathtt {wpo}t\) and \(s \sqsupset _\mathtt {wpo}t\) are Boolean formulas defined as follows:

where \(\phi \) is \(\textsc {False}\) if \(s \in \mathcal {V}\) and is  if \(s = f(s_1,\dots ,s_n)\), and \(\psi \) is \(\textsc {False}\) if \(t \in \mathcal {V}\) and is
if \(s = f(s_1,\dots ,s_n)\), and \(\psi \) is \(\textsc {False}\) if \(t \in \mathcal {V}\) and is

if \(t = g(t_1,\dots ,t_m)\). Formula \(s \sqsupseteq _\mathtt {wpo}t\) is defined analogously, except that \(\phi \) is \(\textsc {True}\) if \(s=t\in \mathcal {V}\), and \(\sqsupset _\mathtt {wpo}^\mathsf {lex}\) in formula \(\psi \) is replaced by \(\sqsupseteq _\mathtt {wpo}^\mathsf {lex}\).
We omit an easy proof that verifies that \(\mathtt {wpo}\) encodes \(\mathsf {WPO}\):
Lemma 7
 .
.
Note carefully that \(s \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\) is  but not \(\mathcal {A}\models s \not \sqsupseteq _\mathtt {wpo}t\). Hence we ensure \(s \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\) by \(\mathcal {A}\models s\sqsubseteq _{\overline{\mathtt {wpo}}}t\), where \({\overline{\mathtt {wpo}}}\) denotes \(\mathtt {wpo}(\pi ,\nless ,\nleq ,\nprec ,\not \precsim )\).
but not \(\mathcal {A}\models s \not \sqsupseteq _\mathtt {wpo}t\). Hence we ensure \(s \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\) by \(\mathcal {A}\models s\sqsubseteq _{\overline{\mathtt {wpo}}}t\), where \({\overline{\mathtt {wpo}}}\) denotes \(\mathtt {wpo}(\pi ,\nless ,\nleq ,\nprec ,\not \precsim )\).
Theorem 4
If \(\mathcal {R}\) is a CTRS, \(\langle \ge ,>\rangle \) and \(\langle \succsim ,\succ \rangle \) are order pairs on \(\mathcal {A}\) and \(\mathcal {F}\), \(\langle \mathcal {A},\ge \rangle \) is \(\pi \)-simple and monotone, \(\mathcal {A}\models l \sqsupseteq _\mathtt {wpo}r \vee u_1 \sqsubset _{\overline{\mathtt {wpo}}}v_1 \vee \dots \vee u_n \sqsubset _{\overline{\mathtt {wpo}}}v_n\) for every \(\left( l \rightarrow r \Leftarrow u_1\twoheadrightarrow v_1,\dots ,u_n\twoheadrightarrow v_n\right) \in \mathcal {R}\), and \(\mathcal {A}\models s \sqsubset _{\overline{\mathtt {wpo}}}t\), then \(s \twoheadrightarrow t\) is \(\mathcal {R}\)-unsatisfiable.
Proof
We apply Theorem 3. To this end, we first show that \(\langle \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) ,\sqsupseteq _{\mathsf {WPO}(\mathcal {A})}\rangle \) is a monotone preordered model of \(\mathcal {R}\). Monotonicity and preorderedness are due to Proposition 1. For being a model, let \(\left( l \rightarrow r \Leftarrow u_1\twoheadrightarrow v_1,\dots ,u_n\twoheadrightarrow v_n\right) \in \mathcal {R}\). Due to assumption and Lemma 7, we have \(l \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}r \vee u_1 \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}v_1 \vee \dots \vee u_n \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}v_n\). Due to Lemmas 2 and 4, we get \(l\theta \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}r\theta \vee u_1\theta \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}v_1\theta \vee \dots \vee u_n\theta \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}v_n\theta \) for every \(\theta : \mathcal {V}\rightarrow \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \). With Proposition 2 we conclude \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \models l \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}r \vee u_1\not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}v_1 \vee \dots \vee u_n\not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}v_n\). Finally, we need \(\mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \models s \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\), i.e., \(s\theta \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\theta \) for any \(\theta : \mathcal {V}\rightarrow \mathcal {T}\!\left( \mathcal {F},\mathcal {V}\right) \). As we assume \(s \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}t\), by Lemma 4 we have \(s\theta \sqsubset _{{\overline{\mathsf {WPO}}}(\mathcal {A})}t\theta \). By Proposition 2 we conclude \(s\theta \not \sqsupseteq _{\mathsf {WPO}(\mathcal {A})}t\theta \). \(\square \)
7 Experiments
The proposed methods are implemented in the termination prover NaTT [35], available at https://www.trs.cm.is.nagoya-u.ac.jp/NaTT/.
Internally, NaTT reduces the problem of finding an algebra \(\mathcal {A}\) that make \(\langle \mathcal {A},\ge \rangle \) a model of a TRS \(\mathcal {R}\) (or \(\sqsupseteq _{\mathsf {WPO}(\mathcal {A})}\subseteq \mathcal {R}\)) into a satisfiability modulo theory (SMT) problem, which is then solved by the backend SMT solver z3 [26]. The implementation of Theorem 1 and Corollary 1 is a trivial adaptation from the termination methods. Cororllary 2 is also trivial for totally ordered carriers, since \(\mathcal {A}\models s \ngeq t\) is equivalent to \(\mathcal {A}\models s < t\). Matrix/tuple interpretations are also easy, since \(\mathcal {A}\models \left( a_1,\dots ,a_n\right) \ngeq \left( b_1,\dots ,b_n\right) \) is equivalent to \(\mathcal {A}\models a_1< b_1 \vee \dots \vee a_n < b_n\). Theorem 2 with \({\overline{\mathsf {WPO}}}\) is obtained by parametrizing \(\mathsf {WPO}\).
Theorem 3 needs some tricks. In the unconditional case, finding a desired algebra \(\mathcal {A}\) can be encoded into SMT over quantifier-free linear arithmetic for a large class of \(\mathcal {A}\) [36]. For the conditional case, we need to find (\(\exists \)) parameters that validates (\(\forall \)) a disjunctive clause. Farkas’ lemma would reduce such a problem into quantifier-free SMT, but then the resulting problem is nonlinear. Experimentally, we observe that our backend z3 performs better on quantified linear arithmetic than quantifier-free nonlinear arithmetic, and hence we choose to leave the \(\forall \) quantifiers.
We conducted experiments using the examples presented in the paper and the examples in the INF category of the standard benchmark set COPS. The execution environment is StarExec [31] with the same settings as CoCo 2019.
Many COPS examples contain conjunctive reachability constraints of form \(s_1 \twoheadrightarrow t_1 \wedge \dots \wedge s_n \twoheadrightarrow t_n\). In this experiment we naively collapsed such a constraint into  by introducing a fresh function symbol
by introducing a fresh function symbol  . Two benchmarks exceed the scope of oriented CTRSs, on which NaTT immediately gives up.
. Two benchmarks exceed the scope of oriented CTRSs, on which NaTT immediately gives up.
As co-rewrite pairs we tested algebras \(\mathcal {S}{} \textit{um}\), \(\mathcal {S}{} \textit{um}^{+}\), \(\mathcal {S}{} \textit{um}^{-}\), \(\mathcal {M}{} \textit{at}\), LPO, and WPO. The basic algebra \(\mathcal {S}{} \textit{um}= \langle \mathbb {Z},[\cdot ]_{}\rangle \) is given by \([f]_{}(x_1,\dots ,x_n) = c_0 + \sum _{i=1}^{n} c_i\cdot x_i\), where \(c_0 \in \mathbb {Z}\), \(c_1,\dots ,c_n \in \{0,1\}\). Similarly \(\mathcal {S}{} \textit{um}^{+}\) and \(\mathcal {S}{} \textit{um}^{-}\) are defined, where the ranges of \(c_0\), which also determine the carrier, are \(\mathbb {N}\) and \(\mathbb {Z}_{\le 0}\), respectively. The algebra \(\mathcal {M}{} \textit{at}\) represents the 2D matrix interpretations.
Table 1 presents the results. For TRSs, we can observe that our proposed methods advance the state of the art, in the sense that they prove new examples that no tool previously participated in CoCo could handle. As there are only 15 TRS examples in the INF category of COPS 2021, we could not derive interesting observations there. Taking CTRS examples into account, we see \(\mathcal {S}{} \textit{um}\) is not as good as \(\mathcal {S}{} \textit{um}^+\) or \(\mathcal {S}{} \textit{um}^-\), while the carrier is bigger (\(\mathbb {Z}\) versus \(\mathbb {N}\) or \(\mathbb {Z}_{\le 0}\)). This phenomenon is explained as follows: For the latter two one knows variables are bounded by 0 (from below or above), and hence one can have  or
or  by
by  . Neither is possible when the carrier is unbounded. This observation also suggests another choice of carriers that are bounded from below and above, which is left for future work.
. Neither is possible when the carrier is unbounded. This observation also suggests another choice of carriers that are bounded from below and above, which is left for future work.
From the figures in CTRS examples, \(\mathcal {S}{} \textit{um}^-\) performs the best among our methods. However, \(\mathcal {M}{} \textit{at}\) and \(\mathsf {WPO}(\mathcal {S}{} \textit{um}^+)\) solve more examples if TRS examples are counted. It does not seem appropriate yet to judge practical significance from these experiments.
Finally, we implemented as the default strategy of NaTT 2.2 the sequential application of \(\mathcal {S}{} \textit{um}^-\), \(\mathsf {LPO}\), \(\mathsf {WPO}(\mathcal {S}{} \textit{um}^+)\), and \(\mathcal {M}{} \textit{at}\) after the test NaTT already have implemented. There improvement over previous NaTT 2.1 should be clear, although the number of timeouts (indicated by “TO:”) is significant.
8 Conclusion
We proposed generalizations of termination techniques that can prove unsatisfiability of reachability, both for term rewriting and for conditional term rewriting. We implemented the approach in the termination prover NaTT, and experimentally evaluated the significance of the proposed approach.
The implementation focused on evaluating the proposed methods separately. The only implemented way of combining their power is a naive one: apply the tests one by one while they fail. For future work, it will be interesting to incorporate the proposed method into the existing frameworks [10, 30].
Notes
- 1.
Such a property would be called inflationary in the mathematics literature. In the term rewriting, the word simple has been used (see, e.g., [32]) in accordance with simplification orders.
- 2.
When
 is the identity. KBO requires
is the identity. KBO requires  for any f.
for any f. - 3.
Here the formula \(s \not \sqsupset t\) is a shorthand for \(\lnot \ s \sqsupset t\).
References
Aoto, T.: Disproving confluence of term rewriting systems by interpretation and ordering. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 311–326. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_22
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Compt. Sci. 236(1–2), 133–178 (2000). https://doi.org/10.1016/S0304-3975(99)00207-8
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Dershowitz, N.: Orderings for term-rewriting systems. Theor. Compt. Sci. 17(3), 279–301 (1982). https://doi.org/10.1016/0304-3975(82)90026-3
Endrullis, J., Waldmann, J., Zantema, H.: Matrix interpretations for proving termination of term rewriting. J. Autom. Reason. 40(2–3), 195–220 (2008). https://doi.org/10.1007/s10817-007-9087-9
Feuillade, G., Genet, T., Tong, V.V.T.: Reachability analysis over term rewriting systems. J. Autom. Reasoning 33, 341–383 (2004). https://doi.org/10.1007/s10817-004-6246-0
Giesl, J., et al.: Proving termination of programs automatically with AProVE. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 184–191. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_13
Giesl, J., Rubio, A., Sternagel, C., Waldmann, J., Yamada, A.: The termination and complexity competition. In: Beyer, D., Huisman, M., Kordon, F., Steffen, B. (eds.) TACAS 2019. LNCS, vol. 11429, pp. 156–166. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17502-3_10
Giesl, J., Thiemann, R., Schneider-Kamp, P., Falke, S.: Mechanizing and improving dependency pairs. J. Autom. Reason. 37(3), 155–203 (2006). https://doi.org/10.1007/s10817-006-9057-7
Gutiérrez, R., Lucas, S.: Automatically proving and disproving feasibility conditions. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12167, pp. 416–435. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51054-1_27
Gutiérrez, R., Lucas, S.: mu-term: verify termination properties automatically (system description). In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12167, pp. 436–447. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51054-1_28
Hirokawa, N., Middeldorp, A.: Automating the dependency pair method. Inf. Comput. 199(1–2), 172–199 (2005). https://doi.org/10.1016/j.ic.2004.10.004
Kamin, S., Lévy, J.J.: Two generalizations of the recursive path ordering (1980). unpublished note
Knuth, D.E., Bendix, P.: Simple word problems in universal algebras. In: Computational Problems in Abstract Algebra, pp. 263–297. Pergamon Press, New York (1970). https://doi.org/10.1016/B978-0-08-012975-4.50028-X
Kop, C., Vale, D.: Tuple interpretations for higher-order complexity. In: Kobayashi, N. (ed.) FSCD 2021. LIPIcs, vol. 195, pp. 31:1–31:22. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.FSCD.2021.31
Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean termination tool 2. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 295–304. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02348-4_21
Kusakari, K., Nakamura, M., Toyama, Y.: Argument filtering transformation. In: Nadathur, G. (ed.) PPDP 1999. LNCS, vol. 1702, pp. 47–61. Springer, Heidelberg (1999). https://doi.org/10.1007/10704567_3
Lankford, D.: Canonical algebraic simplification in computational logic. Technical report ATP-25, University of Texas (1975)
Lucas, S., Gutiérrez, R.: Use of logical models for proving infeasibility in term rewriting. Inf. Process. Lett. 136, 90–95 (2018). https://doi.org/10.1016/j.ipl.2018.04.002
Lucas, S., Meseguer, J.: 2D dependency pairs for proving operational termination of CTRSs. In: Escobar, S. (ed.) WRLA 2014. LNCS, vol. 8663, pp. 195–212. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12904-4_11
Lucas, S., Meseguer, J.: Dependency pairs for proving termination properties of conditional term rewriting systems. J. Log. Algebraic Methods Program. 86(1), 236–268 (2017). https://doi.org/10.1016/j.jlamp.2016.03.003
Lucas, S., Meseguer, J., Gutiérrez, R.: The 2D dependency pair framework for conditional rewrite systems. part I: definition and basic processors. J. Comput. Syst. Sci. 96, 74–106 (2018). https://doi.org/10.1016/j.jcss.2018.04.002
Manna, Z., Ness, S.: Termination of Markov algorithms (1969). unpublished manuscript
Middeldorp, A.: Approximating dependency graphs using tree automata techniques. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 593–610. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_49
Middeldorp, A., Nagele, J., Shintani, K.: CoCo 2019: report on the eighth confluence competition. Int. J. Softw. Tools Technol. Transfer 23(6), 905–916 (2021). https://doi.org/10.1007/s10009-021-00620-4
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Ohlebusch, E.: Advanced Topics in Term Rewriting. Springer, New York (2002). https://doi.org/10.1007/978-1-4757-3661-8
Oostrom, V.: Sub-Birkhoff. In: Kameyama, Y., Stuckey, P.J. (eds.) FLOPS 2004. LNCS, vol. 2998, pp. 180–195. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24754-8_14
Sternagel, C., Thiemann, R., Yamada, A.: A formalization of weighted path orders and recursive path orders. Arch. Formal Proofs (2021). https://isa-afp.org/entries/Weighted_Path_Order.html, Formal proof development
Sternagel, C., Yamada, A.: Reachability analysis for termination and confluence of rewriting. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 262–278. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_15
Stump, A., Sutcliffe, G., Tinelli, C.: StarExec: a cross-community infrastructure for logic solving. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 367–373. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_28
TeReSe: Term Rewriting Systems, Cambridge Tracts in Theoretical Computer Science, vol. 55. Cambridge University Press, Cambridge (2003)
Thiemann, R., Schöpf, J., Sternagel, C., Yamada, A.: Certifying the weighted path order (invited talk). In: Ariola, Z.M. (ed.) FSCD 2020. LIPIcs, vol. 167, pp. 4:1–4:20. Schloss Dagstuhl-Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2020). https://doi.org/10.4230/LIPIcs.FSCD.2020.4
Yamada, A.: Multi-dimensional interpretations for termination of term rewriting. In: Platzer, A., Sutcliffe, G. (eds.) CADE 2021. LNCS (LNAI), vol. 12699, pp. 273–290. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79876-5_16
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya termination tool. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 466–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Yamada, A., Kusakari, K., Sakabe, T.: A unified ordering for termination proving. Sci. Comput. Program. 111, 110–134 (2015). https://doi.org/10.1016/j.scico.2014.07.009
Zantema, H.: Termination of term rewriting by semantic labelling. Fundam. Informaticae 24(1/2), 89–105 (1995). https://doi.org/10.3233/FI-1995-24124
Zantema, H.: The termination hierarchy for term rewriting. Appl. Algebr. Eng. Comm. Compt. 12(1/2), 3–19 (2001). https://doi.org/10.1007/s002000100061
Acknowledgments
The author would like to thank Kiraku Shintani for the technical help with the COPS database system. I would also like to thank Nao Hirokawa, Salvador Lucas, Naoki Nishida, and Sarah Winkler for discussions, and the anonymous reviewers for their detailed comments that improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Yamada, A. (2022). Term Orderings for Non-reachability of (Conditional) Rewriting. In: Blanchette, J., Kovács, L., Pattinson, D. (eds) Automated Reasoning. IJCAR 2022. Lecture Notes in Computer Science(), vol 13385. Springer, Cham. https://doi.org/10.1007/978-3-031-10769-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-031-10769-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-10768-9
Online ISBN: 978-3-031-10769-6
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  ,
, 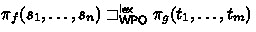 .
. , or
, or and
and  .
. : Then by induction hypothesis we have
: Then by induction hypothesis we have  , and thus
, and thus  cannot hold as it demands
cannot hold as it demands  , and thus
, and thus  : As
: As  and thus
and thus  by induction hypothesis. Since
by induction hypothesis. Since  . Since
. Since  for every
for every  is the identity. KBO requires
is the identity. KBO requires  for any f.
for any f.