Abstract
Faroldi argues that deontic modals are hyperintensional and thus traditional modal logic cannot provide an appropriate formalization of deontic situations. To overcome this issue, we introduce novel justification logics as hyperintensional analogues to non-normal modal logics. We establish soundness and completness with respect to various models and we study the problem of realization.
This work was supported by the Swiss National Science Foundation grant 200020_184625.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Artemov, S.: Explicit provability and constructive semantics. BSL 7(1), 1–36 (2001)
Artemov, S.: Justified common knowledge. TCS 357(1–3), 4–22 (2006)
Artemov, S.: The ontology of justifications in the logical setting. Stud. Log. 100(1–2), 17–30 (2012)
Artemov, S., Fitting, M.: Justification Logic: Reasoning with Reasons. Cambridge University Press, Cambridge (2019)
Bucheli, S., Kuznets, R., Studer, T.: Justifications for common knowledge. Appl. Non-Class. Log. 21(1), 35–60 (2011)
Faroldi, F.L., Ghari, M., Lehmann, E., Studer, T.: Impossible and conflicting obligations in justification logic. In: Marra, A., Liu, F., Portner, P., Van De Putte, F. (eds.) Proceedings of the DEON 2020 (2020)
Faroldi, F.L.G.: Deontic modals and hyperintensionality. Log. J. IGPL 27, 387–410 (2019)
Faroldi, F.L.G.: Normative properties and higher-order supervenience. In: Hyperintensionality and Normativity, pp. 181–199. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-03487-0_8
Faroldi, F.L.G., Protopopescu, T.: A hyperintensional logical framework for deontic reasons. Log. J. IGPL 27, 411–433 (2019)
Fitting, M.: The logic of proofs, semantically. APAL 132(1), 1–25 (2005)
Forrester, J.W.: Gentle murder, or the adverbial samaritan. J. Philos. 81(4), 193–197 (1984)
Indrzejczak, A.: Admissibility of cut in congruent modal logics. Log. Log. Philos. 20(3), 189–203 (2011)
Kokkinis, I., Maksimović, P., Ognjanović, Z., Studer, T.: First steps towards probabilistic justification logic. Log. J. IGPL 23(4), 662–687 (2015)
Kuznets, R., Studer, T.: Justifications, ontology, and conservativity. In: Bolander, T., Braüner, T., Ghilardi, S., Moss, L. (eds.) Advances in Modal Logic, vol. 9, pp. 437–458. College Publications (2012)
Kuznets, R., Studer, T.: Weak arithmetical interpretations for the logic of proofs. Log. J. IGPL 24(3), 424–440 (2016)
Kuznets, R., Studer, T.: Logics of Proofs and Justifications. College Publications, Norcross (2019)
Lavendhomme, R., Lucas, T.: Sequent calculi and decision procedures for weak modal systems. Stud. Log. 66(1), 121–145 (2000)
Lehmann, E., Studer, T.: Subset models for justification logic. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds.) WoLLIC 2019. LNCS, vol. 11541, pp. 433–449. Springer, Heidelberg (2019). https://doi.org/10.1007/978-3-662-59533-6_26
Pacuit, E.: A note on some explicit modal logics. In: Proceedings of the 5th Panhellenic Logic Symposium, pp. 117–125. University of Athens, Athens, Greece, 25–28 July 2005
Pacuit, E.: Neighborhood Semantics for Modal Logic. Springer, Heidelberg (2017)
Renne, B.: Dynamic Epistemic Logic with Justification. PhD thesis, City University of New York, May 2008
Ross, A.: Imperatives and logic. Theoria 7 (1941)
Studer, T.: Decidability for some justification logics with negative introspection. JSL 78(2), 388–402 (2013)
Studer, T.: A conflict tolerant logic of explicit evidence. Log. Investig. 27(1), 124–144 (2021)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Soundness and Completeness with Respect to Basic Models
Theorem 8 (Soundness w.r.t. basic models)
The Logic \(\mathsf {JE}_{\mathsf {CS}}\) is sound with respect to basic models. For an arbitrary constant specifications \(\mathsf {CS}\) and any formula F,
Proof
As usual, the proof is by induction on the length of \(\mathsf {JE}_{\mathsf {CS}}\) derivations and a case distinction on the last rule. The only interesting case is when F is an instance of je. Suppose
Thus we have
By Definition 3 we find \(B \in \bigodot ^{\varepsilon (\lambda _1)} _{\varepsilon (\lambda _2)} \varepsilon (t)\). Hence, by the definition of basic model we get \(B \in \varepsilon (\mathsf {e}(\lambda _1, \lambda _2 , t))\), which is \(\varepsilon \Vdash [\mathsf {e}(\lambda _1, \lambda _2 , t)]B\).
To prove the completeness theorem, we need to know that \(\mathsf {JE}_{\mathsf {CS}}\) is consistent.
Lemma 4
For any constant specification \(\mathsf {CS}\), \(\mathsf {JE}_{\mathsf {CS}}\) is consistent.
Proof
As usual, one can show that \(\mathsf {JE}_{\mathsf {CS}}\) is a conservative extension of classical propositional logic. This immediately yields consistency of \(\mathsf {JE}_{\mathsf {CS}}\).
Definition 17
A set of formulas \(\varGamma \) is called \(\mathsf {JE}_{\mathsf {CS}}\)-consistent if for each finite subset \(\varSigma \subseteq \varGamma \), we have \(\nvdash _{\mathsf {CS}} \bigwedge \varSigma \rightarrow \bot \). The set \(\varGamma \) is maximal \(\mathsf {JE}_{\mathsf {CS}}\)-consistent if \(\varGamma \) is consistent and none of its proper supersets is.
As usual, any consistent set can be extended to a maximal consistent set.
Lemma 5 (Lindenbaum)
For each \(\mathsf {JE}_{\mathsf {CS}}\)-consistent set \(\varDelta \), there exists a maximal \(\mathsf {JE}_{\mathsf {CS}}\)-consistent set \(\varGamma \supseteq \varDelta \).
Lemma 6
For any constant specification \(\mathsf {CS}\) and any maximal \(\mathsf {JE}_{\mathsf {CS}}\)-consistent set \(\varGamma \), there is a canoncial basic model \(\varepsilon ^c\) induced by \(\varGamma \) that is defined as follows:
-
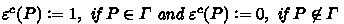 ;
; -
 ;
; -
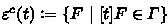 .
.
Proof
First we have to establish that \(\varepsilon ^c\) is a basic evaluation. We only show the condition
Suppose \(B \in \bigodot ^{\varepsilon ^c (\lambda _1)} _ {\varepsilon ^c (\lambda _2)} \varepsilon ^c (t)\), which means there is a formula \(A\in \varepsilon ^c (t)\) with \((A \rightarrow B) \in \varepsilon ^c (\lambda _1)\) and \((B \rightarrow A ) \in \varepsilon ^c (\lambda _2)\). By the definition of \(\varepsilon ^c\), we have
Since \(\varGamma \) is a maximal consistent set and
is an instance of je, we obtain \([\mathsf {e}(\lambda _1 , \lambda _2 , t)]B \in \varGamma \). This yields \(B \in \varepsilon ^c (e(\lambda _1, \lambda _2, t))\) and (12) is established.
Next, a truth lemma can be established as usual by induction on formula complexity. For all formulas F,
Finally, we show that our basic evaluation \(\varepsilon ^c\) is factive and hence a basic model. Suppose \(\varepsilon ^c \Vdash \lambda :F\). Hence \( \lambda :F \in \varGamma \). Since \(\varGamma \) is maximal consistent, we get by axiom jt that \(F \in \varGamma \). By (13) we conclude \(\varepsilon ^c \Vdash F\).
Using the Lindenbaum lemma, the canonical basic model and the established truth lemma (13), we immediately get the following completeness result.
Theorem 9 (Completeness w.r.t. basic models)
Let \(\mathsf {CS}\) be an arbitrary constant specification. The logic \(\mathsf {JE}_{\mathsf {CS}}\) is complete with respect to basic models. For any formula F,
B Soundness and Completeness with Respect to Modular Models
Theorem 10 (Soundness and completeness w.r.t. modular models)
Let \(\mathsf {CS}\) be an arbitrary constant specification. For each formula F we have
Proof
To prove soundness, suppose \(\mathcal {M}= \langle W, N, \varepsilon \rangle \) is a \(\mathsf {JE}_{\mathsf {CS}}\) modular model, and \(\mathsf {JE}_{\mathsf {CS}}\vdash A\). We need to show that A is true in every world \(w \in W\). Assume that \(\varepsilon _w\) is a basic model. Then by soundness with respect to basic models we get \(\varepsilon _w \Vdash A\) and by (11) we conclude \(\mathcal {M}, w \Vdash A\). It remains to show that \(\varepsilon _w\) indeed is a basic model, i.e. that it is factive. Suppose \(\varepsilon _w \Vdash \lambda : F\). By (11) we get \(\mathcal {M}, w \Vdash \lambda : F\). By factivitiy of modular models we get \(\mathcal {M}, w \Vdash F\) and by (11) again we conclude \(\varepsilon _w \Vdash F\).
For completeness, suppose that \(\mathsf {JE}_{\mathsf {CS}}\nvdash F\). Since \(\mathsf {JE}_{\mathsf {CS}}\) is complete with respect to basic models, there is a \(\mathsf {JE}_{\mathsf {CS}}\)-basic model \(\varepsilon \) with \(\varepsilon \nVdash F\). Now we construct a quasi-model  with
with  and
and
By (11) we find \(\mathcal {M}, w \nVdash F\). It only remains to show that \(\mathcal {M}\) is a modular model: Factivity follows immediately from (11) and the fact that \(\varepsilon \) is factive. To show (JYB), we suppose \(F \in \varepsilon ' _w(t)\). By the definition of N we get \(|F|^{\mathcal {M}} \in N(w)\), which means \(F \in \Box _w\).
C Soundness and Completeness with Respect to Fully Explanatory Modular Models
The next step is to prove that \(\mathsf {JE}_{\mathsf {CS}}\) is sound and complete with respect to fully explanatory \(\mathsf {JE}_{\mathsf {CS}}\) modular models. Before starting to prove the theorem, we need an auxiliary notion:
Definition 18 (Proof set)
Let \(\mathsf {M}_\mathsf {JE}\) be the set of all maximal \(\mathsf {JE}_{\mathsf {CS}}\)-consistent sets of formulas. We set
For any formula F we define \( \Vert F\Vert := \{ \varGamma \ | \ \varGamma \in \mathsf {M}_\mathsf {JE}\ \textit{and} \ F \in \varGamma \} \), called the proof set of F.
Proof sets share a number of properties, which are given in the following lemma.
Lemma 7
For formulas F, G following properties hold:
-
1.
\(\Vert F \wedge G\Vert = \Vert F\Vert \cap \Vert G\Vert \);
-
2.
\(\Vert \lnot F\Vert = \mathsf {M}_\mathsf {JE}\setminus \Vert F\Vert \);
-
3.
\(\Vert F \vee G\Vert = \Vert F\Vert \cup \Vert G\Vert \);
-
4.
\( \Vert F\Vert \subseteq \Vert G\Vert \ \text {iff} \ \vdash F \rightarrow G\);
-
5.
\(\vdash (F \leftrightarrow G) \ \text {iff} \ \Vert F\Vert =\Vert G\Vert \);
-
6.
if \(\Vert \lambda :G \Vert \subseteq \Vert G\Vert \) for any proof term \(\lambda \).
Proof
Let only show claim 4. The claim from right to left immediately follows from closure of maximal consistent sets under modus ponens. For the other direction, suppose \( \Vert F\Vert \subseteq \Vert G\Vert \), but not \(\vdash F \rightarrow G\). Then \(\lnot (F \rightarrow G)\) is consistent and by Lindenbaum’s Lemma there is a maximal consistent set \(\varGamma \ni \lnot (F \rightarrow G)\). This means \(F , \lnot G \in \varGamma \). Since \(F \in \varGamma \) and \( \Vert F\Vert \subseteq \Vert G\Vert \), we get \(G \in \varGamma \), which contradicts \(\lnot G \in \varGamma \).
Theorem 11 (Soundness and completeness for fully explanatory modular models)
Let \(\mathsf {CS}\) be an axiomatically appropriate constant specification. \(\mathsf {JE}_{\mathsf {CS}}\) is sound and complete with respect to fully explanatory \(\mathsf {JE}_{\mathsf {CS}}\) modular models.
Proof
Soundness is a direct conesquence of soundness for the class of \(\mathsf {JE}_{\mathsf {CS}}\) modular models.
To prove completeness, we define a canonical model  by
by
-
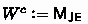 ;
; -
\(N^c : W^c \rightarrow \mathcal {P}(\mathcal {P}(W^c))\), such that for each maximal consistent set \(\varGamma \in W^c\),
$$ \Vert F\Vert \in N^c (\varGamma ) \ \text {iff} \ [t]F \in \varGamma , \ \text {for some} \ t \in \mathsf {JTm}\ ; $$ -
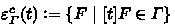 .
.
We define  . Now the canonical neighborhood function can be reformulated as
. Now the canonical neighborhood function can be reformulated as
Before establishing that this canonical model is a fully explanatory modular model, we show that the neighborhood function is well-defined. The issue is that different formulas may have the same proof set. Thus we need to show the following lemma.
Lemma 8
Let \(\mathsf {CS}\) be axiomatically appropriate. The neighborhood mapping \(N^c\) is well-defined, i.e. for any \(\varGamma \in \mathsf {M}_\mathsf {JE}\) and any formulas F, G, if \(\Vert F\Vert \in N(\varGamma ) \) and \(\Vert F\Vert = \Vert G\Vert \) then \([t]G \in \varGamma \) for some \(t \in \mathsf {JTm}\).
Proof
Let F, G be two formulas such that \(\Vert F\Vert = \Vert G\Vert \). For some \(\varGamma \in \mathsf {M}_\mathsf {JE}\), suppose \(\Vert F\Vert \in N^c( \varGamma )\). Thus \([s]F \in \varGamma \) for some \(s \in \mathsf {JTm}\) by the definition of the canonical model. By Lemma 7, we have \(\vdash F \leftrightarrow G\) and thus \(\vdash F \rightarrow G\) as well as \(\vdash G \rightarrow F\). Since \(\mathsf {CS}\) is axiomatically appropriate, there are proof terms \(\lambda _1 , \lambda _2\) such that \(\vdash \lambda _1 :(F \rightarrow G)\) and \(\vdash \lambda _2 :(G \rightarrow F)\). By the je axiom, we conclude \([\mathsf {e}(\lambda _1 , \lambda _2 , s)]G \in \varGamma \) .
Next we can establish the truth lemma.
Lemma 9 (Truth lemma)
For each formula F, we have \(|F|^{\mathcal {M}^c} = \Vert F\Vert \).
Proof
As usual the proof is by induction on the structure of F. We only show the case when F is [t]G. We have the following equivalences: \(\varGamma \in |[t]G|^{\mathcal {M}^c}\) iff \(\mathcal {M}^c , \varGamma \Vdash [t]G\) iff \(F \in \varepsilon ^c _\varGamma (t)\) iff \([t]F \in \varGamma \) iff \(\varGamma \in \Vert [t]F\Vert \).
Now we show that the canonical model is a modular model. First, we show that \(W^c \not = \emptyset \). Recall that by Lindenbaum’s Lemma, for every consistent set of formulas \(\varGamma \), there exist a maximally consistent set of formulas that contains \(\varGamma \). Since the empty set is consistent, by Lindenbaum’s Lemma, there is a maximal consistent set that contains the empty set and is an element of \(W^c\).
Next we show factivity. Suppose \(\mathcal {M}^c , \varGamma \Vdash \lambda :G\). By the truth lemma we get \(\lambda :G \in \varGamma \). Since \(\varGamma \) is maximally consistent, we obtain by axiom jt that \(G \in \varGamma \). Again by the truth lemma we conclude \(\mathcal {M}^c , \varGamma \Vdash G\).
Now we show that the canonicial model satisfies justificiation yields belief (JYB). Suppose \(F \in \varepsilon ^c _\varGamma (t)\) for some term t, some formula F, and some \(\varGamma \in W^c\). Since \(\varepsilon ^c _\varGamma (t)= \{ G \ | \ [t]G \in \varGamma \}\), we have \([t]F \in \varGamma \). By the definition of \(N^c\) we obtain \(\Vert F\Vert \in N^c (\varGamma )\). Thus, using the the truth lemma, we get \(|F|^{\mathcal {M}^c} \in N^c (\varGamma )\). Thus (JYB) is established.
It remains to show that the canoncial model is fully explanatory. Suppose \(|F|^{\mathcal {M}^c} \in N^c (\varGamma )\) for some formula F and some \(\varGamma \in W^c\). By the truth lemma we find \(\Vert F\Vert \in N^c (\varGamma )\). By the definition of \(N^c\), this implies \([t]F \in \varGamma \) for some term t. By the definition of \(\varepsilon ^c _\varGamma \) we finally conclude \(F \in \varepsilon ^c _\varGamma (t)\).
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Rohani, A., Studer, T. (2021). Explicit Non-normal Modal Logic. In: Silva, A., Wassermann, R., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2021. Lecture Notes in Computer Science(), vol 13038. Springer, Cham. https://doi.org/10.1007/978-3-030-88853-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-88853-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-88852-7
Online ISBN: 978-3-030-88853-4
eBook Packages: Computer ScienceComputer Science (R0)


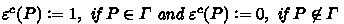 ;
; ;
;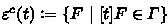 .
.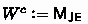 ;
;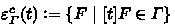 .
.