Abstract
This and the following two chapters discuss and criticize some existing systems of mathematics. This one is about classical mathematics as inspired by Georg Cantor, and especially its use of undefinable sets. The author refutes some arguments for actual infinity, and suggests that the picture the Cantorians provide of a realm of higher infinities is so unclear that there are good reasons to doubt they are even describing a possibility. More specifically, this chapter’s topics include the relationship between large cardinal axioms and theorems of arithmetic; Cantor’s two principles of generation for the transfinite ordinals; his proof that there are “more” real numbers than natural numbers; and the continuum hypothesis.
This chapter can be read in isolation from the rest of the book.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Following two different traditions, I am using the word “actually” in two different senses. Here, it is used in the Aristotelian sense, whereby actual infinity is opposed to potential infinity, while in the previous sentence, it was used in the modal sense, whereby actual existence is opposed to merely possible existence.
- 2.
For an overview, see Kanamori (2003).
- 3.
A similar point is made by Feferman (1987).
- 4.
One may cite another reason for believing in the consistency of ZFC: having an intuitive picture of the cumulative hierarchy. But because of my restrictive views about metaphysical possibility (see Chaps. 1 and 10), I would also only accept that as evidence for syntactical consistency, and not for (possible) truth.
- 5.
For definitions of ordinal addition, multiplication, and exponentiation see Cantor (1897, §14 and §18).
- 6.
“[W]enn irgendeine bestimmte Sukzession definierter ganzer realen Zahlen vorligt, von denen keine größte existiert, auf Grund dieses zweiten Erzeugungsprinzips eine neue Zahl geschaffen wird, welche als Grenze jener Zahlen gedacht, d.h. als die ihnen allen nächst größere Zahl definiert wird” (Cantor 1883, §11). (The emphasis here is taken from the quoted text. The same holds of emphasis in all other quotes in the present book, unless otherwise stated.)
- 7.
In contemporary set theory this route into the uncountable has been abandoned. Instead, the existence of ω1 is proved using (most notably) the powerset axiom and the axiom schema of replacement, as follows. The former implies the existence of
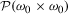 , which is the set of all binary relations on subsets of ω0. Any countable well-ordering is isomorphic to an ordering of a subset of ω0, and an ordering of a subset of ω0 is a binary relation on that subset of ω0. So the function that takes any well-ordering to its corresponding ordinal maps the subset of all well-orderings in
, which is the set of all binary relations on subsets of ω0. Any countable well-ordering is isomorphic to an ordering of a subset of ω0, and an ordering of a subset of ω0 is a binary relation on that subset of ω0. So the function that takes any well-ordering to its corresponding ordinal maps the subset of all well-orderings in 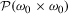 onto the set of all countable ordinals—its sethood is guaranteed by the axiom schema of replacement. Since an ordinal is the set of all its predecessors, this set is ω1. (This is a special case of the proof of Hartogs’s Theorem (Hartogs 1915).) The powerset axiom will be discussed in the next section.
onto the set of all countable ordinals—its sethood is guaranteed by the axiom schema of replacement. Since an ordinal is the set of all its predecessors, this set is ω1. (This is a special case of the proof of Hartogs’s Theorem (Hartogs 1915).) The powerset axiom will be discussed in the next section. - 8.
Loosely speaking, a well-ordering of an uncountable set can only be described if the set is well-ordered by design or defined from other sets that are. For instance, if we help ourselves to ω1, a well-ordering thereof can trivially be described using “∈”. However, such a trivial case does not help the plenitudinous combinatorialist here.
- 9.
This was first proved in Cantor (1874), but the version of the proof that has since become the best known is given in Cantor (1891).
- 10.
See Hodges (1998).
- 11.
The Löwenheim-Skolem Theorem states that a theory that is axiomatized in first-order logic with countably many axioms and that has an infinite model, has a model of any infinite cardinality (Löwenheim 1915; Skolem 1920). ZFC is an example of such a theory. Hence, the first-order powerset axiom,
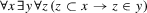 , can hold in a countable model, and thus does not capture what the plenitudinous combinatorialist aims at with the term “powerset”.
, can hold in a countable model, and thus does not capture what the plenitudinous combinatorialist aims at with the term “powerset”. - 12.
I do not dispute the (elementary) classical theorem according to which there is a bijection between the set of real numbers and the powerset of the set of natural numbers. Hence, just like in classical mathematics, we can use them interchangeably for purposes of discussions about size. I have used the former so far and will use the latter from here to the end of this chapter.
- 13.
In Cantor’s approach, ℵ0 is the result of abstracting from the order of the predecessors of ω0. In contemporary set theory, ℵ0 is simply the same object as ω0.
- 14.
In footnote 7, it was explained that the contemporary approach to establishing the existence of uncountable ordinals employs power sets. You might think that having one of the routes to higher infinity go via the other would help in comparing the two routes. But no, the problem remains.
- 15.
In fact, it cannot measure anything: among the uncountable sets that were first thought of by mathematicians independently of set theory, such as—in addition to the set of real numbers—the set of complex numbers, the set of functions from real numbers to real numbers, its subset of differentiable functions, etc., not a single one has had its size determined by one of Cantor’s alephs. The system of alephs is supposed to be a measuring system for infinite sizes, but except for the countable, it is a measuring system that can only measure itself. As such, it is a complete failure.
- 16.
There is not actually a unique intended model as the “the” indicates, because equally legitimate contestants can arguably differ with regard to the height of the hierarchy; but that is not relevant to a question about the second-smallest cardinal.
- 17.
In this paragraph I follow Chow (2009). It can be skipped by readers who do not care for these details.
- 18.
In more familiar terms: no suggestion for adding an axiom to ZFC that would settle the question and is intuitively true, assuming plenitudinous combinatorialism, has created anything approaching a consensus. For detailed discussion of the present situation, see Woodin (2001a, 2001b) and Koellner (2013).
- 19.
That there is a unique canonical version of the continuum hypothesis is argued in a similar way by Martin (2001).
References
Burali-Forti, C. (1897). Una questione sui numeri transfiniti. Rendiconti Del Circolo Matematico Di Palermo, 11, 154–164.
Cantor, G. (1874). Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen. Journal für die Reine und Angewandte Mathematik, 77, 258–262. Translated as “On a Property of the Set of Real Algebraic Numbers” in Ewald (1996).
Cantor, G. (1883). Grundlagen einer allgemeinen Mannigfaltigkeitslehre. Leipzig: Teubner. Translated as “Foundations of a general theory of manifolds” in Ewald (1996).
Cantor, G. (1891). Über eine elementare Frage der Mannigfaltigkeitslehre. Jaresbericht der Deutschen Mathematiker-Vereinigung, 1, 75–78. Translated as “On an Elementary Question in the Theory of Manifolds” in Ewald (1996).
Cantor, G. (1895/1897). Beiträge zur Begründung der transfiniten Mengenlehre. Mathematische Annalen, 46/49, 481–512/207–246. Translated as “Contributions to the Founding of the Theory of Transfinite Numbers” (1915). Dover Publications.
Chow, T. Y. (2009). A beginner’s guide to forcing. In Contemporary mathematics: Vol. 479. Communicating mathematics: a conference in honor of Joseph A. Gallian’s 65th birthday, July 16–19, 2007, University of Minnesota, Duluth, Minnesota. Providence: Am. Math. Soc.
Cohen, P. (1963). The independence of the continuum hypothesis. Proceedings of the National Academy of Sciences of the United States of America, 50, 1143–1148.
Cohen, P. (1964). The independence of the continuum hypothesis, II. Proceedings of the National Academy of Sciences of the United States of America, 51, 105–110.
Cohen, P. J. (1966). Set theory and the continuum hypothesis. New York: Benjamin.
Feferman, S. (1987). Infinity in mathematics: is Cantor necessary? In G. Toraldo di Francia (Ed.), L’infinito nella scienza, volume I (pp. 151–209). Instituto della Enciclopedia Italiana. Reprinted in Feferman (1998).
Gödel, K. (1940). The consistency of the continuum hypothesis. Princeton: Princeton University Press.
Hamkins, J. D. (2012). The set-theoretic multiverse. The Review of Symbolic Logic, 5, 416–449.
Hartogs, F. (1915). Über das Problem der Wohlordnung. Mathematische Annalen, 76, 438–443.
Hodges, W. (1998). An editor recalls some hopeless papers. The Bulletin of Symbolic Logic, 4, 1–16.
Kanamori, A. (2003). The higher infinite: large cardinals in set theory from their beginnings (2nd ed.). Berlin: Springer.
Koellner, P. (2013). The continuum hypothesis. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (Summer 2013 ed.).
Löwenheim, L. (1915). Über Möglichkeiten im Relativkalkül. Mathematische Annalen, 76, 447–470. Translated as “On possibilities in the calculus of relatives” in van Heijenoort (1967).
Martin, D. A. (2001). Multiple universes of sets and indeterminate truth values. Topoi, 20, 5–16.
Quine, W. (1969). Ontological relativity and other essays. New York: Columbia University Press.
Skolem, T. (1920). Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeit mathematischer Sätze nebst einem Theoreme über dichte Mengen. Videnskapsselskapet Skrifter, I. Matematisk-naturvidenskabelig Klasse, 4, 1–36.
Veblen, O. (1908). Continuous increasing functions of finite and transfinite ordinals. Transactions of the American Mathematical Society, 9, 280–292.
Woodin, W. H. (2001a). The continuum hypothesis, part I. Notices of the American Mathematical Society, 48, 567–576.
Woodin, W. H. (2001b). The continuum hypothesis, part II. Notices of the American Mathematical Society, 48, 681–690.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Hansen, C.S. (2021). Classical Mathematics and Plenitudinous Combinatorialism. In: Founding Mathematics on Semantic Conventions. Synthese Library, vol 446. Springer, Cham. https://doi.org/10.1007/978-3-030-88534-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-88534-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-88533-5
Online ISBN: 978-3-030-88534-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


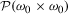 , which is the set of all binary relations on subsets of ω0. Any countable well-ordering is isomorphic to an ordering of a subset of ω0, and an ordering of a subset of ω0 is a binary relation on that subset of ω0. So the function that takes any well-ordering to its corresponding ordinal maps the subset of all well-orderings in
, which is the set of all binary relations on subsets of ω0. Any countable well-ordering is isomorphic to an ordering of a subset of ω0, and an ordering of a subset of ω0 is a binary relation on that subset of ω0. So the function that takes any well-ordering to its corresponding ordinal maps the subset of all well-orderings in 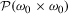 onto the set of all countable ordinals—its sethood is guaranteed by the axiom schema of replacement. Since an ordinal is the set of all its predecessors, this set is ω1. (This is a special case of the proof of Hartogs’s Theorem (
onto the set of all countable ordinals—its sethood is guaranteed by the axiom schema of replacement. Since an ordinal is the set of all its predecessors, this set is ω1. (This is a special case of the proof of Hartogs’s Theorem (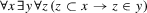 , can hold in a countable model, and thus does not capture what the plenitudinous combinatorialist aims at with the term “powerset”.
, can hold in a countable model, and thus does not capture what the plenitudinous combinatorialist aims at with the term “powerset”.