Abstract
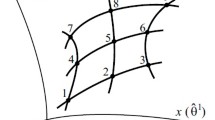
Using the Poisson equation and equations describing the plane stress state of plates as an example, the method of finite sums (two-dimensional integrating matrices) for the numerical solution of two-dimensional boundary value problems of the theory of elasticity is presented. According to this method, the original differential problem is preliminarily reduced to integral equations of the Volterra type, and then their approximation is carried out based on the replacement of the integrand by the Lagrange interpolation polynomial over Gaussian nodes. Two-dimensional integrating matrices are constructed. Numerical estimates of the accuracy of various test problems are carried out. It is shown that the convergence is exponential.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Birger, I.A.: Nekotoryye matematicheskiye metody resheniya inzhenernykh zadach [Some mathematical methods for solving engineering problems]. Oborongiz, Moscow (1956) [in Russian]
Vakhitov, M.B.: Integriruyushchiye matritsy – apparat chislennogo resheniya differentsial’nykh uravneniy stroitel’noy mekhaniki [Integrating matrices – apparatus for the numerical solution of differential equations of structural mechanics]. Russian Aeronautics. 3, 50–61 (1966) [in Russian]
Vakhitov, M.B., Safariyev, M.S., Snigirev, V.F.: Raschet kryl’yevykh ustroystv sudov na prochnost’ [Strength calculation of wing devices of ships]. Tat. kn. izd-vo, Kazan (1975) [in Russian]
Verlan’, A.F., Sizikov, V.S: Integral’nyye uravneniya: metody, algoritmy, programmy [Integral equations: methods, algorithms, programs]. Nauk. dumka, Kiyev (1986) [in Russian]
Ahlberg, J.H., Nilson, E.N., Walsh, J. L.: The theory of splines and their applications. Academic Press, New York (1967)
Vasilenko, V.A.: Splayn-funktsii: teoriya, algoritmy, programma [Spline functions: theory, algorithms, program]. Nauka. Sib. Otd-niye, Novosibirsk (1983) [in Russian]
Krylov, V.I., Bobkov, V.V., Monastyrskiy, P.I.: Vychislitel’nyye metody: V 2 t. [Computational methods: In 2 volumes]. Nauka, Moscow (1977) [in Russian]
Stechkin, S.B., Subbotin, YU.N.: Splayny v vychislitel’noy matematike [Splines in computational mathematics]. Nauka, Moscow (1976) [in Russian]
Paimushin, V.N., Firsov, V.A.: Obolochki iz Stekla. Raschet napryazhenno-deformirovannogo sostoyaniya [Glass shells. Calculation of the stress-strain state]. Mashinostroyeniye, Moscow (1993) [in Russian]
Dautov, R. Z., Paimushin, V. N.: On the method of integrating matrices for solving boundary value problems for ordinary equations of the fourth order. Russian Math. 40(10), 11–23 (1966)
Dautov, R. Z., Karchevsii, M.M., Paimushin, V. N.: On the method of integrating matrices for systems of ordinary differential equations. Russian Math. 47(7), 16–24 (2003)
Stepanova, Ye.M., Petrushenko Yu.Ya.: Algebraicheskiy analog zadachi Puassona na osnove integriruyushchikh matrits, baziruyushchikhsya na polinomakh [Algebraic analogue of the Poisson problem based on integrating matrices based on Lagrange polynomials]. Matematicheskoye modelirovaniye i krayevyye zadachi. Trudy Vserossiyskoy nauchnoy konferentsii. Samara. Samarskiy gosudarstvennyy tekhnicheskiy universitet. 212–214 (2004) [in Russian]
Stepanova, Ye.M., Dautov, R.Z., Petrushenko Yu.Ya.: Resheniye krayevykh zadach, opisyvayemykh dvumernymi ellipticheskimi uravneniyami vtorogo poryadka, metodom integriruyushchikh matrits [Solution of boundary value problems described by two-dimensional second-order elliptic equations by the method of integrating matrices]. Matematicheskoye modelirovaniye i krayevyye zadachi. Trudy Vtoroy Vserossiyskoy nauchnoy konferentsii. Samara. Samarskiy gosudarstvennyy tekhnicheskiy universitet. 218–221 (2005) [in Russian]
Acknowledgements
This paper has been supported by the Kazan Federal University Strategic Academic Leadership Program (“PRIORITY-2030”).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Paimushin, V.N., Makarov, M.V. (2022). Two-Dimensional Integrating Matrices for Solving Elasticity Problems in a Rectangular Domain by the Finite Sum Method. In: Badriev, I.B., Banderov, V., Lapin, S.A. (eds) Mesh Methods for Boundary-Value Problems and Applications. Lecture Notes in Computational Science and Engineering, vol 141. Springer, Cham. https://doi.org/10.1007/978-3-030-87809-2_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-87809-2_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-87808-5
Online ISBN: 978-3-030-87809-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)