Effect of Vorticity on Peregrine Breather for Interfacial Waves of Finite Amplitude

Abstract

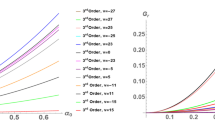
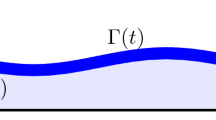
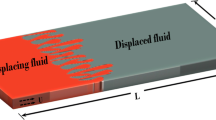
A third-order nonlinear Schrödinger equation (NLSE) in one space variable has been established for a finite amplitude wave propagating along the interface of the superposition of two finite depth fluids under the circumstance of a basic current shear. Starting from this two-dimensional (1+1) NLSE, we have discussed the stability analysis for a uniform wave train, considering both the cases of air–water interface and the Boussinesq approximation. Later, the effect of shear current on Peregrine breather for both types of aforesaid interfaces has been portrayed.

Appendix

The coefficients appearing in Eq. (21) are

$$\displaystyle \begin{aligned} \alpha&=\frac{1}{2}\left(\frac{dc_g}{dk} \right)_{k=1} =\frac{1}{f_\sigma}[(\sigma_1+r\sigma_2)c_g^2\\&\quad + \{ 2\sigma h_1(1-\sigma_1^2)+2\sigma rh_2(1-\sigma_2^2)-(\omega_2-r\omega_1)\delta_1 \}c_g & \\ &\quad -\sigma^2\{ \sigma_1h_1^2(1-\sigma_1^2)+r\sigma_2h_2^2(1-\sigma_2^2) \}\\&\quad - \{ (\omega_2-r\omega_1)\sigma+(1-r) \}(\delta_3-\delta_4) -(1-r)\delta_1 ], \end{aligned} $$

$$\displaystyle \begin{aligned}\mu&=\frac{1}{2\sigma_1^3\sigma_2^3f_\sigma}\left[ \frac{ 2\big\{ \sigma^2\sigma_1^2(1-\sigma_2^2)-r\sigma^2\sigma_2^2(1-\sigma_1^2)+ \frac{\sigma_2\sigma_1^2\delta_5(c_g-h_2\omega_2)}{h_2}-\frac{r\sigma_1\sigma_2^2\delta_6(c_g+h_1\omega_1)}{h_1} \big\}^2 }{ \frac{c_g^2}{h_2}+\frac{rc_g^2}{h_1}-\delta_7 } \right.\\ & \quad + \frac{ \{ \sigma^2\sigma_1^2(3-\sigma_2^2)-r\sigma^2\sigma_2^2(3-\sigma_1^2)-\omega_2\sigma_1^2\sigma_2(\delta_5+\sigma+\sigma\sigma_2^2)-r\omega_1(\delta_6+\sigma+\sigma\sigma_1^2) \}^2 }{\sigma^2\sigma_2+r\sigma^2\sigma_1} \\ &\quad -\frac{2\sigma_1^2\sigma_2^2(h_1\delta_5^2\sigma_1^2+rh_2\delta_6^2\sigma_2^2)}{h_1h_2}-\sigma_1\sigma_2\{ 4\sigma^2\sigma_1^3(1-2\sigma_2^2)+4r\sigma^2\sigma_2^3(1-2\sigma_1^2) \\ &\quad -\omega_2\sigma_2\sigma_1^3( 4\sigma(1-\sigma_2^2)-\omega_2\sigma_2(1+\sigma_2^2) ) \\&\quad +r\omega_1\sigma_1\sigma_2^3( 4\sigma(1-\sigma_1^2)+\omega_1\sigma_1(1+\sigma_1^2) ) \} ], & \end{aligned} $$

$$\displaystyle \begin{aligned} \delta_1&=\sigma_1 h_2(1-\sigma_2^2)+\sigma_2 h_1(1-\sigma_1^2), ~~~ \delta_2=\sigma_1+ h_1(1-\sigma_1^2),\\ \delta_3&=h_1h_2(1-\sigma_1^2)(1-\sigma_1^2), \end{aligned} $$

$$\displaystyle \begin{aligned} \delta_4&=\sigma_1\sigma_2\{ h_1^2(1-\sigma_1^2)+h_2^2(1-\sigma_2^2) \}, \delta_5=2\sigma-\sigma_2\omega_2,\delta_6=2\sigma+\sigma_1\omega_1, \\ \delta_7&=1-r+(\omega_2-r\omega_1)c_g. \end{aligned} $$