Abstract
Isabelle is a generic theorem prover with a fragment of higher-order logic as a metalogic for defining object logics. Isabelle also provides proof terms. We formalize this metalogic and the language of proof terms in Isabelle/HOL, define an executable (but inefficient) proof term checker and prove its correctness w.r.t. the metalogic. We integrate the proof checker with Isabelle and run it on a range of logics and theories to check the correctness of all the proofs in those theories.
Supported by Wirtschaftsministerium Bayern under DIK-2002-0027//DIK0185/03 and DFG GRK 2428 ConVeY
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
One of the selling points of proof assistants is their trustworthiness. Yet in practice soundness problems do come up in most proof assistants. Harrison [11] distinguishes errors in the logic and errors in the implementation (and cites examples). Our work contributes to the solution of both problems for the proof assistant Isabelle [31]. Isabelle is a generic theorem prover: it implements \(\mathcal {M}\), a fragment of intuitionistic higher-order logic, as a metalogic for defining object logics. Its most developed object logic is HOL and the resulting proof assistant is called Isabelle/HOL [24, 25]. The latter is the basis for our formalizations.
Our first contribution is the first complete formalization of Isabelle’s metalogic. Thus our work applies to all Isabelle object logics, e.g. not just HOL but also ZF. Of course Paulson [30] describes \(\mathcal {M}\) precisely, but only on paper. More importantly, his description does not cover polymorphism and type classes, which were introduced later [26]. The published account of Isabelle’s proof terms [4] is also silent about type classes. Yet type classes are a significant complication (as, for example, Kunčar and Popescu [18] found out).
Our second contribution is a verified (against \(\mathcal {M}\)) and executable checker for Isabelle’s proof terms. We have integrated the proof checker with Isabelle. Thus we can guarantee that every theorem whose proof our proof checker accepts is provable in our definition of \(\mathcal {M}\). So far we are able to check the correctness of moderatly sized theories across the full range of logics implemented in Isabelle.
Although Isabelle follows the LCF-architecture (theorems that can only be manufactured by inference rules) it is based on an infrastructure optimized for performance. In particular, this includes multithreading, which is used in the kernel and has once lead to a soundness issueFootnote 1 . Therefore we opt for the “certificate checking” approach (via proof terms) instead of verifying the implementation.
This is the first work that deals directly with what is implemented in Isabelle as opposed to a study of the metalogic that Isabelle is meant to implement. Instead of reading the implementation you can now read and build on the more abstract formalization in this paper. The correspondence of the two can be established for each proof by running the proof checker.
Our formalization reflects the ML implementation of Isabelle’s terms and types and some other data structures. Thus a few implementation choices are visible, e.g. De Bruijn indices. This is necessary because we want to integrate our proof checker as directly as possible with Isabelle, with as little unverified glue code as possible, for example no translation between De Bruijn indices and named variables. We refer to this as our intentional implementation bias. In principle, however, one could extend our formalization with different representations (e.g. named terms) and prove suitable isomorphisms. Our work is purely proof theoretic; semantics is out of scope.
The formalization can be found in the Archive of Formal Proofs[28].
2 Related Work
Harrison [11] was the first to verify some of HOL’s metatheory and an implementation of a HOL kernel in HOL itself. Kumar et al. [13] formalized HOL including definition principles, proved its soundness and synthesized a verified kernel of a HOL prover down to the machine language level. Abrahamsson [2] verified a proof checker for the OpenTheory [12] proof exchange format for HOL.
Wenzel [38] showed how to interpret type classes as predicates on types. We follow his approach of reflecting type classes in the logic but cannot remove them completely because of our intentional implementation bias (see above). Kunčar and Popescu [15,16,17,18] focus on the subtleties of definition principles for HOL with overloading and prove that under certain conditions, type and constant definitions preserve consistency. Åman Pohjola et al. [1] formalize [15, 18].
Adams [3] presents HOL Zero, a basic theorem prover for HOL that addresses the problem of how to ensure that parser and pretty-printer do not misrepresent formulas.
Let us now move away from Isabelle and HOL. Sozeau et al. [36] present the first implementation of a type checker for the kernel of Coq that is proved correct in Coq with respect to a formal specification. Carneiro [6] has implemented a highly performant proof checker for a multi-sorted first order logic and is in the process of verifying it in its own logic.
We formalize a logic with bound variables, and there is a large body of related work that deals with this issue (e.g. [7, 21, 37]) and a range of logics and systems with special support for handling bound variables (e.g. [33,34,35]). We found that De Bruijn indices worked reasonably well for us.
3 Preliminaries
Isabelle types are built from type variables, e.g.
 , and (postfix) type constructors, e.g.
, and (postfix) type constructors, e.g.
 ; the function type arrow is
; the function type arrow is
 . Isabelle also has a type class system explained later. The notation \(t \; {:}{:} \; \tau \) means that term t has type \(\tau \). Isabelle/HOL provides types
. Isabelle also has a type class system explained later. The notation \(t \; {:}{:} \; \tau \) means that term t has type \(\tau \). Isabelle/HOL provides types
 and
and
 of sets and lists of elements of type
of sets and lists of elements of type
 . They come with the following vocabulary: function
. They come with the following vocabulary: function
 (conversion from lists to sets),
(conversion from lists to sets),
 (list constructor),
(list constructor),
 (append),
(append),
 (length of list
(length of list
 ),
),
 (the
(the
 th element of
th element of
 starting at 0),
starting at 0),

 and other self-explanatory notation.
and other self-explanatory notation.
The
 of a relation
of a relation
 is the set of all
is the set of all
 such that
such that
 is in
is in
 .
.
There is also the predefined data type

The type
 abbreviates
abbreviates
 , i.e. partial functions, which we call maps. Maps have a domain and a range:
, i.e. partial functions, which we call maps. Maps have a domain and a range:

Logical equivalence is written
 instead of
instead of
 .
.
4 Types and Terms
A
 is simply a string. Variables have type
is simply a string. Variables have type
 ; their inner structure is immaterial for the presentation of the logic.
; their inner structure is immaterial for the presentation of the logic.
The logic has three layers: terms are classified by types as usual, but in addition types are classified by sorts. A
 is simply a set of class names. We discuss sorts in detail later.
is simply a set of class names. We discuss sorts in detail later.
Types (typically denoted by
 ,
,
 , ...) are defined like this:
, ...) are defined like this:

where

 represents the Isabelle type
represents the Isabelle type
 and
and
 represents a type variable
represents a type variable
 of sort
of sort
 — sorts are directly attached to type variables. The notation
— sorts are directly attached to type variables. The notation
 is short for
is short for
 is the name of the function type constructor.
is the name of the function type constructor.
Isabelle’s terms are simply typed lambda terms in De Bruijn notation:

A term (typically
 ,
,
 ,
,
 ,
,
 ...) can be a typed constant
...) can be a typed constant
 or free variable
or free variable
 , a bound variable
, a bound variable
 (a De Brujin index), a typed abstraction
(a De Brujin index), a typed abstraction
 or an application
or an application
 .
.
The term-has-type proposition has the syntax
 where
where
 is a list of types, the context for the type of the bound variables.
is a list of types, the context for the type of the bound variables.



We define
 .
.
Function
 collects the free variables in a term. Because bound variables are indices,
collects the free variables in a term. Because bound variables are indices,
 is simply the set of all
is simply the set of all
 occurs in
occurs in
 . The type is an integral part of a variable.
. The type is an integral part of a variable.
A type substitution is a function
 of type
of type
 . It assigns a type to each type variable and sort pair. We write
. It assigns a type to each type variable and sort pair. We write
 for the overloaded function which applies such a type substitution to all type variables (and their sort) occurring in a type or term. The type instance relation is defined like this:
for the overloaded function which applies such a type substitution to all type variables (and their sort) occurring in a type or term. The type instance relation is defined like this:

We also need to \(\beta \)-contract a term
 to something like “
to something like “
 with
with
 replaced by
replaced by
 ”. We define a function
”. We define a function
 such that
such that
 is that \(\beta \)-contractum. The definition of
is that \(\beta \)-contractum. The definition of
 is shown in the Appendix and can also be found in the literature (e.g. [23]).
is shown in the Appendix and can also be found in the literature (e.g. [23]).
In order to abstract over a free (term) variable there is a function
 that (roughly speaking) replaces all occurrences of
that (roughly speaking) replaces all occurrences of
 . Again, see the Appendix for the definition. This produces (if
. Again, see the Appendix for the definition. This produces (if
 occurs in
occurs in
 ) a term with an unbound
) a term with an unbound
 . Function
. Function
 binds it with an abstraction:
binds it with an abstraction:

While this section described the syntax of types and terms, they are not necessarily wellformed and should be considered pretypes/preterms. The wellformedness checks are described later.
5 Classes and Sorts
Isabelle has a built-in system of type classes [22] as in Haskell 98 except that class constraints are directly attached to variable names: our
 corresponds to Haskell’s (C a, D a, ...) => ... a ....
corresponds to Haskell’s (C a, D a, ...) => ... a ....
A
 is Isabelle’s terminology for a set of (class) names, e.g.
is Isabelle’s terminology for a set of (class) names, e.g.
 , which represent a conjunction of class constraints. In our work, variables
, which represent a conjunction of class constraints. In our work, variables
 etc. stand for sorts.
etc. stand for sorts.
Apart from the usual application in object logics, type classes also serve an important metalogical purpose: they allow us to restrict, for example, quantification in object logics to object-level types and rule out meta-level propositions.
Isabelle’s type class system was first presented in a programming language context [27, 29]. We give the first machine-checked formalization. The central data structure is a so-called order-sorted signature. Intuitively, it is comprised of a set of class names, a partial subclass ordering on them and a set of type constructor signatures. A type constructor signature
 for a type constructor
for a type constructor
 states that applying
states that applying
 to types
to types
 such that
such that
 has sort
has sort
 (defined below) produces a type of class
(defined below) produces a type of class
 . Formally:
. Formally:

To explain this formalization we start from a pair
 and recover the informal order-sorted signature described above. The set of classes is simply the
and recover the informal order-sorted signature described above. The set of classes is simply the
 of the
of the
 relation. The
relation. The
 component represents the set of all type constructor signatures
component represents the set of all type constructor signatures
 (where
(where
 is a list of sorts) such that
is a list of sorts) such that
 . Representing
. Representing
 as a triple, we define
as a triple, we define

 is the translation of
is the translation of
 , the data structure close to the implementation, to an equivalent but more intuitive version
, the data structure close to the implementation, to an equivalent but more intuitive version
 that is close to the informal presentations in the literature.
that is close to the informal presentations in the literature.
The subclass ordering
 can be extended to a subsort ordering as follows:
can be extended to a subsort ordering as follows:

The smaller sort needs to subsume all the classes in the larger sort. In particular
 iff
iff
 .
.
Now we can define a predicate
 that checks whether, in the context of some order-sorted signature
that checks whether, in the context of some order-sorted signature
 , a type fulfills a given sort constraint:
, a type fulfills a given sort constraint:

The rule for type variables uses the subsort relation and is obvious. A type
 has sort
has sort
 if for every
if for every
 there is a signature
there is a signature
 and
and
 for
for
 .
.
We normalize a sort by removing “superfluous” class constraints, i.e. retaining only those classes that are not subsumed by other classes. This gives us unique representatives for sorts which we call normalized:

We work with normalized sorts because it simplifies the derivation of efficient executable code later on.
Now we can define wellformedness of an
 :
:

A sublass relation is wellformed if it is a partial order where reflexivity is restricted to its
 . Wellformedness of type constructor signatures (
. Wellformedness of type constructor signatures (
 ) is more complex. We describe it in terms of
) is more complex. We describe it in terms of
 derived from
derived from
 (see above). The conditions are the following:
(see above). The conditions are the following:
-
The following property requires a) that for any
 there must be a
there must be a
 for every superclass
for every superclass
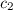 of
of
 and b) coregularity which guarantees the existence of principal types [10, 29].
and b) coregularity which guarantees the existence of principal types [10, 29].

-
A type constructor must always take the same number of argument types:

-
Sorts must be normalized and must exists in
 :
:
 where
where

These conditions are used in a number of places to show that the type system is well behaved. For example,
 is upward closed:
is upward closed:

6 Signatures
A signature consist of a map from constant names to their (most general) types, a map from type constructor names to their arities, and an order-sorted signature:

The three projection functions are called
 ,
,
 and
and
 . We now define a number of wellformedness checks w.r.t. a signature
. We now define a number of wellformedness checks w.r.t. a signature
 . We start with wellformedness of types, which is pretty obvious:
. We start with wellformedness of types, which is pretty obvious:


Wellformedness of a term essentially just says that all types in the term are wellformed and that the type
 of a constant in the term must be an instance of the type
of a constant in the term must be an instance of the type
 of that constant in the signature:
of that constant in the signature:
 .
.




These rules only check whether a term conforms to a signature, not that the contained types are consistent. Combining wellformedness and
 yields welltypedness of a term:
yields welltypedness of a term:

Wellformedness of a signature
 is defined as follows:
is defined as follows:

In words: all types in
 are wellformed,
are wellformed,
 is wellformed, the type constructors in
is wellformed, the type constructors in
 are exactly those that have an arity in
are exactly those that have an arity in
 , for every type constructor signature
, for every type constructor signature
 in
in
 ,
,
 .
.
7 Logic
Isabelle’s metalogic \(\mathcal {M}\) is an extension of the logic described by Paulson [30]. It is a fragment of intuitionistic higher-order logic. The basic types and connectives of \(\mathcal {M}\) are the following:

The type subscripts of
 and
and
 are dropped in the text if they can be inferred.
are dropped in the text if they can be inferred.
Readers familiar with Isabelle syntax must keep in mind that for readability we use the symbols
 ,
,
 and
and
 for the encodings of the respective symbols in Isabelle’s metalogic. We avoid the corresponding metalogical constants completely in favour of HOL’s
for the encodings of the respective symbols in Isabelle’s metalogic. We avoid the corresponding metalogical constants completely in favour of HOL’s
 ,
,
 ,
,
 and inference rule notation.
and inference rule notation.
The provability judgment of \(\mathcal {M}\) is of the form
 is a theory,
is a theory,
 (the hypotheses) is a set of terms of type
(the hypotheses) is a set of terms of type
 and
and
 a term of type
a term of type
 .
.
A theory is a pair of a signature and a set of axioms:

The projection functions are
 and
and
 . We extend the notion of wellformedness from signatures to theories:
. We extend the notion of wellformedness from signatures to theories:

The first two conjuncts need no explanation. Predicate
 (not shown) requires the signature to have certain minimal content: the basic types (
(not shown) requires the signature to have certain minimal content: the basic types (
 ) of \(\mathcal {M}\) and the additional types and constants for type class reasoning from Section 7.3. Our theories also need to contain a minimal set of axioms. The set
) of \(\mathcal {M}\) and the additional types and constants for type class reasoning from Section 7.3. Our theories also need to contain a minimal set of axioms. The set
 is an axiomatic basis for equality reasoning and will be explained in Section 7.2.
is an axiomatic basis for equality reasoning and will be explained in Section 7.2.
We will now discuss the inference system in three steps: the basic inference rules, equality and type class reasoning.
7.1 Basic Inference Rules
The axiom rule states that wellformed type-instances of axioms are provable:

where
 is a type substitution and
is a type substitution and
 denotes its application (see Section 4). The types substituted into the type variables need to be wellformed and conform to the sort constraint of the type variable:
denotes its application (see Section 4). The types substituted into the type variables need to be wellformed and conform to the sort constraint of the type variable:

The conjunction only needs to hold if
 actually changes something, i.e. if
actually changes something, i.e. if
 . This condition is not superfluous because otherwise
. This condition is not superfluous because otherwise
 and
and
 only hold if
only hold if
 is wellformed w.r.t
is wellformed w.r.t
 .
.
Note that there are no extra rules for general instantiation of type or term variables. Type variables can only be instantiated in the axioms. Term instantiation can be performed using the forall introduction and elimination rules.
The assumption rule allows us to prove terms already in the hypotheses:

Both
 and
and
 are characterized by introduction and elimination rules:
are characterized by introduction and elimination rules:




where
 .
.
7.2 Equality
Most rules about equality are not part of the inference system but are axioms (the set
 mentioned above). Consequences are obtained via the axiom rule.
mentioned above). Consequences are obtained via the axiom rule.
The first three axioms express that
 is reflexive, symmetric and transitive:
is reflexive, symmetric and transitive:

The next two axioms express that terms of type
 (
(
 and
and
 ) are equal iff they are logically equivalent:
) are equal iff they are logically equivalent:

The last equality axioms are congruence rules for application and abstraction:

Paulson [30] gives a slightly different congruence rule for abstraction, which allows to abstract over an arbitrary, free
 in
in
 . We are able to derive this rule in our inference system.
. We are able to derive this rule in our inference system.
Finally there are the lambda calculus rules. There is no need for
 conversion because
conversion because
 -equivalent terms are already identical thanks to the De Brujin indices for bound variables. For
-equivalent terms are already identical thanks to the De Brujin indices for bound variables. For
 and
and
 conversion the following rules are added. In contrast to the rest of this subsection, these are not expressed as axioms.
conversion the following rules are added. In contrast to the rest of this subsection, these are not expressed as axioms.


Rule (\(\beta \)) uses the substitution function
 as explained in Section 4 (and defined in the Appendix).
as explained in Section 4 (and defined in the Appendix).
Rule (\(\eta \)) requires a few words of explanation. We do not explicitly require that
 does not contain
does not contain
 . This is already a consequence of the precondition that
. This is already a consequence of the precondition that
 : it implies that
: it implies that
 is closed. For that reason it is perfectly unproblematic to remove the abstraction above
is closed. For that reason it is perfectly unproblematic to remove the abstraction above
 .
.
7.3 Type Class Reasoning
Wenzel [38] encoded class constraints of the form “type
 has class
has class
 ” in the term language as follows. There is a unary type constructor named
” in the term language as follows. There is a unary type constructor named
 and
and
 abbreviates
abbreviates
 . The notation
. The notation
 is short for
is short for
 where
where
 is the name of a new uninterpreted constant. You should view
is the name of a new uninterpreted constant. You should view
 as the term-level representation of type
as the term-level representation of type
 .
.
Next we represent the predicate “is of class
 ” on the term level. For this we define some fixed injective mapping
” on the term level. For this we define some fixed injective mapping
 from class to constant names. For each new class
from class to constant names. For each new class
 a new constant
a new constant
 of type
of type
 is added. The term
is added. The term
 represents the statement “type
represents the statement “type
 has class
has class
 ”. This is the inference rule deriving such propositions:
”. This is the inference rule deriving such propositions:

This is how the
 inference system is integrated into the logic.
inference system is integrated into the logic.
This concludes the presentation of \(\mathcal {M}\). We have shown some minimal sanity properties, incl. that all provable terms are of type
 and wellformed:
and wellformed:
Theorem 1

The attentive reader will have noticed that we do not require unused hypotheses in
 to be wellformed and of type
to be wellformed and of type
 . Similarly, we only require
. Similarly, we only require
 in rules that need it to preserve wellformedness of the terms and types involved. To restrict to wellformed theories and hypotheses we define a top-level provability judgment that requires wellformedness:
in rules that need it to preserve wellformedness of the terms and types involved. To restrict to wellformed theories and hypotheses we define a top-level provability judgment that requires wellformedness:

8 Proof Terms and Checker
Berghofer and Nipkow [4] added proof terms to Isabelle. We present an executable checker for these proof terms that is proved sound w.r.t. the above formalization of the metalogic. Berghofer and Nipkow also developed a proof checker but it was unverified and checked the generated proof terms by feeding them back through Isabelle’s unverified inference kernel.
It is crucial to realize that all we need to know about the proof term checker is the soundness theorem below. The internals are, from a soundness perspective, irrelevant, which is why we can get away with sketching them informally. This is in contrast to the logic itself, which acts like a specification, which is why we presented it in detail.
This is our data type of proof terms:

These proof terms are not designed to record proofs in our inference system, but to mirror the proof terms generated by Isabelle. Nevertheless, the constructors of our proof terms correspond roughly to the rules of the inference system.
 contains an axiom and a type substitution. This substitution is encoded as an association list instead of a function.
contains an axiom and a type substitution. This substitution is encoded as an association list instead of a function.
 and
and
 correspond to introduction of
correspond to introduction of
 and
and
 ,
,
 and
and
 correspond to the respective eliminations.
correspond to the respective eliminations.
 and
and
 relate to the assumption rule, where
relate to the assumption rule, where
 refers to a free assumption while
refers to a free assumption while
 contains a De Brujin index referring to an assumption added during the proof by an
contains a De Brujin index referring to an assumption added during the proof by an
 constructor.
constructor.
 denotes a proof that a type belongs to a given type class.
denotes a proof that a type belongs to a given type class.
Isabelle looks at terms modulo
 -equivalence and therefore does not save
-equivalence and therefore does not save
 or
or
 steps, while they are explicit steps in our inference system. Therefore we have no constructors corresponding to the (\(\beta \)) and (\(\eta )\) rules. The remaining equality axioms are naturally handled by the
steps, while they are explicit steps in our inference system. Therefore we have no constructors corresponding to the (\(\beta \)) and (\(\eta )\) rules. The remaining equality axioms are naturally handled by the
 constructor.
constructor.
In the rest of the section we discuss how to derive an executable proof checker. Executability means that the checker is defined as a set of recursive functions that Isabelle’s code generator can translate into one of a number of target languages, in particular its implementation language SML [5, 8, 9].
Because of the approximate correspondence between proof term constructors and inference rules, implementing the proof checker largely amounts to providing executable versions of each inference rule, as in LCF: each rule becomes a function that checks the side conditions, and if they are true, computes the conclusion from the premises given as arguments. The overall checker is a function

In particular we need to make the inductive wellformedness checks for sorts, types and terms, signatures and theories executable. Mostly, this amounts to providing recursive versions of inductive definitions and proving them equivalent.
We now discuss some of the more difficult implementation steps. To model Isabelle’s view of terms modulo
 -equivalence, we
-equivalence, we
 normalize our terms (
normalize our terms (
 -equivalence is for free thanks to De Brujin notation) during the reconstruction of the proof. A lengthy proof shows that this preserves provability (we do not go into the details):
-equivalence is for free thanks to De Brujin notation) during the reconstruction of the proof. A lengthy proof shows that this preserves provability (we do not go into the details):

Isabelle’s code generator needs some help handling the maps used in the (order-sorted) signatures. We provide a refinement of maps to association lists. Another problematic point is the definition of the type instance relation
 , which contains an (unbounded) existential quantifier. To make this executable, we provide an implementation which tries to compute a suitable type substitution. In another step, we refine the type substitution to an association list as well.
, which contains an (unbounded) existential quantifier. To make this executable, we provide an implementation which tries to compute a suitable type substitution. In another step, we refine the type substitution to an association list as well.
In the end we obtain a proof checker

that checks theory
 and checks if proof
and checks if proof
 proves the given proposition
proves the given proposition
 . The latter check is important because the Isabelle theorems that we check contain both a proof and a proposition that the theorem claims to prove. Function
. The latter check is important because the Isabelle theorems that we check contain both a proof and a proposition that the theorem claims to prove. Function
 checks this claim. As one of our main results, we can prove the correctness of our checker:
checks this claim. As one of our main results, we can prove the correctness of our checker:
Theorem 2

The proof itself is conceptually simple and proceeds by induction over the structure of proof terms. For each proof constructor we need to show that the corresponding inference rule leads to the same conclusion as its functional version used by
 . Most of the proof effort goes into a large library of results about terms, types, signatures, substitutions, wellformedness etc. required for the proof, most importantly the fact that
. Most of the proof effort goes into a large library of results about terms, types, signatures, substitutions, wellformedness etc. required for the proof, most importantly the fact that
 normalization preserve provability.
normalization preserve provability.
9 Size and Structure of the Formalization
All material presented so far has been formalized in Isabelle/HOL. The definition of the inference system (incl. types, terms etc.) resides in a separate theory
 that depends only on the basic library of Isabelle/HOL. It takes about 300 LOC and is fairly high level and readable – we presented most of it. This is at least an order or magnitude smaller than Isabelle’s inference kernel (which is not clearly delineated) – of course the latter is optimized for performance. Its abstract type of theorems alone takes about 2,500 LOC, not counting any infrastructure of terms, types, unification etc.
that depends only on the basic library of Isabelle/HOL. It takes about 300 LOC and is fairly high level and readable – we presented most of it. This is at least an order or magnitude smaller than Isabelle’s inference kernel (which is not clearly delineated) – of course the latter is optimized for performance. Its abstract type of theorems alone takes about 2,500 LOC, not counting any infrastructure of terms, types, unification etc.
The whole formalization consists of 10,000 LOC. The main components are:
-
Almost half the formalization (4,700 LOC) is devoted to providing a library of operations on types and terms and their properties. This includes, among others, executable functions for type checking, different types of substitutions, abstractions, the wellformedness checks and
 and
and
 reductions.
reductions. -
Proving derived rules of our inference system takes up 3,000 LOC. A large part of this is deriving rules for equality and the
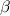 and
and
 reductions. Weakening rules are also derived.
reductions. Weakening rules are also derived. -
Making the wellformedness checks for (order-sorted) signatures and theories as well as the type instance checks executable takes 1,800 LOC.
-
Definition and correctness proof for the checker builds on the above material and take only about 500 additional LOC.
10 Integration with Isabelle
As explained above, Isabelle generates SML code for the proof checker. This code has its own definitions of types, terms etc. and needs to be interfaced with the corresponding data structures in Isabelle. This step requires 150 lines of handwritten SML code (glue code) that translates Isabelle’s data structures into the corresponding data structures in the generated proof checker such that we can feed them into
 . We cannot verify this code and therefore aim to keep it as small and simple as possible. This is the reason for the previously mentioned intentional implementation bias we introduced in our formalization. We describe now how the various data types are translated. We call a translation trivial if it merely replaces one constructor by another, possibly forgetting some information.
. We cannot verify this code and therefore aim to keep it as small and simple as possible. This is the reason for the previously mentioned intentional implementation bias we introduced in our formalization. We describe now how the various data types are translated. We call a translation trivial if it merely replaces one constructor by another, possibly forgetting some information.
The translation of types and terms is trivial as their structure is almost identical in the two settings. For Isabelle code experts it should be mentioned that the two term constructors Free and Var in Isabelle (which both represent free variables but Var can be instantiated by unification) are combined in type
 of the formalization which we left unspecified but which in fact looks like this:
of the formalization which we left unspecified but which in fact looks like this:
 . This is purely to trivialize the glue code, in our formalization
. This is purely to trivialize the glue code, in our formalization
 is totally opaque.
is totally opaque.
Proof term translation is trivial except for two special cases. Previously proved lemmas become axioms in the translation (see also below) and so-called “oracles” (typically the result of unfinished proofs, i.e. “sorry” on the user level) are rejected (but none of the theories we checked contain oracles). Also remember that the translation of proofs is not safety critical because all that matters is that in the end we obtain a correct proof of the claimed proposition.
We also provide functions to translate relevant content from the background theory: axioms and (order-sorted) signatures. This mostly amounts to extracting association lists from efficient internal data structures. Translating the axioms also involves translating some alternative internal representation of type class constraints into their standard form presented in Sect. 7.3.
The checker is integrated into Isabelle by calling it every time a new named theorem has been proved. The set of theorems proved so far is added to the axiomatic basis for this check. Cyclic dependencies between lemmas are ruled out by this ordering because every theorem is checked before being added to the axiomatic basis. However, an explicit cyclicity check is not part of the formalization (yet), which speaks only about checking single proofs.
11 Running the Proof Checker
We run this modified Isabelle with our proof checker on multiple theories in various object logics contained in the Isabelle distribution. A rough overview of the scope of the covered material for some logics and the required running times can be found in the following table. The running times are the total times for running Isabelle, not just the proof checking, but the latter takes 90% of the time. All tests were performed on a Intel Core i7-9750H CPU running at 2.60GHz and 32GB of RAM.
Logic | LOC | Time |
|---|---|---|
FOL | 4,500 | 45 secs |
ZF | 55,000 | 25 mins |
HOL | 10,000 | 26 mins |
We can check the material in several smaller object logics in their entirety. One of the larger such logics is first-order logic (FOL). These logics do not develop any applications but FOL comes with proof automation and theories testing that automation, in particular Pelletier’s collection of problems that were considered challenges in their day [32]. Because the proofs are found automatically, the resulting proof terms will typically be quite complex and good test material for a proof checker.
The logic ZF (Zermelo-Fraenkel set theory) builds on FOL but contains real applications and is an order of magnitude larger than FOL. We are able to check all material formalized in ZF in the Isabelle distribution.
Isabelle’s most frequently used and largest object logic is HOL. We managed to check about 12% of the Main library. This includes the basic logic and the libraries of sets, functions, orderings, lattices and groups. The formalizations are non-trivial and make heavy use of Isabelle’s type classes.
Why can we check about five times as many lines of code in ZF compared to HOL? Profiling revealed that the proof checker spends a lot of time in functions that access the signature, especially the wellformedness checks. The primary reasons: inefficient data structures (e.g. association lists) and thus the running time depends heavily on size of signature and increases with every new constant, type and class. To make matters worse, there is no sharing of any kind in terms/types and their wellformedness checks. Because ZF is free of polymorphism and type classes, these wellformedness checks are much simpler.
12 Trust Assumptions
We need to trust the following components outside of the formalization:
-
The verification (and code generation) of our proof checker in Isabelle/HOL. This is inevitable, one has to trust some theorem prover to start with. We could improve the trustworthiness of this step by porting our proofs to the verified HOL prover by Kumar et el. [13] but its code generator produces CakeML [14], not SML.
-
The unverified glue code in the integration of our proof checker into Isabelle (Sect. 10).
Because users currently cannot examine Isabelle’s internal data structures that we start from, they have to trust Isabelle’s front end that parses and transforms some textual input file into internal data structures. One could add a (possibly verified) presentation layer that outputs those internal representations into a readable format that can be inspected, while avoiding the traps Adams [3] is concerned with.
13 Future Work
Our primary focus will be on scaling up the proof checker to not just deal with all of HOL but with real applications (including itself!). There is a host of avenues for exploration. Just to name a few promising directions: more efficient data structures than association lists (e.g. via existing frameworks [19, 20]); caching of wellformedness checks for types and terms; exploiting sharing within terms and types (tricky because our intentionally simple glue code creates copies); working with the compressed proof terms [5] that Isabelle creates by default instead of uncompressing them as we do now.
We will also upgrade the formalization of our checker from individual theorems sets of theorems, explicitly checking cyclic dependencies (which are currently prevented by the glue code, see Sect. 10).
A presentation layer as discussed in Sect. 12 would not just allow the inspection of the internal representation of the theories but could also be extended to the proofs themselves, thus permitting checkers to be interfaced with Isabelle on a textual level instead of internal data structures.
It would also be nice to have a model-theoretic semantics for \(\mathcal {M}\). We believe that the work by Kunčar and Popescu [15,16,17,18] could be adapted from HOL to \(\mathcal {M}\). This would in particular yield semantically justified cyclicity checks for constant and type definitions which we currently treat as axioms because a purely syntactic justification is unclear.
References
Åman Pohjola, J., Gengelbach, A.: A mechanised semantics for HOL with ad-hoc overloading. In: Albert, E., Kovács, L. (eds.) LPAR 2020: 23rd International Conference on Logic for Programming, Artificial Intelligence and Reasoning. EPiC Series in Computing, vol. 73, pp. 498–515. EasyChair (2020), https://doi.org/10.29007/413d
Abrahamsson, O.: A verified proof checker for higher-order logic. J. Log. Algebraic Methods Program. 112, 100530 (2020), https://doi.org/10.1016/j.jlamp.2020.100530
Adams, M.: HOL Zero’s solutions for Pollack-inconsistency. Lect. Notes in Comp. Sci., vol. 9807, pp. 20–35. Springer (2016), https://doi.org/10.1007/978-3-319-43144-4_2
Berghofer, S., Nipkow, T.: Proof terms for simply typed higher order logic. In: Harrison, J., Aagaard, M. (eds.) Theorem Proving in Higher Order Logics. Lect. Notes in Comp. Sci., vol. 1869, pp. 38–52. Springer (2000)
Berghofer, S., Nipkow, T.: Executing higher order logic. In: Callaghan, P., Luo, Z., McKinna, J., Pollack, R. (eds.) Types for Proofs and Programs (TYPES 2000). Lect. Notes in Comp. Sci., vol. 2277, pp. 24–40. Springer (2002)
Carneiro, M.M.: Metamath Zero: Designing a theorem prover prover. In: Benzmüller, C., Miller, B.R. (eds.) Intelligent Computer Mathematics, CICM 2020. Lect. Notes in Comp. Sci., vol. 12236, pp. 71–88. Springer (2020), https://doi.org/10.1007/978-3-030-53518-6_5
Gheri, L., Popescu, A.: A formalized general theory of syntax with bindings: Extended version. J. Automated Reasoning 64(4), 641–675 (2020), https://doi.org/10.1007/s10817-019-09522-2
Haftmann, F., Krauss, A., Kunčar, O., Nipkow, T.: Data refinement in Isabelle/HOL. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) Interactive Theorem Proving (ITP 2013). Lect. Notes in Comp. Sci., vol. 7998, pp. 100–115. Springer (2013)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) Functional and Logic Programming (FLOPS 2010). Lect. Notes in Comp. Sci., vol. 6009, pp. 103–117. Springer (2010)
Haftmann, F., Wenzel, M.: Constructive type classes in isabelle. In: Altenkirch, T., McBride, C. (eds.) Types for Proofs and Programs, TYPES 2006. Lect. Notes in Comp. Sci., vol. 4502, pp. 160–174. Springer (2006), https://doi.org/10.1007/978-3-540-74464-1_11
Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) Proceedings of the third International Joint Conference, IJCAR 2006. Lect. Notes in Comp. Sci., vol. 4130, pp. 177–191. Springer, Seattle, WA (2006)
Hurd, J.: OpenTheory: Package management for higher order logic theories. In: Reis, G., Théry, L. (eds.) Workshop on Programming Languages for Mechanized Mathematics Systems (ACM SIGSAM PLMMS 2009). pp. 31–37 (2009)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: Self-formalisation of higher-order logic — semantics, soundness, and a verified implementation. J. Automated Reasoning 56(3), 221–259 (2016), https://doi.org/10.1007/s10817-015-9357-x
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: A verified implementation of ML. In: Principles of Programming Languages (POPL). pp. 179–191. ACM Press (Jan 2014), https://doi.org/10.1145/2535838.2535841
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. In: Urban, C., Zhang, X. (eds.) Interactive Theorem Proving, ITP 2015. Lect. Notes in Comp. Sci., vol. 9236, pp. 234–252. Springer (2015), https://doi.org/10.1007/978-3-319-22102-1_16
Kunčar, O., Popescu, A.: Comprehending Isabelle/HOL’s consistency. In: Yang, H. (ed.) Programming Languages and Systems, ESOP 2017. Lect. Notes in Comp. Sci., vol. 10201, pp. 724–749. Springer (2017), https://doi.org/10.1007/978-3-662-54434-1_27
Kunčar, O., Popescu, A.: Safety and conservativity of definitions in HOL and Isabelle/HOL. Proc. ACM Program. Lang. 2(POPL), 24:1–24:26 (2018), https://doi.org/10.1145/3158112
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. J. Automated Reasoning 62(4), 531–555 (2019), https://doi.org/10.1007/s10817-018-9454-8
Lammich, P., Lochbihler, A.: The Isabelle collections framework. In: Kaufmann, M., Paulson, L.C. (eds.) Interactive Theorem Proving, ITP 2010. Lect. Notes in Comp. Sci., vol. 6172, pp. 339–354. Springer (2010), https://doi.org/10.1007/978-3-642-14052-5_24
Lochbihler, A.: Light-weight containers for isabelle: Efficient, extensible, nestable. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) Interactive Theorem Proving, ITP 2013. Lect. Notes in Comp. Sci., vol. 7998, pp. 116–132. Springer (2013), https://doi.org/10.1007/978-3-642-39634-2_11
Journal of Automated Reasonig: Special Issue: Theory and Applications of Abstraction, Substitution and Naming, vol. 49. Springer (Aug 2012), https://link.springer.com/journal/10817/volumes-and-issues/49-2
Nipkow, T.: Order-sorted polymorphism in Isabelle. In: Huet, G., Plotkin, G. (eds.) Logical Environments. pp. 164–188. Cambridge University Press (1993)
Nipkow, T.: More Church-Rosser proofs (in Isabelle/HOL). J. Automated Reasoning 26, 51–66 (2001)
Nipkow, T., Klein, G.: Concrete Semantics with Isabelle/HOL. Springer (2014), http://concrete-semantics.org
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Nipkow, T., Paulson, L.C.: Isabelle-91. In: Kapur, D. (ed.) Automated Deduction - CADE-11. Lect. Notes in Comp. Sci., vol. 607, pp. 673–676. Springer (1992), https://doi.org/10.1007/3-540-55602-8_201
Nipkow, T., Prehofer, C.: Type reconstruction for type classes. J. Functional Programming 5(2), 201–224 (1995)
Nipkow, T., Roßkopf, S.: Isabelle’s metalogic: Formalization and proof checker. Archive of Formal Proofs (Apr 2021), https://isa-afp.org/entries/Metalogic_ProofChecker.html, Formal proof development
Nipkow, T., Snelting, G.: Type classes and overloading resolution via order-sorted unification. In: Hughes, J. (ed.) Proc. 5th ACM Conf. Functional Programming Languages and Computer Architecture. Lect. Notes in Comp. Sci., vol. 523, pp. 1–14. Springer (1991)
Paulson, L.C.: The foundation of a generic theorem prover. J. Automated Reasoning 5, 363–397 (1989)
Paulson, L.C. (ed.): Isabelle. LNCS, vol. 828. Springer, Heidelberg (1994). https://doi.org/10.1007/BFb0030541
Pelletier, F.: Seventy-five problems for testing automatic theorem provers. J. Automated Reasoning 2, 191–216 (06 1986), https://doi.org/10.1007/BF02432151
Pfenning, F.: Elf: A language for logic definition and verified metaprogramming. In: Logic in Computer Science (LICS 1989). pp. 313–322. IEEE Computer Society Press (1989)
Pfenning, F., Schürmann, C.: System description: Twelf - A meta-logical framework for deductive systems. In: Ganzinger, H. (ed.) Automated Deduction, CADE-16. Lect. Notes in Comp. Sci., vol. 1632, pp. 202–206. Springer (1999), https://doi.org/10.1007/3-540-48660-7_14
Pientka, B.: Beluga: Programming with dependent types, contextual data, and contexts. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) Functional and Logic Programming, FLOPS 2010. Lect. Notes in Comp. Sci., vol. 6009, pp. 1–12. Springer (2010), https://doi.org/10.1007/978-3-642-12251-4_1
Sozeau, M., Boulier, S., Forster, Y., Tabareau, N., Winterhalter, T.: Coq Coq correct! Verification of type checking and erasure for Coq, in Coq. Proc. ACM Program. Lang. 4(POPL), 8:1–8:28 (2020), https://doi.org/10.1145/3371076
Urban, C.: Nominal techniques in Isabelle/HOL. J. Automated Reasoning 40, 327–356 (2008), https://doi.org/10.1007/s10817-008-9097-2
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A.P. (eds.) Theorem Proving in Higher Order Logics, TPHOLs’97. Lect. Notes in Comp. Sci., vol. 1275, pp. 307–322. Springer (1997), https://doi.org/10.1007/BFb0028402
Acknowledgements
We thank Kevin Kappelmann, Magnus Myreen, Larry Paulson, Andrei Popescu, Makarius Wenzel and the anonymous reviewers for their comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix
A Appendix





Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Nipkow, T., Roßkopf, S. (2021). Isabelle’s Metalogic: Formalization and Proof Checker. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)





 there must be a
there must be a
 for every superclass
for every superclass
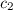 of
of
 and b) coregularity which guarantees the existence of principal types [
and b) coregularity which guarantees the existence of principal types [

 :
:
 where
where

 and
and
 reductions.
reductions.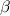 and
and
 reductions. Weakening rules are also derived.
reductions. Weakening rules are also derived.