Keywords

1 Introduction

The vertebral motor unit is, as for every part of the body, exposed to the possibility of degenerative pathologies, a natural process of global aging of the osteo-ligamentous structures of the vertebral column, and/or traumatic and congenital pathologies, such as to cause a structural disorder. In cases of pathologies in which results are not obtained using corrective aids or with physiotherapy, an intervention, known as pedicle arthrodesis, is indispensable. In particular, arthrodesis of the lumbar vertebrae is a surgical technique that allows to join bones in the lumbar spine to stabilize it in order to reduce pain or deformity. Experience shows that the clinical aid that best allows to guide the screws in the spinal fusion surgery with extreme precision is the use of a surgical mask [1,2,3,4], a vertebral drilling template designed for delicate pedicle arthrodesis operations. The surgical device allows to implant the screws in the vertebral tracts of interest with extreme safety and precision; the result is a substantial appreciable decrease in operating times (about 40%) and a massive reduction in the harmful ionizing radiation (about 80%) due to the X-ray control so far essential to perform the intervention [5, 6].

The templates, customized for individual patients, are designed according to the most modern CAD technologies and made thanks to 3D printing in bio-compatible material [7]. A normal pedicle arthrodesis operation requires that the screws must be inserted by previously making two suitably positioned holes on the vertebra which, as a rule, pass through the pedicles and are fixed in the vertebra body. Vertebra fixation is the most complex phase for this type of operation; it can be compromised by human error, morphology and cleaning of the vertebra, as extremely delicate tissues and structures are present in the intervention area which, if compromised, also cause irreversible damage to the patient. The solution to this problem consists in the design and construction of a “custom made” template for vertebral surgery, customized and optimized for the individual patient, aimed at the directional drilling of the vertebrae with a structure characterized by two hollow cylindrical geometry guides that have the function of guide the tip of the surgical drilling tool so that the hole is drilled in the position chosen in the pre-operative phase by the surgeon. Although the area to be operated is “clean”, as the surgical team is preparing for a skeletal phase of the affected section, blood spills are inevitable throughout the intervention phase. This causes instability due to the positioning of the drilling mask on the vertebral surface due to the presence of superficial and deep muscle tissues and bundles affecting the area to be operated. The solution to this problem could be to design a template whose geometric profile perfectly follows the shape of the vertebral body on which it concerns. The presence of undercuts that can be found in the anchorage areas of the template can cause, however, problems during the insertion and extraction phase of the same. This type of problem is very similar to that encountered in the manufacture of molds in industrial processes. The mold must generally be designed without cavities that can limit the extraction of the piece: in particular, undercuts must be avoided, i.e. angles less than 90°, which, in fact, make the molded element indivisible from the mold. The parts of the model that during the extraction would ruin the shape are said to be undercut. The extraction of the model is possible only in the absence of undercuts, i.e. all those areas of the model that are in the shadow of the direction of extraction of the model itself. Multiple systems of automatic undercut recognition are now consolidated, according to the geometry to be obtained by means of the mold, starting from three-dimensional CAD models [8,9,10,11,12,13].

None of these methods, however, has ever been used so far for the design of such surgical devices, leading over time to neglect the problem of undercuts in vertebral drilling templates, focusing on design requirements, such as the direction of screw centering. The aim of this work, instead, is to dwell on the problems resulting from the use of the device, during the insertion and extraction phases, ensuring precision and maintenance of the positioning at the same time. This is possible through the implementation of an algorithm capable of eliminating the undercuts on the vertebra-template interaction surface, evaluating the uniqueness of positioning and the stability. The vertebra-template coupling is even more stable as the contact surface is extended. Thinking of creating a profile of the template that fully matches that of the spinous process would, however, lead to evident problems in the phase of fixing the template on the vertebra as well as in the phase of extraction of the same. Furthermore, carefully analysing the morphology of a lumbar vertebra, it can be noticed that the major surface irregularities are those affecting the spinous process. Imagining, therefore, to position the drilling mask on the vertebra, the undercut problems that are encountered are precisely those affecting the spinous process and the cavity obtained inside the central body of the template. In this regard, it is not immediate to define the correct extraction directions for the model, given that the undercuts present could prevent more than one. The design and subsequent construction of a template is, therefore, bound by the extraction direction established during the design phase. The problem is, however, that by bypassing the undercuts, contact surfaces are eliminated, reducing stability. It is important to evaluate the optimal extraction direction taking also into account the stability.

The aim of this work was to implement a corrective semi-automatic model that, after identifying the presence of any undercuts, is able to modify the anchoring profile of the template according to the extraction direction, to determine its final contact surface and its stability. The profile of the template, therefore, will be that of a ‘perfectly matching’ geometry with the spinous process, subtracted, however, from the relevant undercuts. In this way, it will be possible to position and extract the model from the vertebra without difficulty, without affecting any effect on stability, due to a smaller contact surface.

2 Methodology

For the generation of the template, a specific methodology has been implemented, aimed at optimizing the conditions of insertability, stability and uniqueness of positioning, which maximize the use of the device during the operating phase. The pursued methodology provided for the succession of a series of procedural steps, listed below:

  • Using a medical image processing software (3DSlicer, slicer.org), a three dimensional surface, in.STL format, related to the spinous process of a lumbar vertebra has been obtained, and the part of the surface of the spinous process on which the template rests is duplicated.

  • One of the infinite possible extraction directions has been identified. As the extraction direction changes, undercuts located in different positions will occur. Note how the insertion and extraction of the template take place in the same direction, only the orientation changes, so in the two operations the same shaded areas are found.

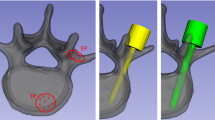
  • To identify the undercuts obtained for an assigned direction, the scalar product was calculated between the normal vectors and the extraction direction chosen, according to the traditional convexity approach method. The outlines of the undercut areas have been grouped (Fig. 1).

Fig. 1.
figure 1

Identification of undercut areas, highlighted in the square regions, according to the chosen extraction direction (highlighted in the circle).

Full size image

  • A new reference system was then adopted, in order to align the z axis with the extraction direction and orientation, for all the vertices of the undercut areas.

  • We proceeded with the analysis of the logics used to modify the vertices of all the triangles representative of the shadow areas found during the extraction. This modification takes place in correspondence with the control points, which, delimiting the previously highlighted regions, are not subject to change in the implementation of the algorithm. In particular, starting from the analysis of vertices with the highest value of z coordinate, the following cases may occur:

    • Case 1: the node belongs to a triangle where the other two nodes are on the contour. It will be necessary to move this node perpendicular to the segment joining the two nodes of the contour;

    • Case 2: the node belongs to two triangles that have two nodes on the contour. If the triangles are adjacent, the node must be aligned with the common one;

    • Case 3: the node belongs to a triangle with a node on the contour, proceed as in Case1 but you have to move the segment holding the node still;

    • Case 4: the node belongs to two adjacent triangles with a node on the contour, the node must be aligned with the node on the contour (same x-y coordinates in the new system);

  • The algorithm outputs a cloud of points representing the new profile of the template that facilitates its extraction and that at the same time guarantees its insertion. It represents the first mandatory condition for the realization of the template and is verified respecting the criterion of minimum interference.

  • The stability condition is assessed from the transverse contact surface. By the calculation of the contact surface between the template and the vertebra, starting from an extraction direction, its perpendicular is considered and the inclination of the normal at each triangle is evaluated with respect to the extraction direction itself. The contact surface is then projected onto a plane containing the extraction direction, choosing the criterion of maximum stability as that which minimizes the projection area. The process is repeated for all possible extraction directions, covering interactions of 360°, comparing the average stability assessed between each degree interval and another. The extraction direction will therefore be the one for which the minimum resistance condition occurs.

  • The ideal condition of the uniqueness of positioning is that for which the maximum contact surface is guaranteed. Therefore, the extraction direction will be chosen such that, due to the removal of the undercuts, the minimum subtraction of the contact area between the dima and vertebra is obtained. The final execution of this iterative method leads to the generation of a template model (Fig. 2), optimized by maximizing the objective function:

    $$ {\mathbf{F}}.{\mathbf{O}}.\, = \,{\mathbf{max}}\left( {{\mathbf{contact}}\,{\mathbf{surface}}\, + \,{\mathbf{min}}\left( {{\mathbf{transverse}}\,{\mathbf{projection}}\,{\mathbf{surface}}} \right)} \right). $$
Fig. 2.
figure 2

Three-dimensional template model before the undercut removal method (to the left) and after its application (to the right). Regions of the modified undercuts are highlighted in the red areas.

Full size image

3 Conclusion

In this work, a solution was found to the problem of interference, represented by the so-called shaded areas, present when inserting a template for vertebral drilling along a generic direction; the problems encountered concern the positioning of the template on the vertebral surface. These limits are mainly related to the presence of undercuts, i.e. those areas of the spinous process which, brought back into the cavity of the model body, entail complications at the time of extraction. The problem of undercuts has been limited in the present work by reducing the contact surface of the prototype with that of the spinous process. The procedure here presented allows to modify the geometric profile of the vertebral template according to the extraction direction chosen, and to compare different directions with each other, in order to identify the best solution that can, on the one hand, overcome the impediments of extraction caused by the undercuts and, on the other hand, guarantee the maximum possible adherence, compensating for the problem of stability and for the identification of a unique positioning.