Quantum Effects in Cold and Controlled Molecular Dynamics

Abstract

This chapter discusses three examples of quantum effects that can be observed in state-of-the-art experiments with molecular beams—scattering resonances as a probe of interparticle interactions in cold collisions, the protection of Fano-Feshbach resonances against decay despite resonant coupling to a scattering continuum, and a circular dichroism in photoelectron angular distributions arising in the photoionization of randomly oriented chiral molecules. The molecular beam setup provides molecules in well-defined quantum states. This, together with a theoretical description based on first principles, allows for excellent agreement between theoretical prediction and experimental observation and thus a rigorous understanding of the observed quantum effects.

1 Introduction

When you ask young students entering a university physics course today for the term they associate most with quantum mechanics, many of them will respond with “entanglement”. This reflects the rise of quantum information science out of an often ridiculed ivory tower to the decision-making levels of the big tech companies and to the headlines of well-respected media outlets. In the waves of excitement created by the “second quantum revolution” [1, 2], it may be overlooked that features more traditionally associated with quantum mechanics continue to fascinate and challenge our classically trained intuition.

This chapter reviews three examples of such quantum effects beyond entanglement from recent work of my group—tunneling resonances that emerge in cold collisions and that can be used to probe interparticle interactions [3], Fano-Feshbach resonances that can be protected against decay by a suitable phase condition [4], and quantum pathway interference in the circular dichroism of photoelectrons that is observed after the photoionization of chiral molecules [5, 6]. All three examples share a rigorous theoretical description based on first principles. More importantly for the present contribution, the quantum effects discussed here have been observed in experiments with molecular beams [3, 4, 7]. They thus testify to the topicality and continuing significance of the molecular beam technique developed by Otto Stern and colleagues.

2 Quantum Scattering Resonances in Cold Collisions

The wave nature of colliding particles emerges most prominently at low scattering energies [8, 9], where quantum resonances dominate the scattering cross section before threshold laws take over [10]. While quantum resonances are also present at higher scattering energies, this presence is hidden in the ensemble average over all quantum states that are populated at a given energy. In other words, collisions are “cold” when only a few partial waves contribute to the scattering cross section [8]. At the corresponding collision energies, the dynamics are often dominated by the long-range behavior of the interparticle interactions [10], easing the interpretation of the collision studies.

In order to observe quantum scattering resonances experimentally, one needs to ensure a sufficiently narrow velocity distribution—narrower than the resonance width—in addition to the capability to finely tune the relative kinetic energy of the colliding particles to very low values. Both requirements can be met with merged neutral beams [11, 12], the use of which has allowed for the observation of tunneling resonances in Penning ionization reactions [13]. Since then, scattering resonances have also been observed in inelastic low-energy collisions, see Ref. [14] and references therein.

Fig. 1

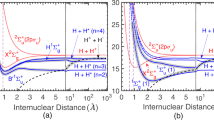
Tunneling, or shape, resonances (top) versus Fano-Feshbach resonances (bottom): Tunneling resonances form on a single potential curve displaying a barrier. In contrast, Fano-Feshbach resonances arise from the coupling of scattering states to a bound state belonging to another scattering channel which is energetically closed and asymptotically characterized by a different set of quantum numbers. In both cases, scattering amplitude gets trapped at short interparticle distance

Penning ionization reactions occur when the excitation energy of a particle prepared in a metastable quantum state is sufficient to ionize its collision partner [15]. Metastable nobel gas atoms, for example, feature excitation energies of more than 10 eV which is above the ionization potential of most molecules. The scattering resonances in this case are tunneling, or shape, resonances that occcur when the kinetic energy of the colliding particles matches the energy of a quasi-bound state that is trapped behind the rotational barrier of an otherwise barrier-less potential, cf. Fig. 1. Peaks in the ionization cross section indicate not only the presence of a tunneling resonance but also highlight the corresponding quantization of the intermolecular motion. In a more pictorial description, when the colliding particles hit a resonance upon tunneling through the rotational barrier, their amplitude gets trapped at short interparticle distances. This results in peaks in the cross section since the ionization probability grows inverse-exponentially with interparticle distance [15].

The experiments leading to the first observation of tunneling resonances in Penning ionization reactions were carried out with metastable helium colliding with argon atoms and dihydrogen molecules [13]. At the time, no qualitative difference was observed for the Penning ionization of an atom compared to that of a molecule. In general, however, one would expect the molecular degrees of freedom—rotations or vibrations—as well as the anisotropy of the interparticle interaction potential (the difference between the molecule hitting the metastable atom head-on or in a T-shaped geometry) to come into play and modify the cross section, respectively the reaction rate. For low-energy collisions involving dihydrogen molecules, a change of the H$_2$ vibrational state is energetically not accessible. In order to assess the role of the anisotropy of the interparticle interaction, it is useful to expand the angular dependence of the interaction potential into Legendre polynomials,

$$ V(R,\theta )=V_0(R) + V_2(R)\cos ^2\theta + \cdots . $$

Here, R and $\theta$ denote the interparticle separation and the angle between intermolecular axis and collision axis, respectively. A comparison of the magnitude of $V_2(R)$ to the rotational constant of the molecule yields, for H$_2$, energy equivalents of 1 K versus roughly 200 K. The collision is thus highly unlikely to induce changes of the rotational state. Nevertheless, the anisotropy of the interaction does affect the reaction rate! It determines the occurrence of quantum scattering resonances in slow barrier-less reactions [3] and dictates the scaling of the reaction rate coefficient with collision energy in fast barrier-less reactions [16].

The role of the anisotropy for the occurence of quantum scattering resonances is most readily understood using an adiabatic separation of interparticle motion and internal molecular rotation [17]. Denoting the eigenstates of the internal molecular rotation by $|j,m_j\rangle$, the potential energy operator is effectively diagonal in this basis (reflecting the absence of rotational state changing collisions), but the diagonal matrix elements differ for $j=0$ and $j=1$: While the matrix element for $j=0$ contains only the isotropic part of the interaction, $V_0(R)$, those for $j=1$ also depend on the anisotropy, $V_2(R)$. This allows one to directly probe the role of the anisotropy in atom-molecule collisions via quantum scattering resonances [3], provided the molecule can be selectively prepared in $j=0$ or $j=1$.

Rotational state selection in H$_2$ molecules is made possible by the large rotational splitting together with the nuclear spin symmetry. The latter implies that para-H$_2$ must have an even rotational wavefunction, thus $j=0$, whereas the rotational wavefunctions for ortho-H$_2$ are odd, i.e., $j=1$ for ortho-dihydrogen. Higher rotational levels are not populated in molecular beam experiments due to the large rotational splitting. Samples of almost pure para-H$_2$ are readily obtained by catalytic ortho-para conversion. It is thus comparatively straightforward to carry out molecular beam studies with rotational state selection [3, 16].

Fig. 2

Adapted from Ref. [3]

Rate coefficient for Penning ionization of dihydrogen colliding with metastable helium: The tunneling resonance at a collision energy of k$_B\times 270\,$mK appears only if the molecule is rotationally excited. This is due to the anisotropy of the interparticle interaction (equal to $V_2$ in leading order).

Repeating the Penning ionization experiments of Ref. [13] with dihydrogen molecules in a well defined rotational state led to the surprising observation, cf. Fig. 2, of the low-energy resonance (at a collision energy of k$_B\times 270\,$mK) occuring only for ortho-H$_2$, i.e., only for rotationally excited molecules. A theoretical model capturing this phenomenon requires spectroscopic accuracy. Systematic corrections to high-level state-of-the-art quantum chemistry combined with coupled channels calculations allow for reaching this accuracy. This is illustrated by the green, blue and red curves in Fig. 2, depicting the results obtained with a potential energy surface derived by coupled cluster theory with single, double and non-iterative triple excitations (green), including the full CI correction (blue) and further improved by uniformly scaling the correlation energy by 0.4% (red) [3].

The excellent agreement between the theoretical results and the experimental data observed in Fig. 2 allows for a more indepth examination of the role of the anisotropy. In the theoretical model, we can easily modify the relative weight of the anisotropic part of the interaction potential, denoted by $\alpha$ in Fig. 2. Increasing $\alpha$ up to 50% does not introduce a noticeable change on the results obtained with para-H$_2$, i.e., molecules in their rotational ground state [3]. On the other hand, the low-energy resonance observed only for rotationally excited H$_2$ in Fig. 2 depends very sensitively on the scaling factor of the anisotropic potential, shifting to lower energies with decreasing anisotropy [3].

The reason underlying this behavior can be unveiled using the adiabatic approximation mentioned above [17]. As is often the case with perturbation theory, it does not yield a quantitative description but qualitatively provides the correct picture. When examining the adiabatically separated scattering channels, a bound state just below the dissociation threshold occurs for rotational ground state para-dihydrogen (with $\ell =3$, $j=0$, and $J=3$). For rotationally excited ortho-dihydrogen, the anisotropic part of the interparticle interaction potential introduces an energy shift that is added to the effective potential. This pushes, what is a weakly bound state for para-dihydrogen, above the dissociation threshold for ortho-dihydrogen, turning the bound state into a shape resonance (with $\ell =3$, $j=1$, and $J=3$) [3], thus solving the riddle of resonance (dis)appearance.

To conclude this section, quantum scattering resonances testify to the emergence of the wave nature of matter in “cold” collisions. Using dihydrogen molecules in merged beam studies allows for simple rotational state selection which in turn can be used to probe the anisotropic part of the interparticle interaction governing Penning ionization reactions [3, 16]. While an excellent agreement between theory and experiment can be reached when including appropriate corrections for electron correlations, the calculation of quantum resonances involving metastable states continues to present a significant challenge even for the highest available levels of first principles based theory.

3 Phase-Protection in Fano-Feshbach Resonances

After understanding the dramatic effects that very small shifts in energy may have on a shape resonance, in the present section, another type of quantum resonance will highlight the sensitivity of resonances to small changes in phase. A Fano-Feshbach resonance describes the decay of a bound quantum state due to coupling with a continuum of scattering states. In contrast to shape resonances, it involves two distinct scattering channels characterized by different quantum numbers, as sketched in Fig. 1. In the original theory, the coupling between bound and continuum states described an effective nucleon-nucleon interaction [18], resp. configuration interaction in autoionization [19]. In recent years, Fano-Feshbach resonances due to the hyperfine interaction between different nuclear spin states have attracted attention as key tool for control in ultracold gases [20]. The present example considers rovibrational predissociation resonances due to the spin-orbit interaction [21].

Predissociation resonances may be populated by associative ionization which accompanies a Penning ionization reaction, provided the dependence of the Penning ionization rate on interparticle separation matches the ionic potential energy curve [15]. The ionization then populates bound levels of noble gas diatomic molecules such as HeAr$^+$, NeAr$^+$, or HeKr$^+$ which may or may not be spin-excited. These seemingly simple molecules with very similar electronic structure possess (spin-excited) predissociation resonances with surprisingly different lifetimes.

In order to estimate lifetimes, one typically inspects the coupling responsible for the decay. When comparing predissociation in HeAr$^+$ and NeAr$^+$, the spin-orbit splitting $\Delta$ in the two cases is identical. The term dominating the coupling between spin-excited and ground states is radial coupling [4] which scales as $\Delta /\mu$, where $\mu$ is the reduced mass. The lifetime of the resonances then scales with $\mu ^2$. Since, for the two diatoms, the reduced masses differ by a factor of approximately four, the lifetime of NeAr$^+$ would be expected to be larger than that of HeAr$^+$ by about an order of magnitude. This expectation derived from scaling arguments ignores, however, a phase dependence of the lifetimes which may entirely alter the picture, as shown next.

A qualitative understanding of the resonance lifetimes can be obtained in first order perturbation theory, using Fermi’s golden rule:

$$\begin{aligned} \tau ^{-1}_\varphi \sim |\langle k_\mathrm {res}|\boldsymbol{\mathsf {{W}}}_\mathrm {coupl}|\varphi \rangle |^2\,, \end{aligned}$$

(1)

where $\left| {\varphi } \right\rangle$ denotes the quasi-bound state, $\boldsymbol{\mathsf {{W}}}_\mathrm {coupl}$ the coupling operator, and $\left| {k_\mathrm {res}} \right\rangle$ the continuum state with scattering momentum $k_\mathrm {res}$, in resonance with the quasi-bound state, cf. Fig. 1. Since the continuum state describes the scattering off a potential, a phase shift $\delta$ is associated with the position of the repulsive wall. It is this phase shift that determines the value of the complex overlap in Eq. (1). In particular, there exist combinations of k and $\delta$ for which the overlap vanishes such that $\tau _\varphi \rightarrow \infty$ despite non-zero coupling! We have termed this phenomenon “phase protection” [4]. In fact, it is straightforward to show that vanishing overlap is equivalent to

$$\begin{aligned} \mathrm {arg}\left( \tilde{\varphi }(k)\right) +\delta =m\pi \quad \mathrm {with}\,\;m\in \mathbb {Z} \end{aligned}$$

(2)

with $\tilde{\varphi }(k)$ the Fourier transform of the quasi-bound state, when neglecting the energy dependence of the phase shift $\delta$ and assuming s-wave scattering.

Fig. 3

Adapted from Ref. [4]

Potential energy curves (left), lifetimes (center), and resonance positions (right) of predissociation resonances in spin-excited noble gas dimers.

In a real molecule, the resonance lifetime will never strictly go to infinity since eventually other decay mechanisms will become relevant. However, the lifetime can indeed become very large. This is shown in Fig. 3 displaying the potential energy curves, derived from spectroscopic data, respectively coupled-cluster calculations, for HeAr$^+$ and NeAr$^+$, together with the lifetimes obtained with a complex absorbing potential and including relativistic and angular couplings [4]. The potential energy curves shown in the left-hand part of Fig. 3 highlight the similarity of the potential energy curves and spin-orbit coupling $\Delta$ for the two molecules. In contrast, a striking difference is observed in the middle panel of Fig. 3, where the predissociation lifetimes of spin-excited NeAr$^+$ span more than four orders of magnitude whereas those of HeAr$^+$ differ by only a factor of 10. This difference is rationalized in terms of the condition for phase protection, cf. Eq. (2), visualized in the right part of Fig. 3. The lines indicate the combinations of k (respectively scattering energy) and $\delta$ for which the overlap in Eq. (1) vanishes. For NeAr$^+$, several resonance positions are located very close to those lines. The closer the resonance position to its corresponding phase protection line, the larger becomes the corresponding lifetime. In contrast, for HeAr$^+$, none of the resonances fulfills even approximately the condition for phase protection which is why the lifetimes span a much smaller range.

Experimental evidence for the lifetimes of spin-excited NeAr$^+$ spanning several orders of magnitude is provided by two experiments [4], using molecular beams. First, velocity-map imaging (VMI) of the reaction products of Penning and associative ionization of argon by metastable helium revealed predissociation for HeAr$^+$ to occur on a timescale smaller than the time of flight of the VMI setup, of the order of $10\,\mu$s. In contrast, the predissociation feature was missing in the VMI for NeAr$^+$, suggesting lifetimes significantly larger than the time of flight [4]. A second experiment, designed to assess the range of NeAr$^+$ lifetimes more directly, injected the molecular ions generated by associative ionization into an electrostatic ion beam trap [22] and recorded oscillations of the molecules between two electrostatic mirrors for several hundreds of milliseconds via trap loss of neutral particles. The experimental data was found to decay non-exponentially, with decay times ranging from below $50\,\upmu$s up to 100 ms [4], in excellent agreement with the predictions of Fig. 3.

One may wonder whether there is a way to predict, for a given molecule, the chance of phase protection to occur. Assuming one can approximate the potential energy curve by a Morse potential, the lifetime of level v is determined by a phase and the Fourier transform of the corresponding eigenfunction, $\tilde{\psi }_v(k)$,

$$ \tau _v^{-1}\propto \sin \left( \delta + \phi _v(k)\right) ^2 \, \left| \tilde{\psi }_v(k) \right| ^2, $$

where $\phi _v(k) = \mathrm {arg}[\tilde{\psi }_v(k)]$. On top of a smooth variation with k (or energy) due to $\left| \tilde{\psi }_v(k)\right| ^2$, the lifetimes $\tau _v$ oscillate and vanish whenever the condition for phase protection, cf. Eq. (1), is fulfilled. In order to answer the question how often the latter will happen, one can exploit the fact that, for a Morse potential, $\tilde{\psi }_v(k)$ is known analytically, in terms of complex $\Gamma$-functions [23]. This allows for deriving the scaling of the lifetimes with the parameters of the Morse potential and the reduced mass: The number of times $\tau _v$ vanishes, and thus the chance for phase protection, increases with $\mu$ as well as the well depth and equilibrium distance and decreases with the potential width [4]. This agrees well with the observations for NeAr$^+$ and HeAr$^+$ in Fig. 3 since the reduced mass and the well depth are larger for NeAr$^+$ than for HeAr$^+$, while the position of the minimum and the potential width are very similar. Moreover, this scaling argument predicts an isotope effect on predissociation lifetimes which has indeed been observed experimentally for N$_2^+\,\,$ [24] and Ne$_2^+$ [25].

To summarize this section, phase protection refers to the fact that the lifetime of a quasi-bound quantum state can become very, very large despite non-zero coupling with a continuum of scattering states. The protection from decay occurs whenever the relative phase in the overlap of bound and scattering state becomes a multiple of $\pi$. Experiments with spin-orbit excited noble gas dimers have confirmed our theoretical prediction of phase protection. The probability of phase protection increases with reduced mass, well depth and equilibrium distance of the potential supporting the quasi-bound state, providing a blueprint to identify quantum states that are intrinsically protected against undesired decay.

4 Photoelectron Circular Dichroism and Its Coherent Control

The third example showcases a quantum effect that is observed in experiments with molecular beams when circularly polarized light ionizes molecules which are chiral [7]. Remarkably, when a molecule is chiral, i.e., when its nuclear scaffold exhibits a handedness, ionization of randomly oriented molecules with right circularly polarized light does not yield the same photoelectron angular distribution as that with left circularly polarized light [26]. The difference between the photoelectron angular distributions obtained with left and right circularly polarized light is called photoelectron circular dichroism (PECD). Instead of exchanging the polarization direction of the light, one can also exchange the handedness of the molecule to observe PECD [26]. Unlike other dichroic effects, PECD does not involve a magnetic dipole moment and is obtained merely within the electric dipole approximation of the light-matter interaction [26].

First order perturbation theory for the photoionization cross section reveals the mechanism underlying the dichroic effect [26]: For a chiral molecule, the photoionization matrix elements with opposite spatial orientation do not cancel when averaging over the Euler angles. This gives rise to terms in the cross section that are odd under inversion of the polar angle and thus to dichroism. More intuitively, the photoionization cross section involves two rotations—of the polarization axis into the molecular frame and of the photoelectron momentum into the lab frame—which are sufficient to be sensitive to the handedness of the molecular scaffold. This geometric picture can be made more rigorous by noticing that the angle-resolved photoionization cross section is a vector observable which can be expressed as a triple product [27]. For non-coplanar vectors forming the triple product, the observable becomes enantiosensitive [27].

While theoretically predicted in the mid-1970s [26] and first observed with synchrotron radiation in the early 2000s [28], femtosecond laser pulses driving multi-photon ionization have made PECD accessible in table-top experiments [7, 29,30,31,32]. Since multi-photon ionization probes intermediate electronically excited states [7, 33], a theoretical description beyond first order in the perturbation theory for the light-matter interaction is called for. At the same time, the bicyclic ketones with which the experiments have been carried out, for example, fenchone, camphor, or limonene, are amenable to a high-level treatment of their electronically excited states. In contrast, modeling the photoionization continuum from first principles is rather challenging.

A way to address this challenge, applied to the specific example of resonantly enhanced (2+1) multi-photon ionization (REMPI) of fenchone and camphor [5], separates the non-resonant two-photon excitation from the one-photon ionization. The former can be described with coupled cluster theory whereas for the latter a single active electron approach using hydrogenic orbitals captures the essential physics of the photoelectron moving in a Coulombic potential [5]. Neglecting any coherent effects during the excitation, the ionization probes an anisotropic distribution of electronically excited molecules. This is due to the anisotropy of the two-photon absorption tensors of the molecules [5]. The properties of the two-photon absorption alone are, however, not sufficient to determine which intermediate state is probed by the REMPI process. Based on energetic arguments, there are five possible candidate states, only one of which is ruled out when using the information of the two-photon absorption tensors in the calculation of the photoionization cross section [5]. When including also the properties of the probed electronically excited states, only one out of the five candidates is in agreement with the experimental data [5]. Interestingly, the theoretically predicted intermediate state differs for fenchone compared to camphor [5]. This might explain the different photoelectron angular distributions and different PECD observed for these two chemically very similar molecules [7].

There are many intriguing questions that arise in the context of PECD, for example whether the effect is determined by the initial, the final, or the intermediate state of the process. In order to answer such questions, a more rigorous description of PECD and related effects in the ionization of chiral molecules is required. In particular, a better description of the photoionization continuum including electron correlation effects and the ability to treat coupled electronic and vibrational motion are called for. At the same time, PECD provides a very convenient experimental handle to probe the chiroptical response of molecules, and it is natural to ask whether this response can be enhanced by suitably shaping the ionizing field, in the spirit of coherent control of photoinduced dynamics [34, 35].

This question can be answered by combining the time-dependent configuration interaction singles (CIS) method for the electronic structure [36], second order perturbation theory for the light-matter interaction, and parameter optimization for the electric field using sequential parametrization updates [37]. Figure 4 illustrates the ionization pathways that are accounted for in this description. Pathways ending at the same final kinetic energy of the photoelectron (within the spectral bandwidth of the pulse) can interfere with each other, cf. the red and green arrows in Fig. 4. This can be thought of as a spectral realization of a double-slit experiment, with the additional advantage that the relative phase between the two pathways can be adjusted by properly tuning the ionizing electric field in its amplitude and phase [35].

Fig. 4

One-photon and two-photon ionization pathways within the time-dependent CIS framework

Fig. 5

Adapted from Ref. [6]

PECD after ionization of CHBrClF with a bichromatic guess pulse with flat spectral phase (left), optimized bichromatic (center) and freely optimized (right) electric fields. The percentage is taken with respect to the isotropic yield, and the increase is due to interference between one-photon and two-photon pathways (center), respectively between different two-photon pathways probing different intermediate states (right).

A bichromatic pulse driving the red and green ionization pathways in Fig. 4 is thus a natural starting point for optimizing the electric field. When ionizing a chiral methan derivate with such a pulse, assuming a flat spectral phase, a PECD of about 4% (relative to the isotropic ionization yield) is obtained [6]. When optimizing the field, constraining the pulse to be bichromatic, the PECD is pushed up to about 20%. This is shown in the center panel of Fig. 5. Compared to the initial guess pulse, the photon energies are lowered and, more importantly, the spectral phases of the two pulse components are adjusted to ensure that one-photon and two-photon ionization pathways interfere constructively. In contrast, with a flat spectral phase, the interference is mainly destructive. Indeed, constructive ionization of one-photon and two-photon pathway makes up for 17% out of the calculated 20% of PECD [6].

Fig. 6

Adapted from Ref. [6]

The freely optimized field drives various two-photon ionization pathways that, depending on the linear chirp of the low-frequency component of the ionizing field, respectively the time-delay between low-frequency and high-frequency pulse compontents, interfere constructively or destructively.

An even larger increase in PECD, up to almost 70%, is obtained when freely optimizing the ionizing electric field [6], cf. right panel of Fig. 5. This increase is driven by interference between various two-photon ionization pathways probing different intermediate, electronically excited states, illustrated in Fig. 6 (right). The optimized field turns out to have two spectral components, with the lower one exhibiting a linear spectral phase [6]. Such a “chirp” provides a very convenient handle to analyze the interference pattern in more detail, since changing the chirp rate, i.e., the slope of the spectral phase, amounts to changing the relative time delay between the low-frequency and the high-frequency component of the optimized pulse. If the low-frequency component precedes the high-frequency one, the PECD does not depend on the specific time delay and amounts to about 10%, cf. red-shaded parts in Fig. 6. If, in contrast, the high-frequency component arrives first, an electronic wavepacket is created which is then ionized by the low-frequency component of the pulse, cf. blue-shaded parts in Fig. 6. In this case, PECD sensitively depends on the time-delay, reflecting the time evolution of the electronic wave packet, oscillating between 6% and 62%. The largest PECD is obtained when the two spectral components of the optimized pulse overlap in time [6]. This allows for maximum interference between all the two-photon ionization pathways, highlighted by the yellow-shaded parts in Fig. 6.

In summary, photoelectron circular dichroism is a sensitive chiroptical probe of electron dynamics in a chiral potential, measured in experiments with molecular beams. Time-independent perturbation theory of resonantly enhanced (2+1) photoionization of camphor and fenchone molecules, combined with an ab initio description of the bound electronic spectrum based on coupled cluster theory, yields semi-quantitative agreement with the experimental data [5]. It emphasizes the role of orientation-selective excitation in multi-photon ionization and allows to identify the intermediate state that is probed by the REMPI process [5]. The magnitude of the chiroptical response can be enhanced by suitably shaping the ionizing field [6]. Time-dependent perturbation theory allows for directly identifying the quantum pathway interference responsible for the enhancement [6]. Whether there exists an upper bound for a chiroptical response such as photoelectron circular dichroism is one of the many open questions in the quantum control of molecular chirality.

5 Conclusions

This chapter reviewed three examples of quantum effects beyond entanglement — the (dis)appearance of a tunneling resonance in cold collisions, the protection of predissociation resonances by a phase, and the circular dichroism observed in the photoelectron spectrum of chiral molecules. In each case, a theoretical description based on first principles was key to elucidating the rather surprising observations made in experiments with molecular beams. The examples thus testify to the intriguing nature of quantum mechanics as well as to the topicality of Otto Stern’s legacy.