Skip to main content
SpringerLink
Log in

Study of the Anisotropy Effect in Piecewise Homogeneous Media by Boundary and Near-Boundary Element Methods

  • Conference paper
  • First Online:
Advances in Intelligent Systems and Computing V (CSIT 2020)

Part of the book series: Advances in Intelligent Systems and Computing ((AISC,volume 1293))

Included in the following conference series:

  • 403 Accesses

Abstract

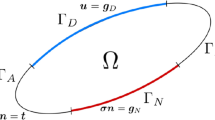
In this paper presents mathematical models for 2D and 3D problems of potential theory with consideration of anisotropy of the piecewise homogeneous medium. To find solutions of the respective problems of potential theory, indirect methods of boundary and near-boundary elements have been used. The orthotropy effect in homogeneous and piecewise-homogeneous half-spaces has been investigated. The effect of orthotropy in a medium without inclusions and with one inclusion is investigated. A software implementation of the proposed approach has been carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Pervago, E.V.: Influence of anisotropy and inhomogeneity on results of electrical sounding. Research Paper PhD Phys. & Math. sc., 83 p. MSU, Moscow (1998). (in Russian)

    Google Scholar 

  2. Bolshakov, D.K., Modin, I.N., Pervago, E.V., Shevnin, V.A.: New step in anisotropy studies: arrow-type array. In: Proceedings of 4th EEGS-ES Meeting in Barcelona, Spain (September 1998)

    Google Scholar 

  3. Yalov, T.V.: Numerical modeling of resistivity anisotropy fractured media. Geophysics, №. 3. Moscow State University (2016). (in Russian)

    Google Scholar 

  4. Watson, K.A., Barker, R.D.: Tank modeling of azimuthal resistivity surveys over anisotropic bedrock with dipping overburden. Near Surf. Geophys. 8, 297–309 (2010)

    Article  Google Scholar 

  5. Watson, K.A., Barker, R.D.: Modeling azimuthal resistivity sounding over a laterally changing resistivity subsurface. Near Surf. Geophys. 3(1), 3–11 (2005)

    Article  Google Scholar 

  6. Wishart, D.N., Staler, L.D.: Fracture anisotropy characterization in crystalline bedrock using field-scale azimuthal self potential gradient. J. Hydrol. 358, 35–45 (2008)

    Article  Google Scholar 

  7. Wishart, D.N., Slater, L.D., Schnell, D.L., Herman, G.C.: Hydraulic anisotropy characterization of pneumatic-fractured sediments using azimuthal self potential gradient. J. Contam. Hydrol. 103, 134–144 (2009)

    Article  Google Scholar 

  8. Aissaoui, R., Bounif, A., Zeyen, H., Messaoudi, S.-A.: Evaluation of resistivity anisotropy parameters in the Eastern Mitidja basin, Algeria, using azimuthal electrical resistivity tomography. Near Surf. Geophy. 17(4), 359–378 (2019)

    Google Scholar 

  9. Taylor, R.W., Fleming, A.H.: Characterizing jointed systems by azimuthal resistivity surveys. Ground Water 26(4), 464–474 (1998)

    Article  Google Scholar 

  10. Bahr, K.: Electrical anisotropy and conductivity distribution functions of fractal random networks and of the crust: the scale effect of connectivity. Geophys. J. Int. 130(3), 649–660 (1997)

    Article  Google Scholar 

  11. Bahr, K., Bantin, M., Jantos, Chr., Schneider, E., Storz, W.: Electrical anisotropy from electromagnetic array data: implications for the conduction mechanism and for distortion at long periods. Phys. Earth Planet. Inter. 119, 237–257 (2000)

    Article  Google Scholar 

  12. Gatzemeier, A., Moorkamp, M.: 3D modelling of electrical anisotropy from electromagnetic array data: hypothesis testing for different upper mantle conduction mechanisms. Phys. Earth Planet. Inter. 149, 225–242 (2005)

    Article  Google Scholar 

  13. Cembrowski, M., Junge, A.: Electrical anisotropy in the presence of oceans—a sensitivity study. Geophys. J. Int. 213(2), 1029–1043 (2018)

    Article  Google Scholar 

  14. Tongcheng, H., Denghui, X., Li-Yun, F., Fulai, L.: The role of spheroidal inclusions on the electrical anisotropy of transversely isotropic rocks. Geophys. J. Int. 218(1), 508–518 (2019)

    Article  Google Scholar 

  15. Loke, M.H., Dahlin, T.: A comparison of Gauss-Newton and quasi-Newton methods in resistivity imaging inversion. J. Appl. Geophys. 49(2002), 149–162 (2002)

    Article  Google Scholar 

  16. Brebbia, C.A., Telles, J.C.F., Wrobel, L.C.: Boundary element methods. Theory and Application in Engineering. Springer (1984)

    Google Scholar 

  17. Sauter, S.A., Schwab, C.: Boundary Element Methods. Springer, Heidelberg (2010)

    Book  Google Scholar 

  18. Zhuravchak, L.M., Grytsko, Ye.G.: The near-boundary element method in applied problem of mathematical physics. Carpathian Branch of S.I. Subbotin Institute of Geophysics, NAS of Ukraine, L’viv (1996). (in Ukrainian)

    Google Scholar 

  19. Zhuravchak, L.: Mathematical modelling of non-stationary processes in the piecewise-homogeneous domains by near-boundary element method. In: Shakhovska, N., Medykovskyy, M.O. (eds.) Springer Nature Switzerland AG 2020, CCSIT 2019, AISC 1080, pp. 64–77 (2020)

    Google Scholar 

  20. Mukanova, B., Modin, I.: The Boundary Element Method in Geophysical Survey. Springer, Cham (2018)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lviv Polytechnic National University, Lviv, Ukraine

    Liubov Zhuravchak

  2. Carpathian Branch of S.I. Subbotin Institute of Geophysics, National Academy of Sciences, Lviv, Ukraine

    Nataliya Zabrodska

Authors
  1. Liubov Zhuravchak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nataliya Zabrodska
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liubov Zhuravchak .

Editor information

Editors and Affiliations

  1. Department of Artificial Intelligence, Lviv Polytechnic National University, Lviv, Ukraine

    Natalya Shakhovska

  2. Institute of Computer Science and Information Technologies, Lviv Polytechnic National University, Lviv, Ukraine

    Mykola O. Medykovskyy

Rights and permissions

Reprints and permissions

Copyright information

© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Zhuravchak, L., Zabrodska, N. (2021). Study of the Anisotropy Effect in Piecewise Homogeneous Media by Boundary and Near-Boundary Element Methods. In: Shakhovska, N., Medykovskyy, M.O. (eds) Advances in Intelligent Systems and Computing V. CSIT 2020. Advances in Intelligent Systems and Computing, vol 1293. Springer, Cham. https://doi.org/10.1007/978-3-030-63270-0_37

Download citation

Publish with us

Policies and ethics

Search

Navigation