Abstract
We show that the loop O(n) model on the hexagonal lattice exhibits exponential decay of loop sizes whenever n > 1 and \(x<\tfrac {1}{\sqrt {3}}+\varepsilon (n)\), for some suitable choice of ε(n) > 0.
It is expected that, for n ≤ 2, the model exhibits a phase transition in terms of x, that separates regimes of polynomial and exponential decay of loop sizes. In this paradigm, our result implies that the phase transition for n ∈ (1, 2] occurs at some critical parameter x c(n) strictly greater than that \(x_c(1) = 1/\sqrt {3}\). The value of the latter is known since the loop O(1) model on the hexagonal lattice represents the contours of the spin-clusters of the Ising model on the triangular lattice.
The proof is based on developing n as 1 + (n − 1) and exploiting the fact that, when \(x<\tfrac {1}{\sqrt {3}}\), the Ising model exhibits exponential decay on any (possibly non simply-connected) domain. The latter follows from the positive association of the FK-Ising representation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This domination is of special interest as
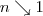 and for \(x \geq 1/\sqrt {3}\). Then we may simplify the value of β as \(\beta = \frac {(2+2\sqrt {3})^6}{ (n-1)^{2} + (2+2\sqrt {3})^6} \sim 1 - \tfrac 1{(2+2\sqrt {3})^{6}} (n-1)^{2}~\).
and for \(x \geq 1/\sqrt {3}\). Then we may simplify the value of β as \(\beta = \frac {(2+2\sqrt {3})^6}{ (n-1)^{2} + (2+2\sqrt {3})^6} \sim 1 - \tfrac 1{(2+2\sqrt {3})^{6}} (n-1)^{2}~\). - 2.
As
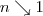 and \(x \geq 1/\sqrt {3}\), we may assume that \(\alpha \sim 1 - \tfrac {1}{6\, (2+2\sqrt {3})^{6}} (n-1)^{2}\).
and \(x \geq 1/\sqrt {3}\), we may assume that \(\alpha \sim 1 - \tfrac {1}{6\, (2+2\sqrt {3})^{6}} (n-1)^{2}\).
References
Aizenman, M., Barsky, D.J., Fernández, R.: The phase transition in a general class of Ising-type models is sharp. J. Statist. Phys. 47(3–4), 343–374 (1987)
Beffara, V., Duminil-Copin, H.: The self-dual point of the two-dimensional random-cluster model is critical for q ≥ 1. Probab. Theory Related Fields 153(3–4), 511–542 (2012)
Benoist, S., Hongler, C.: The scaling limit of critical Ising interfaces is CLE3. Ann. Probab. 47(4), 2049–2086 (2019)
Blöte, H.W., Nienhuis, B.: The phase diagram of the O(n) model. Phys. A Stat. Mech. Appl. 160(2), 121–134 (1989)
Camia, F., Newman, C.M.: Two-dimensional critical percolation: the full scaling limit. Commun. Math. Phys. 268(1), 1–38 (2006)
Chayes, L., Machta, J.: Graphical representations and cluster algorithms II. Phys. A Stat. Mech. Appl. 254(3), 477–516 (1998)
Chayes, L., Pryadko, L.P., Shtengel, K.: Intersecting loop models on \(\mathbb Z^d\): rigorous results. Nucl. Phys. B 570(3), 590–614 (2000)
Chelkak, D., Smirnov, S.: Universality in the 2D Ising model and conformal invariance of fermionic observables. Invent. Math. 189(3), 515–580 (2012)
Crawford, N., Glazman, A., Harel, M., Peled, R.: Macroscopic loops in the loop O(n) model via the XOR trick. Preprint arXiv: 2001.11977 (2020)
Domany, E., Mukamel, D., Nienhuis, B., Schwimmer, A.: Duality relations and equivalences for models with O(n) and cubic symmetry. Nucl. Phys. B 190(2), 279–287 (1981)
Duminil-Copin, H., Smirnov, S.: The connective constant of the honeycomb lattice equals \(\sqrt {2+\sqrt {2}}\). Ann. Math. (2) 175(3), 1653–1665 (2012)
Duminil-Copin, H., Glazman, A., Peled, R., Spinka, Y.: Macroscopic loops in the loop O(n) model at Nienhuis’ critical point. Preprint arXiv:1707.09335 (2017)
Duminil-Copin, H., Peled, R., Samotij, W., Spinka, Y.: Exponential decay of loop lengths in the loop O(n) model with large n. Commun. Math. Phys. 349(3), 777–817, 12 (2017)
Friedli, S., Velenik, Y.: Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction. Cambridge University, Cambridge (2017)
Glazman, A., Manolescu, I.: Uniform Lipschitz Functions on the Triangular Lattice have Logarithmic Variations. Preprint arXiv:1810.05592 (2018)
Grimmett, G.: The random-cluster model. In: Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 333. Springer, Berlin (2006)
Holley, R.: Remarks on the FKG inequalities. Comm. Math. Phys. 36, 227–231 (1974)
Kager, W., Nienhuis, B.: A guide to stochastic Löwner evolution and its applications. J. Statist. Phys. 115(5–6), 1149–1229 (2004)
Lenz, W.: Beitrag zum Verständnis der magnetischen Eigenschaften in festen Körpern. Phys. Zeitschr. 21, 613–615 (1920)
Nienhuis, B.: Exact critical point and critical exponents of O(n) models in two dimensions. Phys. Rev. Lett. 49(15), 1062–1065 (1982)
Onsager, L.: Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. (2) 65, 117–149 (1944)
Peled, R., Spinka, Y.: Lectures on the spin and loop O(n) models. In: Sojourns in Probability Theory and Statistical Physics-I, pp. 246–320 (2019)
Smirnov, S.: Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris Sér. I Math. 333(3), 239–244 (2001)
Smirnov, S.: Conformal invariance in random cluster models. I. Holomorphic fermions in the Ising model. Ann. Math. (2) 172(2), 1435–1467 (2010)
Taggi, L.: Shifted critical threshold in the loop O(n) model at arbitrary small n. Electron. Commun. Probab. 23(96), 9 (2018)
Acknowledgements
The authors would like to thank Ron Peled for suggesting to develop in n = (n − 1) + 1 following Chayes and Machta. Our discussions with Hugo Duminil-Copin, Yinon Spinka and Marcelo Hilario were also very helpful. We acknowledge the hospitality of IMPA (Rio de Janeiro), where this project started.
The first author is supported by the Swiss NSF grant P300P2_177848, and partially supported by the European Research Council starting grant 678520 (LocalOrder). The second author is a member of the NCCR SwissMAP.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Glazman, A., Manolescu, I. (2021). Exponential Decay in the Loop O(n) Model on the Hexagonal Lattice for n > 1 and \(x<\tfrac {1}{\sqrt {3}}+\varepsilon (n)\) . In: Vares, M.E., Fernández, R., Fontes, L.R., Newman, C.M. (eds) In and Out of Equilibrium 3: Celebrating Vladas Sidoravicius. Progress in Probability, vol 77. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-60754-8_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-60754-8_21
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-60753-1
Online ISBN: 978-3-030-60754-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


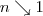 and for
and for 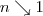 and
and