Keywords

1 Introduction

Johnson, Kendall and Roberts published 1971 their famous work on adhesive contact of elastic parabolic bodies [1]. Contrary to the non-adhesive contact, an adhesive contact shows a hysteresis: the dependencies of force on approach depend on whether the bodies are brought into contact or pulled off. The area enclosed in the hysteresis loop is the energy, which is irreversible dissipated during one complete “cycle” of an adhesive contact. According to the JKR theory, after the first contact, an adhesive neck of finite radius appears. If we now would try to pull off the bodies, they remain in contact even for negative values of the indentation depth up to the point of instability where the contact is lost at once. The mechanical energy is irreversibly lost only in such points of instabilities [2]. Both before and after the instability, the processes of approach and detachment are reversible, which is obvious if we remember that the JKR theory is based on the principle of virtual work, which assumes absence of static frictional forces [3]. However, experiments show that adhesive contacts show often pronounced hysteresis even after the formation of initial contact [4,5,6]. Some authors attribute this to plastic deformation [5]. However, it was shown in [6, 7] that such hysteresis could be seen also in pure elastic contacts between rough bodies. The mechanism of this hysteresis is very simple: The energy dissipation occurs in each act of instable movement of the contact boundary. If the contact area has a complicated shape, the movement of the boundary can proceed in a series of jumps [8] leading to energy dissipation, which means that the boundary feels a dissipative force (see also the supplementary video [9]). Another mechanism of the adhesive hysteresis in the already formed contact state could be the chemical heterogeneity of the contact interface. In the present paper, we analyze this mechanics on a simple example when both the shape of contacting bodies and the chemical heterogeneity have axial symmetry.

2 Problem Statement and Model Description

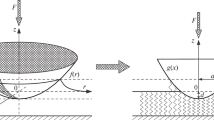
Consider an adhesive contact between an axissymmetrical rigid body \( z = f(r) , \) where \( z \) is the coordinate in the normal to interface direction and \( r \) polar radius in the contact plane, and an elastic half space. It is assumed that the specific work of adhesion assumes two constant values \( \gamma_{1} \) and \( \gamma_{2} \) in the alternating rings having the widths \( h_{1} \) and \( h_{2} \) (Fig. 1). In the framework of the Method of Dimensionality Reduction (MDR) [10, 11], it is possible to map a three-dimensional axisymmetric contact problem to a contact of the modified plane shape

Fig. 1
figure 1

Schematic representation of the chemical heterogeneity in the considered system. The specific work of adhesion take two constant values \( \gamma_{1} \) and \( \gamma_{2} \) in the alternating rings having the widths \( h_{1} \) and \( h_{2} \)

Full size image
$$ g(x) = \left| x \right|\int\limits_{0}^{\left| x \right|} {\frac{{f^{\prime}(r)}}{{\sqrt {x^{2} - r^{2} } }}{\text{d}}r} \,. $$
(1)

and a one-dimensional elastic foundations consisting of independent springs (Fig. 2) having the stiffness

Fig. 2
figure 2

Scheme of the MDR-representation of an adhesive contact. The equivalent profile \( g(x) \) given by (1) is brought into contact with elastic foundation defined by Eq. (2). The contact radius is defined by the condition that the elongation of the springs at the boundary of the contact is given by the rule of Heß, Eq. (5). The normal force, contact radius and the indentation depth in this MDR-model are the same as in the initial three-dimensional contact problem

Full size image
$$ \Delta k = E^{*} \Delta x. $$
(2)

Here \( \Delta x \) is the space between two adjacent springs, and

$$ E^{*} = E/(1 - \nu^{2} ), $$
(3)

with \( E \) the Young modulus and \( \nu \) the Poisson number of the elastic half-space.

In the MDR, it can be shown [10, 11] that the indentation depth, the contact radius and the normal force calculated as a sum of forces of all springs in contact:

$$ F\left( a \right) = 2E^{*} \int\limits_{0}^{a} {\left( {d - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}\,} $$
(4)

coincide with their values in the original three-dimensional problem. The radius of the adhesive contact is determined from the requirement of the minimum of the total energy of the system. This means that if detachment of two springs on both sides of the contact is leading to a decrease of the total energy (elastic energy plus surface energy) then it will detach. On the other hand, if the formation of contact for the springs adjacent to those at the edge of the contact, leads to a decrease of energy, the contact will spread further. Detachment of two springs leads to a decrease of elastic energy by \( E^{*} \cdot \Delta x \cdot \Delta l^{2} \), where \( \Delta l \) is the elongation which a spring has in the attached state (Fig. 2). When it detaches, a free surface having the area \( 2\pi a\Delta x \) is formed, which increases the energy by the work of separation \( 2\pi a\Delta x\gamma \). The boundary is in equilibrium if these two energies are equal and thus

$$ \Delta l = \sqrt {\frac{2\pi a\gamma }{{E^{*} }}} . $$
(5)

This equation, which is equivalent to the Griffith criterion for crack equilibrium [12], was first found first found by Heß [13] and is known as rule of Heß [14]. Using the relation \( u(x) = d - g(x) \), where \( u(x) \) is the vertical displacement at the position \( x \), we can rewrite (5) in the form

$$ d = g(a) - \sqrt {\frac{2\pi a\gamma }{{E^{*} }}} . $$
(6)

This equation connects the indentation depth with the equilibrium contact radius, \( a \). In the following, for simplicity, we will assume that the contact is realized by a very stiff system, which means that the indentation \( d \) can be considered as controlling parameter.

3 Attachment and Detachment of a Chemically Heterogeneous Body

Consider the system with specific surface energy depending on the position as shown in Fig. 1. Assume \( \gamma_{1} < \gamma_{2} \). During the indentation, there are three repeating stages in the movement (Fig. 3).

Fig. 3
figure 3

Processes of approach, formation of contact and pull-off for a heterogeneous contact. During the Stage (1), the boundary moves reversibly along the ring with lower specific surface energy. During the Stage (2) it jumps over the ring with higher specific surface energy. During the Stage (3) it “sticks” in this position until the force reaches the JKR curve. This movement occurs at a constant contact radius and is thus linear. After that, this quasi-periodic process is repeated (the repetitions are not shown in the Figure). If the direction of movement is changed to the opposite (“turning point”), the contact radius first remains constant causing a linear dependency of the normal force on approach. After the force have reached the JKR curve corresponding to the higher specific surface energy, the process consisting of reversible propagation inside the rings with high specific surface energy, jumps over the rings with low specific surface energy and linear returns to the JKR curve

Full size image

(1) If at some moment of time the contact radius \( a_{1} \) coincides with the inner edge of the ring having the surface energy \( \gamma_{1} \), then at this moment

$$ d_{1} = g(a_{1} ) - \sqrt {\frac{{2\pi a_{1} \gamma_{1} }}{{E^{*} }}} . $$
(7)

If the indentation depth increases, the contact radius will also increase (exactly accordingly to the corresponding JKR curve with surface energy \( \gamma_{1} \), Fig. 3, Stage (1)) unless it reaches the outer edge of the ring having the surface energy \( \gamma_{1} \). At this moment

$$ d_{2} = g(a_{2} ) - \sqrt {\frac{{2\pi a_{2} \gamma_{1} }}{{E^{*} }}} , \, a_{2} = a_{1} + h_{1} . $$
(8)

(2) Further increasing of indentation depth leads to a jump-like increase of the surface energy. Therefore, the contact boundary will jump over the whole width of the ring with higher surface energy (at the given indentation depth (8)) and stop at the edge of the ring having lower surface energy. At this point, the configuration is given by the pair

$$ (d_{2} , \, a_{2} + h_{2} ). $$
(9)

This jump in the contact area will lead to a (negative) jump in the force (see Fig. 3, Stage (2)).

(3) During further indentation, the contact radius will remain constant and the force will therefore increase linearly with indentation depth until it reaches again the JKR curve.

After that, we are again in the repetition of the Stage (1), and the movement occurs along the JKR curve to the next jump, and so on.

We see that in the phase of indentation the system follows the JKR curve corresponding to the lower surface energy, with periodic negative jumps and linear returns to the JKR curve. The maximum amplitude of a jump corresponds to the “distance” between the JKR curves for \( \gamma_{1} \) and \( \gamma_{2} \). In the following, we assume that the amplitude of jumps is small compared to this “distance”. Under this assumption, the indentation occurs practically along the JKR curve for smaller surface energy with small variations.

If at some point the indentation stops and reversed movement starts, then the system first remains stuck in this point. This is because in spreading, the contact area is pinned by the areas with lower specific surface energy while in detaching, it is pinned by the areas with higher specific surface energy. Therefore, the transition from indentation to pulling off first leads to the “switching of the criterion for propagation” which leads to pinning the boundary to the position at the beginning of reverse motion. As the contact area remains constant, the force-distance dependency is in this stage linear until the force reaches the JKR curve corresponding to the higher specific surface energy. In the following, it moves along the JKR curve corresponding to the higher specific surface energy until the boundary reaches the ring with lower energy. At this point, the whole ring with low surface energy detaches at once causing a (positive) jump in the normal fore. After that, the contact area remains constant and the normal force depends linearly on the indentation depth until this linear dependency reaches the JKR-curve (Fig. 3). Thus, the back movement is very similar to the indentation with the only difference that now the systems moves along the JKR curve corresponding to the higher specific surface energy. The hysteresis and the corresponding energy dissipation is solely due to instable stages (jumps). This mechanism of energy dissipation is very similar to that described by Prandtl [15, 16].

4 Complete Cycle of Attachment and Detachment

The attachment-detachment process becomes especially simple if we assume that the thickness of the rings with different values of specific surface energy are so small that they are not “seen” from the macroscopic point of view. It is easy to give mathematical form to this condition.

In the state (8), the normal force is given by

$$ F_{2} = 2E^{*} \int\limits_{0}^{{a_{1} + h_{1} }} {\left( {d_{2} - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}\,} $$
(10)

and in the state (9) by

$$ F_{3} = 2E^{*} \int\limits_{0}^{{a_{1} + h_{1} + h_{2} }} {\left( {d_{2} - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}} . $$
(11)

The jump of the force is estimated as

$$ \begin{aligned} F_{2} - F_{3} = 2E^{*} \left[ {\int\limits_{0}^{{a_{2} }} {\left( {d_{2} - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}\,} - \int\limits_{0}^{{a_{2} + h_{2} }} {\left( {d_{2} - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}\,} } \right] \hfill \\ = - 2E^{*} \left[ {\int\limits_{{a_{2} }}^{{a_{2} + h_{2} }} {\left( {d_{2} - g\left( {\tilde{a}} \right)} \right){\text{d}}\tilde{a}\,} } \right] \approx 2E^{*} h_{2} \Delta l(a_{2} ) = h_{2} \sqrt {8\pi E^{*} a_{2} \gamma_{1} } \;. \hfill \\ \end{aligned} $$
(12)

For a rough estimation let us introduce a “characteristic value” of the specific surface energy, \( \gamma \) (e.g. the average of \( \gamma_{1} \) and \( \gamma_{2} \)), the “characteristic value” of the ring width as \( h \) and the “characteristic value” of contact radius, \( a \), e.g. the critical value at the neck formation,

$$ a = \left( {\frac{{9\pi R^{2} \gamma }}{{8E^{*} }}} \right)^{1/3} . $$
(13)

Then the characteristic value of a jump in the force will be \( \Delta F_{\text{Jump}} \approx h\sqrt {8\pi E^{*} a\gamma } \) and that of the “distance” between the two JKR curves \( \Delta F_{0} \approx (3/2)\pi R\gamma \), [11]. The condition that the jumps are small compared with \( \Delta F_{0} \) can now be written as

$$ \frac{{\Delta F_{\text{Jump}} }}{{\Delta F_{0} }} \approx \frac{h}{R}\sqrt {\frac{{32E^{*} a}}{9\pi \gamma }} < < 1 $$
(14)

or

$$ h^{3} < < R^{2} \frac{\gamma }{{E^{*} }}. $$
(15)

This form is applicable only for indenters with parabolic shape. Written in the form

$$ h < < a, $$
(16)

it can be applied to any shapes. The criterion just means that the characteristic size of heterogeneity should be much smaller than the contact area.

If this condition is fulfilled, we will only see the averaged macroscopic behavior. As was shown in the Sect. 3, the contact configurations and the force-indentation dependencies will follow the JKR solution corresponding to the lower surface energy, \( \gamma_{1} \). On the return, the system follows the JKR curve with higher surface energy, \( \gamma_{2} \). The transition from one curve to the other at the turning point occurs via a linear force-displacement dependency at a constant contact radius (Fig. 4).

Fig. 4
figure 4

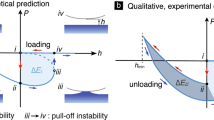
A complete cycle of the force-indentation dependence for indentation and detachment for the case that the thickness of rings is “microscopic” so that the jumps are not seen on the macroscopic level. In this case, approach occurs along the JKR-curve corresponding to lower specific surface energy and pull-off along the JKR curve for higher surface energy. The are connected by a linear part following the turning point

Full size image

Adhesion cycles of the shape qualitatively very similar to that presented in Fig. 4 are often observed in experiment. As an example, in Fig. 5 results are shown, which have been obtained experimentally in the papers [17, 18]. Experiments were carried out by indenting a glass ball against a plane PDMS substrate and subsequent pulling it off. The main features of the behavior are the same as predicted theoretically: Both during loading and during unloading, the system moves along the JKR curves, however, corresponding to different specific surface energies. By turning, a transition from one curve to the other occurs.

Fig. 5
figure 5

Experimental loading-unloading curves (adapted from the paper [17]). According to [17], curves were measured using AFM for contacts between a glass sphere and a PDMS substrate. The glass sphere was of diameter ≈ 50 μm. The gray dashed curves are the fit of the loading and unloading branches of the measured P–h data to the JKR theory. Comparison with theoretical curves in Fig. 4 shows that the contact behavior in experiment is, at least qualitatively very similar to that predicted theoretically: In the loading phase the system moves along a JKR curve corresponding to a lower specific energy. During unloading the transition from one JKR curve to the other one can be clearly identified

Full size image

Another example of loading-unloading curves showing very clearly the linear transition region after turning from loading to unloading is shown in Fig. 6. The contact area was observed and recorded by a video camera placed beneath the rubber sheet. In the videos (which are not part of this publication), it is clearly seen that after changing the direction of loading the contact area first remained unchanged. During this “sticking phase”, the dependency of the normal force on approach follows a linear dependency, which can be easily identified in Fig. 6.

Fig. 6
figure 6

a Loading-unloading curve for an adhesive contact between a spherical steel indenter (radius of curvature R = 33 mm) and a layer of soft transparent rubber TARNAC CRG N3005 (thickness 5 mm). Part of experimental setup is shown in subplot (b). In the subplot (a), it is clearly seen that after changing the direction of motion, a long linear part of the force-distance dependency is observed. Observation of the contact area via a video camera from beneath the layer shows that during the linear part of this curve the contact area remains constant

Full size image

5 Conclusions

We considered a simple adhesive contact with axially symmetric chemical heterogeneity of the interface. In this case, the system follows the JKR curves both during the indentation and detachment phases. However, there exist two different specific surface energies – one for forming the contact (during indentation) and the other one for its destruction (pull off). During the indentation, the system follows the JKR curve corresponding the lower specific surface energy, and during retraction the JKR curve corresponding to the higher value. If the chemical heterogeneity can be considered as “microscopic” (that means that the characteristic wavelength of heterogeneity fulfils the criterion (15) or (16)) this result does not depend on the absolute and relative thicknesses of the regions with different specific surface energies, but depends solely on the values of surface energy itself.

The main conclusions of this paper seem to be very generic. The predicted features are often observed in experimental systems not fulfilling the simple assumptions of the present model. The reason for such generality maybe just that the chemical heterogeneity leads to appearance of a force of friction for the moving contact boundary. From the macroscopic, phenomenological point of view, it is not important what is the physical mechanism leading to microscopic instabilities and thus friction in the boarder line. This can be regular heterogeneity as in the present paper or irregular heterogeneity (which also leads to local instabilities in movement of the contact boundary) or roughness. Macroscopically, the appearance of the force of friction of boundary line is equivalent to existence of two surface energies—for closing and for opening the contact. Thus, the phenomenological appearance may be the same independently of particular mechanism leading to the boundary line friction.

It would be interesting to prove whether this main conclusion will remain valid for non-axially symmetric cases and what are then the governing parameters determining the effective surface energies.