Abstract
A Sturmian sequence is an infinite nonperiodic string over two letters with minimal subword complexity. In two papers, the first written by Morse and Hedlund in 1940 and the second by Coven and Hedlund in 1973, a surprising correspondence was established between Sturmian sequences on one side and rotations by an irrational number on the unit circle on the other. In 1991 Arnoux and Rauzy observed that an induction process (invented by Rauzy in the late 1970s), related with the classical continued fraction algorithm, can be used to give a very elegant proof of this correspondence. This process, known as the Rauzy induction, extends naturally to interval exchange transformations (this is the setting in which it was first formalized). It has been conjectured since the early 1990s that these correspondences carry over to rotations on higher dimensional tori, generalized continued fraction algorithms, and so-called S-adic sequences generated by substitutions. The idea of working towards such a generalization is known as Rauzy’s program. Recently Berthé, Steiner, and Thuswaldner made some progress on Rauzy’s program and were indeed able to set up the conjectured generalization of the above correspondences. Using a generalization of Rauzy’s induction process in which generalized continued fraction algorithms show up, they proved that under certain natural conditions an S-adic sequence gives rise to a dynamical system which is measurably conjugate to a rotation on a higher dimensional torus. Moreover, they established a metric theory which shows that counterexamples like the one constructed in 2000 by Cassaigne, Ferenczi, and Zamboni are rare. It is the aim of the present chapter to survey all these ideas and results.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This implies that u and v have Σx and Σy in their orbit where x and y are the two limit sequences of σ. This interesting fact, which is not needed in this proof, should be proved by the reader.
- 2.
We could also have started with writing out 1 and going to the right from the origin. This would have produced the second limit sequence of (σ) which coincides with w save for the first two letters.
- 3.
A sequence is called linearly recurrent if there is a constant K such that each of its factors u occurs infinitely often in the sequence with gaps bounded by K|u|.
- 4.
A sequence is called uniformly recurrent if each of its factors occurs infinitely often in the sequence with bounded gaps.
- 5.
If we impose the additional property of primitivity on the coding sequence of a sequence \(w\in \mathcal {A}^{\mathbb {N}}\) it turns out that X w depends only on the directive sequence σ defining the S-adic sequence w and we have X σ = X w. This will be worked out precisely in Sect. 3.5.
- 6.
Only the first letter a n in the argument of σ [0,n) is relevant for the limit. However, since we use the topology on \(\mathcal {A}^{\mathbb {N}}\) and \(\sigma _{[0,n)}(a_{n})\not \in \mathcal {A}^{\mathbb {N}}\) we have to write σ [0,n)(a na n…).
- 7.
In [111] a space of tilings is equipped with a topology by saying that two tilings are close to each other if their tiles are close to each other in Hausdorff metric inside a large ball around the origin. Although \(\mathcal {C}_{\mathbf {v}}\) and \(\mathcal {C}^{(n_k)}_{\mathbf {v}}\) are no tilings, an analogous topology can be used here: \(\mathcal {C}_{\mathbf {v}}\) and
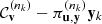 are said to be close to each other if Γ(v) and \(\varGamma ({\mathbf {v}}^{(n_k)})-{\mathbf {y}}_k\) coincide inside a large ball B around the origin and the tiles associated to an element of [y, i] ∈ Γ(v) ∩ B in each of these two collections are close to each other in Hausdorff metric.
are said to be close to each other if Γ(v) and \(\varGamma ({\mathbf {v}}^{(n_k)})-{\mathbf {y}}_k\) coincide inside a large ball B around the origin and the tiles associated to an element of [y, i] ∈ Γ(v) ∩ B in each of these two collections are close to each other in Hausdorff metric. - 8.
- 9.
Note that there are two kinds of shifts: the one just defined acts on the sequence of substitutions \(S^{\mathbb {N}}\), the other one (the S-adic shift) acts on the set of sequences X σ which is defined in terms of a single sequence of substitutions \({\boldsymbol {\sigma }}\in S^{\mathbb {N}}\). It should cause no confusion that both of these shift mappings are denoted by Σ.
- 10.
Not to be confused with the level n subtiles introduced in Sect. 3.7.1.
- 11.
Here ∥⋅∥2 is the operator norm w.r.t. the Euclidean norm on \(\mathbb {R}^d\).
References
B. Adamczewski, Balances for fixed points of primitive substitutions. Theor. Comput. Sci. 307(1), 47–75 (2003). Words
S. Akiyama, Self affine tilings and Pisot numeration systems, in Number Theory and Its Applications, ed. by K. Győry, S. Kanemitsu (Kluwer, Dordrecht, 1999), pp. 1–17
S. Akiyama, On the boundary of self affine tilings generated by Pisot numbers. J. Math. Soc. Japan 54(2), 283–308 (2002)
S. Akiyama, M. Barge, V. Berthé, J.Y. Lee, A. Siegel, On the Pisot substitution conjecture, in Mathematics of Aperiodic Order. Progr. Math., vol. 309 (Birkhäuser/Springer, Basel, 2015), pp. 33–72
S. Akiyama, T. Sadahiro, A self-similar tiling generated by the minimal Pisot number, in Proceedings of the 13th Czech and Slovak International Conference on Number Theory (Ostravice, 1997), vol. 6 (1998), pp. 9–26
J.P. Allouche, J. Shallit, Automatic Sequences: Theory, Applications, Generalizations. (Cambridge University Press, Cambridge, 2003)
A. Andres, R. Acharya, C. Sibata, Discrete analytical hyperplanes. Graph. Model. Image Process. 59, 302–309 (1997)
L. Arnold, Random Dynamical Systems. Springer Monographs in Mathematics (Springer, Berlin, 1998)
P. Arnoux, Un exemple de semi-conjugaison entre un échange d’intervalles et une translation sur le tore. Bull. Soc. Math. France 116(4), 489–500 (1989) (1988)
P. Arnoux, Le codage du flot géodésique sur la surface modulaire. Enseign. Math. (2) 40(1-2), 29–48 (1994)
P. Arnoux, Continued fractions: natural extensions and invariant measures, in Natural Extension of Arithmetic Algorithms and S-adic System. RIMS Kôkyûroku Bessatsu, vol. B58 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2016), pp. 19–32
P. Arnoux, V. Berthé, M. Minervino, W. Steiner, J. Thuswaldner, Nonstationary Markov partitions, flows on homogeneous spaces, and continued fractions (2018, in preparation)
P. Arnoux, S. Ferenczi, P. Hubert, Trajectories of rotations. Acta Arith. 87(3), 209–217 (1999)
P. Arnoux, A.M. Fisher, The scenery flow for geometric structures on the torus: the linear setting. Chinese Ann. Math. Ser. B 22(4), 427–470 (2001)
P. Arnoux, A.M. Fisher, Anosov families, renormalization and non-stationary subshifts. Ergodic Theory Dyn. Syst. 25(3), 661–709 (2005)
P. Arnoux, M. Furukado, E. Harriss, S. Ito, Algebraic numbers, free group automorphisms and substitutions on the plane. Trans. Am. Math. Soc. 363(9), 4651–4699 (2011)
P. Arnoux, E. Harriss, What is …a Rauzy fractal? Not. Am. Math. Soc. 61(7), 768–770 (2014)
P. Arnoux, S. Ito, Pisot substitutions and Rauzy fractals. Bull. Belg. Math. Soc. Simon Stevin 8(2), 181–207 (2001). Journées Montoises d’Informatique Théorique (Marne-la-Vallée, 2000)
P. Arnoux, S. Labbé, On some symmetric multidimensional continued fraction algorithms. Ergodic Theory Dyn. Syst. 38, 1601–1626 (2018)
P. Arnoux, M. Mizutani, T. Sellami, Random product of substitutions with the same incidence matrix. Theor. Comput. Sci. 543, 68–78 (2014)
P. Arnoux, A. Nogueira, Mesures de Gauss pour des algorithmes de fractions continues multidimensionnelles. Ann. Sci. École Norm. Sup. (4) 26(6), 645–664 (1993)
P. Arnoux, G. Rauzy, Représentation géométrique de suites de complexité 2n + 1. Bull. Soc. Math. France 119(2), 199–215 (1991)
P. Arnoux, T.A. Schmidt, Cross sections for geodesic flows and α-continued fractions. Nonlinearity 26(3), 711–726 (2013)
P. Arnoux, T.A. Schmidt, Commensurable continued fractions. Discrete Contin. Dyn. Syst. 34(11), 4389–4418 (2014)
P. Arnoux, Š. Starosta, The Rauzy gasket, in Further Developments in Fractals and Related Fields. Trends Mathematics (Birkhäuser/Springer, New York, 2013), pp. 1–23
E. Artin, Ein mechanisches System mit quasiergodischen Bahnen. Abh. Math. Sem. Univ. Hamburg 3(1), 170–175 (1924)
J. Auslander, Minimal Flows and Their Extensions. North-Holland Mathematics Studies, vol. 153. (North-Holland Publishing Co., Amsterdam, 1988). Notas de Matemática [Mathematical Notes], 122
A. Avila, V. Delecroix, Some monoids of Pisot matrices (2015). Preprint, http://arxiv.org/abs/1506.03692
A. Avila, P. Hubert, A. Skripchenko, Diffusion for chaotic plane sections of 3-periodic surfaces. Invent. Math. 206(1), 109–146 (2016)
A. Avila, P. Hubert, A. Skripchenko, On the Hausdorff dimension of the Rauzy gasket. Bull. Soc. Math. France 144(3), 539–568 (2016)
G. Barat, V. Berthé, P. Liardet, J. Thuswaldner, Dynamical directions in numeration. Ann. Inst. Fourier (Grenoble) 56(7), 1987–2092 (2006). Numération, pavages, substitutions
M. Barge, The Pisot conjecture for β-substitutions. Ergodic Theory Dyn. Syst. 38(2), 444–472 (2016)
M. Barge, Pure discrete spectrum for a class of one-dimensional substitution tiling systems. Discrete Contin. Dyn. Syst. 36(3), 1159–1173 (2016)
M. Barge, B. Diamond, Coincidence for substitutions of Pisot type. Bull. Soc. Math. France 130(4), 619–626 (2002)
M. Barge, J. Kellendonk, Proximality and pure point spectrum for tiling dynamical systems. Mich. Math. J. 62(4), 793–822 (2013)
M. Barge, J. Kwapisz, Geometric theory of unimodular Pisot substitutions. Amer. J. Math. 128(5), 1219–1282 (2006)
M. Barge, S. Štimac, R.F. Williams, Pure discrete spectrum in substitution tiling spaces. Discrete Contin. Dyn. Syst. 33(2), 579–597 (2013)
A.Y. Belov, G.V. Kondakov, I.V. Mitrofanov, Inverse problems of symbolic dynamics, in Algebraic Methods in Dynamical Systems. Banach Center Publ., vol. 94 (Polish Acad. Sci. Inst. Math., Warsaw, 2011), pp. 43–60
J. Bernoulli, Sur une nouvelle espece de calcul. Recueil pour les Astronomes, Berlin, vol. 1 (1772), pp. 255–284
J. Berstel, Transductions and context-free languages, Leitfäden der Angewandten Mathematik und Mechanik [Guides to Applied Mathematics and Mechanics], vol. 38 (B. G. Teubner, Stuttgart, 1979)
V. Berthé, Multidimensional Euclidean algorithms, numeration and substitutions. Integers 11B, A2 (2011)
V. Berthé, J. Bourdon, T. Jolivet, A. Siegel, A combinatorial approach to products of Pisot substitutions. Ergodic Theory Dyn. Syst. 36(6), 1757–1794 (2016)
V. Berthé, J. Cassaigne, W. Steiner, Balance properties of Arnoux-Rauzy words. Int. J. Algebra Comput. 23(4), 689–703 (2013)
V. Berthé, V. Delecroix, Beyond substitutive dynamical systems: S-adic expansions. RIMS Lecture Note ‘Kôkyûroku Bessatsu’ B46, 81–123 (2014)
V. Berthé, E. Domenjoud, D. Jamet, X. Provençal, Fully subtractive algorithm, tribonacci numeration and connectedness of discrete planes, in Numeration and Substitution 2012. RIMS Kôkyûroku Bessatsu, vol. B46 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2014), pp. 159–174
V. Berthé, S. Ferenczi, L.Q. Zamboni, Interactions between dynamics, arithmetics and combinatorics: the good, the bad, and the ugly, in Algebraic and Topological Dynamics. Contemp. Math., vol. 385 (American Mathematical Society, Providence, RI, 2005), pp. 333–364
V. Berthé, C. Holton, L.Q. Zamboni, Initial powers of Sturmian sequences. Acta Arith. 122(4), 315–347 (2006)
V. Berthé, T. Jolivet, A. Siegel, Substitutive Arnoux-Rauzy sequences have pure discrete spectrum. Unif. Distrib. Theory 7(1), 173–197 (2012)
V. Berthé, S. Labbé, Factor complexity of S-adic words generated by the Arnoux-Rauzy-Poincaré algorithm. Adv. Appl. Math. 63, 90–130 (2015)
V. Berthé, M. Minervino, W. Steiner, J. Thuswaldner, The S-adic Pisot conjecture on two letters. Topology Appl. 205, 47–57 (2016)
V. Berthé, A. Siegel, J.M. Thuswaldner, Substitutions, Rauzy fractals, and tilings, in Combinatorics, Automata and Number Theory. Encyclopedia of Mathematics and its Applications, vol. 135 (Cambridge University Press, Cambridge, 2010)
V. Berthé, W. Steiner, J.M. Thuswaldner, Geometry, dynamics, and arithmetic of S-adic shifts. Ann. Inst. Fourier (Grenoble) 69(3), 1347–1409 (2019)
S. Bezuglyi, J. Kwiatkowski, K. Medynets, B. Solomyak, Invariant measures on stationary Bratteli diagrams. Ergodic Theory Dyn. Syst. 30(4), 973–1007 (2010)
S. Bezuglyi, J. Kwiatkowski, K. Medynets, B. Solomyak, Finite rank Bratteli diagrams: structure of invariant measures. Trans. Am. Math. Soc. 365(5), 2637–2679 (2013)
G. Birkhoff, Extensions of Jentzsch’s theorem. Trans. Am. Math. Soc. 85, 219–227 (1957)
M. Boshernitzan, A unique ergodicity of minimal symbolic flows with linear block growth. J. Anal. Math. 44, 77–96 (1984/85)
P. Boyland, W. Severa, Geometric representation of the infimax S-adic family. Fundam. Math. 240(1), 15–50 (2018)
A.J. Brentjes, Multidimensional continued fraction algorithms, Mathematical Centre Tracts, vol. 145 (Mathematisch Centrum, Amsterdam, 1981)
V. Brun, Algorithmes euclidiens pour trois et quatre nombres, in Treizième congrès des mathèmaticiens scandinaves, tenu à Helsinki 18-23 août 1957 (Mercators Tryckeri, Helsinki, 1958), pp. 45–64
E.B. Burger, J. Gell-Redman, R. Kravitz, D. Walton, N. Yates, Shrinking the period lengths of continued fractions while still capturing convergents. J. Number Theory 128(1), 144–153 (2008)
V. Canterini, A. Siegel, Geometric representation of substitutions of Pisot type. Trans. Am. Math. Soc. 353(12), 5121–5144 (2001)
J. Cassaigne, S. Ferenczi, A. Messaoudi, Weak mixing and eigenvalues for Arnoux-Rauzy sequences. Ann. Inst. Fourier (Grenoble) 58(6), 1983–2005 (2008)
J. Cassaigne, S. Ferenczi, L.Q. Zamboni, Imbalances in Arnoux-Rauzy sequences. Ann. Inst. Fourier (Grenoble) 50(4), 1265–1276 (2000)
J. Cassaigne, S. Labbé, J. Leroy, A set of sequences of complexity 2n + 1, in Combinatorics on Words. Lecture Notes in Comput. Sci., vol. 10432 (Springer, Cham, 2017), pp. 144–156
J. Cassaigne, F. Nicolas, Factor complexity, in: Combinatorics, Automata and Number Theory. Encyclopedia Math. Appl., vol. 135 (Cambridge University Press, Cambridge, 2010), pp. 163–247
M.I. Cortez, F. Durand, B. Host, A. Maass, Continuous and measurable eigenfunctions of linearly recurrent dynamical Cantor systems. J. Lond. Math. Soc. (2) 67(3), 790–804 (2003)
E.M. Coven, G.A. Hedlund, Sequences with minimal block growth. Math. Systems Theory 7, 138–153 (1973)
V. Delecroix, T. Hejda, W. Steiner, Balancedness of Arnoux-Rauzy and Brun words, in WORDS. Lecture Notes in Computer Science, vol. 8079, pp. 119–131 (Springer, Berlin, 2013)
R. DeLeo, I.A. Dynnikov, Geometry of plane sections of the infinite regular skew polyhedron {4, 6∣4}. Geom. Dedicata 138, 51–67 (2009)
J.M. Dumont, A. Thomas, Systemes de numeration et fonctions fractales relatifs aux substitutions. Theor. Comput. Sci. 65(2), 153–169 (1989)
F. Durand, Linearly recurrent subshifts have a finite number of non-periodic subshift factors. Ergodic Theory Dyn. Syst. 20, 1061–1078 (2000)
F. Durand, Corrigendum and addendum to: “Linearly recurrent subshifts have a finite number of non-periodic subshift factors” [Ergodic Theory Dynam. Systems 20 (2000), no. 4, 1061–1078]. Ergodic Theory Dyn. Syst. 23, 663–669 (2003)
F. Durand, J. Leroy, G. Richomme, Do the properties of an S-adic representation determine factor complexity? J. Integer Seq. 16(2), Article 13.2.6, 30 pp. (2013)
H. Ei, Some properties of invertible substitutions of rank d, and higher dimensional substitutions. Osaka J. Math. 40(2), 543–562 (2003)
H. Ei, S. Ito, H. Rao, Atomic surfaces, tilings and coincidences. II. Reducible case. Ann. Inst. Fourier (Grenoble) 56(7), 2285–2313 (2006). Numération, pavages, substitutions
M. Einsiedler, T. Ward, Ergodic Theory with a View Towards Number Theory. Graduate Texts in Mathematics, vol. 259 (Springer, London, 2011)
S. Ferenczi, Rank and symbolic complexity. Ergodic Theory Dyn. Syst. 16(4), 663–682 (1996)
S. Ferenczi, A.M. Fisher, M. Talet, Minimality and unique ergodicity for adic transformations. J. Anal. Math. 109, 1–31 (2009)
T. Fernique, Multidimensional Sturmian sequences and generalized substitutions. Int. J. Found. Comput. Sci. 17(3), 575–599 (2006)
T. Fernique, Generation and recognition of digital planes using multi-dimensional continued fractions, in Discrete Geometry for Computer Imagery. Lecture Notes in Comput. Sci., vol. 4992 (Springer, Berlin, 2008)
A.M. Fisher, Nonstationary mixing and the unique ergodicity of adic transformations. Stochastics Dyn. 9(3), 335–391 (2009)
N.P. Fogg, Substitutions in Dynamics, Arithmetics and Combinatorics. Lecture Notes in Mathematics, vol. 1794 (Springer, Berlin, 2002)
T. Fujita, S. Ito, M. Keane, M. Ohtsuki, On almost everywhere exponential convergence of the modified Jacobi-Perron algorithm: a corrected proof. Ergodic Theory Dyn. Syst. 16(6), 1345–1352 (1996)
H. Furstenberg, Stationary Processes and Prediction Theory. Annals of Mathematics Studies, No. 44 (Princeton University Press, Princeton, NJ, 1960)
P.R. Halmos, Lectures on Ergodic Theory (Chelsea Publishing Co., New York, 1960)
C. Holton, L.Q. Zamboni, Geometric realizations of substitutions. Bull. Soc. Math. France 126(2), 149–179 (1998)
J.E. Hopcroft, J.D. Ullman, Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Series in Computer Science (Addison-Wesley Publishing Co., Reading, MA, 1979).
P. Hubert, A. Messaoudi, Best simultaneous Diophantine approximations of Pisot numbers and Rauzy fractals. Acta Arith. 124(1), 1–15 (2006)
S. Ito, M. Kimura, On Rauzy fractal. Japan J. Ind. Appl. Math. 8(3), 461–486 (1991)
S. Ito, M. Ohtsuki, Parallelogram tilings and Jacobi-Perron algorithm. Tokyo J. Math. 17(1), 33–58 (1994)
S. Ito, H. Rao, Atomic surfaces, tilings and coincidence. I. Irreducible case. Israel J. Math. 153, 129–155 (2006)
D. Jamet, N. Lafrenière, X. Provençal, Generation of digital planes using generalized continued-fractions algorithms, in Discrete Geometry for Computer Imagery. Lecture Notes in Comput. Sci., vol. 9647, pp. 45–56 (Springer, Cham, 2016)
D. Jamet, J.L. Toutant, On the connectedness of rational arithmetic discrete hyperplanes, in Discrete Geometry for Computer Imagery. Lecture Notes in Comput. Sci., vol. 4245, (Springer, Berlin, 2006), pp. 223–234
A. Katok, Interval exchange transformations and some special flows are not mixing. Israel J. Math. 35(4), 301–310 (1980)
S. Labbé, 3-dimensional continued fraction algorithms cheat sheets (2015). http://arxiv.org/abs/1511.08399
J. Lagarias, Y. Wang, Self-affine tiles in \(\mathbb {R}^n\). Adv. Math. 121, 21–49 (1996)
J. Leroy, Some improvements of the S-adic conjecture. Adv. Appl. Math. 48(1), 79–98 (2012)
J. Leroy, An S-adic characterization of minimal subshifts with first difference of complexity 1 ≤ p(n + 1) − p(n) ≤ 2. Discrete Math. Theor. Comput. Sci. 16(1), 233–286 (2014)
G. Levitt, La dynamique des pseudogroupes de rotations. Invent. Math. 113(3), 633–670 (1993)
B. Loridant, M. Minervino, Geometrical models for a class of reducible Pisot substitutions. Discrete Comput. Geom. 60, 981–1028 (2018)
M. Lothaire, Algebraic Combinatorics on Words. Encyclopedia of Mathematics and its Applications, vol. 90 (Cambridge University Press, Cambridge, 2002). A collective work by J. Berstel, D. Perrin, P. Seebold, J. Cassaigne, A. De Luca, S. Varricchio, A. Lascoux, B. Leclerc, J.-Y. Thibon, V. Bruyere, C. Frougny, F. Mignosi, A. Restivo, C. Reutenauer, D. Foata, G.-N. Han, J. Desarmenien, V. Diekert, T. Harju, J. Karhumaki and W. Plandowski, with a preface by J. Berstel and D. Perrin
R. Meester, A simple proof of the exponential convergence of the modified Jacobi-Perron algorithm. Ergodic Theory Dyn. Syst. 19(4), 1077–1083 (1999)
A. Messaoudi, Frontière du fractal de Rauzy et système de numération complexe. Acta Arith. 95(3), 195–224 (2000)
A. Messaoudi, Propriétés arithmétiques et topologiques d’une classe d’ensembles fractales. Acta Arith. 121(4), 341–366 (2006)
M. Minervino, W. Steiner, Tilings for Pisot beta numeration. Indag. Math. (N.S.) 25(4), 745–773 (2014)
M. Minervino, J.M. Thuswaldner, The geometry of non-unit Pisot substitutions. Ann. Inst. Fourier (Grenoble) 64(4), 1373–1417 (2014)
M. Morse, G.A. Hedlund, Symbolic dynamics II. Sturmian trajectories. Am. J. Math. 62, 1–42 (1940)
H. Nakada, S. Ito, S. Tanaka, On the invariant measure for the transformations associated with some real continued-fractions. Keio Eng. Rep. 30(13), 159–175 (1977)
O. Perron, Grundlagen für eine Theorie des Jacobischen Kettenbruchalgorithmus. Math. Ann. 64(1), 1–76 (1907)
M. Queffélec, Substitution Dynamical Systems—Spectral Analysis. Lecture Notes in Mathematics, vol. 1294, 2nd edn. (Springer, Berlin, 2010)
C. Radin, M. Wolff, Space tilings and local isomorphism. Geom. Dedicata 42(3), 355–360 (1992)
G. Rauzy, Une généralisation du développement en fraction continue, in Séminaire Delange-Pisot-Poitou, 18e année: 1976/77, Théorie des nombres, Fasc. 1, pp. Exp. No. 15, 16 (Secrétariat Math., Paris, 1977)
G. Rauzy, échanges d’intervalles et transformations induites. Acta Arith. 34(4), 315–328 (1979)
G. Rauzy, Nombres algébriques et substitutions. Bull. Soc. Math. France 110(2), 147–178 (1982)
J.P. Reveillès, Géométrie discrète, calculs en nombres entiers et algorithmes. Ph.D. thesis, Université Louis Pasteur, Strasbourg (1991)
V.A. Rohlin, Exact endomorphism of a Lebesgue space. Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. 14, 443–474 (1964)
Y. Sano, P. Arnoux, S. Ito, Higher dimensional extensions of substitutions and their dual maps. J. Anal. Math. 83, 183–206 (2001)
B.R. Schratzberger, The exponent of convergence for Brun’s algorithm in two dimensions. Österreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 207, 229–238 (1999) (1998)
F. Schweiger, Multidimensional Continued Fractions Oxford Science Publications (Oxford University Press, Oxford, 2000)
E.S. Selmer, Continued fractions in several dimensions. Nordisk Nat. Tidskr. 9, 37–43, 95 (1961)
C. Series, The modular surface and continued fractions. J. London Math. Soc. (2) 31(1), 69–80 (1985)
A. Siegel, Représentation des systèmes dynamiques substitutifs non unimodulaires. Ergodic Theory Dyn. Syst. 23(4), 1247–1273 (2003)
A. Siegel, J.M. Thuswaldner, Topological properties of Rauzy fractals. Mém. Soc. Math. Fr. (N.S.) 118, 144pp (2009)
V.F. Sirvent, Y. Wang, Self-affine tiling via substitution dynamical systems and Rauzy fractals. Pac. J. Math. 206(2), 465–485 (2002)
M. Viana, Ergodic theory of interval exchange maps. Rev. Mat. Complut. 19(1), 7–100 (2006)
P. Walters, An Introduction to Ergodic Theory. Graduate Texts in Mathematics, vol. 79 (Springer, New York, 1982)
Acknowledgements
I warmly thank Shigeki Akiyama and Pierre Arnoux for inviting me to contribute to this volume. I very much appreciate their constant encouragement and support, and the many discussions I had with them. Moreover, I am indebted to Valérie Berthé, Sébastien Labbé, and Wolfgang Steiner for their suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Thuswaldner, J.M. (2020). S-adic Sequences: A Bridge Between Dynamics, Arithmetic, and Geometry. In: Akiyama, S., Arnoux, P. (eds) Substitution and Tiling Dynamics: Introduction to Self-inducing Structures. Lecture Notes in Mathematics, vol 2273. Springer, Cham. https://doi.org/10.1007/978-3-030-57666-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-57666-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57665-3
Online ISBN: 978-3-030-57666-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


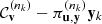 are said to be close to each other if Γ(v) and
are said to be close to each other if Γ(v) and