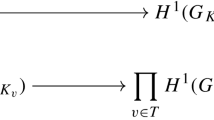Abstract
The algebraic intersection theory on a smooth projective variety X over a field is a classical topic. Given two subvarieties Y and Z in X, with complementary dimensions, one defines an integer Y.Z, their algebraic intersection number.
At the beginning of the seventies, Arakelov defined an arithmetic intersection theory on a regular integral model X of a curve over a number field. Given two divisors Y and Z in X, he defines a real number, the arithmetic intersection of Y and Z.
The goal of this chapter is to extend Arakelov theory to higher dimensions. More precisely, given a regular projective scheme X over the integers and an hermitian line bundle \(\bar {L}\) on X, to any closed subset Y ⊂ X is attached a real number \(h_{\bar {L}}(Y)\), the Faltings height of Y . Our definition is given by a list of axioms.
In a last paragraph we develop, without proofs, an arithmetic intersection theory for X, in terms of arithmetic Chow groups. We also explain how to view \(h_{\bar {L}}(Y)\) as an intersection number.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
S.Y. Arakelov, Intersection theory of divisors on an arithmetic surface. Izv. Akad. Nauk SSSR Ser. Mat. 38, 1179–1192 (1974)
J.-B. Bost, H. Gillet, C. Soulé, Heights of projective varieties and positive Green forms. J. Amer. Math. Soc. 7, 903 (1994)
N. Bourbaki, Algèbre commutative IV, Eléments de Mathématique (Hermann, Paris)
N. Bourbaki, Algèbre I, Eléments de Mathématique (Hermann, Paris)
N. Bourbaki, Algèbre II, Eléments de Mathématique (Hermann, Paris)
G. Faltings, Diophantine approximation on abelian varieties. Ann. Math. (2) 133, 549–576 (1991)
H. Gillet, K-theory and intersection theory, in Handbook of K-theory, ed. by E.M. Friedlander, D.R. Grayson (Springer, New York, 2005), pp. 235–294
H. Gillet, C. Soulé, Intersection theory using Adams operations. Invent. Math. 90, 243–277 (1987)
H. Gillet, C. Soulé, Arithmetic intersection theory. Inst. Hautes études Sci. Publ. Math. 72, 93–174 (1990)
Q. Liu, Algebraic Geometry and Arithmetic Curves. Oxford Graduate Texts in Mathematics (Oxford University Press, Oxford, 2002)
C. Soulé, D. Abramovich, J.-F. Burnol, J. Kramer, Lectures on Arakelov Geometry (Cambridge University Press, Cambridge, 1991)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Soulé, C. (2021). Chapter I: Arithmetic Intersection. In: Peyre, E., Rémond, G. (eds) Arakelov Geometry and Diophantine Applications. Lecture Notes in Mathematics, vol 2276. Springer, Cham. https://doi.org/10.1007/978-3-030-57559-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-57559-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57558-8
Online ISBN: 978-3-030-57559-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)