Abstract
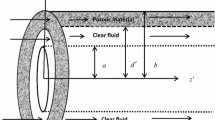
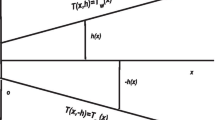
The use of velocity and temperature distributions in moving fluids is of theoretical and practical significance. Designing efficient heat exchange equipment, development of modes of thermal and thermomechanical processing of products, determination of heat losses in pipeline systems is related to the need to determine the velocity and temperature fields in the flows of fluids and gases. This article presents the development results of an approximate analytical method for mathematical modeling of heat transfer process in laminar flows. The main provisions of the method are demonstrated using the example of solving the heat exchange problem in a plane parallel channel. The combined use of the thermal balance integral method and location method allowed obtaining a simple in form analytical solution of the problem under study. Note that accuracy of the solutions obtained depends on the number of approximations performed, i.e. on the number of N (points of a spatial variable), in which the initial differential equation is satisfied exactly. So, already at \( N = 2 \), a ratio error is not more than 10% in the range of changes along the longitudinal coordinate \( 0.1 \le\upeta < \infty \) and at \( N = 10 \) decreases to 1%. Analytical form of the resulting solutions allows one to analyze isotherm fields inside the channel, to calculate the dimensionless values of the average mass temperature, the Nusselt number, etc.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Landau, L.D., Lifshitz, E.M.: Fluid Mechanics, 2nd edn. Pergamon Press, Headington Hill Hall (1987)
Kays, W.M., Crawford, M.E.: Convective Heat and Mass Transfer, 2nd edn. McGraw–Hill, New York (1993)
Sneddon, I.N.: Fourier Transforms. Dover Publications, New York (1995)
Cherati, D.Y., Ghasemi-Fare, O.: Analyzing transient heat and moisture transport surrounding a heat source in unsaturated porous media using the Green’s function. Geothermics 81, 224–234 (2019). https://doi.org/10.1016/j.geothermics.2019.04.012
Tranter, C.J.: Integral Transforms in Mathematical Physics. Methuen, London (1966)
Tsoi, P.V.: System Methods for Calculating Boundary-Value Problems of Heat and Mass Transfer, 3rd edn. Publishing House MPEI, Moscow (2005)
Christie, I., Griffiths, D.F., Mitchell, A.R., Zienkiewicz, O.C.: Finite element methods for second order differential equations with significant first derivatives. Int. J. Numer. Meth. Eng. 10(6), 1389–1396 (1976)
Layeni, O.P., Johnson, J.V.: Hybrids of the heat balance integral method. Appl. Math. Comput. 218(14), 7431–7444 (2012). https://doi.org/10.1016/j.amc.2012.01.001
Mitchell, S.L., Myers, T.G.: Improving the accuracy of heat balance integral methods applied to thermal problems with time dependent boundary conditions. Int. J. Heat Mass Transf. 53(17–18), 3540–3551 (2010). https://doi.org/10.1016/j.ijheatmasstransfer.2010.04.015
Mitchell, S.L., Myers, T.G.: Application of standard and refined heat balance integral methods to one-dimensional Stefan problems. SIAM Rev. 52(1), 57–86 (2010). https://doi.org/10.1137/080733036
Novozhilov, V.: Application of heat-balance integral method to conjugate thermal explosion. Therm. Sci. 13(2), 73–80 (2009). https://doi.org/10.2298/tsci0902073n
Dutta, S., Sil, A.N., Saha, J.K., Mukherjee, T.K.: Ritz variational method for the high-lying non-autoionizing doubly excited 1,3Fe states of two-electron atoms. Int. J. Quantum Chem. 118(14), e25577 (2017). https://doi.org/10.1002/qua.25577
Lotfi, A., Yousef, S.A.: A generalization of ritz-variational method for solving a class of fractional optimization problems. J. Optim. Theory Appl. 174(1), 238–255 (2017). https://doi.org/10.1007/s10957-016-0912-3
Falk, R.S.: Ritz method based on a complementary variational principle. Revue francaise d automatique, informatique, recherché operationnelle 10(8), 39–48 (1976). https://doi.org/10.1051/m2an/197610r200391
Kantorovich, L.V.: A method for the approximate solution of partial differential equations. Doklady AN SSSR 2(9), 532–534 (1934)
Rao, T.D., Chakraverty, S.: Modeling radon diffusion equation in soil pore matrix by using uncertainty based orthogonal polynomials in Galerkin’s method. Coupled Syst. Mech. 6(4), 487–499 (2017). https://doi.org/10.12989/csm.2017.6.4.487
Nourgaliev, R., Luo, H., Weston, B., Anderson, A., Schofield, S., Dunn, T., Delplanque, J.R.: Fully-implicit orthogonal reconstructed discontinuous Galerkin method for fluid dynamics with phase change. J. Comput. Phys. 305, 964–996 (2016). https://doi.org/10.1016/j.jcp.2015.11.004
Belytschko, T., Lu, Y.Y., Gu, L.: Element free Galerkin methods. Int. J. Numer. Methods Eng. 37(2), 229–256 (1994). https://doi.org/10.1002/nme.1620370205
Arnold, D.N., Brezzi, F., Cockburn, B., Marini, D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2001). https://doi.org/10.1137/s0036142901384162
Letelier, M.F., Hinojosa, C.B., Siginer, D.A.: Analytical solution of the Graetz problem for non–linear viscoelastic fluids in tubes of arbitrary cross–section. Int. J. Therm. Sci. 111, 369–378 (2017). https://doi.org/10.1016/j.ijthermalsci.2016.05.034
Bennett, T.D.: Correlations for the Graetz problem in convection. Int. J. Heat Mass Transf. 136, 832–841 (2019). https://doi.org/10.1016/j.ijheatmasstransfer.2019.03.006
Eremin, A.V.: Study of thermal exchange with liquid flowing in a cylindrical channel. In: International Science and Technology Conference, pp. 1–5 (2019). https://doi.org/10.1109/EastConf.2019.8725422
Eremin, A.V., Kudinov, V.A., Stefanyuk, E.V.: Heat exchange in a cylindrical channel with stabilized laminar fluid flow. Fluid Dyn. 53, 29–39 (2018). https://doi.org/10.1134/s0015462818040171
Kudinov, V.A., Eremin, A.V., Kudinov, I.V.: The development and investigation of a strongly non–equilibrium model of heat transfer in fluid with allowance for the spatial and temporal non-locality and energy dissipation. Thermophys. Aeromech. 24(6), 901–907 (2017). https://doi.org/10.1134/s0869864317060087
Fedorov, F.M.: Boundary Method for Solving Applied Problems of Mathematical Physics. Nauka, Novosibirsk (2000)
Eremin, A.V., Kudinov, I.V., Dovgyallo, A.I., Kudinov, V.A.: Heat exchange in a liquid with energy dissipation. J. Eng. Phys. Thermophys. 90(5), 1234–1242 (2017). https://doi.org/10.1007/s10891-017-1679-6
Kudinov, I.V., Kudinov, V.A., Kotova, E.V., Eremin, A.V.: On one method of solving nonstationary boundary-value problems. J. Eng. Phys. Thermophys. 90(6), 1317–1327 (2017). https://doi.org/10.1007/s10891-017-1689-4
Petuhov, B.S.: Heat Transfer and Resistance During Laminar Fluid Flow in Pipes. Energy, Moscow (1967)
Acknowledgment
The reported study was funded by RFBR, project number 20-38-70021 and the Council on grants of the President of the Russian Federation as part of the research, project number MK-2614.2019.8.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Eremin, A., Gubareva, K. (2021). Approximate Analytical Method for Solving the Heat Transfer Problem in a Flat Channel. In: Murgul, V., Pukhkal, V. (eds) International Scientific Conference Energy Management of Municipal Facilities and Sustainable Energy Technologies EMMFT 2019. EMMFT 2019. Advances in Intelligent Systems and Computing, vol 1259. Springer, Cham. https://doi.org/10.1007/978-3-030-57453-6_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-57453-6_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57452-9
Online ISBN: 978-3-030-57453-6
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)