Hyperplane Arrangements in polymake

Abstract

Hyperplane arrangements form the latest addition to the zoo of combinatorial objects dealt with by polymake. We report on their implementation and on a algorithm to compute the associated cell decomposition. The implemented algorithm performs significantly better than brute force alternatives, as it requires fewer convex hulls computations. The implementation is included in polymake since release 4.0.

Research by L. Kastner is supported by Deutsche Forschungsgemeinschaft (SFB-TRR 195: “Symbolic Tools in Mathematics and their Application”).

1 Introduction

Hyperplane arrangements are ubiquitous objects appearing in different areas of mathematics such as discrete geometry, algebraic combinatorics and algebraic geometry. A common theme is to understand the combinatorics and the topology of the cells in the complement of the arrangement. Combinatorics and its connections to other areas of mathematics are the focus of the software framework polymake [GJ00], hence hyperplane arrangements form an almost mandatory addition to the objects available. We will discuss the implementation, such as the datatypes and properties, as well as some basic algorithms for analyzing hyperplane arrangements.

One of the main advantages of polymake are its various interfaces to other software. This allows keeping the codebase slim, while using powerful software developed by experts from other fields. Still polymake provides basic algorithms for many tasks, in case other software is not available. Hence the idea of the hyperplane arrangements is to provide a datatype with basic functionality as a basis for future interfaces to other software, e.g. to ZRAM [Brü+99] for computing the cell decomposition from the hyperplanes. Nevertheless, the polymake implementation of hyperplane arrangements comes with a basic algorithm for computing the associated cell decomposition that performs significantly better than brute force alternatives. Thus, we will discuss the main ideas of this algorithm in this article as well.

The combinatorics of hyperplane arrangements in real space is linked to zonotopes. Each arrangement endows the support space with a fan structure which is the normal fan of a zonotope. Each hyperplane subdivides the space in two halfspaces. Therefore we can encode relative positions of points with respect to the arrangement. In other words, hyperplane arrangements are examples of (oriented) matroids. Moreover, the hyperplanes in an arrangement can be seen as mirrors hyperplanes of a reflection group.

An interesting application is in Geometric Invariant Theory. GIT constructs quotients of algebraic varieties modulo group actions. The quotients depend on the choice of a linearized ample line bundle. Variation of geometric invariant theory quotients studies how quotients vary when changing the line bundle. Under some hypothesis the classes of equivalent quotients are convex subsets, called chambers. The walls among chambers are defined by certain hyperplane arrangements, see [DH98, Example 3.3.24].

2 Main Definitions

We begin with the basic definitions in the theory of hyperplane arrangements following our implementation in polymake.

Definition 1

A hyperplane arrangement $H=(H,{\mathcal {S}}_H)$ in $\mathbb {R}^d$ is given by the following data:

• 1. a finite set of linear forms encoding hyperplanes $H = \big \{h \in \mathbb R^d \setminus \{0\}\big \}$ and

• 2. a polyhedral cone ${\mathcal {S}}_H\subseteq \mathbb R^d$ which we call the support cone.

Given a hyperplane arrangement H, the induced fan ${\varSigma }_H$ is a fan with support ${\mathcal {S}}_H$ given by subdividing ${\mathcal {S}}_H$ along all $\{x \in \mathbb R^d \, | \, \langle x,h \rangle =0\}$ for $h \in H$.

Every hyperplane in the arrangement subdivides the space into two halfspaces

$$ h^+\ :=\ \{x\in \mathbb R^d \, | \, \langle x,h \rangle > 0\} \text{ and } h^-\ :=\ \{x\in \mathbb R^d\, | \, \langle x,h \rangle < 0\}. $$

We remark that in the definition we allow duplicate hyperplanes, but from each hyperplane arrangement we can construct a reduced one. Let H be a hyperplane arrangement given by the hyperplanes $\{h_1, h_2, \dots , h_n\}$. The reduced hyperplane arrangement $H_{\text {red}}$ has the same support cone as H and $h_i \in H_{\text {red}}$ if and only if $h_i \not = \lambda b$, for any $\lambda \in \mathbb R$ and any $b \in \{h_1, \dots , h_{i-1}\}$.

To a hyperplane arrangement $H=\{h_1,\ldots ,h_n\}\subseteq \mathbb R^d$ we associate the polytope

$$ {\mathcal {Z}}_H\ :=\ \sum _{i=1}^n \, [-h_i,h_i]+{\mathcal {S}}_H^{\vee }, $$

the Minkowski sum of all the line segments $[-h_i,h_i]$ and the dual support cone ${\mathcal {S}}_H^{\vee }$. If ${\mathcal {S}}_H=\mathbb R^d$, then ${\mathcal {S}}_H^{\vee }=0$ and ${\mathcal {Z}}_H$ is a zonotope.

Remark 1

Often hyperplane arrangements are defined without a support cone, i.e. only for the case ${\mathcal {S}}_H=\mathbb R^d$. The connection between intersecting ${\varSigma }_H\cap {\mathcal {S}}_H$ is done via taking the Minkowski sum ${\mathcal {Z}}_H+{\mathcal {S}}_H^{\vee }$ on the dual side. The main ingredient is the fact that

$$ (\sigma +\tau )^\vee \ =\ \sigma ^\vee \cap \tau ^\vee $$

holds for two cones $\sigma$ and $\tau$.

Proposition 2.1

[Zie95, Thm. 7.16] The fan ${\varSigma }_H$ is the normal fan of ${\mathcal {Z}}_H$.

Definition 2

To a maximal cone $\sigma \in {\varSigma }_H$ we associate its signature, which is a set $\mathrm {sig}(\sigma ):=\big \{i\in \{1,\ldots ,n\}\ |\ \sigma \subseteq \overline{h_i^+}\big \}$.

Remark 2

In polymake release 4.0 the signature was defined as the set of indices such that $\sigma \subseteq \overline{h_i^-}$. The signature will be automatically updated for data saved in polymake 4.0 and loaded in the subsequent releases.

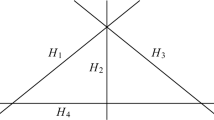
Example 1

Let H be given by

$$ H\ =\ \{(0,1),(1,1),(-2,1)\}\ \subseteq \mathbb R^2. $$

We will have a look at the induced fans for different support cones ${\mathcal {S}}_H$. The fan ${\varSigma }_H$ and the polytope ${\mathcal {Z}}_H$ are visualized in Fig. 1 for varying ${\mathcal {S}}_H$.

Fig. 1.

Visualization of ${\varSigma }_H$ and ${\mathcal {Z}}_H$ for Example 1

In each of the pictures, the support cone is indicated as the shaded area. The structure of the fan ${\varSigma }_H$ depends heavily on the support cone ${\mathcal {S}}_H$. In particular, it is possible for hyperplanes to only intersect ${\mathcal {S}}_H$ trivially and thereby becoming irrelevant for ${\varSigma }_H$. Thus, one may loose information when going from H to ${\varSigma }_H$.

The labels at the hyperplanes in the first picture indicate which side constitutes $h^+$, $h^-$ respectively. Using these one can read of the signatures of the single cells, for example the cell $\sigma$ generated by the rays (1, 0) and (1, 2) has signature $\mathrm {sig}(\sigma )=\{1,2\}$.

2.1 Affine Hyperplane Arrangements

An affine hyperplane arrangement is usually given by a finite set of affine hyperplanes:

$$ H_{\text {aff}}\ :=\ \{[a,b]\in \mathbb R^{d}\times \mathbb R\}. $$

The whole space $\mathbb R^d$ is then subdivided along the hyperplanes

$$ \{x\in \mathbb R^d\, |\, \langle a,x \rangle =b\}, \text{ for } \text{ all } [a,b]\in H, $$

resulting in a polyhedral complex ${{\,\mathrm{\mathcal {PC}}\,}}_{H_{\text {aff}}}\subseteq \mathbb R^d$.

Analogously to the connection between polytopes and cones, or polyhedral complexes and fans, every affine hyperplane arrangement gives rise to a (projective) hyperplane arrangement by embedding it at height 1:

$$ H_{\text {proj}}\ :=\ \{[-b,a]\ |\ [a,b]\in H\}. $$

If we intersect the fan ${\varSigma }_{H_{\text {proj}}}$ with the affine hyperplane $[x_0=1]\subseteq \mathbb R^{d+1}$, the resulting polyhedral complex is isomorphic to ${{\,\mathrm{\mathcal {PC}}\,}}_{H_{\text {aff}}}$, via the embedding $\mathbb R^d\rightarrow \mathbb R^{d+1}$, $x\mapsto [1,x]$.

The support cone allows one to deal with affine hyperplanes computationally. Set

$$ {\mathcal {S}}_{H_{\text {proj}}}\ :=\ \{[x_0,x_1,\ldots ,x_{d}]\in \mathbb R^{d+1}\ |\ x_0\ge 0\}, $$

then the maximal cones of ${\varSigma }_{H_{\text {proj}}}$ are in one-to-one correspondence with the maximal cells of ${{\,\mathrm{\mathcal {PC}}\,}}_{H_{\text {aff}}}$. In particular, polymake can interpret ${\varSigma }_{H_{\text {proj}}}$ as a polyhedral complex via the embedding mentioned above, and this polyhedral complex will be exactly ${{\,\mathrm{\mathcal {PC}}\,}}_{H_{\text {aff}}}$.

Example 2

As a simple example, choose the following hyperplanes in $\mathbb R^1$:

$$ \begin{array}{ccc} x_1=-1,&x_1=0,&x_1=2. \end{array} $$

The associated hyperplanes of $H_{\text {proj}}$ in $\mathbb R^2$ are exactly those of the hyperplane arrangement from Example 1. For ${\mathcal {S}}_H$ we choose the cone $\{x_0\ge 0\}$, then $H_{\text {aff}}$ will be at height one.

The induced affine hyperplane arrangement is indicated by the dots and thick line. It is one dimensional and the associated polyhedral complex ${{\,\mathrm{\mathcal {PC}}\,}}_{H_{\text {aff}}}$ has four maximal cells.

Example 3

The following is an example of code in polymake.

3 Implementation

Hyperplane arrangements are implemented in the software polymake as a new object HyperplaneArrangement, which is derived from the already existing object VectorConfiguration. We augment the existing properties of VectorConfiguration with the following properties and methods.

• 1. HYPERPLANES A matrix encoding the hyperplanes as rows, this is just an override of the property VECTORS of VectorConfiguration

• 2. SUPPORT A polymake Cone, denoting the support ${\mathcal {S}}_H$.

• 3. CELL_DECOMPOSITION A polymake PolyhedralFan, the cell decomposition ${\varSigma }_H$.

• 4. CELL_SIGNATURES A $\texttt {Array<Set<Int>>}$, the i-th set in the array contains the indices of hyperplanes evaluating positively on the i-th maximal cone of CELL_DECOMPOSITION.

• 5. signature_to_cell Given a signature as $\texttt {Set<Int>}$, get the maximal cone with this signature, if it exists.

• 6. cell_to_signature Given a cell, a maximal cone of CELL_DECOMPOSITION, determine its signature.

3.1 Cell Decomposition Algorithm

Given $H=\{h_1,\ldots ,h_n\}$, we want to compute the subdivision of ${\mathcal {S}}_H$ induced by the hyperplanes, the induced fan ${\varSigma }_H$. This means, we want to find all the rays and maximal cones of ${\varSigma }_H$. In terms of the zonotope ${\mathcal {Z}}_H$, this is equivalent to knowing the facets and vertices of ${\mathcal {Z}}_H$, see [Fuk04, GS93]. The facet directions of ${\mathcal {Z}}_H$ are the rays of ${\varSigma }_H$. For very vertex of ${\mathcal {Z}}_H$ we get a maximal cone by determining which facets contain it.

The brute force approach is to loop over all possible signatures in $s\in 2^{\{1,\ldots ,n\}}$ and for every signature s to build the cone

$$ \bigcap _{i\in s}\overline{h_i^+}\ \cap \ \bigcap _{i\notin s}\overline{h_i^-}\ \cap \ {\mathcal {S}}_H. $$

For comparing the different algorithms, we count the number of times they have to perform a convex hull computation for converting a signature to a cone. There are $2^{n}$ signatures, so we have to perform $2^{n}$ convex hull computations. As we saw in Example 1, it can happen that some hyperplanes are irrelevant, either completely or just for single cells. Furthermore, in Example 1 the fan ${\varSigma }_H$ had at most six maximal cones, however we would have to compute eight intersections with the brute force approach regardless.

Remark 3

This brute force approach is in some ways parallel to the brute force approach for computing the Minkowski sum making up ${\mathcal {Z}}_H$, by taking considering all possible sums of the endpoints of the line segments. One arrives at $2^{n}$ points whose convex hull is ${\mathcal {Z}}_H$. There are several ways to go on: either attempt a massive convex hull computation directly, or check each point individually whether it is a vertex.

Our approach is to first find a full-dimensional cone $\sigma$ of ${\varSigma }_H$ and then to flip hyperplanes in order to compute its neighbors. First take a facet f of $\sigma$, then set

$$ \mathrm {sig}'\ :=\ (\mathrm {sig}(\sigma )\setminus \{i\in \mathrm {sig}(\sigma )\ |\ h_i||f\})\cup \{i\notin \mathrm {sig}(\sigma )\ |\ h_i||f\}), $$

where $h_i||f$ denotes that $h_i$ and f are parallel. This is the signature of the cell neighboring $\sigma$ at facet f, so we can use it to determine the rays of the neighboring cell. Finding the neighbors of a cell allows one to traverse the dual graph of the fan ${\varSigma }_H$. Taking the support cone ${\mathcal {S}}_H$ into account just requires some minor tweaks, like ignoring facets of $\sigma$ that are also facets of ${\mathcal {S}}_H$. By storing signatures one can avoid recomputation of cones.

To find a starting cone, one selects a generic point x from ${\mathcal {S}}_H$. A generic point will be contained in a maximal cone, this maximal cone will be

$$ \sigma (x)\ :=\ \bigcap _{i\ |\ x\in h_i^+}\overline{h_i^+}\ \cap \ \bigcap _{i\ |\ x\in h_i^-}\overline{h_i^-}. $$

The point x may be contained in some hyperplanes, but these hyperplanes are exactly those that also contain the entire ${\mathcal {S}}_H$. Using this approach we would do one convex hull computation per maximal cone, arriving at $\#\mathrm {maxcones}({\varSigma }_H)$ convex hull computations.

Remark 4

As the fan ${\varSigma }_H$ is polytopal, there is a reverse search structure on it, corresponding to the edge graph of the zonotope ${\mathcal {Z}}_H$. This has already been exploited by Sleumer in [Sle99] using the software framework [Brü+99]. Reverse search allows for different kinds of parallelisation and it would be interesting to study the performance of budgeted reverse search [AJ18, AJ16] on this particular problem. Note that the dual problem, finding the vertices of ${\mathcal {Z}}_H$, is equally hard, as it is a Minkowski sum with potentially many summands. We refer the reader to [GS93] for a detailed analysis.

3.2 Sample Code

We conclude with a few examples which illustrate the object HyperplaneArrangement and its properties. Example 6 reports the comparison between the running times of the new algorithm implemented in polymake and the brute force algorithm to compute cell decompositions.

Example 4

The following examples compute the $4! = 24$ cells in the Coxeter arrangement of type A3. The 6 linear hyperplanes in the arrangements are

$$ x_i - x_j = 0, \ \ 1 \le i < j \le 4. $$

Now we compute the 36 cells in the Linial arrangement [PS00] given by the 6 affine hyperplanes

$$ x_i - x_j = 1, \ \ 1 \le i < j \le 4. $$

As explained in Sect. 2.1, the support cone allows us to deal with affine hyperplanes. We transform the hyperplanes $[a,b] \in \mathbb R^4 \times \mathbb R$ in the projective arrangement $H_{\text {proj}}$ with hyperplanes $[-b,a]$ and then we intersect the latter with the support cone ${\mathcal {S}}_{H_{\text {proj}}}\ :=\ \{[x_0,x_1,\ldots ,x_{5}]\in \mathbb R^{5}\ |\ x_0\ge 0\}$ (Fig. 2).

Fig. 2.

The arrangement of type A3.

Example 5

This example is based on [Süß19]. Let X be a del Pezzo surface of degree 5 and $[K_X]$ the class of the canonical divisor. The cone of effective divisors $\overline{\text {Eff}}(X)$ is spanned by ten exceptional curves $[C_{ij}]$ indexed by $0 \le i<j \le 4$ and characterized by $[C_{ij}]^2=-1$ and $[C_{ij}]\cdot [K_Y]=-1$. Applying the change of basis $[C_{ij}] =b_i + b_j$, described in [Süß19, Section 3], we see that the polytope P given by points in $\overline{\text {Eff}}(X)$ intersecting $[K_X]$ with multiplicity $-1$ coincides with the hypersimplex $\varDelta (2,5)$. In the aforementioned article the author considers the cell decomposition of P induced by the hyperplane arrangement defined by

$$\begin{aligned} \{ [D] \in \overline{\text {Eff}}(X) \, | \, [D] \cdot [C_{ij}] =0\}. \end{aligned}$$

The decomposition is used to study the toric topology of the Grassmannian of planes in complex 5-dimensional space.

The following code allows one to compute the cell decomposition in polymake. We first compute the new pairing in the new basis $b_0, b_1, \dots , b_4$.

We then introduce the support cone given by the hypersimplex $\varDelta (2,5)$ in the new basis

Finally, we can compute the cell decomposition.

Example 6

Let H be the hyperplane arrangement in $\mathbb R^d$ given by the $2^d-1$ hyperplanes normal to $0/1$-vectors. The number of maximal cones in $\varSigma _H$ are known up to $d=8$, see entry A034997 in the Online Encyclopedia of Integer Sequences. We run polymake implementations of the BFS algorithm described above and the brute force alternative. Our results are reported in Table 1, where we can see that the BFS algorithm performs better than the brute force approach.

Table 1. Results and runtimes for arrangements in Example 6