Abstract
I present a version of Kit Fine’s stratified semantics for the logic RWQ and define a natural family of related structures called RW hyperdoctrines. After proving that RWQ is sound with respect to RW hyperdoctrines, we show how to construct, for each stratified model, a hyperdoctrine that verifies precisely the same sentences. Completeness of RWQ for hyperdoctrinal semantics then follows from completeness for stratified semantics, which is proved in an appendix. By examining the base category of RW hyperdoctrines, we find reason to be worried about the ontology of stratified models.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
For preliminaries on category theory, see e.g., [11].
- 2.
This can be fleshed out more, but it would take us too far afield to do so—the interested reader is referred to [22] for details.
- 3.
The Routley star was introduced by Routley and Routley in [21]. For more on how to interpret it, see [4] or [20]. An anonymous referee helpfully points out that there are precursors to the Routley star in the history of logic, some of which are helpfully surveyed in [5, Sects. 4.3–4.4]. Here, Dunn amusingly reports that [21] ‘more or less just springs [the star operator] on the reader’.
- 4.
Since
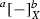 is a closure operator, we have that,
is a closure operator, we have that, 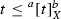 for all t; if \(t\le u\) then
for all t; if \(t\le u\) then 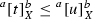 ; and
; and 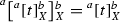 .
. - 5.
Context will in general suffice to determine whether we mean, e.g., \(I_X(x)\) or \(I_Y(x)\), and where context doesn’t so determine this feature guarantees that it doesn’t matter. So we will tend to just write I(x).
- 6.
Category-theorists often call conditions that make mention of features internal to the objects in a category evil. Both RH2 and RH4 have a bit too much ‘evil’ in them to win broad approbation from categorially-minded folks. I have a sneaking suspicion that they both conditions can, with proper reformulation of other parts of the theory, be avoided or at least made less evil, but have not been able to do so on my own to this point.
- 7.
The X’s contain the kind of information (viz. where in the hyperdoctrine one is doing the evaluating) that is easy to lose track of, so we will in general not omit them.
References
A.R. Anderson, N.D. Belnap, Entailment: The Logic of Relevance and Neccessity, vol. I (Princeton University Press, Princeton, 1975)
R.T. Brady, Natural deduction systems for some quantified relevant logics. Logique Et Analyse 27(108), 355–378 (1984)
R.T. Brady, Some concerns regarding ternary-relation semantics and truth-theoretic semantics in general. IfCoLog J. Logics their Appl. 4(3), 755–781 (2017)
J.M. Dunn, Star and perp: two treatments of negation. Philos. Perspect. 7, 331–357 (1993)
K. Fine, Models for entailment. J. Philos. Logic 3(4), 347–372 (1974)
K. Fine, Reasoning with Arbitrary Objects (Blackwell, Oxford, 1985)
K. Fine, Semantics for quantified relevance logic. J. Philos. Logic 17(1), 27–59 (1988)
K. Fine, Incompleteness for Quantified Relevance Logics. Directions in Relevant Logic (Springer, Berlin, 1989), pp. 205–225
K. Fine, N. Tennant, A defence of arbitrary objects. Proc. Aristotelian Soc., Suppl. Vol. 57, 55–89 (1983)
N. Galatos, P. Jipsen, T. Kowalski, H. Ono, Residuated Lattices: An Algebraic Glimpse at Substructural Logics (Elsevier, Amsterdam, 2007)
R.I. Goldblatt, Topoi: The Categorical Analysis of Logic (Dover Publications, 2006)
F.W. Lawvere, Adjointness in foundations. Dialectica 23(34), 281–296 (1969)
S.A. Logan, Notes on stratified semantics. J. Philos. Logic 48(4), 749–786 (2019)
E.D. Mares, Semantics for relevance logic with identity. Studia Logica 51(1), 1–20 (1992)
E.D. Mares, Relevant Logic: A Philosophical Interpretation (Cambridge Univeristy Press, Cambridge, 2004)
E.D. Mares, R. Goldblatt, An alternative semantics for quantified relevant logic. J. Symb. Logic 71(1), 163–187 (2006)
Y. Maruyama, Full lambek hyperdoctrine: categorical semantics for first-order substructural logics, in International Workshop on Logic, Language, Information, and Computation (Springer, 2013), pp. 211–225
A.M. Pitts. Categorical Logic, Technical report, University of Cambridge, Computer Laboratory (1995)
S. Read, Relevant Logic: A Philosophical Examination of Inference (Blackwell, Oxford, 1988)
G. Restall, Negation in relevant logics (how I stopped worrying and learned to love the Routley star), in What is Negation?, ed. by D.M. Gabbay, H. Wansing (Kluwer Academic Publishers, 1999), pp. 53–76
R. Routley, V. Routley, The semantics of first degree entailment. Noús 335–359 (1972)
R.A. Seely, Hyperdoctrines, natural deduction and the Beck condition. Math. Logic Quart. 29(10), 505–542 (1983)
J. Slaney, A general logic. Australasian J. Philos. 68(1), 74–88 (1990)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: Soundness for Stratified Models
Lemma 22
(HH—Horizontal Heredity) If \(X,s\vDash \phi \) and \(s\le t\), then \(X,t\vDash \phi \).
Proof
By a straightforward induction on \(\phi \).
Lemma 23
\(t\mathord {\downarrow }^Y_Xu\mathord {\downarrow }^Y_X\le (tu)\mathord {\downarrow }^Y_X\).
Proof
By fiddling with arrows; the discussion preceding Lemma 1 in [7] has hints.
Lemma 24
(Symmetry)  iff
iff  .
.
Proof
By induction on \(\phi \). The base case follows from SM2; and the conjunction case is trivial. In each of the remaining cases, the ‘if’ direction is the same as that ‘only if’ direction, so we deal only with the former.
For the negation case, let  . Then \(X,p^*\vDash \psi (b)\) for some
. Then \(X,p^*\vDash \psi (b)\) for some  . By SM5, for some u with
. By SM5, for some u with  ,
,  . Thus
. Thus  . So by HH,
. So by HH,  . But by SM3,
. But by SM3,  . Thus by IH,
. Thus by IH,  . So
. So  .
.
For conditionals, first suppose  . Let \(X,u\vDash \phi _1(b)\). Then by IH,
. Let \(X,u\vDash \phi _1(b)\). Then by IH,  . Thus
. Thus  . By SM4,
. By SM4,  . Thus by HH,
. Thus by HH,  as well. So
as well. So  .
.
Suppose instead that  . Let \(X,u\vDash \phi _1\). Then
. Let \(X,u\vDash \phi _1\). Then  . Thus, by IH,
. Thus, by IH,  . But by SM4 and the fact that
. But by SM4 and the fact that  is a closure operator,
is a closure operator,  . So by HH
. So by HH  . So
. So  .
.
Finally we deal with universals. Suppose  . Then
. Then  for some \(Y\supsetneq X\) and \(y\in Y-X\). Thus by SM17,
for some \(Y\supsetneq X\) and \(y\in Y-X\). Thus by SM17,  .The inductive hypothesis then gives that
.The inductive hypothesis then gives that  . So by SM17 again,
. So by SM17 again,  . Thus
. Thus  .
.
Lemma 25
(DH—Downward Heredity) If \(X\subseteq Y\), and \(\phi \in \mathscr {L}_X\) then \(Y,t\vDash \phi \) iff \(X,t\mathord {\downarrow }^Y_X\vDash \phi \).
Proof
By induction on \(\phi \). Most cases are straightforward. The universal case is not.
Suppose \(Y,t\vDash \forall v\psi (v)\). Then \(Z,t\mathord {\uparrow }^Z_Y\vDash \psi (z)\) for some \(Z\supsetneq Y\) and \(z\in Z-Y\). Let \(W=X\cup (Z-Y)\). Notice that \(Y\cap W=X\). So by SM9, \(t\mathord {\uparrow }^Z_Y\mathord {\downarrow }^Z_W=t\mathord {\downarrow }^Y_X\mathord {\uparrow }^W_X\). But by IH, \(W,t\mathord {\uparrow }^Z_Y\mathord {\downarrow }^Z_W\vDash \psi (z)\). So \(W,t\mathord {\downarrow }^Y_X\mathord {\uparrow }^W_X\vDash \psi (z)\). Thus \(X,t\mathord {\downarrow }^Y_X\vDash \forall v\psi (v)\).
Now suppose \(X,t\mathord {\downarrow }^Y_X\vDash \forall k\psi (k)\). Then \(Z,t\mathord {\downarrow }^Y_X\mathord {\uparrow }^Z_X\vDash \psi (z)\) for some \(Z\supsetneq X\) and \(z\in Z-X\). At this point the proof splits into two cases.
Case 1: Suppose \(z\not \in Y\). Notice that \(t\mathord {\downarrow }^Y_X\mathord {\uparrow }^{Z\cup Y}_X\mathord {\downarrow }^{Z\cup Y}_Z=t\mathord {\downarrow }^Y_X\mathord {\uparrow }^Z_X\mathord {\uparrow }^{Z\cup Y}_Z\mathord {\downarrow }^{Z\cup Y}_Z=t\mathord {\downarrow }^Y_X\mathord {\uparrow }^Z_X\). So since \(Z,t\mathord {\downarrow }^Y_X\mathord {\uparrow }^Z_X\vDash \psi (z)\), IH gives that \(Z\cup Y,t\mathord {\downarrow }^Y_X\mathord {\uparrow }^{Z\cup Y}_X\vDash \psi (z)\) as well. But \(t\mathord {\downarrow }^Y_X\mathord {\uparrow }^{Z\cup Y}_X=t\mathord {\downarrow }^Y_X\mathord {\uparrow }^Y_X\mathord {\uparrow }^{Y\cup Z}_Y\le t\mathord {\uparrow }_Y^{Z\cup Y}\). So by HH, \(Z\cup Y,t\mathord {\uparrow }^{Z\cup Y}_Y\vDash \psi (z)\). Since \(z\not \in Y\), this shows that \(Y,t\vDash \forall k\psi (k)\).
Case 2: suppose \(z\in Y\). Choose \(w\not \in Z\cup Y\). Let \(X^+=X\cup \{w\}\), \(Y^+=Y\cup \{w\}\) and \(Z^+=Z\cup \{w\}\). By a similar argument as before, \(t\mathord {\downarrow }^Y_X\mathord {\uparrow }_X^{Z^+\cup Y^+}\mathord {\downarrow }^{Z^+\cup Y^+}_Z=t\mathord {\downarrow }^Y_X\mathord {\uparrow }_X^Z\). Since \(Z,t\mathord {\downarrow }^Y_X\mathord {\uparrow }_X^Z\vDash \psi (z)\), by IH, \(Z^+\cup Y^+,t\mathord {\downarrow }^Y_X\mathord {\uparrow }_X^{Z^+\cup Y^+}\vDash \psi (z)\). So since  , HH gives
, HH gives  . Thus by symmetry
. Thus by symmetry  . So since \(w\in X^+\), IH then gives
. So since \(w\in X^+\), IH then gives  .
.
Finally, notice that since \(z\in (Z^+\cup Y^+)-X^+\), we have that

Thus by HH, \(X^+,t\mathord {\downarrow }^Y_X\mathord {\uparrow }_X^{X^+}\vDash \psi (w)\). But since \(w\not \in Y\), we now find ourselves (after swapping \(X^+\) for Z and w for z) in exactly the same situation as in the previous case. Thus by the argument given there, \(Y,t\vDash \forall v\psi (v)\).
Corollary 2
If \(Y,s\mathord {\uparrow }^Y_X\vDash \phi (y)\) for some \(Y\supsetneq X\) and \(y\in Y-X\), then \(X,s\vDash \phi (x)\) for all \(x\in X\).
Proof
Let \(x\in \mathrm {Dom}_X\). Since  , HH gives that
, HH gives that  . Thus by symmetry
. Thus by symmetry  . So by DH,
. So by DH,  . Since \(y\in Y-X\), SM18 gives that
. Since \(y\in Y-X\), SM18 gives that  . So by HH, \(X,s\vDash \phi (x)\).
. So by HH, \(X,s\vDash \phi (x)\).
Theorem 4
If \(\phi \in \mathrm {RWQ}\), then \(\mathbf {Str}\vDash \phi \).
Proof
By a straightforward induction on the proof of \(\phi \).
Appendix 2: Completeness
We begin with some definitions:
-
Write
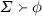 when there is a sequence \(\phi _1,\phi _2,\dots ,\phi _n\) such that \(\phi _n=\phi \) and for all \(1\le i\le n\), either
when there is a sequence \(\phi _1,\phi _2,\dots ,\phi _n\) such that \(\phi _n=\phi \) and for all \(1\le i\le n\), either-
\(\phi _i\in \varSigma \); or
-
For some \(j<i\) and \(k<i\), \(\phi _i=\phi _j\wedge \phi _k\); or
-
For some \(j<i\), \(\phi _j\rightarrow \phi _i\in \mathrm {RWQ}\).
-
-
Write
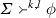 when there is a sequence \(\phi _1,\phi _2,\dots ,\phi _n\) such that \(\phi _n=\phi \) and for all \(1\le i\le n\), either
when there is a sequence \(\phi _1,\phi _2,\dots ,\phi _n\) such that \(\phi _n=\phi \) and for all \(1\le i\le n\), either-
\(\phi _i\in \varSigma \); or
-
For some \(j<i\) and \(k<i\), \(\phi _i=\phi _j\wedge \phi _k\); or
-
For some \(j<i\), \(\phi _j\rightarrow \phi _i\in \mathrm {RWQ}\); or
-
For some \(j<i\), \(\phi _i=\phi _j(k/l)\); or
-
For some \(j<i\), \(\phi _i=\phi _j(l/k)\).
-
-
Write \(\phi (x//y)\) for the result of replacing every occurrence of x in \(\phi \) with y.
-
Write \(c(\varSigma )\) for
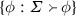 and \(c_X(\varSigma )\) for
and \(c_X(\varSigma )\) for 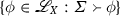 .
. -
Write \(c^{k,l}(\varSigma )\) for
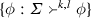 and write \(c_X^{k,l}(\varSigma )\) for
and write \(c_X^{k,l}(\varSigma )\) for 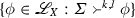 .
. -
Say \(\varSigma \) is an X-theory when \(\varSigma \subseteq \mathscr {L}_X\) and for all \(\phi \in \mathscr {L}_X\),
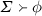 only if \(\phi \in \varSigma \).
only if \(\phi \in \varSigma \). -
Say \(\varSigma \) is an \(X^{k,l}\)-theory when \(\varSigma \subseteq \mathscr {L}_X\) and for all \(\phi \in \mathscr {L}_X\),
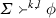 only if \(\phi \in \varSigma \).
only if \(\phi \in \varSigma \). -
We write \(\mathrm {RWQ}_X\) for \(\mathrm {RWQ}\cap \mathscr {L}_X\).
-
Say \(\varSigma \) is X-normal when \(\mathrm {RWQ}_X\subseteq \varSigma \).
-
Say \(\varSigma \) is prime when \(\alpha \vee \beta \in \varSigma \) only if \(\alpha \in \varSigma \) or \(\beta \in \varSigma \).
-
Say \(\varSigma \) is closed under disjunction when \(\alpha \vee \beta \in \varSigma \) whenever \(\alpha \in \varSigma \) and \(\beta \in \varSigma \).
Lemma 26
(Deduction Lemma) If  , then \(\alpha \rightarrow \beta \in \mathrm {RWQ}\).
, then \(\alpha \rightarrow \beta \in \mathrm {RWQ}\).
Lemma 27
If  , k not free in \(\varSigma \) but free for x in \(\phi (k )\), then
, k not free in \(\varSigma \) but free for x in \(\phi (k )\), then  .
.
Lemma 28
(Lindenbaum) Suppose \(\varDelta \) is closed under disjunction, \(\varGamma \) is an X-(or \(X^{k,l}\)-)theory, and \(\varGamma \cap \varDelta =\emptyset \). Then there is a prime X-(or \(X^{k,l}\)-)theory \(\varGamma '\supset \varGamma \) such that \(\varGamma '\cap \varDelta =\emptyset \).
Lemma 29
If \(\varGamma \) is a theory and \(\{\varGamma _i\}_{i\in I}\) is the set of all prime theories that contain \(\varGamma \), then \(\varGamma =\cap _{i\in I}\varGamma _i\)
Lemma 30
For each X, \(\mathrm {RWQ}_X\) is a prime X-theory.
For proofs of Lemmas 26–30, see [13]. We also need the following facts about \(\mathrm {RWQ}\):
-
Fact 1
\((\phi \rightarrow (\psi \rightarrow \rho ))\rightarrow (\psi \rightarrow (\phi \rightarrow \rho ))\in \mathrm {RWQ}\)
-
Fact 2
\(\phi \rightarrow (\psi \rightarrow ((\phi \rightarrow (\psi \rightarrow \rho ))\rightarrow \rho ))\in \mathrm {RWQ}\)
-
Fact 3
\(\phi \rightarrow \lnot \lnot \phi \in \mathrm {RWQ}\).
-
Fact 4
\(\phi \rightarrow (\phi \vee \psi )\in \mathrm {RWQ}\).
-
Fact 5
\(\lnot (\phi \wedge \psi )\rightarrow (\lnot \phi \vee \lnot \psi )\in \mathrm {RWQ}\).
-
Fact 6
\((\phi \rightarrow \psi )\rightarrow (\lnot \psi \rightarrow \lnot \phi )\in \mathrm {RWQ}\).
Finally, we will have need of the following two lemmas whose proofs we leave to the reader:
Lemma 31
 iff
iff  iff \(\rho (l//k)\rightarrow \psi (l//k)\in \mathrm {RWQ}\)
iff \(\rho (l//k)\rightarrow \psi (l//k)\in \mathrm {RWQ}\)
Lemma 32
If  and
and  , then
, then  .
.
Definition 11
For finite \(X\subseteq \mathrm {Var}\) we define \(\mathbf {M}(X)\) as \(\langle T_X,\cdot _X,\mathrm {RWQ}_X,\subseteq ,\varPi _X,*_X,X,I_X\rangle \), where \(T_X\) is the set of X-theories, \(t\cdot _X u=\{\psi :\phi \rightarrow \psi \in t\text { and }\phi \in u\}\), \(\varPi _X\) is the set of prime X-theories, \(t^{*_X}=\{\phi \in \mathscr {L}_X:\lnot \phi \not \in t\}\), and \(I_X(t)(P)=\{\overline{x}:P\overline{x}\in t\}\).
Lemma 33
\(\langle T_X,\cdot _X\rangle \) is a commutative monoid for which \(\mathrm {RWQ}_X\) serves as an identity element. Further, if a and b are in \(\varPi _X\) and \(ta\subseteq b\), then \(tb^{*_X}\subseteq a^{*_X}\), and \((a^{*_X})^{*_X}=a\).
Proof
By a straightforward application of the facts and definitions above.
Lemma 34
If \(p\in \varPi _X\), then \(p^{*_X}\in \varPi _X\).
Proof
We first prove that \(p^{*_X}\) is an X-theory. So let \(\phi \in \mathscr {L}_X\) and  . We show by induction on the length of the proof witnessing
. We show by induction on the length of the proof witnessing  that \(\phi \in p^{*_X}\). Let \(\psi _1,\dots ,\psi _i=\phi \) be such a proof. If \(i=1\), then \(\psi _1=\phi \in p^{*_X}\), so we are done. Now suppose \(i>1\). Clearly if \(\psi _i\in p^{*_X}\) we are done.
that \(\phi \in p^{*_X}\). Let \(\psi _1,\dots ,\psi _i=\phi \) be such a proof. If \(i=1\), then \(\psi _1=\phi \in p^{*_X}\), so we are done. Now suppose \(i>1\). Clearly if \(\psi _i\in p^{*_X}\) we are done.
Next suppose for some \(j<i\) and \(k<i\), \(\phi =\psi _j\wedge \phi _k\). Then by IH, \(\psi _j\in p^{*_X}\) and \(\psi _k\in p^{*_X}\). So \(\lnot \psi _j\) and \(\lnot \psi _k\) are not in p. So since p is prime, \(\lnot \psi _j\vee \lnot \psi _k\) is not in p. Since p is a theory, it follows by Fact 5 that \(\lnot (\psi _j\wedge \psi _k)\not \in p\). So \(\psi _j\wedge \psi _k\in p^{*_X}\) as required.
Finally, suppose for some \(j<i\), \(\psi _j\rightarrow \phi \in \mathrm {RWQ}\). Then by inductive hypothesis, \(\psi _j\in p^{*_X}\). So \(\lnot \psi _j\not \in p\). Since \(\psi _j\rightarrow \phi \in \mathrm {RWQ}\), Fact 6 gives that \(\lnot \phi \rightarrow \lnot \psi _j\in \mathrm {RWQ}\). Thus since p is a theory and \(\lnot \psi _j\not \in p\), \(\lnot \phi \not \in p\). Thus \(\phi \in p^{*_X}\) as required.
Now we show that \(p^{*_X}\) is prime. So, suppose \(\phi \vee \psi \in p^{*_X}\) but that neither \(\phi \) nor \(\psi \) is in \(p^{*_X}\). Then \(\lnot (\phi \vee \psi )\not \in p\) but \(\lnot \phi \in p\) and \(\lnot \psi \in p\). Since p is a theory, it follows that \(\lnot \phi \wedge \lnot \psi \in p\). So by Fact 3, \(\lnot \lnot (\lnot \phi \wedge \lnot \psi )\in p\). But by the definition of ‘\(\vee \)’, \(\lnot \lnot (\lnot \phi \wedge \lnot \psi )\in p\) gives that \(\lnot (\phi \vee \psi )\in p\), contradicting \(\lnot (\phi \vee \psi )\not \in p\). Thus, either \(\phi \in p^{*_X}\) or \(\psi \in p^{*_X}\), so \(p^{*_X}\) is prime.
Lemma 35
For all a and b in \(T_X\), if \(p\in \varPi _X\) and \(a b\subseteq p\) then there are \(q_1\) and \(q_2\) in \(\varPi _X\) so that \(a\subseteq q_1\) and \(q_1 b\subseteq p\), and \(b\subseteq q_2\) and \(a q_2\subseteq p\).
Proof Sketch. The result follows from several straightforward applications of the Lindenbaum lemma, so I leave some of the details to the reader. To begin, let \(\theta _1=\{\phi : c_X(\phi )b\not \subseteq p\}\) and let \(\theta _2=\{\phi : ac_X(\phi )\not \subseteq p\}\). I claim both \(\theta _1\) and \(\theta _2\) are closed under disjunction. To see this for \(\theta _1\), suppose \(\phi _1\) and \(\phi _2\) are in \(\theta _1\). Then \(c_X(\phi _1)b\not \subseteq p\) and \(c_X(\phi _2)b\not \subseteq p\). So there are \(\beta _1\), \(\beta _2\), \(\psi _1\), and \(\psi _2\) so that both for \(i=1\) and \(i=2\),  , \(\beta _i\in b\), and \(\psi _i\not \in p\). By fiddling, it follows from this that
, \(\beta _i\in b\), and \(\psi _i\not \in p\). By fiddling, it follows from this that  . But since b is a theory, \(\beta _1\wedge \beta _2\in b\), and since p is prime, \(\psi _1\vee \psi _2\not \in p\). Thus \(c_X(\phi _1\vee \phi _2)b\not \subseteq p\), so \(\phi _1\vee \phi _2\in \theta _1\).
. But since b is a theory, \(\beta _1\wedge \beta _2\in b\), and since p is prime, \(\psi _1\vee \psi _2\not \in p\). Thus \(c_X(\phi _1\vee \phi _2)b\not \subseteq p\), so \(\phi _1\vee \phi _2\in \theta _1\).
On the other hand, suppose \(\phi _1\) and \(\phi _2\) are in \(\theta _2\). Then \(ac_X(\phi _1)\not \subseteq p\) and \(ac_X(\phi _2)\not \subseteq p\). So there are \(\alpha _1\), \(\alpha _2\), \(\psi _1\), and \(\psi _2\) so both for \(i=1\) and \(i=2\),  , \(\alpha _i\rightarrow \psi _i\in a\), and \(\psi _i\not \in p\). By further fiddling, it follows from this that
, \(\alpha _i\rightarrow \psi _i\in a\), and \(\psi _i\not \in p\). By further fiddling, it follows from this that  and \((\alpha _1\vee \alpha _2)\rightarrow (\psi _1\vee \psi _2)\in a\) and \(\psi _1\vee \psi _2\not \in p\). So \(\phi _1\vee \phi _2\in \theta _2\).
and \((\alpha _1\vee \alpha _2)\rightarrow (\psi _1\vee \psi _2)\in a\) and \(\psi _1\vee \psi _2\not \in p\). So \(\phi _1\vee \phi _2\in \theta _2\).
Since \(ab\subseteq p\), it’s also clear that \(a\cap \theta _1=\emptyset \) and \(b\cap \theta _2=\emptyset \). So by the Lindenbaum Lemma, there are prime X-theories \(q_1\supseteq a\) with \(q_1\cap \theta _1=\emptyset \) and \(q_2\supseteq b\) with \(q_2\cap \theta _2=\emptyset \). It follows that \(q_1\) and \(q_2\) have the features we require.
Theorem 5
\(\langle T_X,\cdot _X,\mathrm {RWQ}_X,\subseteq ,\varPi _X,*_X,X,I_X\rangle \) is a z-model for each finite set of variables X.
Proof
Immediate from the definitions and Lemmas 33–35.
Lemma 36
\(c^{a,b}_X\) is a closure operator; for all t, \(c^{a,b}_X(t)\) is symmetric in a and b; for all prime X-theories p, \(c^{a,b}_X(p)\) is also prime, and if t is already symmetric in a and b, then \(c^{a,b}_X(t)=t\).
Proof
Essentially immediate from the definitions.
Lemma 37
\(c^{a,b}_X((c^{a,b}_X(t))^{*_X})=(c^{a,b}_X(t))^{*_X}\).
Proof
It suffices to show that \(c^{a,b}_X((c^{a,b}_X(t))^{*_X})\subseteq (c^{a,b}_X(t))^{*_X}\), the converse containment being a corollary of the previous lemma.
Since \((c^{a,b}_X(t))^{*_X}\) is obviously an X-theory all we need to show is that it’s an \(X^{a,b}\)-theory. So let \(\phi (a)\in (c^{a,b}_X(t))^{*_X}\). Then \(\lnot \phi (a)\not \in c^{a,b}_X(t)\). Thus since \(c^{a,b}_X(t)\) is an \(X^{a,b}\)-theory, \(\lnot \phi (b)\not \in c^{a,b}_X(t)\). So \(\phi (b)\in (c^{a,b}_X(t))^{*_X}\).
Lemma 38
\(c^{a,b}_X(tu)\subseteq c^{a,b}_X(t)c^{a,b}_X(u)\).
Proof
Let \(\phi \in c^{a,b}_X(tu)\). Then  . Thus, for some \(\psi \in tu\),
. Thus, for some \(\psi \in tu\),  . So there is a \(\rho \in u\subseteq c^{a,b}_X(u)\) with \(\rho \rightarrow \psi \in t\subseteq c^{a,b}_X(t)\). Thus \(\psi \in c^{a,b}_X(t)c^{a,b}_X(u)\). So since \(c^{a,b}_X(t)c^{a,b}_X(u)\) is an \(X^{a,b}\)-theory and
. So there is a \(\rho \in u\subseteq c^{a,b}_X(u)\) with \(\rho \rightarrow \psi \in t\subseteq c^{a,b}_X(t)\). Thus \(\psi \in c^{a,b}_X(t)c^{a,b}_X(u)\). So since \(c^{a,b}_X(t)c^{a,b}_X(u)\) is an \(X^{a,b}\)-theory and  , it follows that \(\phi \in c^{a,b}_X(t)c^{a,b}_X(u)\) as required.
, it follows that \(\phi \in c^{a,b}_X(t)c^{a,b}_X(u)\) as required.
Lemma 39
\(c^{a,b}_X(t)c^{a,b}_X(u)\subseteq c^{a,b}_X(t)u\).
Proof
Let \(\phi \in c^{a,b}_X(t)c^{a,b}_X(t)\). Then there is a \(\psi \in c^{a,b}_X(u)\) with \(\psi \rightarrow \phi \in c^{a,b}_X(t)\). Since \(\psi \in c^{a,b}_X(u)\), there is a \(\rho \in u\) with  . Thus by Lemma 31,
. Thus by Lemma 31,  . So since
. So since  , it follows by Lemma 11 that
, it follows by Lemma 11 that  . Thus \(\rho \rightarrow \phi \in c^{a,b}_X(t)\). So \(\phi \in c^{a,b}_X(t)u\).
. Thus \(\rho \rightarrow \phi \in c^{a,b}_X(t)\). So \(\phi \in c^{a,b}_X(t)u\).
Lemma 40
If \( c^{a,b}_X(s)\subseteq p\in \varPi _X\), then there is a t with \( c^{a,b}_X(s)\le c^{a,b}_X(t)\le p\) and \(c^{a,b}_X(t)\in \varPi _X\).
Proof
This is a straightforward application of the Lindenbaum Lemma for \(X^{a,b}\)-theories, so left to the reader.
Definition 12
For finite sets of variables \(X\subseteq Y\), we let \(t\mathord {\Downarrow }^Y_X=t\cap \mathscr {L}_X\) and \(t\mathord {\Uparrow }_X^Y=c_Y(t)\)
Lemma 41
\(\mathord {\Downarrow }\) and \(\mathord {\Uparrow }\) are monotonic; \(t\mathord {\Downarrow }^Z_Y\mathord {\Downarrow }^Y_X=t\mathord {\Downarrow }^Z_X\); \(t\mathord {\Uparrow }^Z_Y\mathord {\Uparrow }^Y_X=t\mathord {\Uparrow }^Z_X\); \(\mathrm {RWQ}_X\mathord {\Uparrow }_X^Y=\mathrm {RWQ}_Y\); \(t\mathord {\Downarrow }_X^Y\mathord {\Uparrow }^Y_X\subseteq t\); and \(t\mathord {\Uparrow }_X^Y\mathord {\Downarrow }^Y_X=t\)
Proof
Essentially immediate from definitions.
Lemma 42
\((t^{*_Y})\mathord {\Downarrow }^Y_X=(t\mathord {\Downarrow }^Y_X)^{*_X}\).
Proof
\(\phi \in (t^{*_Y})\mathord {\Downarrow }^Y_X\) iff \(\phi \in t^{*_Y}\cap \mathscr {L}_X\) iff \(\phi \in \mathscr {L}_X\) and \(\lnot \phi \not \in t\) iff \(\lnot \phi \not \in t\cap \mathscr {L}_X\) iff \(\phi \in (t\mathord {\Downarrow }^Y_X)^{*_X}\).
Lemma 43
\(\varPi _Y\mathord {\Downarrow }^Y_X=\varPi _X\).
Proof
We leave showing \(\varPi _Y\mathord {\Downarrow }^Y_X\subseteq \varPi _X\) to the reader. For the converse, let \(p\in \varPi _X\) and let \(\theta =\mathscr {L}_X-p\). Since p is prime, \(\theta \) is closed under disjunctions and clearly \(c_Y(p)\) is a Y-theory that does not intersect \(\theta \). Thus, by the Lindenbaum Lemma applied to Y-theories, there is a prime Y-theory q with \(p\subseteq c_Y(p)\subseteq q\) and \(q\cap \theta =\emptyset \). It follows that \(q\mathord {\Downarrow }^Y_X=p\). So \(\varPi _Y\mathord {\Downarrow }^Y_X\supseteq \varPi _X\).
Lemma 44
\((t^{*_X})\mathord {\Uparrow }^Y_X=(t\mathord {\Uparrow }^Y_X)^{*_Y}\) and \((ts)\mathord {\Uparrow }^Y_X=t\mathord {\Uparrow }^Y_Xs\mathord {\Uparrow }^Y_X\).
Proof
For the first of these, let \(\phi \in (t^{*_X})\mathord {\Uparrow }^Y_X\). Then  for some \(\tau _X\in t^{*_X}\). Since \(\tau _X\in t^{*_X}\), \(\lnot \tau \not \in t\). Thus
for some \(\tau _X\in t^{*_X}\). Since \(\tau _X\in t^{*_X}\), \(\lnot \tau \not \in t\). Thus  . So \(\lnot \tau \not \in t\mathord {\Uparrow }^Y_X\). Thus \(\tau \in (t\mathord {\Uparrow }^Y_X)^{*_Y}\), so since \((t\mathord {\Uparrow }^Y_X)^{*_Y}\) is a theory, \(\phi \in (t\mathord {\Uparrow }^Y_X)^{*_Y}\) as well.
. So \(\lnot \tau \not \in t\mathord {\Uparrow }^Y_X\). Thus \(\tau \in (t\mathord {\Uparrow }^Y_X)^{*_Y}\), so since \((t\mathord {\Uparrow }^Y_X)^{*_Y}\) is a theory, \(\phi \in (t\mathord {\Uparrow }^Y_X)^{*_Y}\) as well.
For the second, first note that since \(t\subseteq t\mathord {\Uparrow }^Y_X\) and \(s\subseteq s\mathord {\Uparrow }^Y_X\), the left-to-right containment is obvious. For the other direction, let \(\phi \in t\mathord {\Uparrow }^Y_X s\mathord {\Uparrow }^Y_X\). Then there is \(\psi \in s\mathord {\Uparrow }^Y_X=c_Y(s)\) with \(\psi \rightarrow \phi \in t\mathord {\Uparrow }^Y_X=c_Y(t)\). Since \(\psi \in c_Y(s)\), there is \(\sigma \in s\) with  . Thus by the Deduction Lemma, \(\sigma \rightarrow \psi \in \mathrm {RWQ}\). Thus, since \(\psi \rightarrow \phi \in t\), \(\sigma \rightarrow \phi \in t\) as well. So there is a \(\tau \in t\) with
. Thus by the Deduction Lemma, \(\sigma \rightarrow \psi \in \mathrm {RWQ}\). Thus, since \(\psi \rightarrow \phi \in t\), \(\sigma \rightarrow \phi \in t\) as well. So there is a \(\tau \in t\) with  and thus by the Deduction Lemma, \(\tau \rightarrow (\sigma \rightarrow \phi )\in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). Then by R3, \(\forall y_1\dots \forall y_n(\tau \rightarrow (\sigma \rightarrow \phi ))\in \mathrm {RWQ}\). So since \(\tau \in t\subseteq \mathscr {L}_X\) and \(\sigma \in s\subseteq \mathscr {L}_X\), A11 and a bit of fiddling give that \(\tau \rightarrow (\sigma \rightarrow \forall y_1\dots \forall y_n\phi )\in \mathrm {RWQ}\). Thus since \(\tau \in t\), \(\sigma \rightarrow \forall y_1\dots \forall y_n\phi \in t\). So since \(\sigma \in s\), \(\forall y_1\dots \forall y_n\phi \in ts\). Thus \(\phi \in (ts)\mathord {\Uparrow }^Y_X\).
and thus by the Deduction Lemma, \(\tau \rightarrow (\sigma \rightarrow \phi )\in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). Then by R3, \(\forall y_1\dots \forall y_n(\tau \rightarrow (\sigma \rightarrow \phi ))\in \mathrm {RWQ}\). So since \(\tau \in t\subseteq \mathscr {L}_X\) and \(\sigma \in s\subseteq \mathscr {L}_X\), A11 and a bit of fiddling give that \(\tau \rightarrow (\sigma \rightarrow \forall y_1\dots \forall y_n\phi )\in \mathrm {RWQ}\). Thus since \(\tau \in t\), \(\sigma \rightarrow \forall y_1\dots \forall y_n\phi \in t\). So since \(\sigma \in s\), \(\forall y_1\dots \forall y_n\phi \in ts\). Thus \(\phi \in (ts)\mathord {\Uparrow }^Y_X\).
Lemma 45
\((tu\mathord {\Uparrow }^Y_X)\mathord {\Downarrow }^Y_X\subseteq t\mathord {\Downarrow }^Y_Xu\).
Proof
Let \(\phi \in (tu\mathord {\Uparrow }^Y_X)\mathord {\Downarrow }^Y_X\). Then \(\phi \in \mathscr {L}_X\) and there is a \(\psi \in u\mathord {\Uparrow }^Y_X\) with \(\psi \rightarrow \phi \in t\). Since \(\psi \in u\mathord {\Uparrow }^Y_X\), for some \(\rho \in u\),  . Thus \(\rho \rightarrow \psi \in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). Then using R3 and A11, we see that \(\rho \rightarrow \forall y_1\dots \forall y_n\psi \in \mathrm {RWQ}\). It follows that \(\forall y_1\dots \forall y_n\psi \in u\). But repeated applications of A10 and R1 give that \(\forall y_1\dots \forall y_n\psi \rightarrow \psi \in \mathrm {RWQ}\). So since \(\psi \rightarrow \phi \in t\), \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in t\) as well. But also \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in \mathscr {L}_X\). So \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in t\mathord {\Downarrow }^Y_X\), so \(\phi \in t\mathord {\Downarrow }^Y_Xu\).
. Thus \(\rho \rightarrow \psi \in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). Then using R3 and A11, we see that \(\rho \rightarrow \forall y_1\dots \forall y_n\psi \in \mathrm {RWQ}\). It follows that \(\forall y_1\dots \forall y_n\psi \in u\). But repeated applications of A10 and R1 give that \(\forall y_1\dots \forall y_n\psi \rightarrow \psi \in \mathrm {RWQ}\). So since \(\psi \rightarrow \phi \in t\), \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in t\) as well. But also \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in \mathscr {L}_X\). So \(\forall y_1\rightarrow \forall y_n\psi \rightarrow \phi \in t\mathord {\Downarrow }^Y_X\), so \(\phi \in t\mathord {\Downarrow }^Y_Xu\).
Lemma 46
\(I_Y(t)(P)\cap \mathrm {Dom}^i_X=I_X(t\mathord {\Downarrow }^Y_X)(P)\).
Proof
Immediate from definitions.
Lemma 47
If \(t\mathord {\Downarrow }^Y_X\subseteq a\), then for some \(p\in \varPi _Y\), \(t\subseteq p\) and \(t\mathord {\Downarrow }^Y_X=a\).
Proof
Let \(s=c_Y(t\cup a)\) and let \(\theta =\mathscr {L}_X-a\) Clearly s is a Y-theory. I claim \(s\cap \theta =\emptyset \).
To see this, suppose \(\phi \in s\cap \theta \). Then  . So there is \(\tau \in t\) and \(\alpha \in a\) so that
. So there is \(\tau \in t\) and \(\alpha \in a\) so that  . Thus by the Deduction Lemma, \((\tau \wedge \alpha )\rightarrow \phi \in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). By fiddling, it’s clear then that \((\forall y_1\dots \forall y_n\tau \wedge \forall y_1\dots \forall y_n\alpha )\rightarrow \phi \in \mathrm {RWQ}\) as well. But \(\forall y_1\dots \forall y_n\tau \in t\mathord {\Downarrow }^Y_X\subseteq a\) and \(\forall y_1\dots \forall y_n\alpha \in a\). So \(\forall y_1\dots \forall y_n\tau \wedge \forall y_1\dots \forall y_n\alpha \in a\), from which it follows that \(\phi \in a\), which is impossible. So \(s\cap \theta =\emptyset \). Thus the Lindenbaum Lemma applied to Y-theories gives that there is a \(p\in \varPi _Y\) with \(s\subseteq p\) and \(p\cap \theta =\emptyset \). Since \(a\subseteq s\) and \(t\subseteq s\), \(a\subseteq p\) and \(t\subseteq p\). And since \(p\cap \theta =\emptyset \), \(p\subseteq a\), showing that p has the required features.
. Thus by the Deduction Lemma, \((\tau \wedge \alpha )\rightarrow \phi \in \mathrm {RWQ}\). Let \(Y-X=\{y_1,\dots ,y_n\}\). By fiddling, it’s clear then that \((\forall y_1\dots \forall y_n\tau \wedge \forall y_1\dots \forall y_n\alpha )\rightarrow \phi \in \mathrm {RWQ}\) as well. But \(\forall y_1\dots \forall y_n\tau \in t\mathord {\Downarrow }^Y_X\subseteq a\) and \(\forall y_1\dots \forall y_n\alpha \in a\). So \(\forall y_1\dots \forall y_n\tau \wedge \forall y_1\dots \forall y_n\alpha \in a\), from which it follows that \(\phi \in a\), which is impossible. So \(s\cap \theta =\emptyset \). Thus the Lindenbaum Lemma applied to Y-theories gives that there is a \(p\in \varPi _Y\) with \(s\subseteq p\) and \(p\cap \theta =\emptyset \). Since \(a\subseteq s\) and \(t\subseteq s\), \(a\subseteq p\) and \(t\subseteq p\). And since \(p\cap \theta =\emptyset \), \(p\subseteq a\), showing that p has the required features.
Lemma 48
If a and b are in X, then \(c^{a,b}_Y(t\mathord {\Uparrow }_X^Y)=c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\).
Proof
If \(\phi \in c^{a,b}_Y(t\mathord {\Uparrow }^Y_X)\), then \(\phi \in \mathscr {L}_Y\) and  . Thus,
. Thus,  for some \(\tau _Y\in t\mathord {\Uparrow }^Y_X\). So by Lemma 31,
for some \(\tau _Y\in t\mathord {\Uparrow }^Y_X\). So by Lemma 31,  . Since \(\tau _Y\in t\mathord {\Uparrow }^Y_X\),
. Since \(\tau _Y\in t\mathord {\Uparrow }^Y_X\),  for some \(\tau _X\in t\). So
for some \(\tau _X\in t\). So  . Thus, by fiddling,
. Thus, by fiddling,  . Let \(Y-X=\{y_1,\dots ,y_n\}\). Then by repeated application of R3,
. Let \(Y-X=\{y_1,\dots ,y_n\}\). Then by repeated application of R3,  . So by fiddling,
. So by fiddling,  . It follows that \(\forall y_1\dots \forall y_n\phi \in c^{a,b}_X(t)\). So \(\phi \in c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\). Thus \(c^{a,b}_Y(t\mathord {\Uparrow }_X^Y)\subseteq c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\).
. It follows that \(\forall y_1\dots \forall y_n\phi \in c^{a,b}_X(t)\). So \(\phi \in c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\). Thus \(c^{a,b}_Y(t\mathord {\Uparrow }_X^Y)\subseteq c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\).
Now let \(\phi \in c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\). Then  for some \(\tau \in c^{a,b}_X(t)\). Since \(\tau \in c^{a,b}_X(t)\),
for some \(\tau \in c^{a,b}_X(t)\). Since \(\tau \in c^{a,b}_X(t)\),  for some \(\tau '\in t\). Since \(\tau '\in t\), \(\tau '\in t\mathord {\Uparrow }^Y_X\). So since
for some \(\tau '\in t\). Since \(\tau '\in t\), \(\tau '\in t\mathord {\Uparrow }^Y_X\). So since  , \(\tau \in c^{a,b}_Y(t\mathord {\Uparrow }^Y_X)\). Finally, since
, \(\tau \in c^{a,b}_Y(t\mathord {\Uparrow }^Y_X)\). Finally, since  , this gives that \(\phi \in c^{a,b}_Y(t\mathord {\Uparrow }^Y_X)\). So \(c^{a,b}_Y(t\mathord {\Uparrow }_X^Y)\supseteq c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\), completing the proof.
, this gives that \(\phi \in c^{a,b}_Y(t\mathord {\Uparrow }^Y_X)\). So \(c^{a,b}_Y(t\mathord {\Uparrow }_X^Y)\supseteq c^{a,b}_X(t)\mathord {\Uparrow }^Y_X\), completing the proof.
Lemma 49
If \(a\in Y-X\) and \(b\in X\), then \( c^{b,a}_Y(t\mathord {\Uparrow }^Y_X)\mathord {\Downarrow }^Y_X\subseteq t\)
Proof
Let \(\phi \in c^{b,a}_Y(t\mathord {\Uparrow }^Y_X)\mathord {\Downarrow }^Y_X\). Then \(\phi \in \mathscr {L}_X\) and \(\phi \in c^{b,a}_Y(t\mathord {\Uparrow }^Y_X)\). So  , and thus
, and thus  for some \(\tau _y\in t\mathord {\Uparrow }^Y_X\). And since \(\tau _Y\in t\mathord {\Uparrow }^Y_X\),
for some \(\tau _y\in t\mathord {\Uparrow }^Y_X\). And since \(\tau _Y\in t\mathord {\Uparrow }^Y_X\),  for some \(\tau _X\in t\). It follows that
for some \(\tau _X\in t\). It follows that  . Thus by Lemma 31, \(\tau _X(a//b)\rightarrow \phi (a//b)\in \mathrm {RWQ}\). But since \(a\in Y-X\) and \(\tau _X\) and \(\phi \) are in \(\mathscr {L}_X\), a does not occur in \(\tau _X\) or in \(\phi \). So \(\tau _X(a//b)=\tau \) and \(\phi (a//b)=\phi \). So in fact \(\tau _X\rightarrow \phi \in \mathrm {RWQ}\). Thus since t is a theory and \(\tau _X\in t\), \(\phi \in t\) as well, as required.
. Thus by Lemma 31, \(\tau _X(a//b)\rightarrow \phi (a//b)\in \mathrm {RWQ}\). But since \(a\in Y-X\) and \(\tau _X\) and \(\phi \) are in \(\mathscr {L}_X\), a does not occur in \(\tau _X\) or in \(\phi \). So \(\tau _X(a//b)=\tau \) and \(\phi (a//b)=\phi \). So in fact \(\tau _X\rightarrow \phi \in \mathrm {RWQ}\). Thus since t is a theory and \(\tau _X\in t\), \(\phi \in t\) as well, as required.
Lemma 50
for all \(V\supseteq X\), \(t\mathord {\Uparrow }^V_X\mathord {\Downarrow }^V_W=t\mathord {\Downarrow }^X_Y\mathord {\Uparrow }^W_Y\), as long as \(X\cap W=Y\)
Proof
Let \(Y\cap Z=X\), \(W\supseteq Y\) and let \(\phi \in t\mathord {\Downarrow }^Y_X\mathord {\Uparrow }^Z_X\). Then \(\tau _X\rightarrow \phi \in \mathrm {RWQ}\) for some \(\tau _X\in t\mathord {\Downarrow }^Y_X=t\cap \mathscr {L}_X\). Since \(\tau _X\in t\), \(\tau _X\in t\mathord {\Uparrow }^W_Y\). But then since \(\mathscr {L}_X\subseteq \mathscr {L}_Z\), we also have that \(\tau _X\in \mathord {\Uparrow }^W_Y\mathord {\Downarrow }^W_Z\). So \(t\mathord {\Downarrow }^Y_X\mathord {\Uparrow }^Z_X\subseteq t\mathord {\Uparrow }^W_Y\mathord {\Downarrow }^W_Z\).
Now let \(\phi \in t\mathord {\Uparrow }_Y^W\mathord {\Downarrow }^W_Z=t\mathord {\Uparrow }_Y^W\cap \mathscr {L}_Z\). Then \(\tau _Y\rightarrow \phi \in \mathrm {RWQ}\) for some \(\tau _Y\in t\). Let \(Z-Y=\{z_1,\dots ,z_n\}\). Then by repeated application of R3, \(\forall z_1\dots \forall z_n(\tau _Y\rightarrow \phi )\in \mathrm {RWQ}\) as well. So by fiddling, \(\tau _Y\rightarrow \forall z_1\dots \forall z_n\phi \in \mathrm {RWQ}\). So since \(\tau _Y\in t\), clearly \(\forall z_1\dots \forall z_n\phi \in t\). But clearly \(\forall z_1\dots \forall z_n\phi \in \mathscr {L}_{Z\cap Y}=\mathscr {L}_X\). So in fact \(\forall z_1\dots \forall z_n\phi \in t\mathord {\Downarrow }^Y_X\), from which it follows that \(\phi \in t\mathord {\Downarrow }^Y_X\mathord {\Uparrow }_X^Z\).
Theorem 6
The data \(\mathbf {M}\), cb, \(\mathord {\Downarrow }\), \(\mathord {\Uparrow }\) define a stratified model.
Proof
Immediate from the above.
Lemma 51
If \(\phi \in \mathscr {L}_X\), then \(\mathbf {M},X,t\vDash \phi \) iff \(\phi \in t\).
Proof
By induction on \(\phi \). The cases for atoms and conjunctions are trivial. For the conditional case, first suppose that \(\phi \rightarrow \psi \in t\). Let \(\mathbf {M},X,u\vDash \phi \). Then by IH, \(\phi \in u\). So \(\psi \in tu\), and thus, again by IH, \(\mathbf {M},X,tu\vDash \psi \). Now suppose instead that \(\phi \rightarrow \psi \not \in t\). Let \(u=c_X(\phi )\). Clearly \(\phi \in u\). So by IH, \(\mathbf {M},X,u\vDash \phi \). Suppose \(\psi \in tu\). Then \(\rho \rightarrow \psi \in t\) for some \(\rho \in u\). But if \(\rho \in u\), then \(\phi \rightarrow \rho \in \mathrm {RWQ}\), and hence \(\phi \rightarrow \psi \in t\), which is a contradiction. So \(\psi \not \in tu\). Thus by IH, \(\mathbf {M},X,tu\not \vDash \psi \). So \(\mathbf {M},X,t\not \vDash \phi \rightarrow \psi \).
For the universal case, first suppose \(M,X,t\vDash \forall k\phi (k)\). Then there are \(Y\supsetneq X\) and \(y\in Y-X\) so that \(M,Y,t\mathord {\Uparrow }^Y_X\vDash \phi (y)\). So by IH, \(\phi (y)\in t\mathord {\Uparrow }^Y_X=c_Y(t)\). So \(t\vDash \phi (y)\). So for some \(\tau \in t\), \(\tau \rightarrow \phi (y)\in \mathrm {RWQ}\). Since \(\tau \in t\subseteq \mathscr {L}_X\) and \(y\in Y-X\), it follows by some fiddling that \(\tau \rightarrow \forall k\phi (k)\in \mathrm {RWQ}\) as well. So since \(\tau \in t\), \(\forall k\phi (k)\in t\) as well.
Finally, suppose \(\forall k\phi (k)\in t\). Let \(Y\supsetneq X\) and \(y\in Y\). Then \(\phi (y)\in c_Y(t)=t\mathord {\Uparrow }^Y_X\). So by IH, \(\mathbf {M},Y,t\mathord {\Uparrow }^Y_X\vDash \phi (y)\). It follows that \(\mathbf {M},X,t\vDash \forall k\phi (k)\) as required.
Theorem 7
If \(\mathbf {Str}\vDash \phi \), then \(\phi \in \mathrm {RWQ}\).
Proof
Let \(\phi \in \mathscr {L}_X\) and suppose \(\phi \not \in \mathrm {RWQ}\). Then \(\phi \not \in \mathrm {RWQ}_X\). So by Lemma 51, \(\mathbf {M},X,\mathrm {RWQ}_X\not \vDash \phi \). Thus \(\mathbf {Str}\not \vDash \phi \).
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Logan, S.A. (2021). Hyperdoctrines and the Ontology of Stratified Semantics. In: Fazio, D., Ledda, A., Paoli, F. (eds) Algebraic Perspectives on Substructural Logics. Trends in Logic, vol 55. Springer, Cham. https://doi.org/10.1007/978-3-030-52163-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-52163-9_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-52162-2
Online ISBN: 978-3-030-52163-9
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


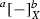 is a closure operator, we have that,
is a closure operator, we have that, 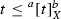 for all t; if
for all t; if 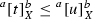 ; and
; and 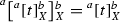 .
.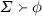 when there is a sequence
when there is a sequence 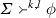 when there is a sequence
when there is a sequence 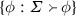 and
and 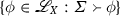 .
.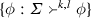 and write
and write 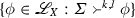 .
.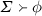 only if
only if 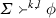 only if
only if