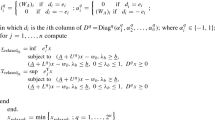Keywords

1 Introduction

An interval linear system of equations is normally referred to as a system \({\varvec{{A}}}x = {\varvec{{b}}}\), where \({\varvec{{A}}}\) is an interval matrix and \({\varvec{{b}}}\) is an interval vector, while x is a vector of variables. As the matrix and the right hand side vector information of the system is not precise, it is impossible to provide a solution x to the system without any appropriate meaning.

Some literature presented different types of solutions of the system \({\varvec{{A}}}x = {\varvec{{b}}}\) depending on the purposes of the solutions. These solution types include weak, strong, tolerance and control solutions whose names reflect well on their mathematical definitions. For example, “x is a weak solution to \({\varvec{{A}}}x = {\varvec{{b}}}\)” means that

$$ \exists A \in {\varvec{{A}}}, \exists b \in {\varvec{{b}}}\;\;\text {such that}\;\;Ax = b, $$

while “x is a strong solution to \({\varvec{{A}}}x = {\varvec{{b}}}\)” means that

$$ \forall A \in {\varvec{{A}}}, \forall b \in {\varvec{{b}}}\;\;\text {such that}\;\;Ax = b. $$

Beaumont presented in [1] an efficient method derived from the simplex algorithm to compute inner and outer inclusion of the weak (united) solution set. A full analysis of the solvability and the conditions for checking whether x is a particular solution type to the system \({\varvec{{A}}}x = {\varvec{{b}}}\) was also provided in the literature [2,3,4, 8,9,10,11,12].

The background on a tolerance solution arose from the crane construction problem in [8] and the input-output planning problem with inexact data in [11]. The characteristic of a tolerance solution x is to make \({\varvec{{A}}}x\) stay in the boundary of \({\varvec{{b}}}\). Shary [12] first motivated an idea of a control solution, which is the opposite case of a tolerance solution. In addition, Tian et al. developed in [13] a tolerance-control solution for the case when each row index of the system \({\varvec{{A}}}x = {\varvec{{b}}}\) performs either tolerance or control. Recently, Leela-apiradee, [6] , have provided its solution set in terms of level set.

Instead of the system \( {\varvec{{A}}}x = {\varvec{{b}}} \), the goal of this paper is to deal with a two-sided interval linear system. “Two-sided" means that the right hand side interval vector \({\varvec{{b}}} \) is substituted by the term \({\varvec{{B}}}y\). The paper then presents the tolerance and control solutions of a two-sided interval linear system together with their solvability conditions.

To lead to the main idea of the paper, let us first introduce some basic notation of an interval matrix and an interval vector that can be seen as a matrix and a vector of interval components as follows.

  • An \(m \times n\) interval matrix \({\varvec{{A}}}\) is defined by

    $$ {\varvec{{A}}} = \begin{pmatrix} \left[ \underline{a}_{11},\overline{a}_{11}\right] &{}\left[ \underline{a}_{12},\overline{a}_{12}\right] &{} \cdots &{}\left[ \underline{a}_{1n},\overline{a}_{1n}\right] \\ \left[ \underline{a}_{21},\overline{a}_{21}\right] &{}\left[ \underline{a}_{22},\overline{a}_{22}\right] &{} \cdots &{}\left[ \underline{a}_{2n},\overline{a}_{2n}\right] \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ \left[ \underline{a}_{m1},\overline{a}_{m1}\right] &{}\left[ \underline{a}_{m2},\overline{a}_{m2}\right] &{} \cdots &{}\left[ \underline{a}_{mn},\overline{a}_{mn}\right] \end{pmatrix}, $$

    where \(\underline{a}_{ij}\) and \(\overline{a}_{ij}\) are real numbers such that \(\underline{a}_{ij} \le \overline{a}_{ij}\) for each \(i\in \{1,2,\dots , m\}\) and \(j\in \{1,2,\dots , n\}\).

  • The interpretation of the interval matrix \({\varvec{{A}}}\) can be written as the set of matrices, that is,

    $$ {\varvec{{A}}} = \left[ \underline{A} , \overline{A}\right] =\left\{ A \in \mathbb {R}^{m\times n} : \underline{A} \le A \le \overline{A}\right\} , $$

    where

    $$ \underline{A} =\begin{pmatrix} \underline{a}_{11} &{} \underline{a}_{12} &{} \cdots &{}\underline{a}_{1n} \\ \underline{a}_{21} &{} \underline{a}_{22} &{} \cdots &{}\underline{a}_{2n} \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ \underline{a}_{m1} &{} \underline{a}_{m2} &{} \cdots &{}\underline{a}_{mn} \end{pmatrix}\;\;{and}\;\;\overline{A} = \begin{pmatrix} \overline{a}_{11} &{} \overline{a}_{12} &{} \cdots &{}\overline{a}_{1n} \\ \overline{a}_{21} &{} \overline{a}_{22} &{} \cdots &{}\overline{a}_{2n} \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ \overline{a}_{m1} &{} \overline{a}_{m2} &{} \cdots &{}\overline{a}_{mn} \end{pmatrix}. $$

    The ordering ‘\(\le \)’ between two matrices \(\underline{A}\) and \(\overline{A}\) is referred to componentwise inequality, i.e.,

    $$ \underline{A} \le \overline{A}\;\;\text {if and only if}\;\; \underline{a}_{ij}\le \overline{a}_{ij}\;\;\forall i\in \{1,2,\dots , m\}, \forall j\in \{1,2,\dots , n\}. $$

    Therefore, we note here that \(A\in {\varvec{{A}}}\) means \(\underline{A} \le A \le \overline{A}\).

Moreover, we can use the following notation to represent the interval matrix \({\varvec{{A}}}\).

$$\begin{aligned} {\varvec{{A}}}=\left[ \underline{A} , \overline{A}\right] = \left[ A_c - \varDelta _A, A_c+ \varDelta _A\right] , \end{aligned}$$
(1)

where \(A_c = \frac{1}{2} (\overline{A}+\underline{A})\) and \(\varDelta _A = \frac{1}{2} (\overline{A}-\underline{A})\).

Fiedler et al. proved in [2] that the lower and upper bounds of the interval vector \({\varvec{{A}}}x\), denoted by \(\underline{{\varvec{A}}x}\) and \(\overline{{\varvec{A}}x}\) for any \(x=(x_1, x_2, \dots , x_n)^T \in \mathbb {R}^n\), can be viewed by

$$\begin{aligned} {\varvec{{A}}}x =\left[ \underline{{\varvec{A}}x} , \overline{{\varvec{A}}x}\right] = \left[ A_c x -\varDelta _A |x|, \; A_c x + \varDelta _A |x|\,\right] , \end{aligned}$$
(2)

where |x| is defined as the absolute of vector x, i.e., \(|x| = (|x_1|, |x_2|, \dots , |x_n|)^T\).

Given \({\varvec{{B}}}\) be another interval matrix and y be another vector of variables. In the situation when we have the term \( {\varvec{{B}}}y\) on the right hand side instead of the vector \({\varvec{{b}}}\), the system “\({\varvec{{A}}}x = {\varvec{{b}}}\)” would become “\({\varvec{{A}}}x = {\varvec{{B}}}y\)”, which is called a two-sided interval linear system. The dimensions of x and y do not need to be the same but the number of rows of interval matrices \({\varvec{{A}}}\) and \({\varvec{{B}}}\) does. The definitions of weak, strong, tolerance control and tolerance-control solutions of \({\varvec{{A}}}x = {\varvec{{B}}}y\) would mathematically be defined in the same fashion as the case of \({\varvec{{A}}}x = {\varvec{{b}}}\).

In this paper, we focus on the tolerance, control and tolerance-control solutions of the system \({\varvec{{A}}}x = {\varvec{{B}}}y\). In Sect. 2 we give the definitions and their characterizations by equivalent conditions. Usually, two sets of quantities are equal when the left and the right quantities are the same. However, there is often a situation with imprecise information that one set of quantities is being controlled by the other. This means that if the two sets of quantities are not precise with having interval information, then one set of quantities must be subset of the other. Moreover, one set of the interval information could be more important to the system than the other. The other set of the interval information must follow the semantics of the context. This leads to the interpretation of tolerance and control solutions of a two-sided interval linear system discussed in Sect. 3. A couple of application examples are demonstrated in Sect. 4, which can be modeled by a two-sided interval linear system and a quadratic programming problem with two-sided interval linear constraints. The conclusion is addressed in the last section.

2 Tolerance and Control Solutions of Two-Sided Interval System of Linear Equations

To see how the two-sided interval systems are motivated, consider two systems of standard linear equations below:

$$\begin{aligned} Ax&= By, \end{aligned}$$
(3)
$$\begin{aligned} Ax - By&=0, \end{aligned}$$
(4)

where \(A\in \mathbb {R}^{m\times n}\), \(B\in \mathbb {R}^{m\times p}\), and m, n and p are positive integers. Any (x, y) in \(\mathbb {R}^{n} \times \mathbb {R}^{p}\) satisfying System (3) (or (4)) is called a solution of the system. It is clear that Systems (3) and (4) are algebraically equivalent. The set of solutions of (3) is the same as the set of solutions of (4). However, if the entries of coefficient matrices A and B in (3) and (4) are interval data, Systems (3) and (4) turn into

$$\begin{aligned} \varvec{A}x&= \varvec{B}y, \end{aligned}$$
(5)
$$\begin{aligned} \varvec{A}x - \varvec{B}y&= 0, \end{aligned}$$
(6)

respectively, where coefficient terms \(\varvec{A}\) and \(\varvec{B}\) in (5) and (6) are interval matrices as defined in the introduction section. System (6) could not be well-defined in general since the left-hand side may be represented as interval vector with non-zero width as a result of Moore’s standard interval arithmetic [7], while the right-hand side is a real zero vector with zero width. Therefore, we would not be able to move \(\varvec{B}y\) to the same side as \(\varvec{A}x\) of the equality as usual, when we deal with interval data. However, System (5) called a two-sided interval system of linear equations is well-defined since both sides of the equation are interval vectors. A solution \((x,y) \in \mathbb {R}^n \times \mathbb {R}^p\) to System (5) is not as simple as the case of standard matrices A and B, but it comes with its semantics.

In [2], Fiedler et al. defined tolerance and control solutions to an interval linear system \({\varvec{{A}}}x = {\varvec{{b}}}\). Based on the concepts of these solutions, Tian et al. later proposed a tolerance-control solution in [13].

Definition 1

(see [2] and [13]). A vector \(x \in \mathbb {R}^n\) is called

  1. 1.

    a tolerance solution of \(\mathbf{A} x = \mathbf{b} \) if for each \(A \in \mathbf{A} \) there exists \(b \in \mathbf{b} \) such that \(Ax = b\),

  2. 2.

    a control solution of \(\mathbf{A} x = \mathbf{b} \) if for each \(b \in \mathbf{b} \) there exists \(A \in \mathbf{A} \) such that \(Ax = b\),

  3. 3.

    a tolerance-control solution of \(\mathbf{A} x = \mathbf{b} \) if each row index of the system is either tolerance or control.

As we expand an interval linear system \({\varvec{{A}}}x = {\varvec{{b}}}\) to a two-sided interval linear system \({\varvec{{A}}}x = {\varvec{{B}}}y\), the types of solutions of \({\varvec{{A}}}x = {\varvec{{B}}}y\) presented in the following definition are developed in similar fashion as the solution concepts in \({\varvec{{A}}}x = {\varvec{{b}}}\).

Definition 2

A vector \((x,y) \in \mathbb {R}^n \times \mathbb {R}^p\) is called

  1. 1.

    a tolerance solution of \(\mathbf{A} x = \mathbf{B} y\) if for each \(A \in \mathbf{A} \) there exists \(B \in \mathbf{B} \) such that \(Ax = By\),

  2. 2.

    a control solution of \(\mathbf{A} x = \mathbf{B} y\) if for each \(B \in \mathbf{B} \) there exists \(A \in \mathbf{A} \) such that \(Ax = By\),

  3. 3.

    a tolerance-control solution of \(\mathbf{A} x =\mathbf{B} y\) if each row index of the system is either tolerance or control.

Without semantics, the mathematical expression of tolerance and control solutions are the same. In Sect. 3, we will mention more about these two solutions and separately redefine them according to their semantics.

We now consecutively establish Theorems 1–3 based on Definition 2 to find necessary and sufficient conditions for checking tolerance and tolerance-control solvabilities of \(\mathbf{A} x = \mathbf{B} y\). The conditions presented in Theorems 2 and 3 are in a form of inequalities depending on center and radius of the coefficient interval matrices \({\varvec{A}}\) and \({\varvec{B}}\) with absolute terms |x| and |y|.

Theorem 1

A vector (x, y) is a tolerance solution of \(\mathbf{A} x = \mathbf{B} y\) if and only if it satisfies \(\mathbf{A} x \subseteq \mathbf{B} y\).

Proof

Assume that (x, y) is a tolerance solution of \({\varvec{{A}}}x = {\varvec{{B}}}y\). Let \(A \in {\varvec{{A}}}\). Then, there exists \(B \in {\varvec{{B}}}\) such that \(Ax = By\). Thus,

$$ Ax = By \in {\varvec{{B}}}y = \left[ \underline{{\varvec{B}}y} , \overline{{\varvec{B}}y}\right] , $$

that is,

$$ \underline{{\varvec{B}}y} \le Ax \le \overline{{\varvec{B}}y} \;\; \text {for any}\;A \in {\varvec{{A}}}, $$

which concludes \({\varvec{{A}}}x \subseteq {\varvec{{B}}}y\). Conversely, we suppose that (x, y) satisfies \({\varvec{{A}}}x \subseteq {\varvec{{B}}}y\). Then, \(Ax \in {\varvec{{B}}}y\) for all \(A \in {\varvec{{A}}}\). Therefore, \(Ax = By\) for all \(A \in {\varvec{{A}}}\) and for some \(B \in {\varvec{{B}}}\). Hence, (x, y) is a tolerance solution.   \(\square \)

Theorem 2

A vector (x, y) is a tolerance solution of \(\mathbf{A} x = \mathbf{B} y\) if and only if it satisfies

$$\begin{aligned} | A_cx-B_cy | \le \varDelta _B|y| -\varDelta _A |x|. \end{aligned}$$
(7)

Proof

Let (x, y) be a tolerance solution of \({\varvec{{A}}}x = {\varvec{{B}}}y\). By Theorem 1 and (2),

$$ \left[ A_c x -\varDelta _A|x|, A_c x+ \varDelta _A |x| \,\right] = {\varvec{{A}}}x \subseteq {\varvec{{B}}}y = \left[ B_c y-\varDelta _B|y|, B_c y+ \varDelta _B |y| \,\right] . $$

Thus,

$$ B_c y-\varDelta _B|y| \le A_c x -\varDelta _A|x| \le A_c x+ \varDelta _A |x| \le B_c y+ \varDelta _B |y|, $$

which implies

$$\begin{aligned} -(\varDelta _B|y| -\varDelta _A|x|) \le A_c x - B_c y \le \varDelta _B |y|- \varDelta _A |x|. \end{aligned}$$
(8)

Conversely, let (x, y) satisfy condition (7) Then, it gives (8), which means

$$ \underline{{\varvec{B}}y}=B_cy-\varDelta _B|y| \le A_cx -\varDelta _A |x| =\underline{{\varvec{A}}x} $$

and

$$ \overline{{\varvec{A}}x} =A_cx +\varDelta _A |x| \le B_cy+\varDelta _B|y| = \overline{{\varvec{B}}y}. $$

Therefore, \({\varvec{{A}}}x \subseteq {\varvec{{B}}}y\) and (x, y) becomes a tolerance solution.   \(\square \)

We can use inequality (7) to verify whether a given vector (x, y) is a tolerance solution to our two-sided interval linear system. The system of inequality (7) has the absolute terms |x| and |y|, which means it is not the system of linear inequalities, in general. It depends on the signs of x and y components. However, when we consider the nonnegative domain of vector variables x and y, the inequality becomes a simple form as

$$ \varDelta _Ax-\varDelta _By \le A_cx-B_cy \le \varDelta _By -\varDelta _Ax, $$

which is obtained by substituting \(|x|=x\) and \(|y|=y\). This turns into

$$\begin{aligned} (B_c-\varDelta _B)y \le (A_c-\varDelta _A)x\;\;\text {and}\;\;(A_c+\varDelta _A)x \le (\varDelta _B+B_c)y. \end{aligned}$$
(9)

According to (1), the inequalities (9) can be concluded as the corollary below.

Corollary 1

Let x and y be nonnegative vector variables. A vector (x, y) is a tolerance solution of \(\mathbf{A} x = \mathbf{B} y\) if and only if it satisfies

$$ \underline{B}y\le \underline{A}x\;\;\text {and}\;\;\overline{A}x\le \overline{B}y. $$

The similar statements of Theorems 1–2 and Corollary 1 for a control solution can be done easily by interchanging the roles of “\({\varvec{{A}}}\) and \({\varvec{{B}}}\)” and “x and y”.

Theorem 3

A vector (x, y) is a tolerance-control solution of \(\mathbf{A} x = \mathbf{B} y\) if and only if it satisfies

$$\begin{aligned} | A_cx-B_cy | \le \varDelta _A|x|+\varDelta _B|y|-2\delta , \end{aligned}$$
(10)

where \(\delta \) is a vector in \(\mathbb {R}^m\) with the following components

$$ \delta _i= {\left\{ \begin{array}{ll} (\varDelta _A|x|)_i, &{}\text {if}\;\text {i}\in \text {P};\\ (\varDelta _B|y|)_i, &{}\text {if}\;\text {i}\in \text {M}\setminus \text {P}, \end{array}\right. } $$

and \(P=\{i\in M: (\varvec{A}x)_i \subseteq (\varvec{B}y)_i\}\), \(M =\{1,2,\dots , m\}\).

Proof

Assume that (x, y) is a tolerance-control solution of \(\varvec{A}x = \varvec{B}y\). Let P be a subset of M such that row \(i\in P\) of the system is tolerance. Then, the other \(i\in M\setminus P\) of the system is control. Using Theorem 2, we have

$$\begin{aligned} | (A_cx)_i-(B_cy)_i | \le (\varDelta _B|y|)_i -(\varDelta _A |x|)_i\;\;\text {for each }i\in P \end{aligned}$$
(11)

and

$$\begin{aligned} | (A_cx)_i-(B_cy)_i | \le (\varDelta _A |x|)_i-(\varDelta _B|y|)_i\;\;\text {for each }i\in M\setminus P \end{aligned}$$
(12)

By putting Inequalities (11) and (12) together,

$$\begin{aligned} |A_cx-B_cy|&\le \biggl (\varDelta _A|x|-2\sum _{i\in P} (\varDelta _A|x|)_ie_i\biggr )+ \biggl (\varDelta _B|y|-2\sum _{i\in M\setminus P} (\varDelta _B|y|)_ie_i\biggr )\\&=\varDelta _A|x|+\varDelta _B|y|-2 \biggl (\sum _{i\in P} (\varDelta _A|x|)_ie_i+ \sum _{i\in M\setminus P} \varDelta _B|y|)_ie_i\biggr )\\&=\varDelta _A|x|+\varDelta _B|y|-2\delta , \end{aligned}$$

where \(e_i\) is a m-column vector containing 1 at the \(i^{\text {th}}\) row and 0 elsewhere. Conversely, let (x, y) satisfy condition (10), which implies Inequalities (11) and (12). Therefore, (x, y) turns into a tolerance-control solution.   \(\square \)

3 Semantics of Tolerance and Control Solutions

Looking at the mathematical definitions in the previous section, it may seem that tolerance and control solutions are algebraically the same. So, why would we need to define them both? This is because one interval information could be more important than another. There are some missing details in Definition 2 about the priority of the interval information \({\varvec{{A}}}\) and \({\varvec{{B}}}\), which may not be represented clearly by just the mathematical quantification; “for all” and “for some”.

To be able to achieve a control solution of the system \({\varvec{{A}}}x = {\varvec{{B}}}y\) and justify the semantics of the word “control”, the boundary matrices \(\underline{A}\) and \(\overline{A}\) of \({\varvec{{A}}}\) must be more important than the ones of \({\varvec{{B}}}\). It could be the interval information that is given by an expert so that any quantity on the right must be controlled in the boundary of quantities on the left.

Similarly, to get the semantics of the word “tolerance” in a tolerance solution, the boundary matrices \(\underline{A}\) and \(\overline{A}\) of \({\varvec{{A}}}\) must be more important. They provide the range of left hand side quantities. Moreover, the situation to come up with a tolerance solution is such that we need every element in the range to be under the control of the range of the right hand side quantities. In other words, the left hand side quantities tolerate themselves within the range of the right hand side quantities.

For those reasons, we cannot simply substitute \({\varvec{{A}}}\) with \({\varvec{{B}}}\) and x with y, and infer that tolerance and control solutions are the same. Therefore, the priority of the information \({\varvec{{A}}}\) and \({\varvec{{B}}}\) need to be stated in their definitions as rewritten below.

Definition 3

Let an interval matrix \(\mathbf{A} \) play more important role to the two-sided interval system of linear equations \(\mathbf{A} x = \mathbf{B} y\). A vector \((x,y) \in \mathbb {R}^n \times \mathbb {R}^p\) is called

  1. 1.

    a tolerance solution of \(\mathbf{A} x = \mathbf{B} y\) if for each \(A \in \mathbf{A} \) there exists \(B \in \mathbf{B} \) such that \(Ax = By\). It is in the sense that the range of \(\mathbf{A} x\) tolerates within the range of \(\mathbf{B} y\),

  2. 2.

    a control solution of \(\mathbf{A} x = \mathbf{B} y\) if for each \(B \in \mathbf{B} \) there exists \(A \in \mathbf{A} \) such that \(Ax = By\). It is in the sense that the range of \(\mathbf{A} x\) controls the range of \(\mathbf{B} y\).

4 Applications on Tolerance and Control Solutions of a Two-Sided Interval Linear System

In this section, we illustrate two small examples to show the difference between tolerance and control solutions. These examples could be parts of any relevant application systems.

  • Problem Statement 1 is formulated as a tolerance solution to a two-sided interval linear system, which can be solved by system of inequalities.

  • Problem Statement 2 is formulated as a quadratic programming with control solutions to two-sided interval linear constraints, whose numerical example is demonstrated in Example 1.

Problem Statement 1

An animal food manufacturing company has its own quality control for its three formulas of chicken food: I, II, and III. These formulas must be checked for the level of carbohydrate, fiber, protein, and vitamins per kilogram per bag. The qualified bags must have the nutrients within the given boundaries as shown in the table below. The company also has a nutritionist who can advise customers about using these three formulas of chicken food for meat and egg chickens. To raise chickens for healthy meat and chickens for healthy eggs, those chickens should have nutrients within the range represented also in the table.

Type of nutrients

Interval amount of nutrient (kg)

Formula I

Formula II

Formula III

Meat chicken

Egg chicken

1. Carbohydrate

\(\left[ \underline{a}_{11}, \overline{a}_{11}\right] \)

\(\left[ \underline{a}_{12}, \overline{a}_{12}\right] \)

\(\left[ \underline{a}_{13}, \overline{a}_{13}\right] \)

\(\left[ \underline{b}_{11}, \overline{b}_{11}\right] \)

\(\left[ \underline{b}_{12}, \overline{b}_{12}\right] \)

2. Fiber

\(\left[ \underline{a}_{21}, \overline{a}_{21}\right] \)

\(\left[ \underline{a}_{22}, \overline{a}_{22}\right] \)

\(\left[ \underline{a}_{23}, \overline{a}_{23}\right] \)

\(\left[ \underline{b}_{21}, \overline{b}_{21}\right] \)

\(\left[ \underline{b}_{22}, \overline{b}_{22}\right] \)

3. Protein

\(\left[ \underline{a}_{31}, \overline{a}_{31}\right] \)

\(\left[ \underline{a}_{32}, \overline{a}_{32}\right] \)

\(\left[ \underline{a}_{33}, \overline{a}_{33}\right] \)

\(\left[ \underline{b}_{31}, \overline{b}_{31}\right] \)

\(\left[ \underline{b}_{32}, \overline{b}_{32}\right] \)

4. Vitamins

\(\left[ \underline{a}_{41}, \overline{a}_{41}\right] \)

\(\left[ \underline{a}_{42}, \overline{a}_{42}\right] \)

\(\left[ \underline{a}_{43}, \overline{a}_{43}\right] \)

\(\left[ \underline{b}_{41}, \overline{b}_{41}\right] \)

\(\left[ \underline{b}_{42}, \overline{b}_{42}\right] \)

The nutritionist suggests customers to mix three formulas together before feeding. The total amount of nutrients in the mixed chicken food must be within the range of the total amount of all needed nutrients to guarantee that all chickens provide healthy products. This relationship can be represented as a two-sided interval linear system (13)

$$\begin{aligned} \begin{pmatrix} \left[ \underline{a}_{11}, \overline{a}_{11}\right] &{} \left[ \underline{a}_{12}, \overline{a}_{12}\right] &{} \left[ \underline{a}_{13}, \overline{a}_{13}\right] \\ \left[ \underline{a}_{21}, \overline{a}_{21}\right] &{} \left[ \underline{a}_{22}, \overline{a}_{22}\right] &{} \left[ \underline{a}_{23}, \overline{a}_{23}\right] \\ \left[ \underline{a}_{31}, \overline{a}_{31}\right] &{} \left[ \underline{a}_{32}, \overline{a}_{32}\right] &{} \left[ \underline{a}_{33}, \overline{a}_{33}\right] \\ \left[ \underline{a}_{41}, \overline{a}_{41}\right] &{} \left[ \underline{a}_{42}, \overline{a}_{42}\right] &{} \left[ \underline{a}_{43}, \overline{a}_{43}\right] \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}=\begin{pmatrix} \left[ \underline{b}_{11}, \overline{b}_{11}\right] &{} \left[ \underline{b}_{12}, \overline{b}_{12}\right] \\ \left[ \underline{b}_{21}, \overline{b}_{21}\right] &{} \left[ \underline{b}_{22}, \overline{b}_{22}\right] \\ \left[ \underline{b}_{31}, \overline{b}_{31}\right] &{} \left[ \underline{b}_{32}, \overline{b}_{32}\right] \\ \left[ \underline{b}_{41}, \overline{b}_{41}\right] &{} \left[ \underline{b}_{42}, \overline{b}_{42}\right] \end{pmatrix}\begin{pmatrix} y_1\\ y_2 \end{pmatrix}, \end{aligned}$$
(13)
figure a

From the company’s point of view, it is important to control the nutrients in each formula of chicken foods. It turns out that the set of solutions to System (13) is the set of tolerance solutions as the total of the nutrients created by the mixed food must be within the range of healthy nutrients. On the other hand, when considering the customer’s side, the interval information about the nutrients needed for each chicken is the priority for the customer. In this case, the customer must control the nutrients in the mixed food by the range of the total amount of all needed nutrients for healthy chicken meat and eggs. Then, the set of solutions to System (13) can also be viewed as the tolerance solution set. Obviously, vector variables \(x=(x_1,x_2,x_3)^T\) and \(y=(y_1,y_2)^T\) are nonnegative. From Corollary 1, the tolerance solution (x, y) is obtained by solving the system of inequalities as follows:

$$ \underline{b}_{i1}y_1+\underline{b}_{i2}y_2-\underline{a}_{i1}x_1-\underline{a}_{i2}x_2-\underline{a}_{i3}x_3 \le 0 $$

and

$$ \overline{a}_{i1}x_1+\overline{a}_{2}x_2+\overline{a}_{i3}x_3-\overline{b}_{i1}y_1-\overline{b}_{i2}y_2 \le 0, $$

for each \(i\in \{1,2,3,4\}\).   \(\square \)

Problem Statement 2

A famous family bakery shop sells homemade fruit cakes and fruit tarts. The owner uses three grades of mixed dried berries: A, B, and C, by mixing them together to get the best dessert according to the family recipe. Suppose the owner determines the initial amount of fruit cakes and fruit tarts he/she wanted to make as \(\alpha _1\) and \(\alpha _2\), respectively, and sets up the initial amount of mixed dried berries grades A, B and C that he/she aims to buy as \(\beta _1, \beta _2\) and \(\beta _3\), respectively. One kilogram of each mixed dried fruit grade contains dried blueberries, dried cranberries, dried raspberries, and dried strawberries in the different uncertain quantities. The table below provides the interval quantities per kilogram of each mixed dried berries grade.

Type of dried berries

Interval amount of berry (kg)

Grade A

Grade B

Grade C

1. Blueberries

\(\left[ \underline{b}_{11}, \overline{b}_{11}\right] \)

\(\left[ \underline{b}_{12}, \overline{b}_{12}\right] \)

\(\left[ \underline{b}_{13}, \overline{b}_{13}\right] \)

2. Cranberries

\(\left[ \underline{b}_{21}, \overline{b}_{21}\right] \)

\(\left[ \underline{b}_{22}, \overline{b}_{22}\right] \)

\(\left[ \underline{b}_{23}, \overline{b}_{23}\right] \)

3. Raspberries

\(\left[ \underline{b}_{31}, \overline{b}_{31}\right] \)

\(\left[ \underline{b}_{32}, \overline{b}_{32}\right] \)

\(\left[ \underline{b}_{33}, \overline{b}_{33}\right] \)

4. Strawberries

\(\left[ \underline{b}_{41}, \overline{b}_{41}\right] \)

\(\left[ \underline{b}_{42}, \overline{b}_{42}\right] \)

\(\left[ \underline{b}_{43}, \overline{b}_{43}\right] \)

To control the quality of the desserts, the recipe says that the dessert must contain each type of dried berries in a certain level as shown in the following table.

Type of dried berries

Interval amount of berry (kg)

Fruit cake

Fruit tart

1. Blueberries

\(\left[ \underline{a}_{11}, \overline{a}_{11}\right] \)

\(\left[ \underline{a}_{12}, \overline{a}_{12}\right] \)

2. Cranberries

\(\left[ \underline{a}_{21}, \overline{a}_{21}\right] \)

\(\left[ \underline{a}_{22}, \overline{a}_{22}\right] \)

3. Raspberries

\(\left[ \underline{a}_{31}, \overline{a}_{31}\right] \)

\(\left[ \underline{a}_{32}, \overline{a}_{32}\right] \)

4. Strawberries

\(\left[ \underline{a}_{41}, \overline{a}_{41}\right] \)

\(\left[ \underline{a}_{42}, \overline{a}_{42}\right] \)

The relationship of how many kilograms of the mixed dried berries grades A, B, and C that the shop should have and how many fruit cakes and fruit tarts that the shop should make to guarantee the overall quality of the dessert becomes a two-sided interval linear system as follows:

$$\begin{aligned} \begin{pmatrix} \left[ \underline{a}_{11}, \overline{a}_{11}\right] &{} \left[ \underline{a}_{12}, \overline{a}_{12}\right] \\ \left[ \underline{a}_{21}, \overline{a}_{21}\right] &{} \left[ \underline{a}_{22}, \overline{a}_{22}\right] \\ \left[ \underline{a}_{31}, \overline{a}_{31}\right] &{} \left[ \underline{a}_{32}, \overline{a}_{32}\right] \\ \left[ \underline{a}_{41}, \overline{a}_{41}\right] &{} \left[ \underline{a}_{42}, \overline{a}_{42}\right] \end{pmatrix}\begin{pmatrix} x_1\\ x_2 \end{pmatrix}=\begin{pmatrix} \left[ \underline{b}_{11}, \overline{b}_{11}\right] &{} \left[ \underline{b}_{12}, \overline{b}_{12}\right] &{} \left[ \underline{b}_{13}, \overline{b}_{13}\right] \\ \left[ \underline{b}_{21}, \overline{b}_{21}\right] &{} \left[ \underline{b}_{22}, \overline{b}_{22}\right] &{} \left[ \underline{b}_{23}, \overline{b}_{23}\right] \\ \left[ \underline{b}_{31}, \overline{b}_{31}\right] &{} \left[ \underline{b}_{32}, \overline{b}_{32}\right] &{} \left[ \underline{b}_{33}, \overline{b}_{33}\right] \\ \left[ \underline{b}_{41}, \overline{b}_{41}\right] &{} \left[ \underline{b}_{42}, \overline{b}_{42}\right] &{} \left[ \underline{b}_{43}, \overline{b}_{43}\right] \end{pmatrix}\begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}, \end{aligned}$$
(14)
figure b

The quality of desserts is very important to the bakery shop. The owner wants to re-evaluate the amount \(x_1, x_2\) and \(y_1, y_2, y_3\) to make sure that the mixed dried berries the shop has would be covered by the range of the total amount of the mixed fruits in all dessert items. This way the shop would be able to guarantee the quality of the desserts. The set of solutions satisfies System (14) is considered to be the control solution set. In a situation when the owner wants the amount \(x_1, x_2\) and \(y_1, y_2, y_3\) as close as possible to the given values \(\alpha _1, \alpha _2\) and \(\beta _1, \beta _2, \beta _3\), respectively, it is the same as to minimize the function below:

$$\begin{aligned} \Vert (x,y)^T-(\alpha , \beta )^T\Vert ^2&= \sum _{j=1}^2 (x_j-\alpha _j)^2+\sum _{k=1}^3 (y_k-\beta _k)^2 \nonumber \\&= \sum _{j=1}^2 (x_j^2-2\alpha _jx_j+\alpha _j^2)+\sum _{k=1}^3 (y_k^2-2\beta _ky_k+\beta _k^2). \end{aligned}$$
(15)

It is sufficient to remove the constant terms \(\alpha _j^2\) and \(\beta _k^2\) from Eq. (15) for every \(j\in \{1,2\}\) and \(k\in \{1,2,3\}\). Therefore, we can model this problem as a quadratic program \(P_1\) with a two-sided interval linear constraint (14), whose constraints are obtained by using the statement of Corollary 1 for a control solution in the following way:

$$\begin{aligned} P_1:\;\;&\text {minimize}\;\;f(x,y)= \sum _{j=1}^2 (x_j^2-2\alpha _jx_j)+\sum _{k=1}^3 (y_k^2-2\beta _ky_k)\\&\text {subject to}\;\;\begin{aligned} \sum _{j=1}^2 \underline{a}_{ij}x_j-\sum _{k=1}^3 \underline{b}_{ik}y_k&\le 0,&\;\;&\forall i\in \{1,2,3,4\}\\ -\sum _{j=1}^2 \overline{a}_{ij}x_j+\sum _{k=1}^3 \overline{b}_{ik}y_k&\le 0,&\;\;&\forall i\in \{1,2,3,4\}\\ x_j, y_k&\ge 0.&\;\;&\forall j\in \{1,2\}\;\forall k\in \{1,2,3\} \end{aligned} \end{aligned}$$

The Lagrangian function for Problem \(P_1\) can be written by

$$\begin{aligned} L(z,\mu )=c^Tz+\frac{1}{2}z^TQz+\mu (A'z-b'), \end{aligned}$$
(16)

where

$$ c=\begin{pmatrix} -2\alpha _1 \\ -2\alpha _2 \\ -2\beta _1 \\ -2\beta _2 \\ -2\beta _3 \end{pmatrix},\;\;Q=\begin{pmatrix} 2&{}0&{}0&{}0&{}0 \\ 0&{}2&{}0&{}0&{}0 \\ 0&{}0&{}2&{}0&{}0 \\ 0&{}0&{}0&{}2&{}0 \\ 0&{}0&{}0&{}0&{}2 \end{pmatrix},\;\;z=\begin{pmatrix} x_1\\ x_2\\ y_1\\ y_2\\ y_3 \end{pmatrix} $$

and

$$ A'=\begin{pmatrix} \underline{a}_{11} &{}\underline{a}_{12} &{}-\underline{b}_{11}&{}-\underline{b}_{12}&{}-\underline{b}_{13} \\ \underline{a}_{21} &{}\underline{a}_{22} &{}-\underline{b}_{21}&{}-\underline{b}_{22}&{}-\underline{b}_{23} \\ \underline{a}_{31} &{}\underline{a}_{32} &{}-\underline{b}_{31}&{}-\underline{b}_{32}&{}-\underline{b}_{33} \\ \underline{a}_{41} &{}\underline{a}_{42} &{}-\underline{b}_{41}&{}-\underline{b}_{42}&{}-\underline{b}_{43} \\ -\overline{a}_{11}&{}-\overline{a}_{12} &{}\overline{b}_{11}&{} \overline{b}_{12}&{} \overline{b}_{13} \\ -\overline{a}_{21}&{}-\overline{a}_{22}&{} \overline{b}_{21}&{} \overline{b}_{22}&{} \overline{b}_{23} \\ -\overline{a}_{31}&{}-\overline{a}_{32} &{}\overline{b}_{31}&{} \overline{b}_{32}&{} \overline{b}_{33} \\ -\overline{a}_{41}&{}-\overline{a}_{42} &{}\overline{b}_{41}&{} \overline{b}_{42}&{} \overline{b}_{43} \end{pmatrix},\;\;b'=\begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{pmatrix} $$

and \(\mu =(\mu _1, \mu _2, \dots , \mu _8)\ge 0\) is the Lagrange multiplier with 5-dimensional row vector. Let u and v be surplus and slack variables to the inequalities

$$ c+Qz+(A')^T\mu ^T\ge 0\;\;\text {and}\;\; A'z-b'\le 0, $$

respectively. As shown in [5], we can represent (16) in the following linear constraints form:

$$\begin{aligned} Qz+(A')^T\mu ^T-u&= -c, \end{aligned}$$
(17)
$$\begin{aligned} A'z+v&= b', \end{aligned}$$
(18)
$$\begin{aligned} z\ge 0, \;\;\mu \ge 0,\;\; u\ge 0, \;\;v&\ge 0, \end{aligned}$$
(19)
$$\begin{aligned} u^Tz =0,\;\; \mu v&=0, \end{aligned}$$
(20)

where the equations shown in (20) prescribe complementary slackness. Since it can clearly be seen that the matrix Q is positive definite, the conditions (17)–(20) are necessary and sufficient for a global optimum. To create the appropriate linear program, we add thirteen artificial variables \(a_1, a_2, \dots , a_{13}\) to each constraint of (17) and (18) together with minimizing their sum, that is,

figure c

where \(a'=(a_1, a_2, \dots , a_5)^T\) and \(a''=(a_6, a_7, \dots , a_{13})^T\). Hence, the optimal solution to the quadratic program \(P_1\) is found out by solving the linear program \(P_2\).   \(\square \)

Example 1

According to Problem statement 2, we provide the numerical information in the following table.

Type of dried berries

Interval amount of berry (kg)

Fruit cake

Fruit tart

 Grade A

  Grade B

Grade C

1. Blueberries

[0.25, 0.32]

[0.20, 0.41]

[0.15, 0.30]

[0.60, 0.70]

[0.22, 0.25]

2. Cranberries

[0.05, 0.18]

[0.26, 0.35]

[0.20, 0.20]

[0.23, 0.35]

[0.08, 0.12]

3. Raspberries

[0.03, 0.15]

[0.24, 0.64]

[0.10, 0.16]

[0.04, 0.10]

[0.45, 0.55]

4. Strawberries

[0.04, 0.36]

[0.34, 0.45]

[0.32, 0.48]

[0.14, 0.28]

[0.18, 0.20]

  • The initial amount of fruit cakes and fruit tarts is \(\alpha _1=16\) and \(\alpha _2=24\), respectively.

  • The initial amount of mixed dried berries grade A, B and C is \(\beta _1=15, \beta _2=12\) and \(\beta _3=10\), respectively.

As explained in Problem statement 2 with the above information, our problem can be represented by Problem \(P_2\), that is,

$$ \text {minimize}\;\;a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8+a_9+a_{10}+a_{11}+a_{12}+a_{13} $$

subject to

$$\begin{aligned} 2x_1+0.25\mu _1+0.05\mu _2+0.03\mu _3+0.04\mu _4 -0.32\mu _5 -0.18\mu _6 -0.15\mu _7 -0.36\mu _8-u_1+a_1&= 32, \\ 2x_2+0.20\mu _1 +0.26\mu _2+ 0.24\mu _3+ 0.34\mu _4 -0.41\mu _5 -0.35\mu _6 -0.64\mu _7 -0.45\mu _8-u_2+a_2&= 48, \\ 2y_1-0.15\mu _1 -0.20\mu _2 -0.10\mu _3 -0.32\mu _4+ 0.30\mu _5+ 0.20\mu _6+ 0.16\mu _7+ 0.48\mu _8-u_3+a_3&= 30, \\ 2y_2-0.60\mu _1 -0.23\mu _2 -0.04\mu _3 -0.14\mu _4+ 0.70\mu _5+ 0.35\mu _6+ 0.10\mu _7+ 0.28\mu _8-u_4+a_4&= 24, \\ 2y_3-0.22\mu _1 -0.08\mu _2 -0.45\mu _3 -0.18\mu _4+ 0.25\mu _5+ 0.12\mu _6+ 0.55\mu _7+ 0.20\mu _8-u_5+a_5&= 20, \\ 0.25x_1+0.20x_2 -0.15y_1 -0.60y_2 -0.22y_3+v_1+a_6&= 0, \\ 0.05x_1+0.26x_2 -0.20y_1- 0.23y_2 -0.08y_3+v_2+a_7&= 0, \\ 0.03x_1+0.24x_2 -0.10y_1 -0.04y_2 -0.45y_3+v_3+a_8&= 0, \\ 0.04x_1+0.34x_2 -0.32y_1 -0.14y_2 -0.18y_3+v_4+a_9&= 0, \\ -0.32x_1 -0.41x_2+0.30y_1+0.70y_2+0.25y_3 +v_5+a_{10}&= 0, \\ -0.18x_1 -0.35x_2+0.20y_1+0.35y_2+0.12y_3 +v_6+a_{11}&= 0, \\ -0.15x_1 -0.64x_2+0.16y_1+0.10y_2+0.55y_3 +v_7+a_{12}&= 0, \\ -0.36x_1 -0.45x_2+0.48y_1+0.28y_2+0.20y_3 +v_8+a_{13}&= 0, \end{aligned}$$

where all variables are nonnegative and complementary conditions are satisfied. By applying the simplex method, the optimal solution to this problem is eventually displayed as

figure d

In this section we have presented two particular situations to show the difference between tolerance and control solutions together with the processes for solving them. The tolerance solution as Problem Statement 1 can directly be accomplished using system of inequalities. The quadratic programming problem constrained with control solutions as Problem Statement 2 was transformed to become an appropriate linear program. Then, the simplex method enables us to obtain the optimal solution of the problem as displayed in the above example.

5 Conclusion

This paper presents the concepts of tolerance and control solutions of a two-sided interval linear system together with their semantics to the system \({\varvec{A}}x={\varvec{B}}y\). The conditions to verify that (x, y) is a tolerance or a control or a tolerance-control solution are also achieved in Theorems 1–3. In application problems, the vectors x and y are normally specified by nonnegative variables. Therefore, we simplify Theorem 2 to be Corollary 1 and applied it to implement a two-sided interval linear system and a quadratic programming with two-sided interval linear constraints. This work should be beneficial to any applications that have the restrictions in the format of two-sided interval linear system.