Keywords

1 Introduction

Smartphone devices are equipped with multiple sensors that can record user behavior on the handsets. With the help of large-scale smartphone usage data, researchers are able to study human behavior in the real world. Since location information is one of the crucial aspects of human behaviors, investigating human mobility from mining mobile data has drawn the attentions of many researchers.

Previous research in this filed mainly focused on discovering the significant places or predicting the transition among the significant places [2, 6, 11]. However, these research neglected the data sampled at the places where one stays for a relatively short time period, for instance, amid the transitions. As opposed to this point of view, we suggest that these type of data is important for revealing human mobility patterns as well. In our work, the human mobility is recorded by the GPS modules embedded on the smartphone devices. It should be emphasized that GPS data (longitudes and latitudes) are not evenly distributed spatially because one may stay longer at the significant places (i.e., a home or school) than at the less significant places (i.e., a restaurants or road). Thus, an appropriate description for human mobility is to treat the location of an individual as a set of data points randomly distributed in the space with respect to different probabilities. Moreover, in practice, the data collecting procedure may not be continuous all the time because the GPS module is turned off or does not function well sometimes. As a consequence, it arises the issue of data sparsity. These unique data characteristics prevent researchers adopting some conventional methods. Therefore, in our work, we adopt a probabilistic approach to describe the daily human mobility. As compared to conventional methods, we believe our approach can explore more information from the original GPS data and mitigate the impact of data sparsity.

The first step of the method is to estimate the probability density for each day’s trajectories. For such a task, Gaussian Mixture Model [14] is a possible solution. However, the standard Gaussian Mixture Model needs to set the number of components in advance, which is tricky to implement because the trajectory data can be statistically heterogeneous and a fixed component number for all the daily trajectories is not appropriate either. To handle this problem, we adopt the Infinite Gaussian Mixture Model (IGMM) [13], in which the Dirichlet process prior is used to modify the mixed weights of components. Further, to measure the difference between different mobility probability densities, the Kullback-Leibler (KL) divergence [9] is used. The KL divergence is an asymmetric metric, which means the distance from distribution p to distribution q is not the same as the distance from distribution q to distribution p unless they are identical. We exploit the inequality property of the KL divergence to reveal the subordinate relationship of one trajectory to another. Finally, we devise a clustering algorithm using the IGMM with the KL divergence to discover the mobility patterns existing in human mobility data. More importantly, as compared to traditional methods, our clustering algorithm is automatic because it does not require a preset of the pattern number.

The reminder of the paper is organized as follows. Section 2 surveys the related work. Section 3 addresses the problem we are tackling in this paper. In Sect. 4, the proposed method is depicted. In Sect. 5 presents the conducted experiment and its results to evaluate our method with real user data. Finally, we conclude our paper and discuss about the future work in Sect. 6.

2 Related Work

A widespread topic is to predict human mobility with the smartphone usage contextual information, e.g., temporal information, application usage, call logs, WiFi status, Cell ID, etc. In [2] for instance, the researchers applied various machine learning techniques to accomplish prediction tasks such as the next-time slot location prediction and the next-place prediction. In particular, they exploited how different combinations of contextual features are related to smartphone usage can affect the prediction accuracy. Moreover, they also compared the predicting performances of the individual models and the generic models.

Another frequently-used method for such tasks is to use probabilistic models. By calculating the conditional probabilities between contextual features, [5] developed the contextual conditional models for the next-place prediction and visit duration prediction. In [4], the researchers presented the probabilistic prediction frameworks based on Kernel Density Estimation (KDE). [4] utilized conditional kernels density estimation to predict the mobility events while [12] devised different kernels for different context information types. In [11], the authors developed a location Hierarchical Dirichlet Process (HDP) based approach to model heterogeneous location habits under data sparsity.

Among the other possible approaches, [18] proposed a Hypertext Induced Topic Search based inference model for mining interesting locations and travel sequences using a large GPS dataset in a certain region. In [6], the authors employed the random forests classifiers to label different places without any geo-location information. [15] made use of nonlinear time series analysis of the arrival time and residence time for location prediction.

In particular, for clustering user trajectories, there exists several different methods. However, these conventional algorithms are not applicable to our objectives. For example, some researchers used K-means [1] in their work, whereas K-means can not handle the trajectories with complex shapes or noisy data because it is based on Euclidean distance. Besides, it also needs the pre-knowledge of the cluster numbers, which is not acquirable in many real-world cases. DBSCAN [17], a density-based clustering techniques, can deal with data with arbitrary shapes and does not require the number of cluster in advance. However, it still needs to set the minimum points number and neighbourhood radius to recognize the core areas and it treats the non-core data points as noise. As for the grid searching algorithm [5], it focus on detecting the stay points within a set of square regions, whereas it fails to reveal the mobility at a larger scale.

3 Problem Formulation

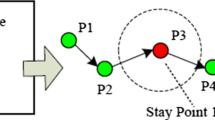
In this paper, our purpose is to discover the mobility patterns for each individual from the GPS location data. As shown in Fig. 1a, the mobility for one individual consists of many different trajectories (the data is from the MDC dataset, the detailed data description will be in following experiments). A trajectory here means that a set of GPS data points collected from the user’s smartphone, however, we do not treat it as a sequence. We believe that one’s daily mobility is rather regular and there are common mobility patterns shared among different daily trajectories. Generally, one may follow the regular daily itineraries, for instance, home-work place/school-home. Yet, on different days the daily itineraries may not be the same, for instance, on the way to home, one may take a detour to do shopping in a supermarket sometimes. Hence, our objective is to discover all the potential daily mobility from the data with location information.

Fig. 1.
figure 1

GPS data samples.

Full size image

We extract each day’s trajectory from the all GPS trajectories from a user. Figure 1b reveals that daily trajectories recorded by GPS data are not distributed evenly in space. It may be caused by the data collecting procedure: some data collecting time period is actually relatively short (less than 24 h, in fact, only few hours sometimes), which leads to the data sparsity problem. In order to overcome this problem and exploit as much information as possible from the GPS data, we argue that a reasonable way to describe the daily trajectories is to estimate the probability density of the location data. The relationship among the trajectories can be represented by their probability densities. As a result, we can discover all the mobility patterns for each user. The tasks in this paper will be as follows:

  • Task 1: to estimate the probability density for mobility for each day.

  • Task 2: to measure the closeness between different trajectories.

  • Task 3: to discover the similar mobility patterns.

  • Task 4: to compare the proposed algorithm with other methods.

4 Proposed Method

4.1 Estimating Daily Trajectories Probability Density

We assume that the GPS location data points are distributed randomly spatially. The distribution of each day also consists of unknown number of heterogeneous sub-distributions. Therefore, one feasible method is to use mixed Gaussian models for estimating the probability density of daily mobility.

Gaussian Mixture Model. A Gaussian Mixture Model (GMM) is composed of a fixed number K of sub-components. The probability distribution of a GMM can be described as follows:

$$\begin{aligned} P(x)=\sum _{k=1}^{K}{\pi _k P(x | \theta _k)} \end{aligned}$$
(1)

where, x is the observable variable, \(\pi _k\) is the assignment probability for each model, with \(\sum _{k=1}^{K}\pi _k=1, (0<\pi _k<1)\), and \(\theta _k\) is the internal parameters of the base distribution.

Let \(z_n\) be the latent variables for indicating categories.

$$\begin{aligned} z_n \sim Categorical(z_n | \pi ) \quad \sum _{k=1}^{K}z_{nk}=1 \end{aligned}$$
(2)

where, \(z_n=[z_{n1}, z_{n2}, ..., z_{nk}, ..., z_{nK}]\), in which only one element \(z_{nk} = 1\). It means \(x_n\) is correspondent to \(\theta _k\).

If the base distribution is a Gaussian, then:

$$\begin{aligned} P(x | \theta _k)= N(x | \mu _k,\varLambda ^{-1}_k) \end{aligned}$$
(3)

where, \(\mu _k\) is the mean vector and \(\varLambda _k\) is the precision matrix.

Therefore, an observable sample \(x_n\) is drawn from GMM according to:

$$\begin{aligned} \ x_n \sim \prod _{k=1}^{K}{{N(x_n | \nu _k,\varLambda _k)}^{z_{nk}}} \end{aligned}$$
(4)

As it is illustrated above, one crucial issue of GMM is to pre-define the number of components K. It is tricky because the probability distribution for each day’s mobility is not identical. Thus, to define a fixed K for all mobility GMM models is not suitable in our case.

Infinite Gaussian Mixture Model.Alternatively, we resort to the Infinite Gaussian Mixture Model (IGMM) [13]. As compared to the finite Gaussian Mixture Model, by using a Dirichlet process (DP) prior, IGMM does not need to specify the number of components in advance. Figure 2 presents the graphical structure of the Infinite Gaussian Mixture Model.

Fig. 2.
figure 2

The plate representation of Infinite Gaussian Mixture Model.

Full size image

In Fig. 2, the nodes represent the random variables and especially, the shaded node is observable and the unshaded nodes are unobservable. The edges represent the conditional dependencies between variables. The variables within the plates means that they are drawn repeatedly.

According to Fig. 2, the Dirichlet process can be depicted as:

$$\begin{aligned} G \sim DP(\alpha , G_0) \end{aligned}$$
(5)

where, G is a random measure, which consists of infinite base measures \(G_0\) and \(\lambda \) is the hyper-parameter of \(G_0\). In our case, it is a series of Gaussian distributions. And \(\alpha \sim Gamma(1,1)\) is the concentration parameter. N is the total samples number. \(\theta _k\) is the parameters of base distribution. \(X_k\) is the observable data for \(\theta _k\). \(Z_k\) is the latent variables that indicates the category of \(X_k\).

Alternatively, G can be explicitly depicted as follow:

$$\begin{aligned} G(\theta ) = \sum _{k=1}^{\infty }\pi _k \delta _{\theta _k} \end{aligned}$$
(6)

where, \(\theta _k \sim G_0(\lambda )\), and \(\delta \) is Dirac function. \(\pi _k\) determines the proportion weights of the clusters and the \(\delta _{\theta _k}\) is the prior of the \(\theta _k\) to determine the location of clusters in space.

We choose the Stick-breaking process (SBP) [16] to implement the Dirichlet process as the prior of \(\pi _k\). The Stick-breaking process can be described as follow:

$$\begin{aligned} \pi _k = \nu _k\prod _{j=1}^{k-1}{(1-\nu _{j})} \quad k\ge 2 \end{aligned}$$
(7)

where, \(\nu _k \sim Beta(1,\alpha )\).

Since \(P(x|\theta )\) is Gaussian, \(\theta =\{\mu ,\varLambda \}\). Further, let \(G_0\) be a Gaussian-Wishart distribution, then, \(\mu _k, \varLambda _k \sim G_0(\mu , \varLambda )\). Therefore, similarly, drawing an observable sample \(x_n\) from IGMM can be described as follow:

$$\begin{aligned} \ x_n \sim \prod _{k=1}^{\infty }{{N(x_n|\nu _k,\varLambda ^{-1}_k)}^{z_{nk}}} \end{aligned}$$
(8)

Variational Inference (VI) is used to solve the IGMM models. In contrast with Gibbs sampling, a Markov chain Monte Carlo (MCMC) method, VI is relatively faster which makes it salable to large datasets [3]. The results will be demonstrated in the later experiments.

4.2 Measure Daily Trajectories Similarities

The Kullback-Leibler (KL) divergence is a metric to evaluate the closeness between two distributions. For continuous variables, the KL divergence \(D_{KL}(p||q)\) is the expectation of the logarithmic difference between the p and q with respect to probability p and vice versa. From (9) and (10), it can be seen that the KL divergence is non-negative and asymmetric. In many occasions, the inequality of the KL divergence is notorious. However, in our method, we take advantage of this characteristic of inequality to reveal the similarities among different trajectories instead of other symmetric metrics.

$$\begin{aligned} D_{KL}(p||q) = \int _{-\infty }^{\infty } p(x) \log (\frac{p(x)}{q(x)}) dx \end{aligned}$$
(9)
$$\begin{aligned} D_{KL}(q||p) = \int _{-\infty }^{\infty } q(y) \log (\frac{q(y)}{p(y)}) dy \end{aligned}$$
(10)

There is no closed form to implement the KL divergence by the definition of (9) and (10) for Gaussian Mixture Models. Therefore, we resort to the Monte Carlo simulation method proposed in [7]. Then, the KL divergence can be calculated via:

$$\begin{aligned} D_{KL_{MC}}(p||q) =\frac{1}{n} \sum _{i=1}^{n} \log (\frac{p(x_i)}{q(x_i)}) \end{aligned}$$
(11)
$$\begin{aligned} D_{KL_{MC}}(q||p) =\frac{1}{n} \sum _{i=1}^{n} \log (\frac{q(y_i)}{p(y_i)}) \end{aligned}$$
(12)

This method is to draw a large amount of i.i.d samples \(x_i\) from distribution p to calculate \(D_{KL_{MC}}(p||q)\) according to (11) and \(D_{KL_{MC}}(p||q) \rightarrow D_{KL}(p||q)\) as \(n \rightarrow \infty \). It is the same for implementing (10) by using (12). The results will be demonstrated in the later experiments. Furthermore, if we define a representative trajectory for a mobility pattern then we can distinguish whether a new trajectory belong to this cluster by comparing it to the most representative trajectory. To this end, we need to set a threshold with a lower bound and an upper bound for the KL divergences, afterwards it can be used as the metrics to cluster the trajectories.

4.3 Discovering Mobility Patterns

The proposed algorithm is shown in Algorithm 1 and its variables are described in Table 1. The first step of the clustering algorithm is to calculate the probability densities by using the Infinite Gaussian Mixture Models. At this step, we create a list, in which the members are the probability densities of each trajectories. Then the first cluster is created with one trajectory as its first member and it also will be the first baseline trajectories used to compare with other trajectories. It may be replaced by other trajectories later. Afterwards, we select another daily trajectory in the list and calculate the KL divergences, both \(D_{KL(p||q)}\) and \(D_{KL(q||p)}\). The new trajectory is added to the current cluster if the minimum and maximum of the KL-divergences are smaller than the lower threshold and the upper threshold of the thresholds respectively at the same time. If the \(D_{KL(p||q)}\) is smaller than \(D_{KL(q||p)}\), the new trajectory become the new baseline for the current cluster. This step will be repeated until all the trajectories belonging to the current cluster are discovered at the end of this iteration. Then all the members of the current cluster are removed from the iteration because we assume that each trajectory can only be the member of one mobility pattern. At the start of new iteration, a new cluster is created, the above steps will be repeated until the list is empty.

Table 1. Variables description
Full size table

As it can be seen that our algorithm is designed to discover the latent mobility patterns automatically without the pre-knowledge of the number of existing patterns.

5 Experiments and Results

5.1 Data Description

We use the Mobile Data Challenge (MDC) dataset [8, 10] to validate our method. This dataset records a comprehensive smartphone usage with fine granularity of time. The participants of the MDC dataset are up to nearly 200 and the data collection campaign lasted more than 18 months. This abundant information can be used to investigate individual mobility patterns in our research. We attempt to find the trajectories that belong to the same mobility patterns, therefor we focus on the spatial information of the GPS records, namely, the latitudes and longitudes, while the time-stamps of the data are not considered. In addition, the data we use is unlabeled and without any semantic information.

figure a
Fig. 3.
figure 3

Distribution estimation by GMM and IGMM (negative log-likelihood)

Full size image

5.2 Experimental Setup

For the experiments, we randomly select 20 users with sufficient data. Each user’s is segmented by the time range of one day. Generally, the data length of each day varies from less than 4 h to 24 h and most of them is less than 8 h.

5.3 Experimental Results

Probability Density Estimation. Fig. 3a and Fig. 3b show the density estimation results obtained by the GMM and the IGMM, respectively. It can be seen that, compared to the GMM, the result of the IGMM is less overfitting than the GMM. It suggests that the IGMM is not affected by the number of components and it infers more information from the original data and it is less influenced by data sparsity. That is to say, on the same dataset, the computational results of the IGMM have higher fidelity. Hence, in our approach, we chose the IGMM to estimate probability density of daily mobility.

Measuring Daily Trajectories Similarities. As shown in Fig. 4, we select 5 daily trajectories from the data of one random user to demonstrate the KL divergences between different trajectories. The baseline trajectory is Trajectory 1 and the rest of trajectories are chosen to make comparisons.

Table 2. KL-divergences for different trajectories.
Full size table
Fig. 4.
figure 4

Comparison between different trajectories.

Full size image

The combinations are shown in Fig. 4 and the results are illustrated in Table 2. Trajectory 2 is nearly a sub-part of Trajectory 1, the KL divergence values are both small, thus Trajectory 2 and Trajectory 1 can be regarded to belong to the same mobility pattern. Trajectory 3 is very similar to Trajectory 1 and \(D_{KL}(p||q)\) almost equals to \(D_{KL}(q||p)\). Hence, they also are the members of the same mobility pattern. Trajectory 4 shares a small part with Trajectory 1 whereas generally they are very different. \(D_{KL}(p||q)\) and \(D_{KL}(q||p)\) are both very large. Therefore, Trajectory 4 and Trajectory 1 are different patterns. For Trajectory 5 and Trajectory 1. \(D_{KL}(p||q)\) is small but \(D_{KL}(p||q)\) are very large. So they naturally are not in the same pattern. Finally, we can say that the Kl divergence can be used as the distance metrics to distinguish different trajectory patterns.

Discovering Daily Mobility Patterns. We run our algorithm on the data of the 20 users to discover their daily mobility patterns. The partial clustering results are demonstrated in Fig. 5. It proves our method is able to find different mobility patterns even under the condition of noise and discontinuity. Figure 6 shows that our approach is able not only to identify the different patterns in the daily trajectories data but also to find the most representative trajectories for each mobility pattern. Figure 7a shows the number of discovered mobility pattern for all the user in our experiments. Figure 7b depicts the number of members for each discovered mobility patterns for all users.

Fig. 5.
figure 5

Discovered mobility patterns from 3 random selected users. Different colors represents different days. (Color figure online)

Full size image

Comparing with Other Methods. In comparison with the IGMM-based model, we utilize Kernel Density Estimation (KDE) and a set of Gaussian Mixture Models with different numbers of components (GMM-n), to estimate the daily mobility probability densities in our proposed clustering algorithm. Since the GPS data are not labeled, which means that the ground truth is not available. In this case, we run our algorithm on all the trajectories collected from the 20 users and choose the mean log-likelihood, which indicts the reliability of the models, as a reasonable evaluation metrics. The results in Table 3 show that our method outperforms other conventional methods.

Fig. 6.
figure 6

Representative trajectories for each discovered mobility patterns.

Full size image
Fig. 7.
figure 7

Statistical analysis of discovered patterns.

Full size image
Table 3. Overall mean log-likelihood for different models
Full size table

6 Conclusion

In this work, we present a probabilistic approach to discover human daily mobility patterns based on GPS data collected by smartphones. In our approach, the human daily mobility is considered as sets of probability distributions. We argue that Infinite Gaussian Mixture Model is more appropriate than the standard Gaussian Mixture Model on this issue. Further, in order to find the similar trajectories, we use the Kullback-Leibler divergences as the distance metrics. Finally, we devise a novel automatic clustering algorithm combining the advantages of IGMM and the KL divergence so as to discover human daily mobility patterns. Our algorithm do not need the knowledge of the cluster number in advance. For validation, we conducted a set of experiments to prove the effectiveness of our method. For further study, we plan to use WiFi fingerprint data and other machine learning methods to study human mobility.